Wild Circuits Investigating the Limits of MINMAXAVG Circuits

Wild Circuits Investigating the Limits of MIN/MAX/AVG Circuits Brendan Juba Faculty Advisor: Manuel Blum Graduate Mentor: Ryan Williams

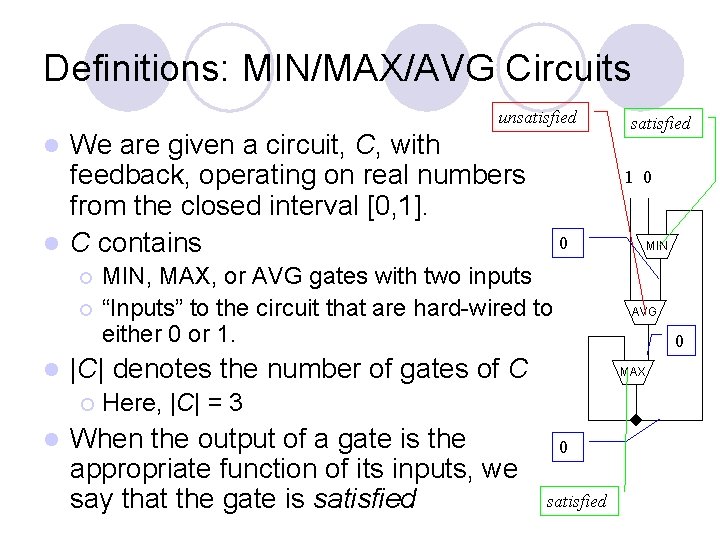
Definitions: MIN/MAX/AVG Circuits unsatisfied We are given a circuit, C, with feedback, operating on real numbers from the closed interval [0, 1]. l C contains satisfied l 1 0 0 MIN, MAX, or AVG gates with two inputs ¡ “Inputs” to the circuit that are hard-wired to either 0 or 1. MIN ¡ l 0 |C| denotes the number of gates of C ¡ l AVG MAX Here, |C| = 3 When the output of a gate is the appropriate function of its inputs, we say that the gate is satisfied 0 satisfied

Definitions: MIN/MAX/AVG Circuits l Settings of the gate outputs from the interval [0, 1] are value vectors ¡ ¡ l A value vector for C, v [0, 1]|C| The ith entry, vi, is the output of the ith gate. 1 0 MIN We may also consider an update function, F: [0, 1]|C| ¡ We are interested in two varieties: single-gate update functions and circuit-wide update functions: l A single gate update function replaces the output of a single designated gate with the correct output value. • We will call iterating over the single gate update functions “gate-by-gate update” l The circuit-wide update function simultaneously replaces the output of every gate with a value that is correct with respect to the old values AVG MAX

Definition: Stable Circuit Problem l A vector v is stable iff every gate is satisfied. (F(v) = v) ¡ l We wish to find these stable vectors. Gate-by-gate update from 0 clearly obtains a stable vector in the limit. This is the minimum stable solution stable 1 0 MIN 0 1/2 unstable 1 0 MIN 0 1/2 AVG MAX 1/2 0

Stable Circuit Decision Problem We designate some ith gate of C in the minimum stable solution, s, and ask, “is si ≥ 1/2? ” l We can reduce the function problem to this decision problem. We can find 2|C| bits of any si, which may be shown to be sufficient. l ¡ Suppose there is a gate xk: sxk ≥ 1/2 iff the kth bit of si is a 1 l l ¡ Depending on whether sxk ≥ 1/2, we add a new gate, xk+1: AVG(xk, 1/2 -1/22 k), if sxk =. 100… 0 AVG(xk, 1/2+1/22 k), if sxk =. 011… 1 l l ¡ If sxk ≥ 1/2, we assume its binary decimal representation is. 100… 0 with 0 s in positions 2 through 2 k-1 Otherwise, it is. 011… 1 with 1 s in positions 2 through 2 k-1 In the former case, sxk+1=(. 1)(. 100… 0 +. 011… 11) In the latter, sxk+1=(. 1)(. 011… 1 +. 100… 01) In the solution for the modified circuit, xk+1 clearly has the desired properties. The largest construction is O(|C|2) gates.

Unique Solution Circuits Replace any wire from x to y in the circuit with the construction on the right using m AVG gates l This circuit has a unique solution (Shapley, 1953) l ¡ ¡ ¡ l Suppose the original circuit-wide update function is F, stable solutions are u and v If ||u-v||∞= c, then it is easy to see c = ||u-v|| = (1 -1/2 m)||F(u)-F(v)|| ≤ (1 -1/2 m)c Clearly, c = 0. These solutions turn out to be arbitrarily close to the minimum stable solutions (for appropriate m). x 0 AVG AVG y

Stable Circuit is in NP co-NP (Condon, 1992) l A nondeterministic machine M can, in polynomial time, on input circuit C, for gate i ¡ ¡ Build a suitably close unique solution circuit C’ Guess the solution to C’ Verify the guessed vector is a solution Accept or reject, respectively, precisely when the value of gate i is above 1/2 (since C’ was close to C, either i is above 1/2 in neither, or it is above 1/2 in both)

Stable Circuit is P-hard If we use no AVG gates, the wires of the circuit will only carry 0 or 1 l It is immediate that we may use MIN as AND, MAX as OR l For any circuit with fixed inputs, we can construct a “complement” circuit l ¡ ¡ l Switch 0 inputs with 1 inputs Switch MIN gates with MAX gates We can now negate by crossing a wire between the original and complement circuits ¡ (In this AVG-free case, deciding the output is in P, too)

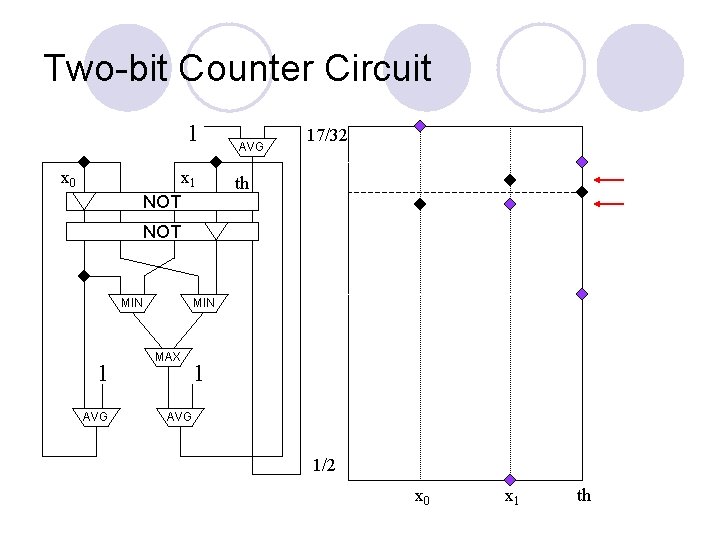
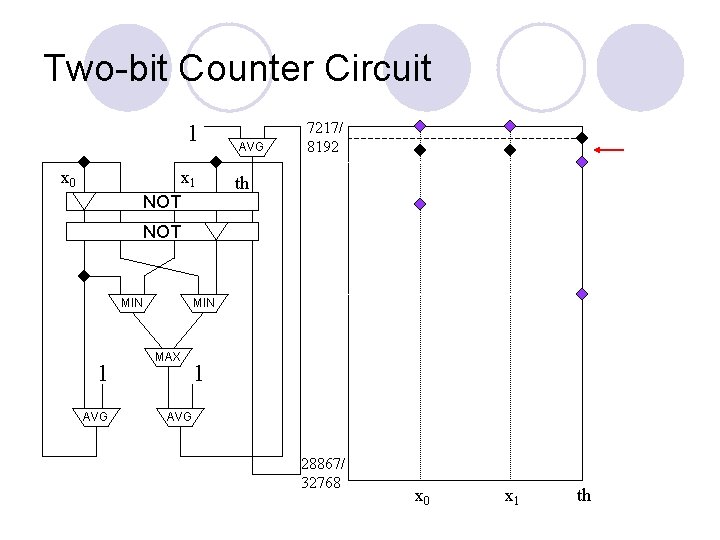
Observation and Motivation l If we apply gate-by-gate or circuit-wide update on arbitrary starting value vectors, we can obtain “interesting” circuits ¡ ¡ l One such “interesting” circuit is a binary counter We do not necessarily obtain the stable configurations of our circuits this way -- this is not Stable Circuit Can we obtain such circuits under gate-by-gate update from 0? ¡ If so, the minimum stable solution is the configuration of the device after an unbounded amount of time!

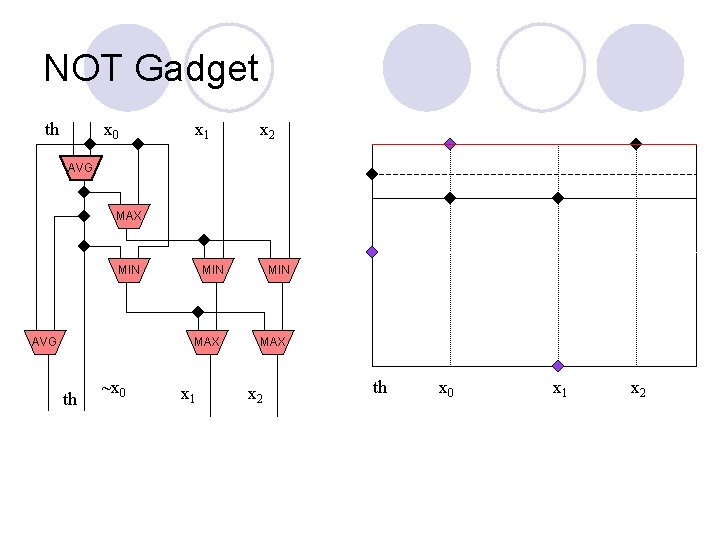
“Leapfrog” circuits l We assign each wire a “threshold” wire and interpret its value relative to that threshold ¡ ¡ Above threshold: T Below threshold: F It is already clear that we still have AND and OR l There is also a construction for NOT (next slide) l ¡ l If there are W wires which we wish to interpret relative to the same threshold, this gadget takes Θ(W) gates NB: The circuits are still monotone! ¡ ¡ As we update, a value may seem to rise or fall, as we follow it across different wires through the circuit The value on any particular wire only rises as the gates of the circuit are updated

NOT Gadget th x 0 x 1 x 2 AVG MAX MIN AVG MIN MAX th ~x 0 x 1 MIN MAX x 2 th x 0 x 1 x 2

Caveats l Assumptions: 1. 2. 3. l All values above [below] threshold are equal The values th, T, and F are all different We may specify the update order for the gates of the circuit Take each in turn: 1. 2. Everything starts from zero, the property is preserved by all three gates We can push th above zero by means of an AVG gate l 3. With feedback, we must pass the other wires to be interpreted relative to that threshold through similar constructions so as to maintain relative values Update order doesn’t change the solution we approach

Two-bit Counter Circuit 1 x 0 x 1 NOT AVG 1 th NOT MIN 1 AVG MIN MAX 1 AVG 0 x 1 th

Two-bit Counter Circuit 1 x 0 x 1 NOT AVG 17/32 th NOT MIN 1 AVG MIN MAX 1 AVG 1/2 x 0 x 1 th

Two-bit Counter Circuit 1 x 0 x 1 NOT AVG 781/ 1024 th NOT MIN 1 AVG MIN MAX 1 AVG 195/ 256 x 0 x 1 th

Two-bit Counter Circuit 1 x 0 x 1 NOT AVG 7217/ 8192 th NOT MIN 1 AVG MIN MAX 1 AVG 28867/ 32768 x 0 x 1 th

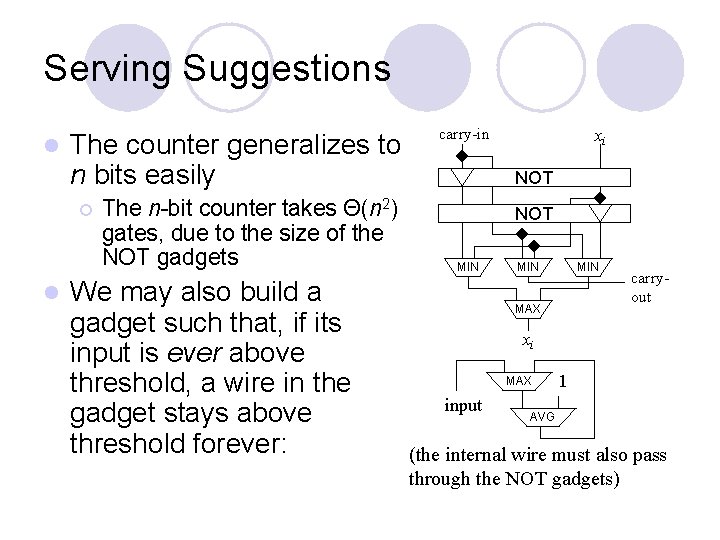
Serving Suggestions l The counter generalizes to n bits easily ¡ l The n-bit counter takes Θ(n 2) gates, due to the size of the NOT gadgets We may also build a gadget such that, if its input is ever above threshold, a wire in the gadget stays above threshold forever: carry-in xi NOT MIN MIN MAX carryout xi MAX input 1 AVG (the internal wire must also pass through the NOT gadgets)

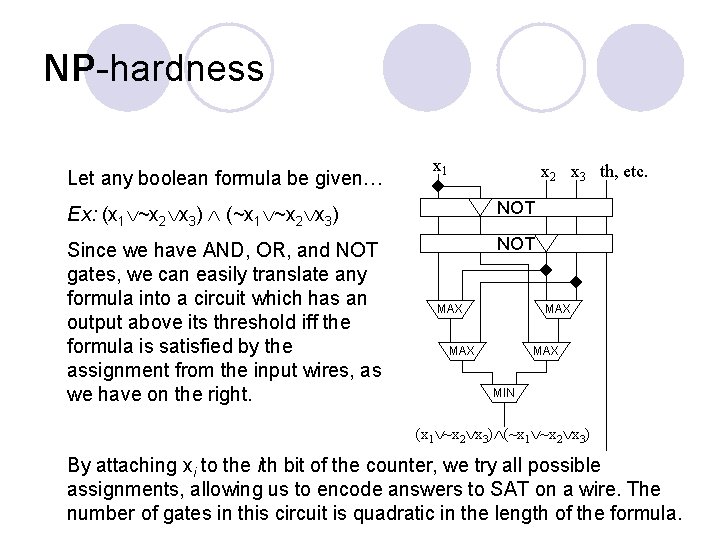
NP-hardness Let any boolean formula be given… x 1 x 2 x 3 th, etc. Ex: (x 1 ~x 2 x 3) (~x 1 ~x 2 x 3) NOT Since we have AND, OR, and NOT gates, we can easily translate any formula into a circuit which has an output above its threshold iff the formula is satisfied by the assignment from the input wires, as we have on the right. NOT MAX MAX MIN (x 1 ~x 2 x 3) (~x 1 ~x 2 x 3) By attaching xi to the ith bit of the counter, we try all possible assignments, allowing us to encode answers to SAT on a wire. The number of gates in this circuit is quadratic in the length of the formula.

Entering PSPACE We can still do better: using the counter, we will decide whether quantified boolean formulas are x 1 valid l Assume WLOG that the quantifiers alternate: odd variables are universal, even existential l Observe that the counter “walks” along the leaves x 0 of a tree of assignments, left to right. l Suppose that at the bottom we evaluate the quantifier-free part of the formula on the specified 00 01 10 assignment. l l Now suppose at every level of the tree, we have one bit of memory for the left branch ¡ l Pass T up the tree when ¡ ¡ l Set it to T when the branch is T, reset it to F when leaving that subtree. We see T at either branch at an level We see T at the right branch of a level with the left branch bit already set to T. T is passed up from the top of the tree iff we have a TQBF. 11

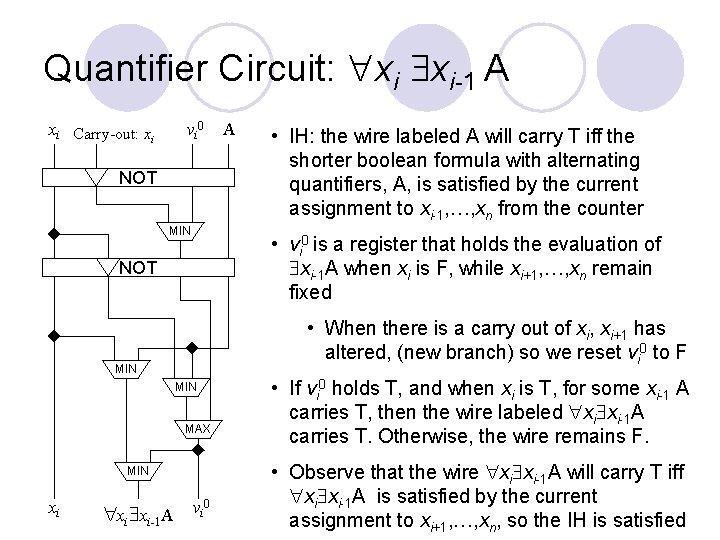
Quantifier Circuit: xi xi-1 A xi Carry-out: xi vi 0 NOT MIN • When there is a carry out of xi, xi+1 has altered, (new branch) so we reset vi 0 to F MIN MAX MIN xi xi-1 A • IH: the wire labeled A will carry T iff the shorter boolean formula with alternating quantifiers, A, is satisfied by the current assignment to xi-1, …, xn from the counter • vi 0 is a register that holds the evaluation of xi-1 A when xi is F, while xi+1, …, xn remain fixed NOT xi A vi 0 • If vi 0 holds T, and when xi is T, for some xi-1 A carries T, then the wire labeled xi xi-1 A carries T. Otherwise, the wire remains F. • Observe that the wire xi xi-1 A will carry T iff xi xi-1 A is satisfied by the current assignment to xi+1, …, xn, so the IH is satisfied

End of the Line: Thwarted by PSPACE l In the limit, the separation between T and F shrinks as the internal wires approach 1. ¡ It is not immediately clear how to recover the values of any wire from the minimum stable solution Recall: finding values in the limit (the minimum stable solution) is known to be in NP co-NP l Answers to PSPACE-hard problems (QSAT) may be encoded on the wires as we update l ¡ l Since the “space” in Leapfrog circuits is bounded by the number of gates, it is doubtful that such circuits can solve anything harder In the limit, it is impossible to distinguish the values in Leapfrog circuits unless NP = PSPACE

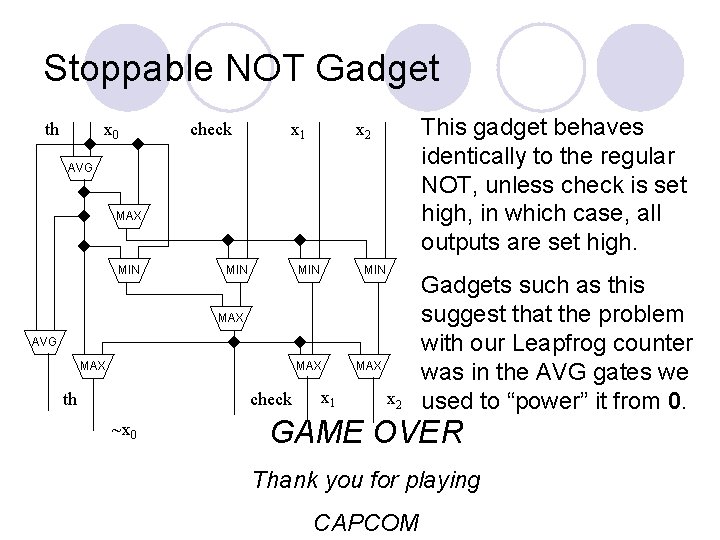
Stoppable NOT Gadget th x 0 check x 1 This gadget behaves identically to the regular NOT, unless check is set high, in which case, all outputs are set high. x 2 AVG MAX MIN MIN MAX AVG MAX th check ~x 0 x 1 MAX x 2 Gadgets such as this suggest that the problem with our Leapfrog counter was in the AVG gates we used to “power” it from 0. GAME OVER Thank you for playing CAPCOM