Wikipedia In mathematics a realvalued function f defined















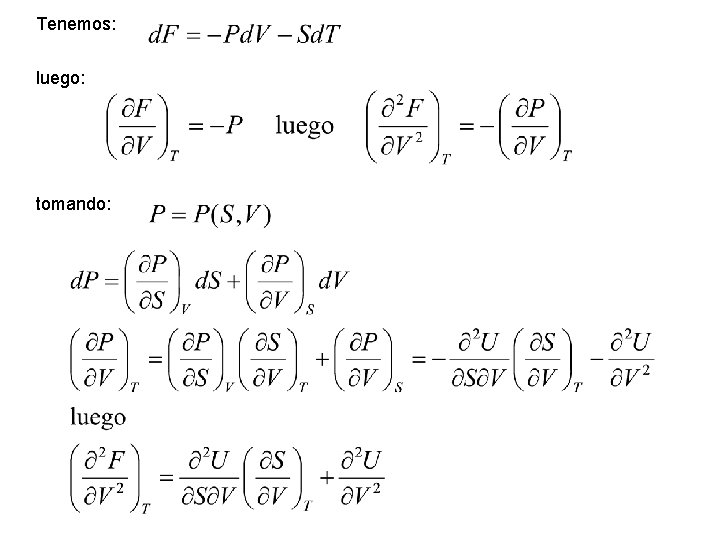




- Slides: 27

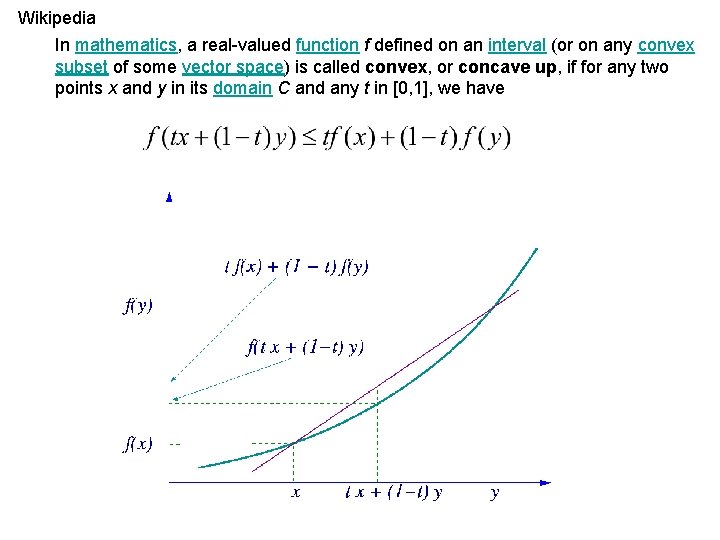
Wikipedia In mathematics, a real-valued function f defined on an interval (or on any convex subset of some vector space) is called convex, or concave up, if for any two points x and y in its domain C and any t in [0, 1], we have

La ecuación de la recta “morada” es: luego: por lo tanto este valor está siempre sobre

Sea: entonces, usando: tenemos Sea ahora: tomando: resulta: Esta es la condición para que la entropía sea una función convexa de la energía interna.

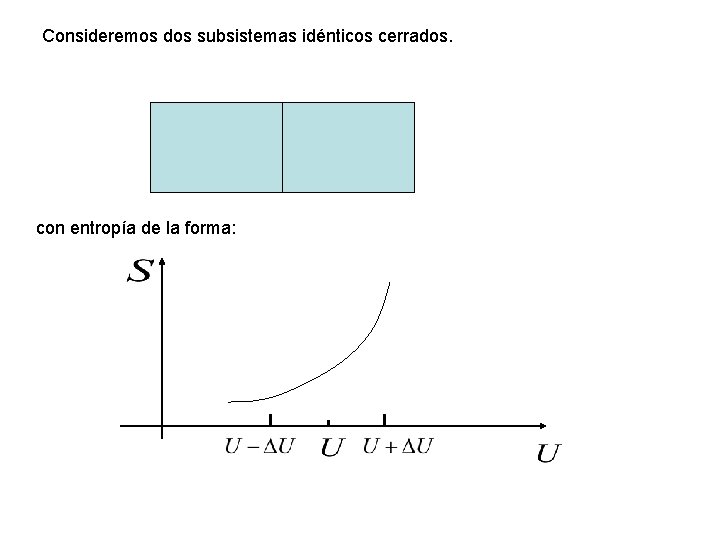
Consideremos dos subsistemas idénticos cerrados. con entropía de la forma:

Se satisface: Por lo tanto si le sacamos, (poniendo una pared diatérmica entre los sistemas), energía de un subsistema tal, para ponérsela al otro, la entropía del sistema compuesto será la cual es mayor que la entropía inicial y el sistema evolucionará espontáneamente hacia este estado de mayor entropía. El sistema era inestable.

La curva será cóncava si la función es convexa, es decir, si se cumple o bien: es decir, análogamente a lo anterior, si se cumple: o bien: En este caso un trasvasije de energía no acarrearía un aumento de la entropía total. El sistema era estable.

Sea y consideremos V y N fijos. sumando: es decir: La entropía es un máximo.

Se hace de manera análoga para V variable y U fijo. Se hace de manera análoga para U y V variables.

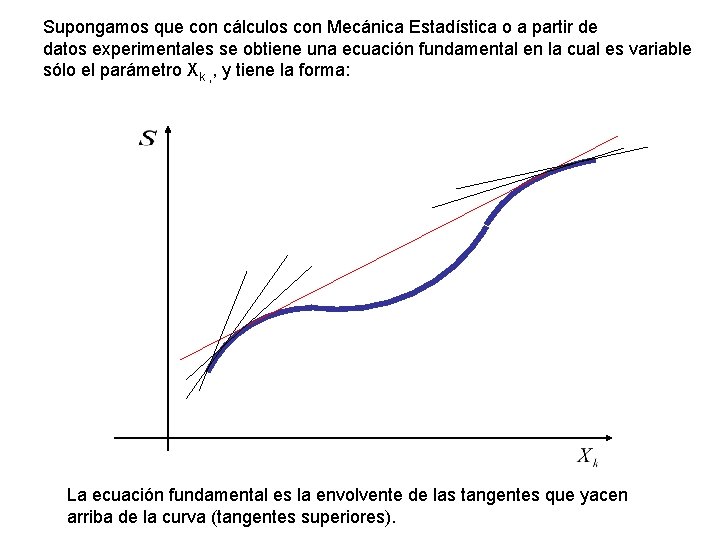
Supongamos que con cálculos con Mecánica Estadística o a partir de datos experimentales se obtiene una ecuación fundamental en la cual es variable sólo el parámetro Xk , , y tiene la forma: La ecuación fundamental es la envolvente de las tangentes que yacen arriba de la curva (tangentes superiores).

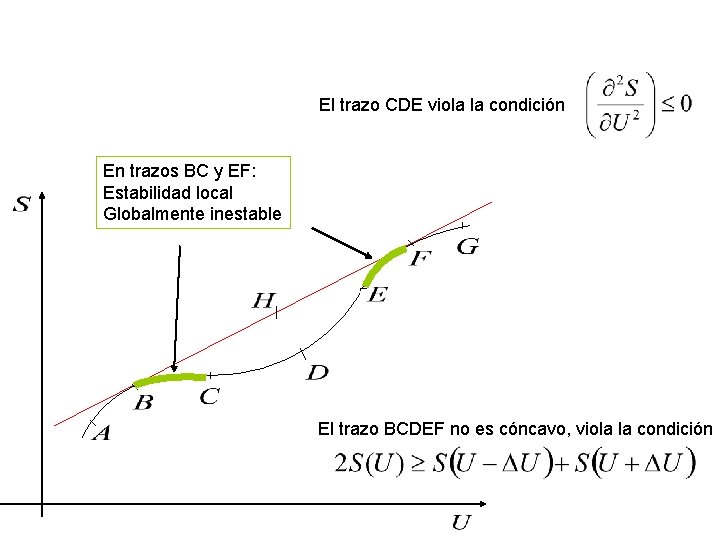
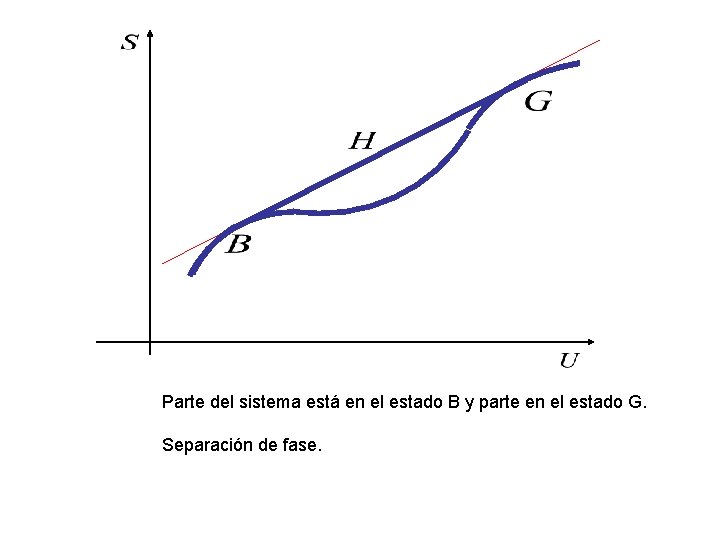
El trazo CDE viola la condición En trazos BC y EF: Estabilidad local Globalmente inestable El trazo BCDEF no es cóncavo, viola la condición

Parte del sistema está en el estado B y parte en el estado G. Separación de fase.

En el caso en que tanto la energía interna como el volumen sean variables, dejando constante N, la superficie de la ecuación fundamental debe estar bajo los planos tangentes, es decir, satisfacer la condición de estabilidad global: Usando la notación: expandimos en Taylor: luego:

son magnitudes arbitrarias e independientes, luego, sin pérdida de generalidad: es decir: son dos condiciones necesarias para la estabilidad.

Considerar la forma: luego: dividiendo por o bien: resulta

Es decir: implica: luego: es otra condición necesaria para la estabilidad.

Resumiendo, las condiciones para la estabilidad son:

Ejemplo: luego: Restricción para la estabilidad

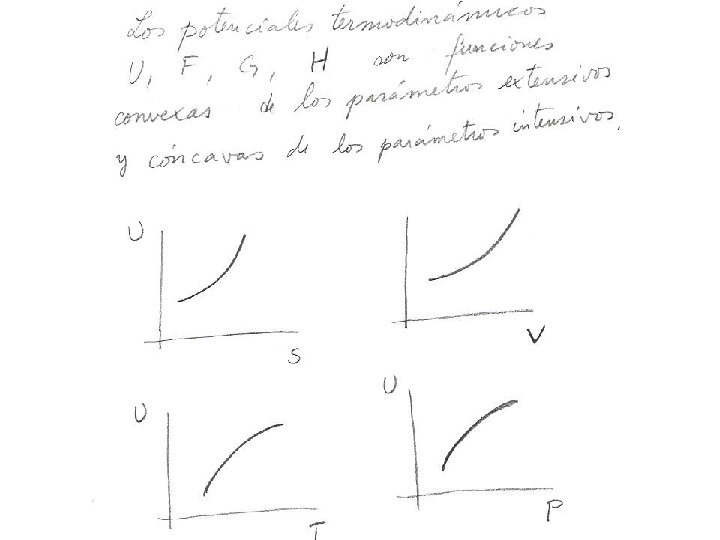
Condiciones de estabilidad para los potenciales termodinámicos. Si la entropía es un máximo la energía es un mínimo; la concavidad de la superficie de la entropía se reemplaza por la convexidad de la superficie de la energía.

Convención para las notaciones: cuando es claro escribimos lo anterior como

Consideremos la energía libre de Helmholtz: luego: pero: luego: La energía libre de Helmholtz es una función cóncava de la temperatura.
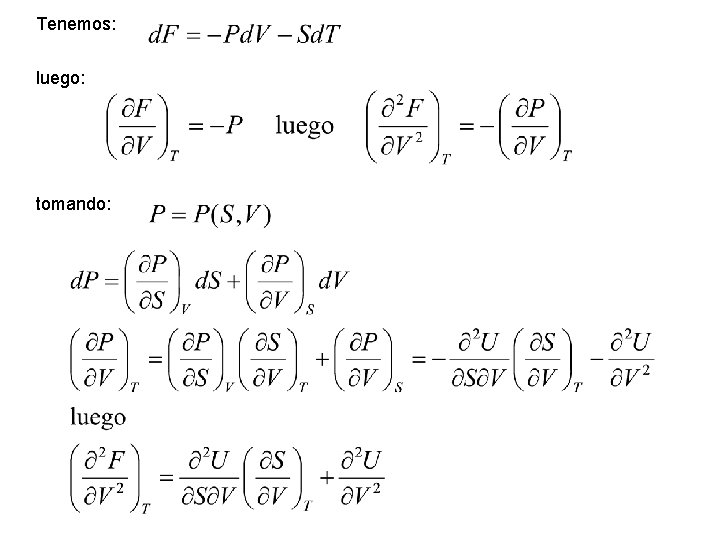
Tenemos: luego: tomando:

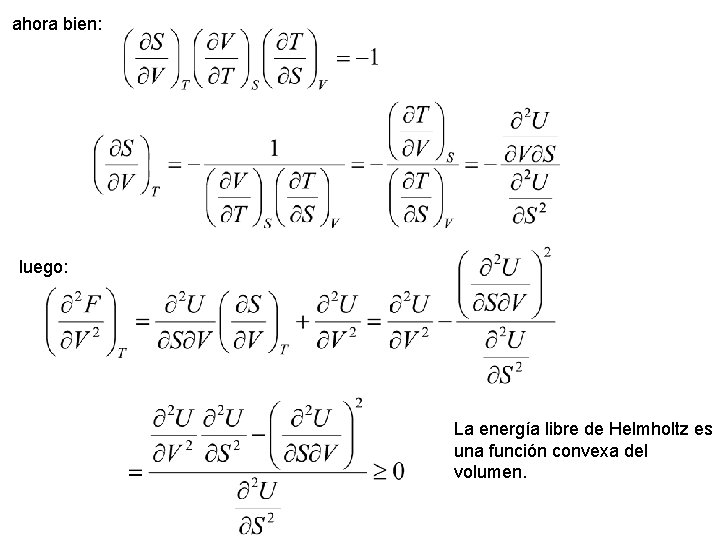
ahora bien: luego: La energía libre de Helmholtz es una función convexa del volumen.

V F T G U S P H d. H=Td. S+Vd. P …. . hacerlo T=T(S, V)



Consecuencias físicas de la estabilidad:
