Why use scientific notation We use very big


Why use scientific notation? • We use very big numbers and very small numbers in chemistry. • It’s hard to do computations with numbers that have lots of zeros in them. • Hard to compare data meaningfully when you are grappling with lots of zeros.
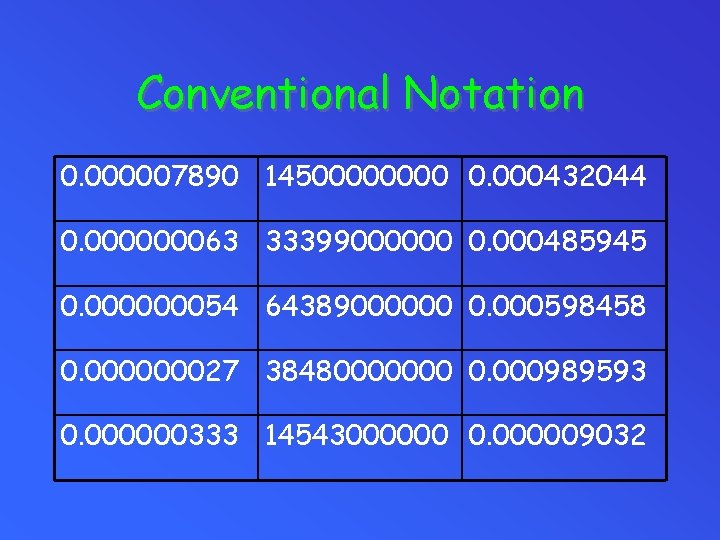
Conventional Notation 0. 000007890 1450000 0. 000432044 0. 000000063 33399000000 0. 000485945 0. 000000054 64389000000 0. 000598458 0. 000000027 38480000000 0. 000989593 0. 000000333 14543000000 0. 000009032

Scientific Notation • The number is written as the product of two other numbers: – A number between 1 and 10 (not 10) and – A power of 10

The exponents • For numbers greater than 1, the exponent will always be positive when you use scientific notation. • For numbers between 0 and 1, the exponent is negative! negative • A negative exponent does not make the number negative.

The only way to make the number negative in scientific notation is to put a negative sign in front of the number!! -4. 8 X 102 is a negative number. 5. 3 X 10 -1 is a positive number.

Converting conventional to scientific notation For numbers 1, 1 the exponent will be positive Count how many places the decimal is moved. 329 3. 29 X 102

Converting conventional to scientific notation For numbers between 0 and 1, 1 the exponent will be negative Count how many places the decimal is moved. 0. 00045 4. 5 X 10 -4

Converting scientific to conventional notation If the exponent is positive, the number 1, so move the decimal point right. 3. 784 X 105 378400

Converting scientific to conventional notation If the exponent is negative, the number is between 0 and 1 so move the decimal point to the left. 2. 75 X 10 -3 0. 00275

Multiplication • Multiply numbers • Add exponents • Convert to proper form if necessary – If you move the decimal left, add to the exponent. – If you move the decimal right, subtract from the exponent.

Practice! (2 X 103)(4 X 102) = 8 X 105 (4 X 102)(6 X 104) = 24 X 106 = 2. 4 X 107 (3 X 104)(5 X 10 -2) = 15 X 102 = 1. 5 X 103

Division • Divide numbers • Subtract exponents • Convert to proper form if necessary – If you move the decimal left, add to the exponent. – If you move the decimal right, subtract from the exponent.
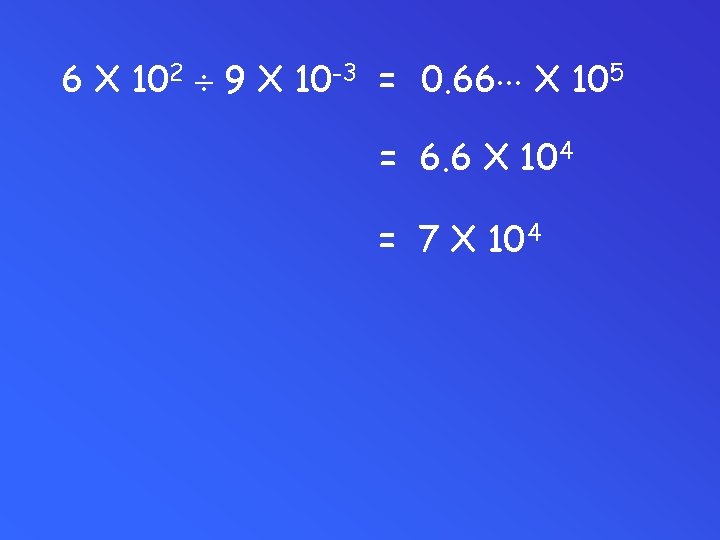
6 X 102 9 X 10 -3 = 0. 66 X 105 = 6. 6 X 104 = 7 X 104

Addition and Subtraction • Convert to common exponent if necessary – If you have to increase the exponent, move the decimal to the left. – If you have to decrease the exponent, move the decimal to the right. • Add or subtract numbers • Maintain exponent • Convert to proper form if necessary
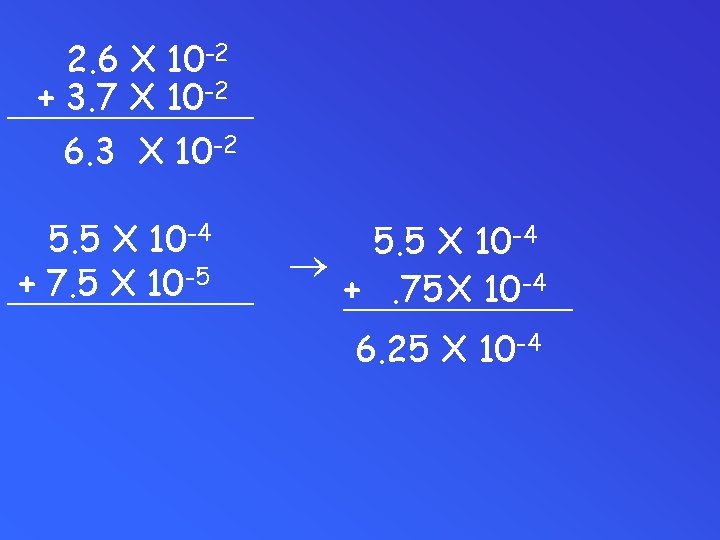
2. 6 X 10 -2 -2 + 3. 7 X 10 _______ 6. 3 X 10 -2 5. 5 X 10 -4 -5 + 7. 5 X 10 _______ 5. 5 X 10 -4 +_______. 75 X 10 -4 6. 25 X 10 -4
- Slides: 16