Why use phylogenetic networks to visualize data when

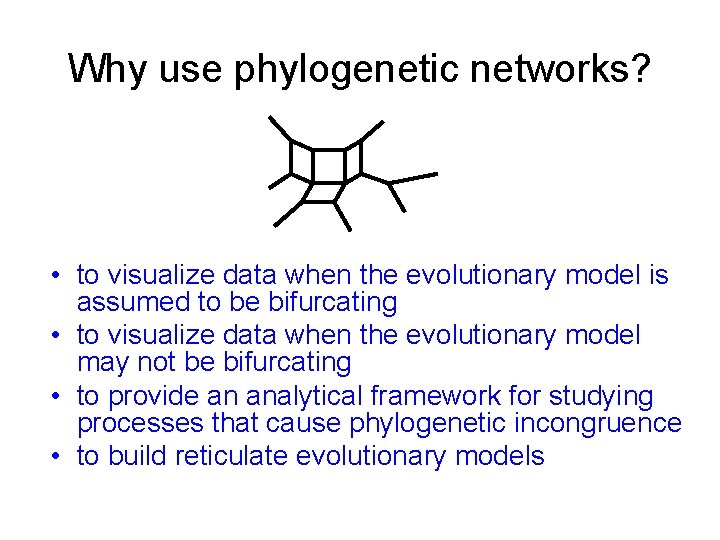
Why use phylogenetic networks? • to visualize data when the evolutionary model is assumed to be bifurcating • to visualize data when the evolutionary model may not be bifurcating • to provide an analytical framework for studying processes that cause phylogenetic incongruence • to build reticulate evolutionary models

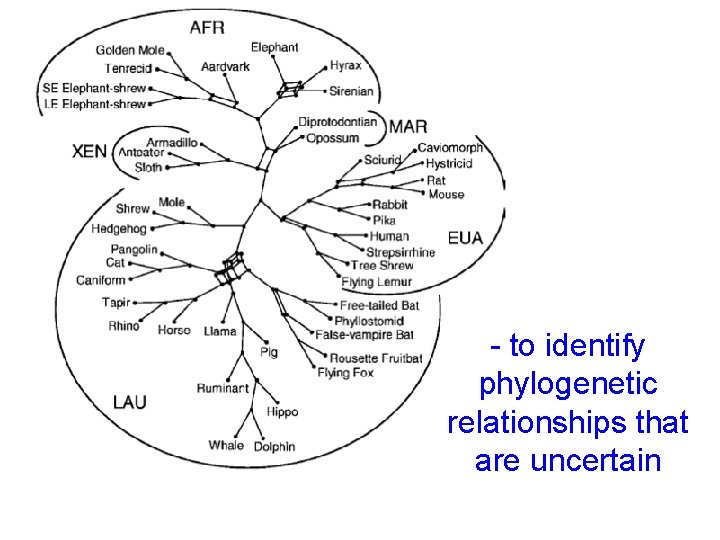
- to identify phylogenetic relationships that are uncertain

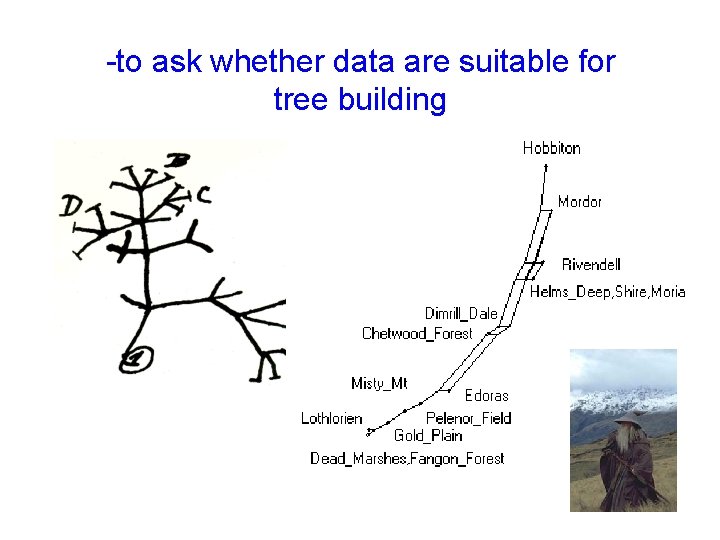
-to ask whether data are suitable for tree building

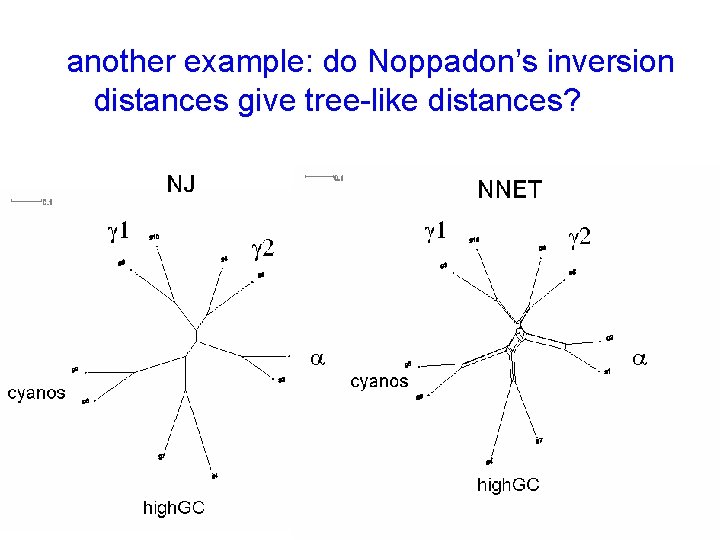
another example: do Noppadon’s inversion distances give tree-like distances?

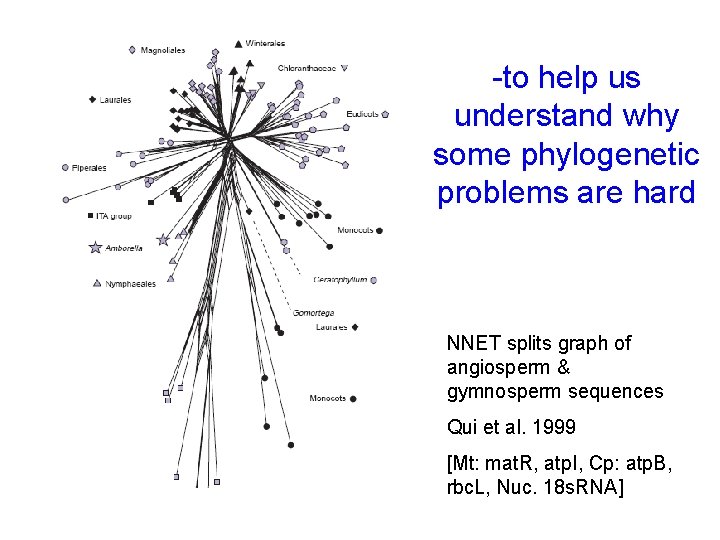
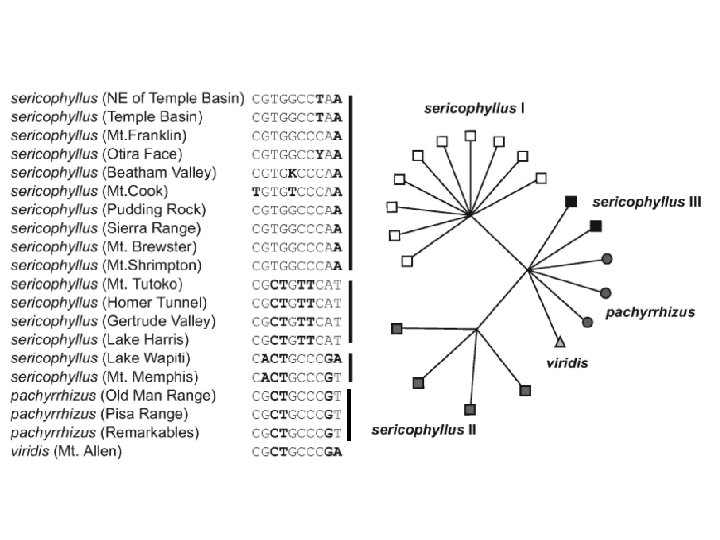
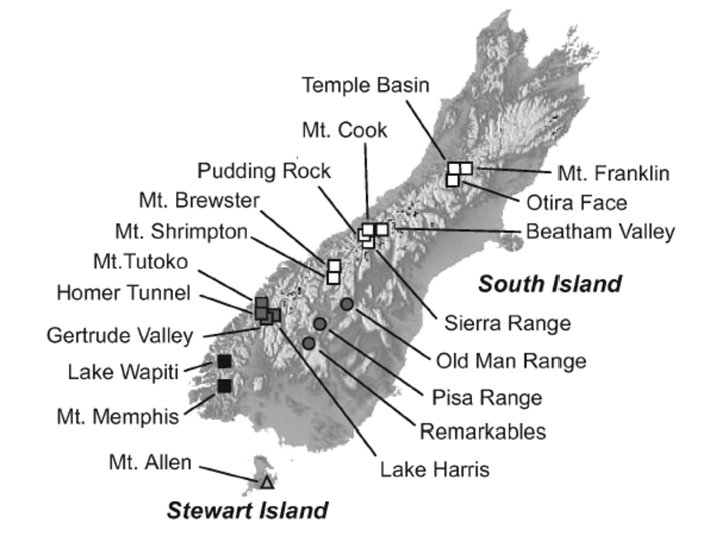
-to help us understand why some phylogenetic problems are hard NNET splits graph of angiosperm & gymnosperm sequences Qui et al. 1999 [Mt: mat. R, atp. I, Cp: atp. B, rbc. L, Nuc. 18 s. RNA]

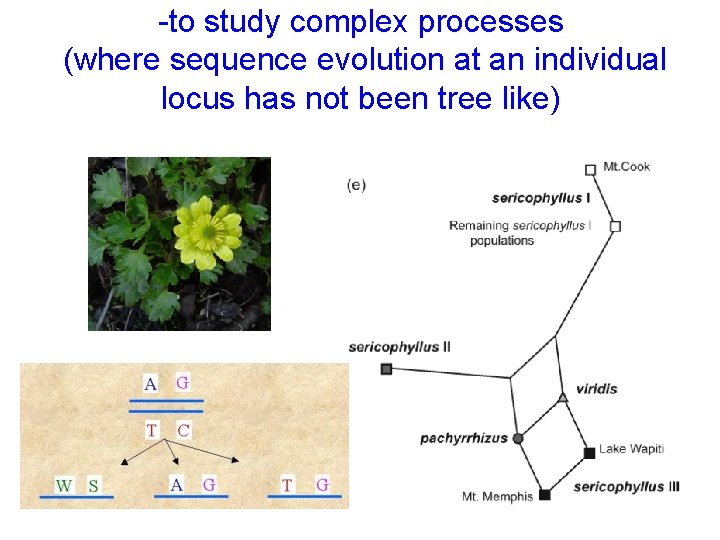
-to study complex processes (where sequence evolution at an individual locus has not been tree like)

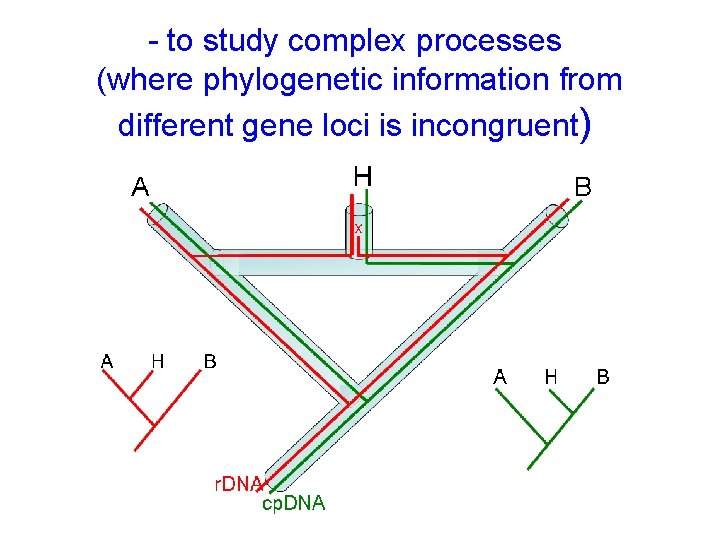
- to study complex processes (where phylogenetic information from different gene loci is incongruent)

- to study complex processes (where phylogenetic information from different gene loci is incongruent)

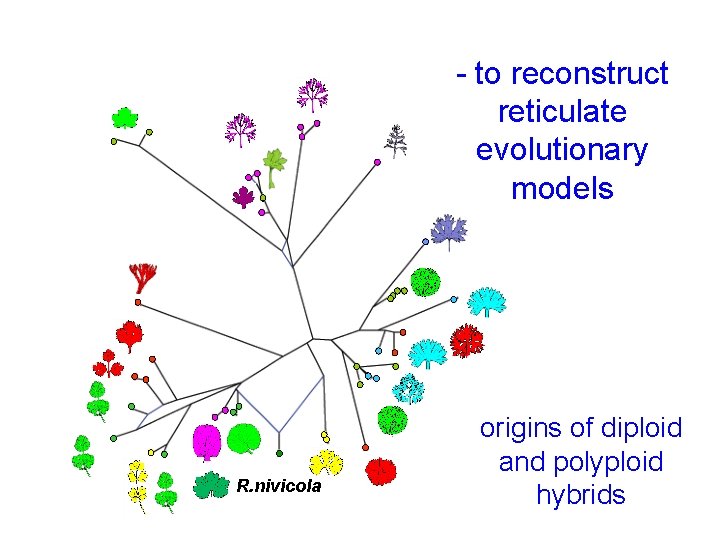
- to reconstruct reticulate evolutionary models R. nivicola origins of diploid and polyploid hybrids

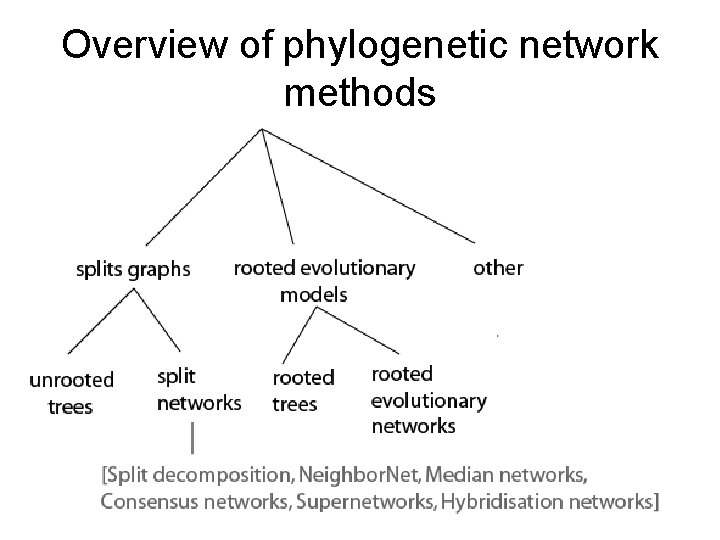
Overview of phylogenetic network methods

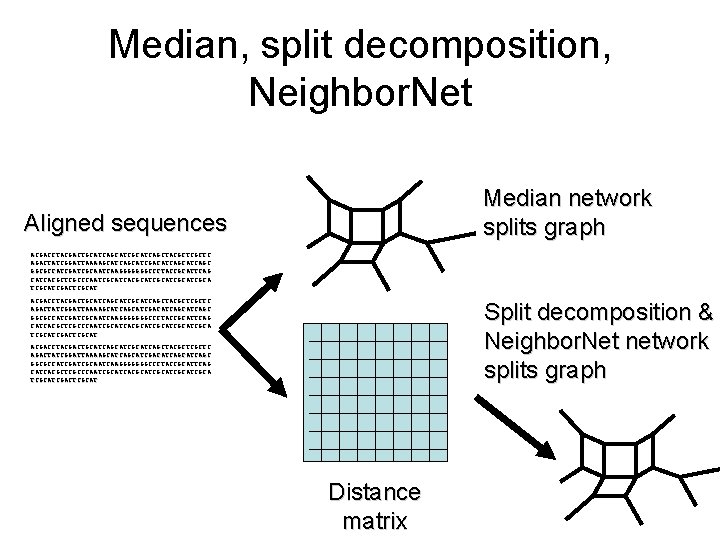
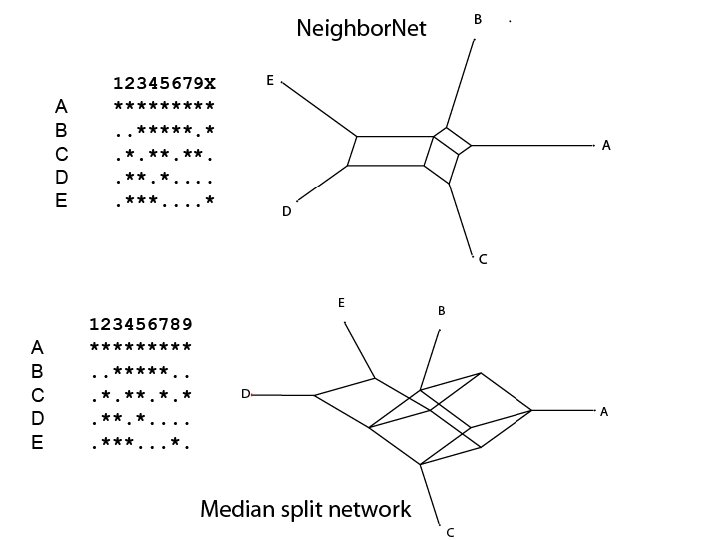
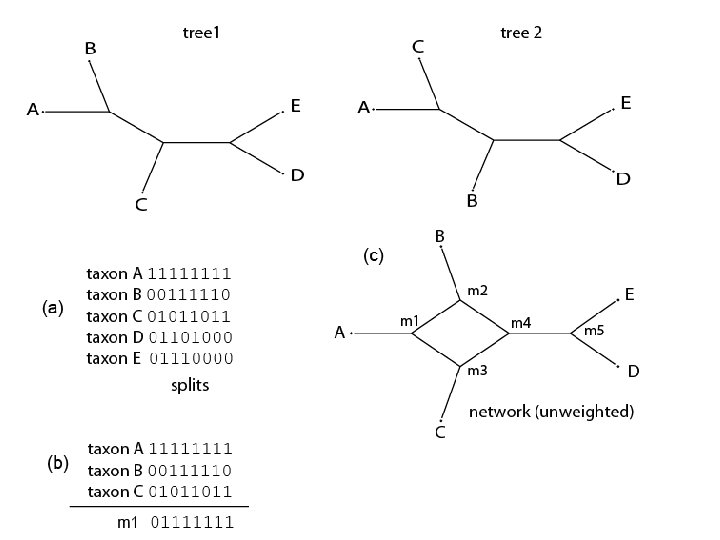
Median, split decomposition, Neighbor. Net Median network splits graph Aligned sequences ACGACCTACGACTGCATCAGCATCGCATCAGCTACGCTCGCTC AGACTATCGGATTAAAAGCATCAGCATCGACATCAGCATCAGC GGCGCCATCGATCGCAATCAAGGGGGGGCCCTACCGCATTCAG CATCACGCTCGCCCAATCGCATCACGCATCGCATCGCATCGCATCGACTCGCAT Split decomposition & Neighbor. Net network splits graph ACGACCTACGACTGCATCAGCATCAGCTACGCTC AGACTATCGGATTAAAAGCATCGACATCAGC GGCGCCATCGCAATCAAGGGGGGGCCCTACCGCATTCAG CATCACGCTCGCCCAATCGCATCACGCATCGCATCGCATCGACTCGCAT Distance matrix

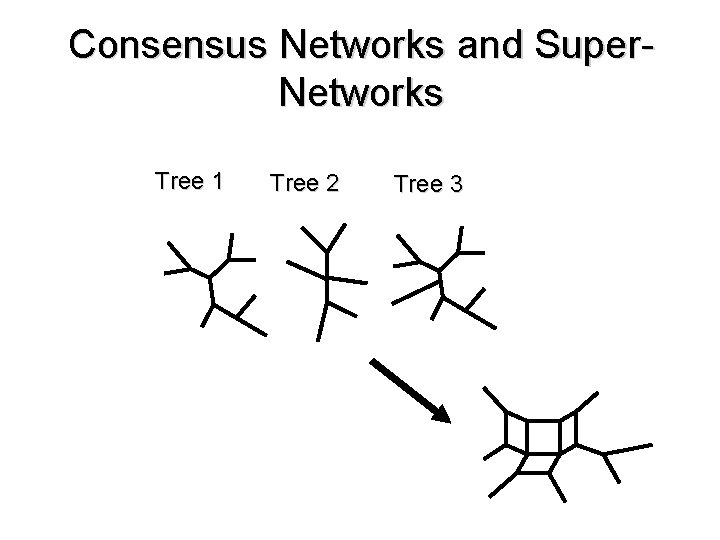
Consensus Networks and Super. Networks Tree 1 Tree 2 Tree 3

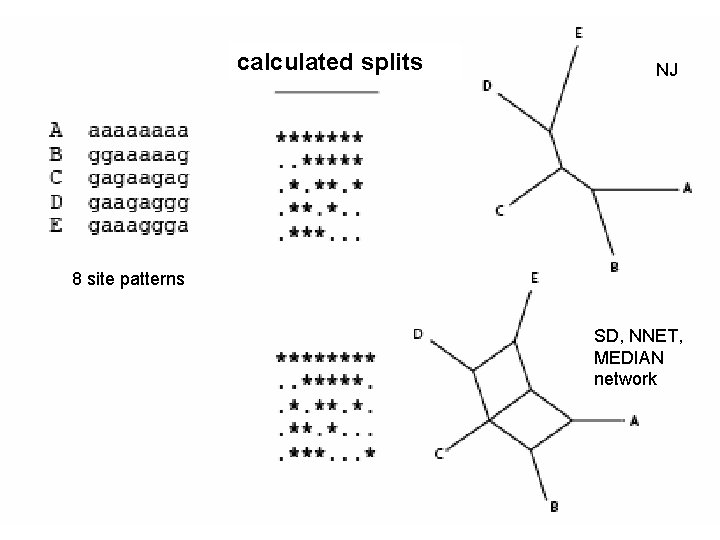
site patterns, splits graph site patterns observed splits graph

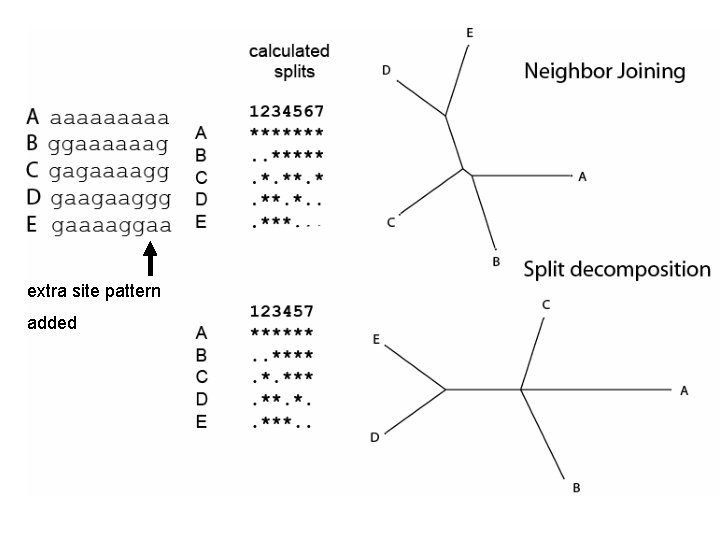
calculated splits NJ 8 site patterns SD, NNET, MEDIAN network

extra site pattern added

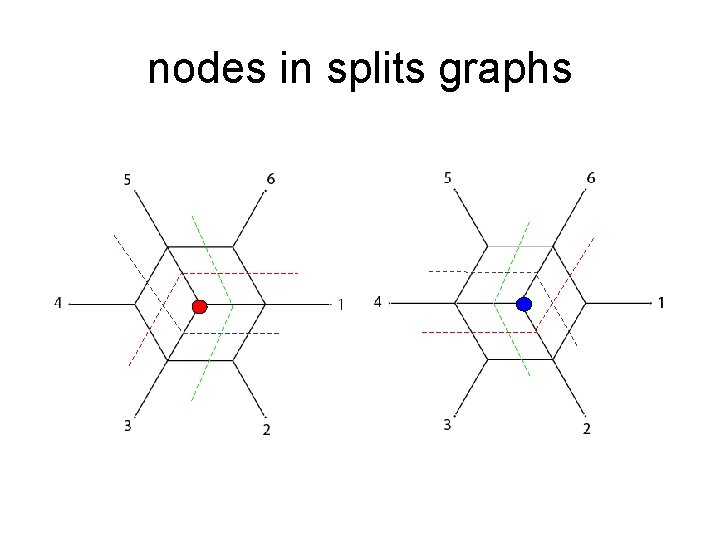
nodes in splits graphs

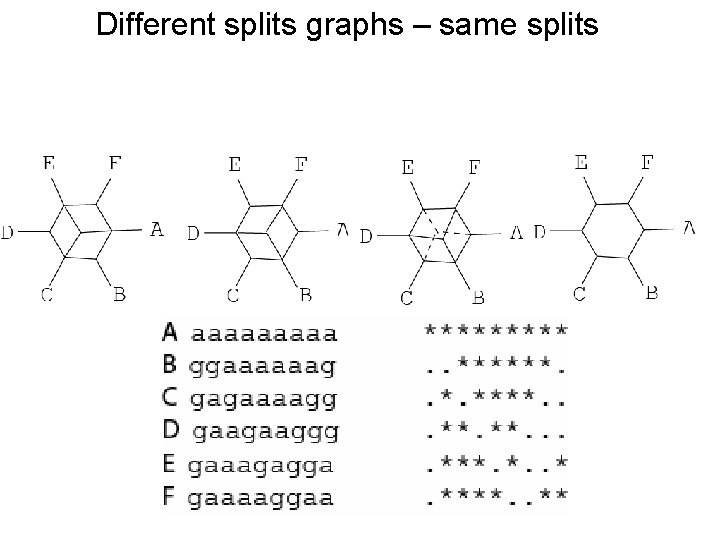
Different splits graphs – same splits

summary • Different reasons why you might want to build a phylogenetic network • Some network methods identify more splits in the data than other methods • there may be more than one splits graph representation for a set of splits • Nodes in splits graph are not equivalent to the nodes in trees

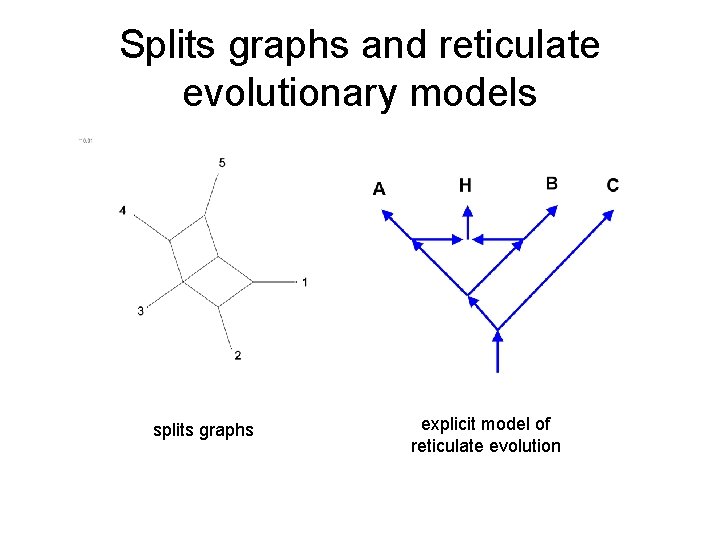
Splits graphs and reticulate evolutionary models splits graphs explicit model of reticulate evolution

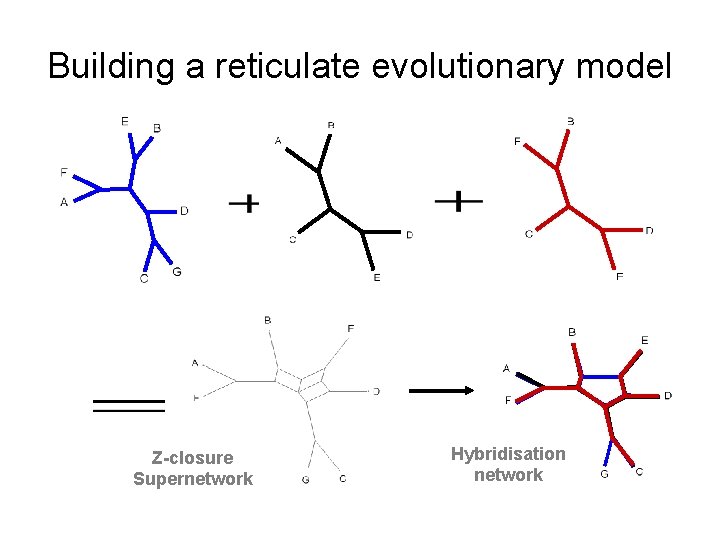
Building a reticulate evolutionary model Z-closure Supernetwork Hybridisation network

Daniel Huson and David Bryant

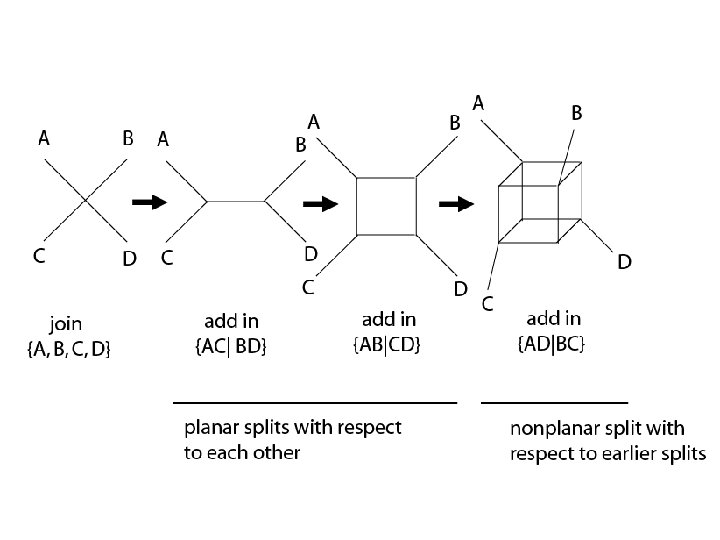
Split decomposition • Identify weakly compatible splits for all possible combinations of quartets • Define split lengths for all splits in split system • Build splits graph

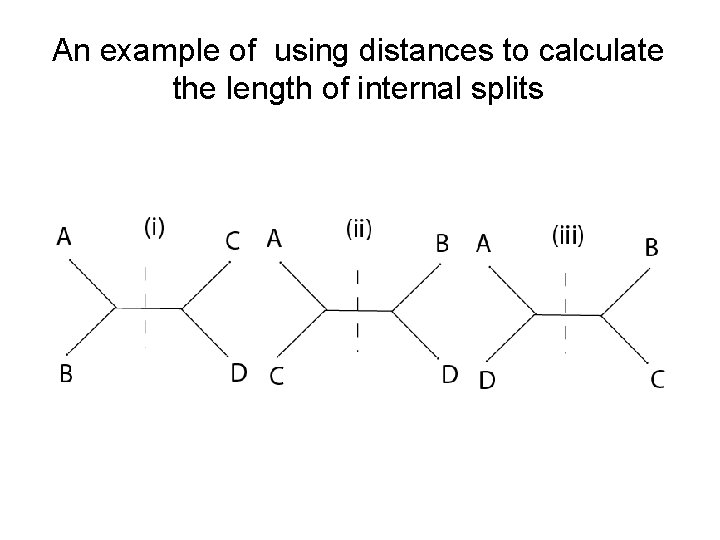
An example of using distances to calculate the length of internal splits

distance matrix calculated from sequences • • A B C D 3 6 5 5 6 9 AB|CD AC|BD AD|BC

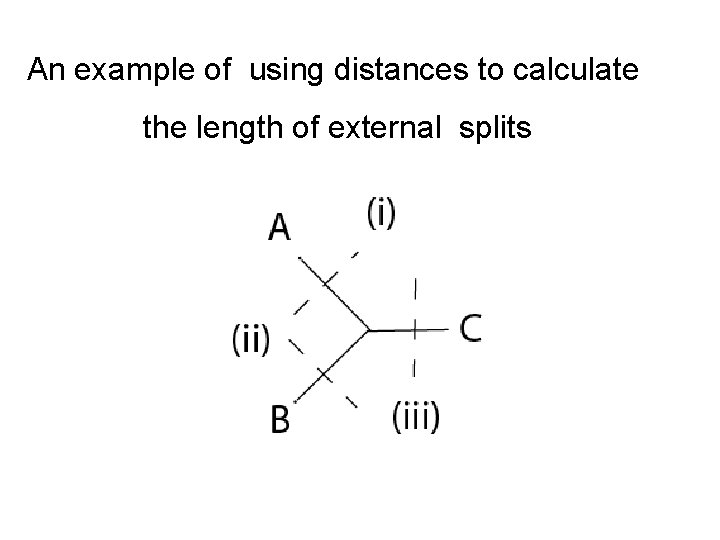
An example of using distances to calculate the length of external splits

example • • A B C D 3 6 5 5 6 9 A|CD A|BC

Neighbor. Net (NNET) • Use Neighbor. Joining like algorithms to determine the order in which sequences (nodes) can be joined to give a circular ordering. • Once you have the circular ordering, use least squares to identify all splits with positive (non zero) lengths • Build splits graph

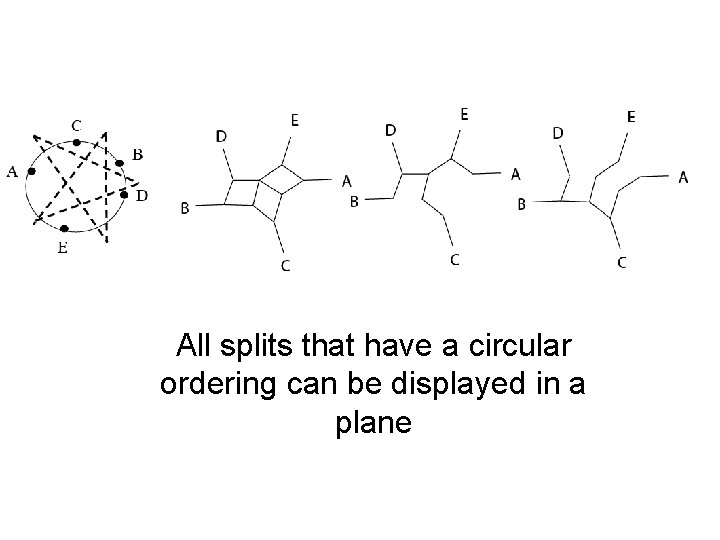
All splits that have a circular ordering can be displayed in a plane

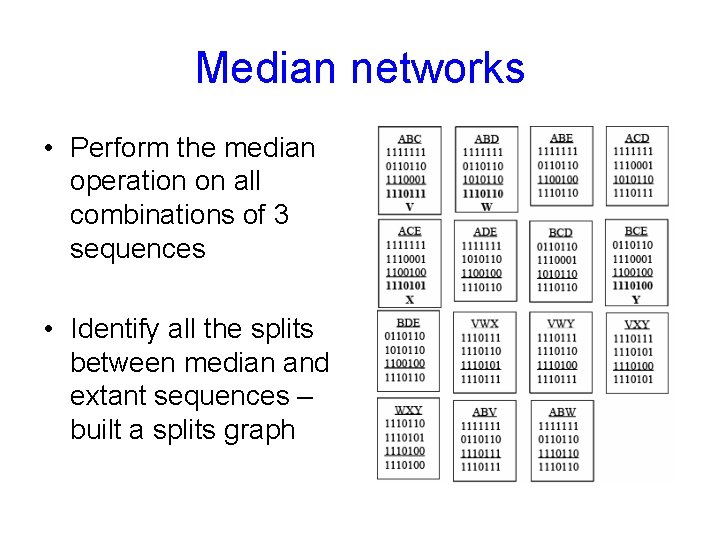
Median networks • Perform the median operation on all combinations of 3 sequences • Identify all the splits between median and extant sequences – built a splits graph

Consensus networks • Extends idea of median networks to splits calculated from trees

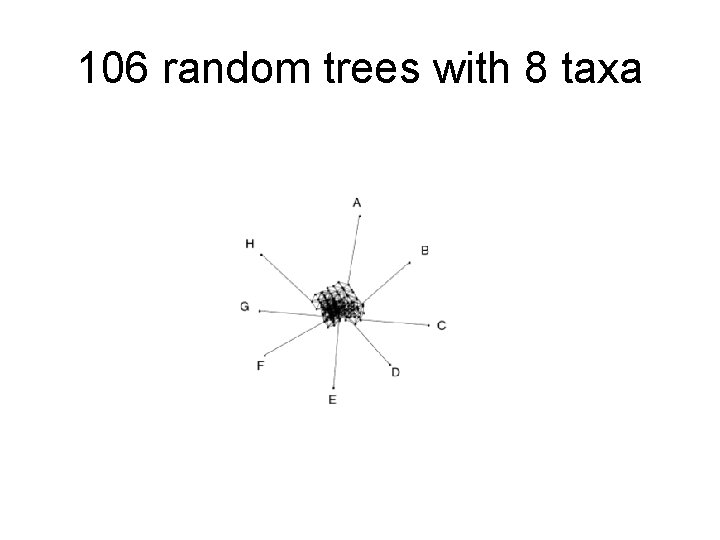
106 random trees with 8 taxa

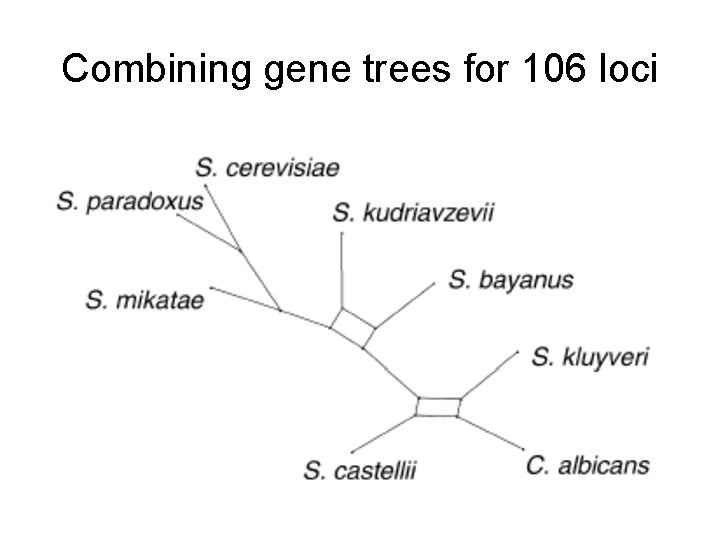
Combining gene trees for 106 loci

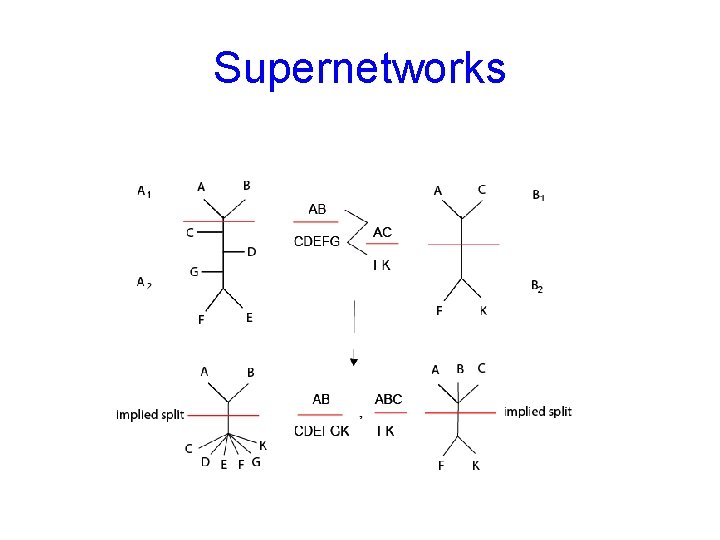
Supernetworks

More detail about building a splits graph…. .

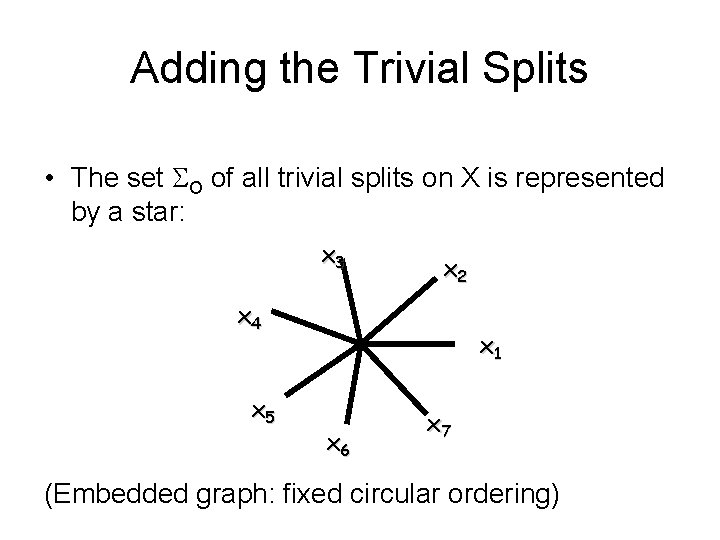
Adding the Trivial Splits • The set O of all trivial splits on X is represented by a star: x 3 x 2 x 4 x 5 x 1 x 6 x 7 (Embedded graph: fixed circular ordering)

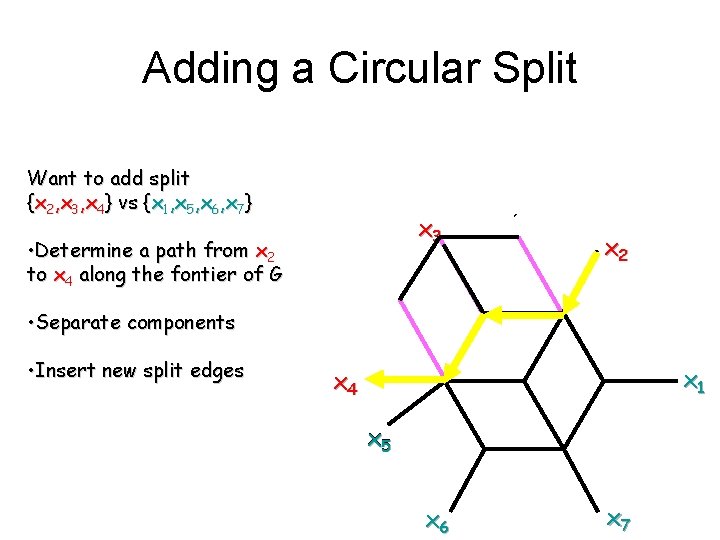
Adding a Circular Split Want to add split {x 2, x 3, x 4} vs {x 1, x 5, x 6, x 7} x 3 • Determine a path from x 2 to x 4 along the fontier of G x 2 • Separate components • Insert new split edges x 1 x 4 x 5 x 6 x 7

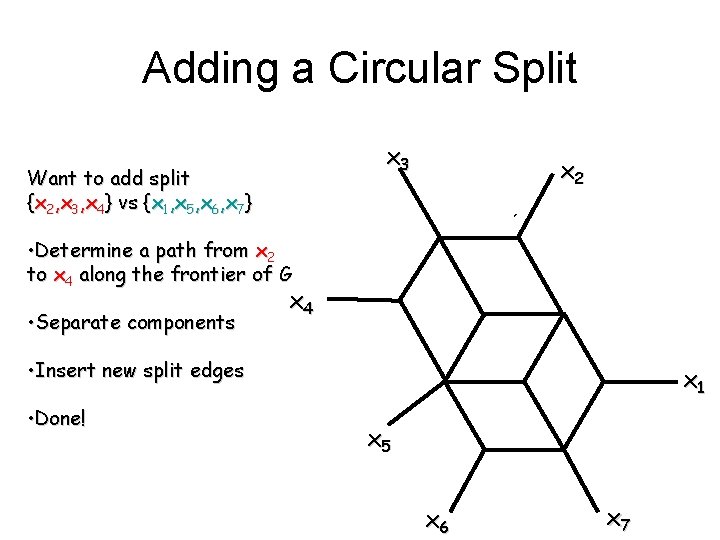
Adding a Circular Split x 3 Want to add split {x 2, x 3, x 4} vs {x 1, x 5, x 6, x 7} x 2 • Determine a path from x 2 to x 4 along the frontier of G • Separate components x 4 • Insert new split edges • Done! x 1 x 5 x 6 x 7

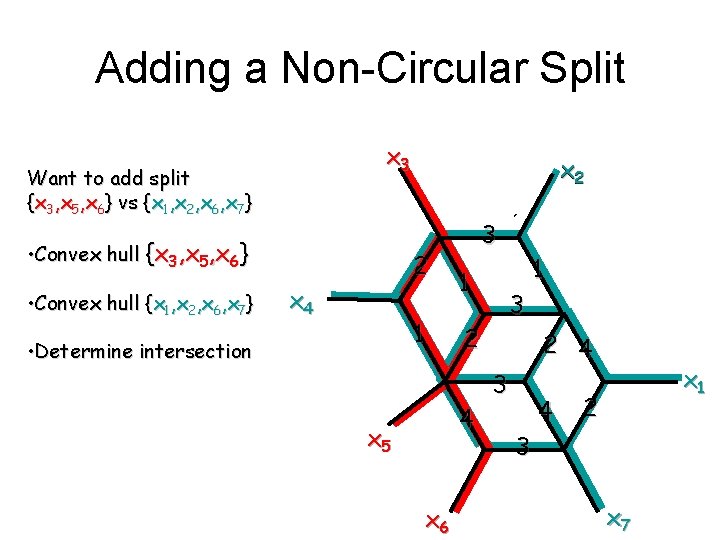
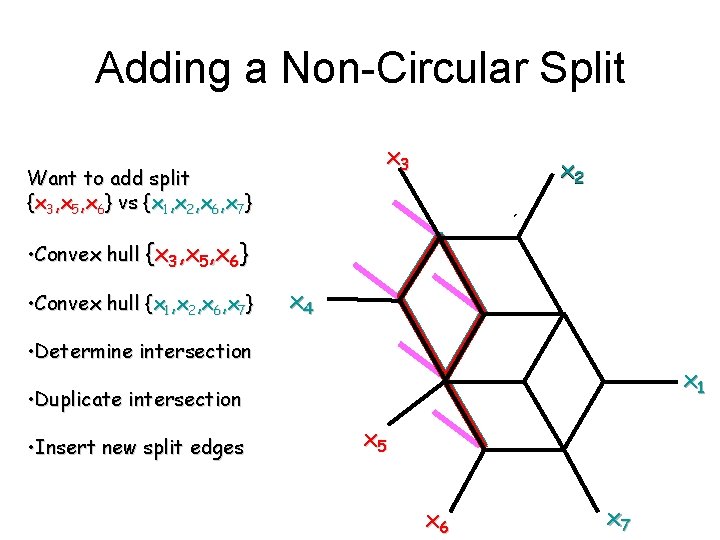
Adding a Non-Circular Split x 3 Want to add split {x 3, x 5, x 6} vs {x 1, x 2, x 6, x 7} • Convex hull {x 3, x 5, x 6} • Convex hull {x 1, x 2, x 6, x 7} x 2 2 x 4 1 • Determine intersection 3 1 3 2 4 x 5 x 6 1 2 4 3 4 x 1 2 3 x 7

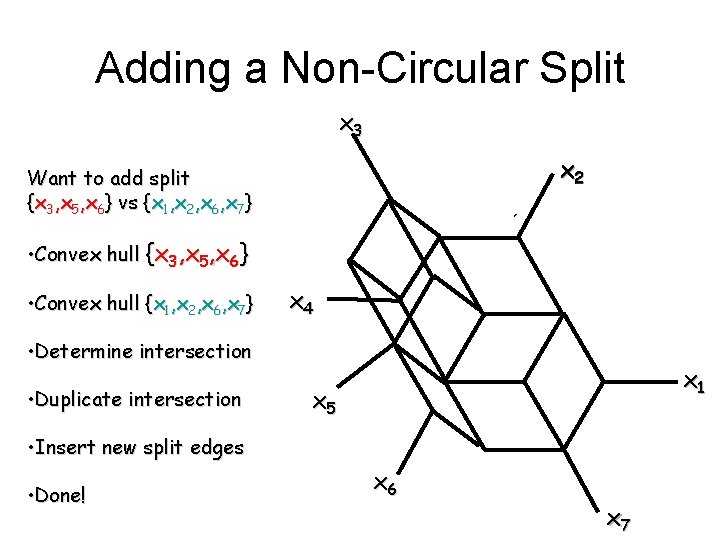
Adding a Non-Circular Split x 3 Want to add split {x 3, x 5, x 6} vs {x 1, x 2, x 6, x 7} x 2 • Convex hull {x 3, x 5, x 6} • Convex hull {x 1, x 2, x 6, x 7} x 4 • Determine intersection x 1 • Duplicate intersection • Insert new split edges x 5 x 6 x 7

Adding a Non-Circular Split x 3 x 2 Want to add split {x 3, x 5, x 6} vs {x 1, x 2, x 6, x 7} • Convex hull {x 3, x 5, x 6} • Convex hull {x 1, x 2, x 6, x 7} x 4 • Determine intersection • Duplicate intersection x 1 x 5 • Insert new split edges • Done! x 6 x 7