Why is the QuarkGluon Plasma Perfect Liquid a

Why is the Quark-Gluon Plasma “Perfect” Liquid ? a Berndt Mueller – YITP / Duke RIKEN Workshop Special thanks to M. Asakawa and S. A. Bass 8 -9 July 2006 1

Lecture I n What does Lattice QCD tell us about the QGP ? n What do RHIC experiments tell us about the QGP ? n What is a “perfect” fluid ? n What are the origins of viscosity ? 2

What does Lattice QCD tell us about the QGP ? A: So far, a lot about thermodynamic properties and response to static probes, a little bit about spectral functions, (almost) nothing about transport properties. 3

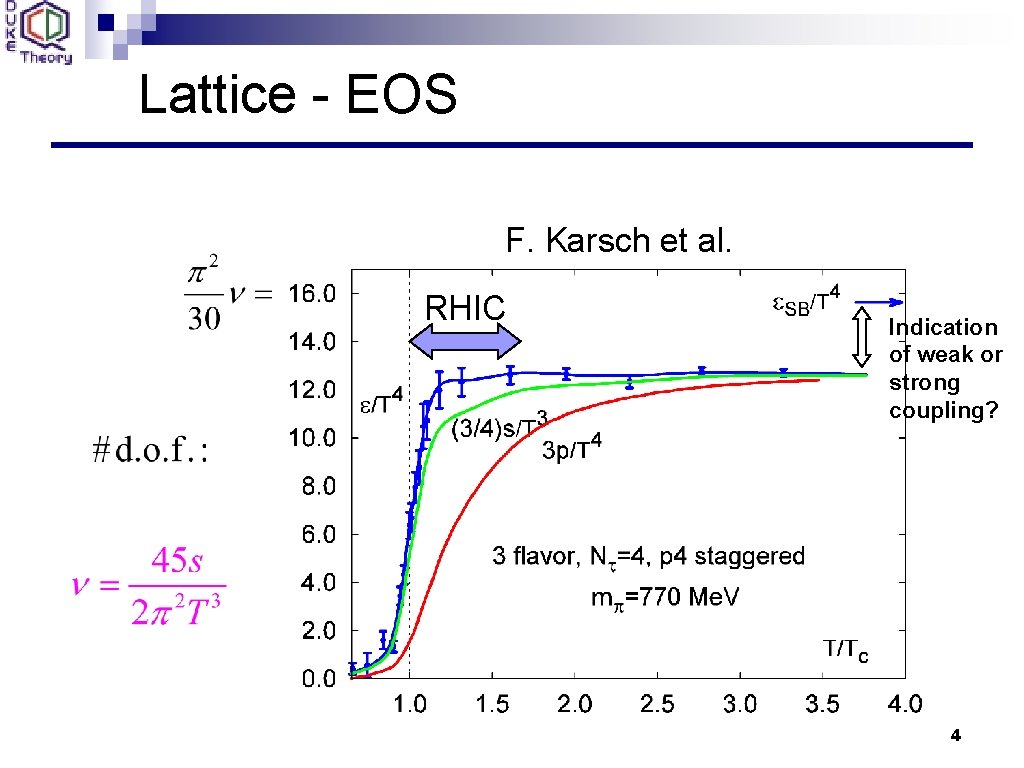
Lattice - EOS F. Karsch et al. RHIC Indication of weak or strong coupling? 4

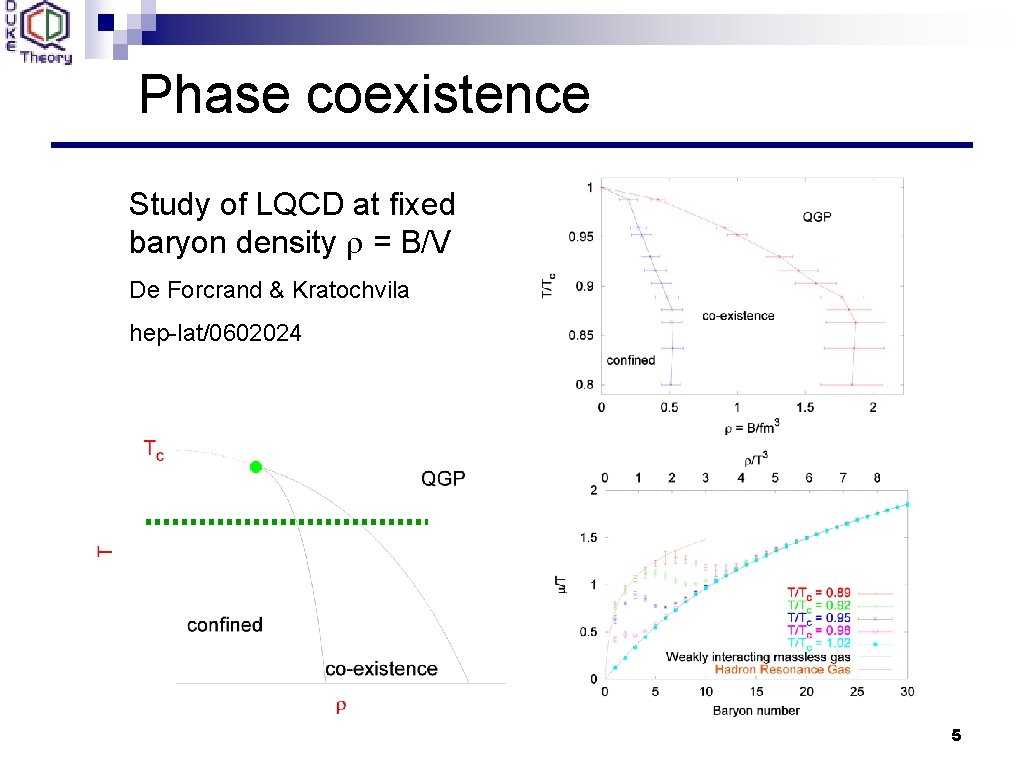
Phase coexistence Study of LQCD at fixed baryon density r = B/V De Forcrand & Kratochvila hep-lat/0602024 5

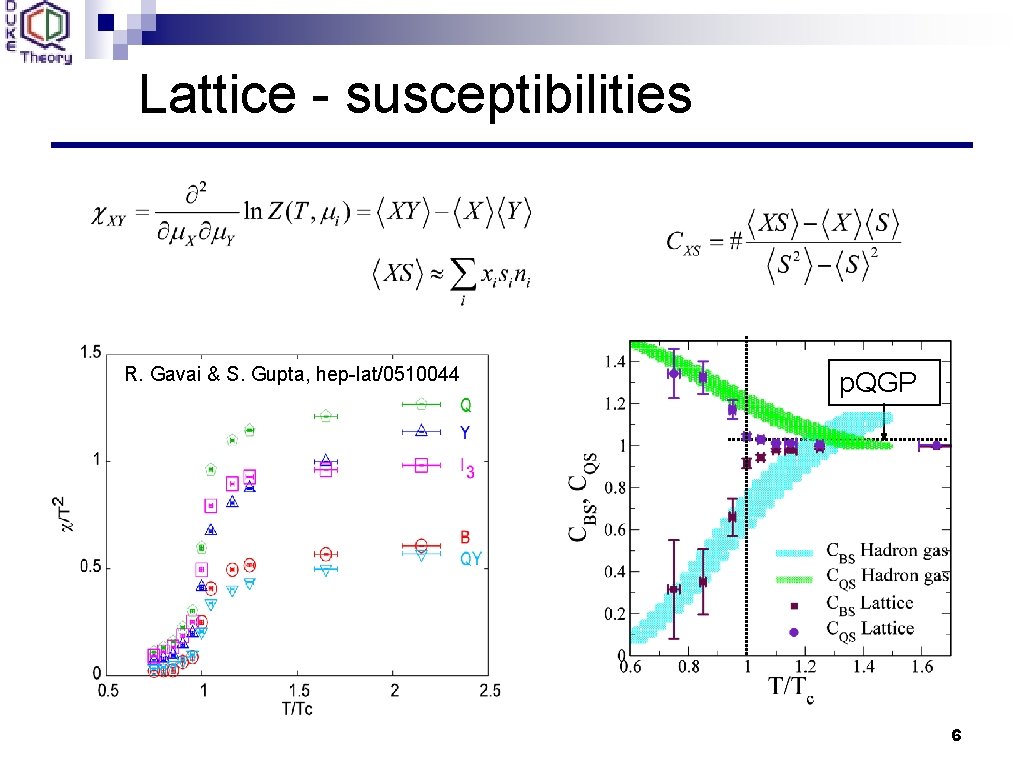
Lattice - susceptibilities R. Gavai & S. Gupta, hep-lat/0510044 p. QGP 6

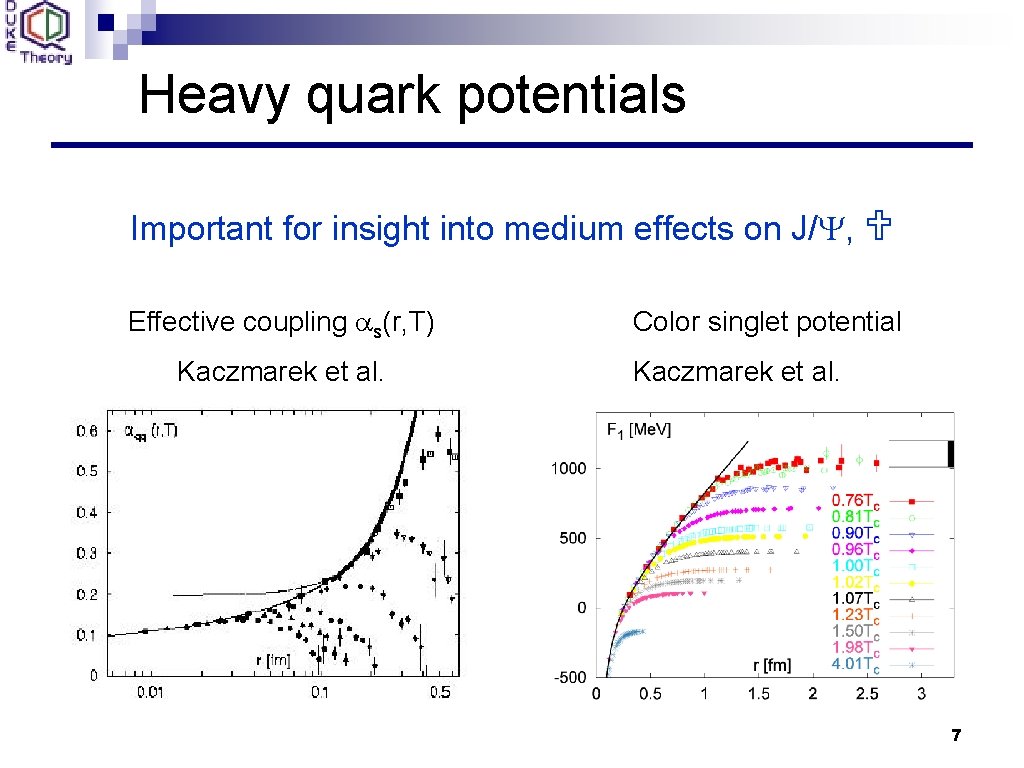
Heavy quark potentials Important for insight into medium effects on J/Y, Effective coupling as(r, T) Kaczmarek et al. Color singlet potential Kaczmarek et al. 7

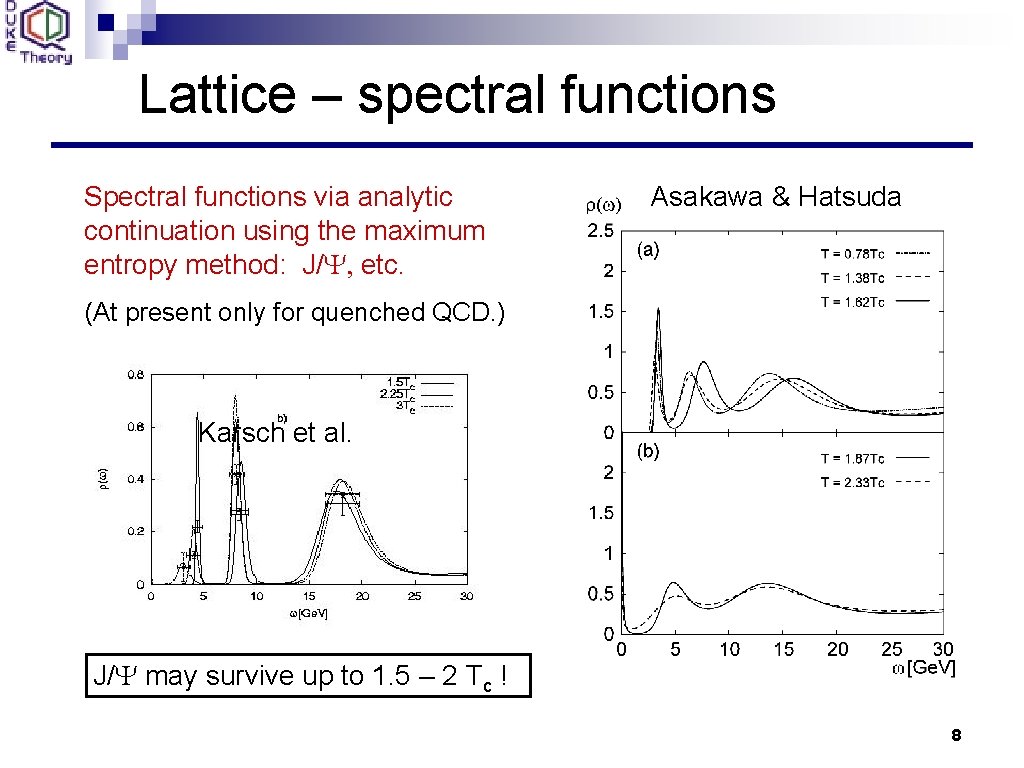
Lattice – spectral functions Spectral functions via analytic continuation using the maximum entropy method: J/Y, etc. Asakawa & Hatsuda (At present only for quenched QCD. ) Karsch et al. J/Y may survive up to 1. 5 – 2 Tc ! 8

What do RHIC experiments tell us about the QGP ? A: So far, a lot about transport properties, a little bit about thermodynamic properties, and (almost) nothing about spectral functions and response to static probes. 9

The real road to the QGP …is the Relativistic Heavy Ion Collider STAR 10

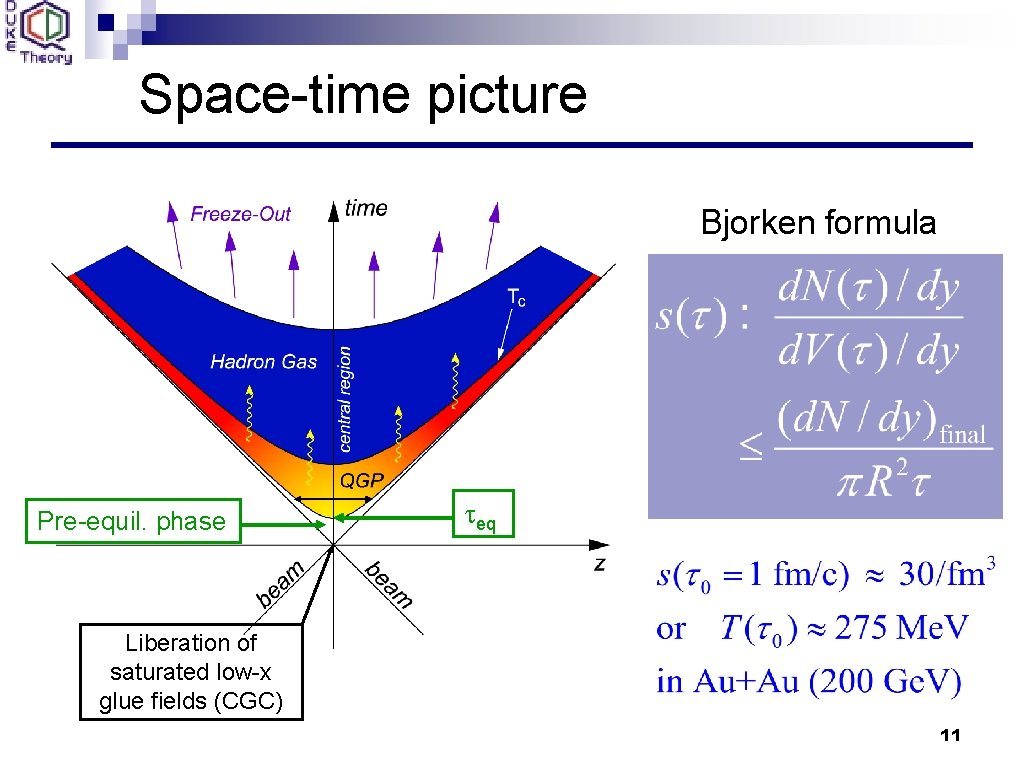
Space-time picture Bjorken formula Pre-equil. phase teq Liberation of saturated low-x glue fields (CGC) 11

RHIC results Important results from RHIC: n n n n Chemical (flavor) and thermal equilibration Jet quenching = parton energy loss, high opacity Elliptic flow = early thermalization, low viscosity Collective flow pattern related to valence quarks Strong energy loss of c and b quarks Charmonium suppression not significantly increased compared with lower (CERN) energies Photons unaffected by medium at high p. T, medium emission at low p. T in agreement with models 12

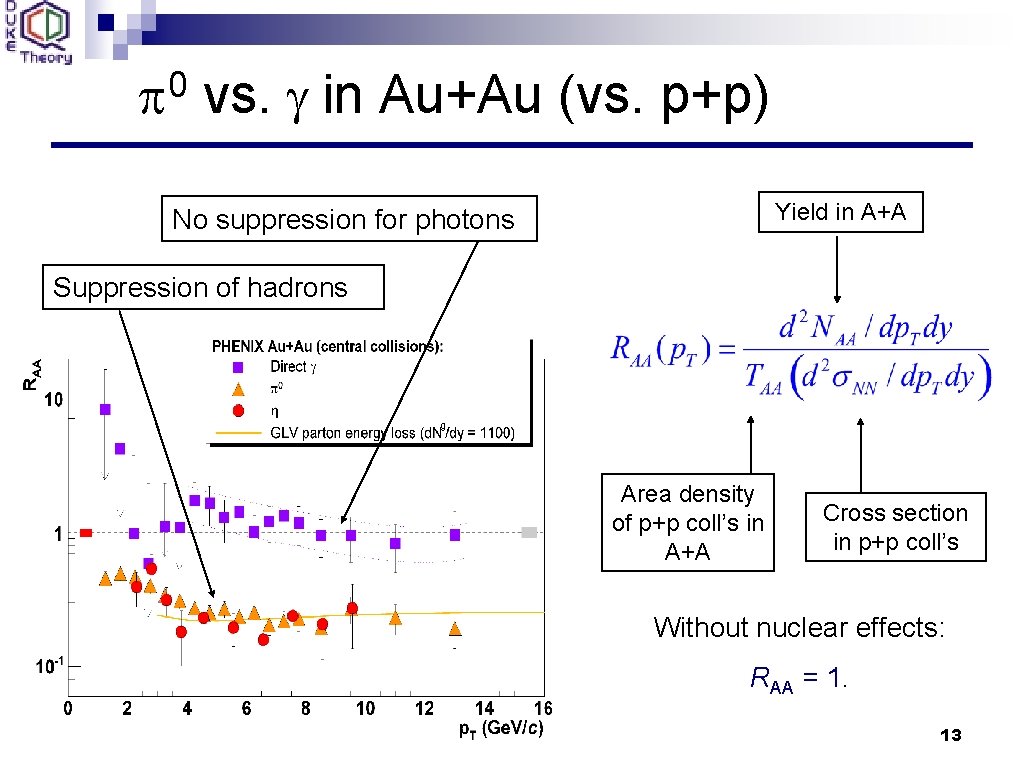
0 p vs. g in Au+Au (vs. p+p) Yield in A+A No suppression for photons Suppression of hadrons Area density of p+p coll’s in A+A Cross section in p+p coll’s Without nuclear effects: RAA = 1. 13

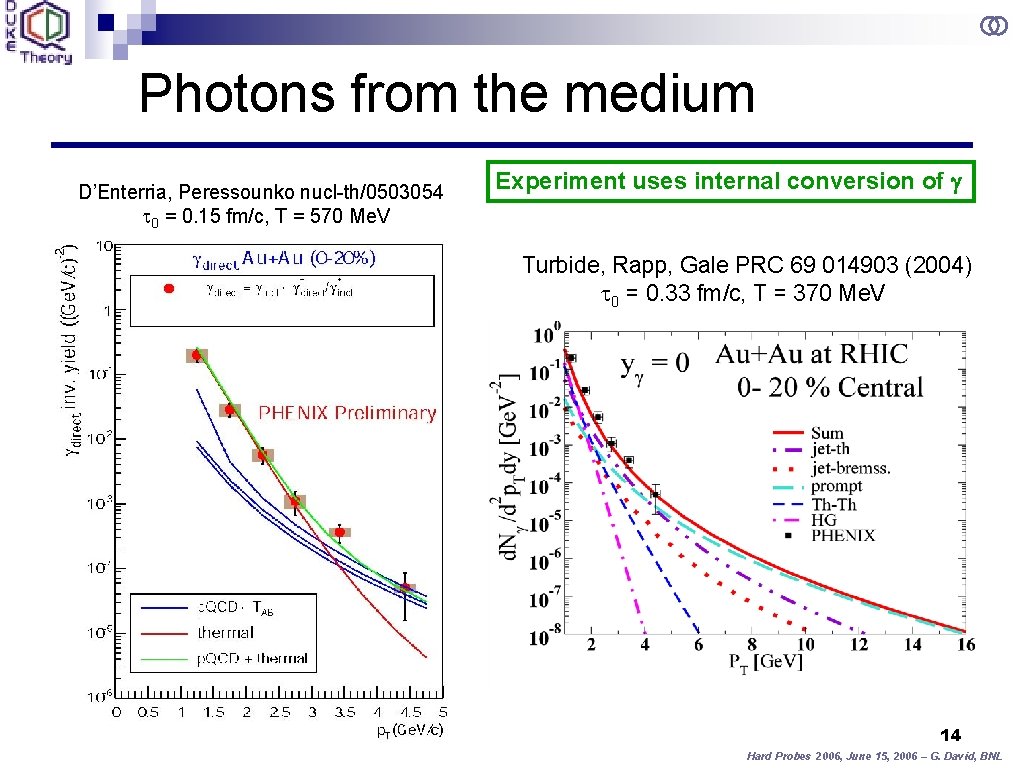
Photons from the medium D’Enterria, Peressounko nucl-th/0503054 t 0 = 0. 15 fm/c, T = 570 Me. V Experiment uses internal conversion of g Turbide, Rapp, Gale PRC 69 014903 (2004) t 0 = 0. 33 fm/c, T = 370 Me. V 14 Hard Probes 2006, June 15, 2006 – G. David, BNL

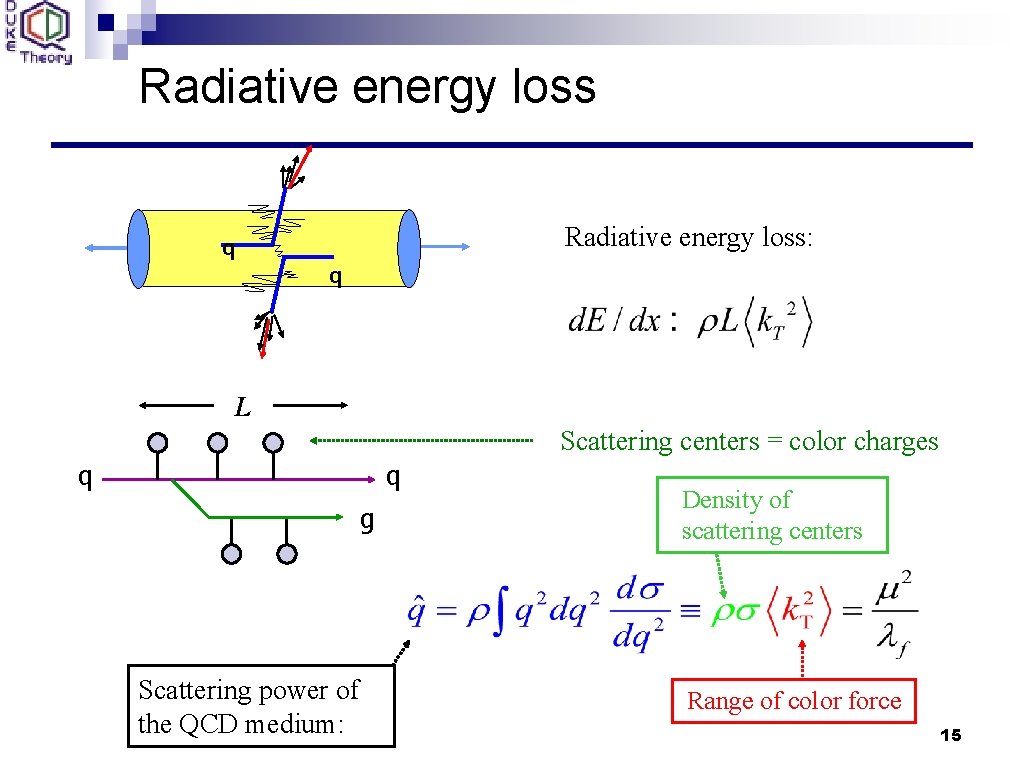
Radiative energy loss: q q L Scattering centers = color charges q q g Scattering power of the QCD medium: Density of scattering centers Range of color force 15

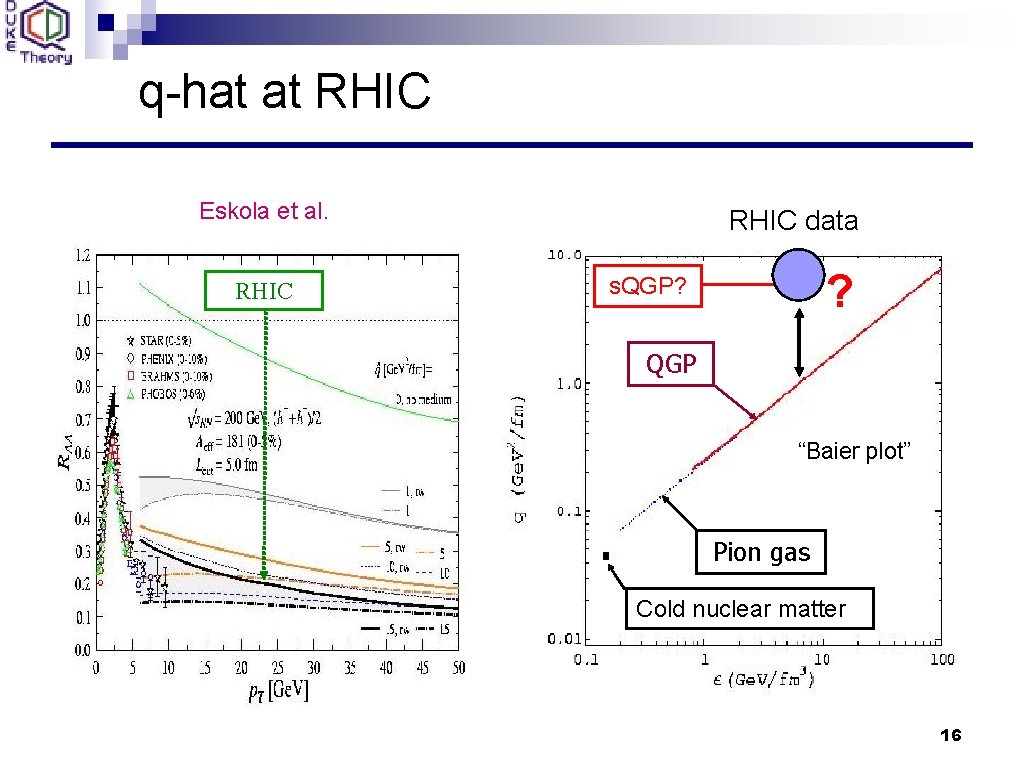
q-hat at RHIC Eskola et al. RHIC data ? s. QGP? QGP “Baier plot” Pion gas Cold nuclear matter 16

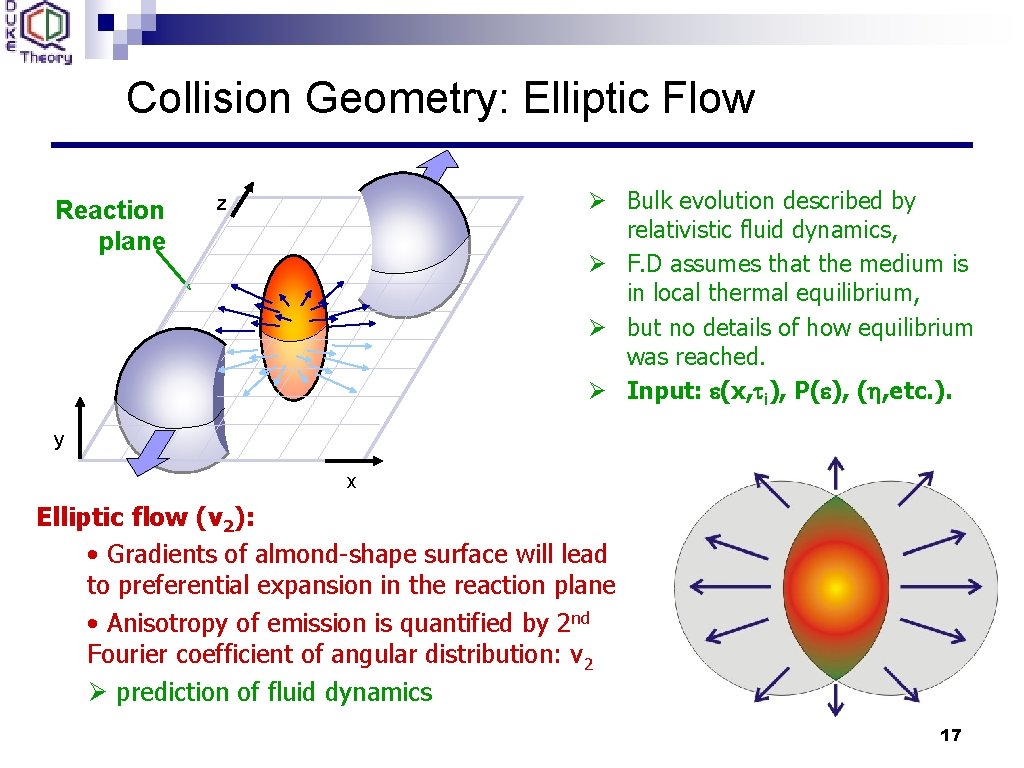
Collision Geometry: Elliptic Flow Reaction plane Ø Bulk evolution described by relativistic fluid dynamics, Ø F. D assumes that the medium is in local thermal equilibrium, Ø but no details of how equilibrium was reached. Ø Input: e(x, ti), P(e), (h, etc. ). z y x Elliptic flow (v 2): • Gradients of almond-shape surface will lead to preferential expansion in the reaction plane • Anisotropy of emission is quantified by 2 nd Fourier coefficient of angular distribution: v 2 Ø prediction of fluid dynamics 17

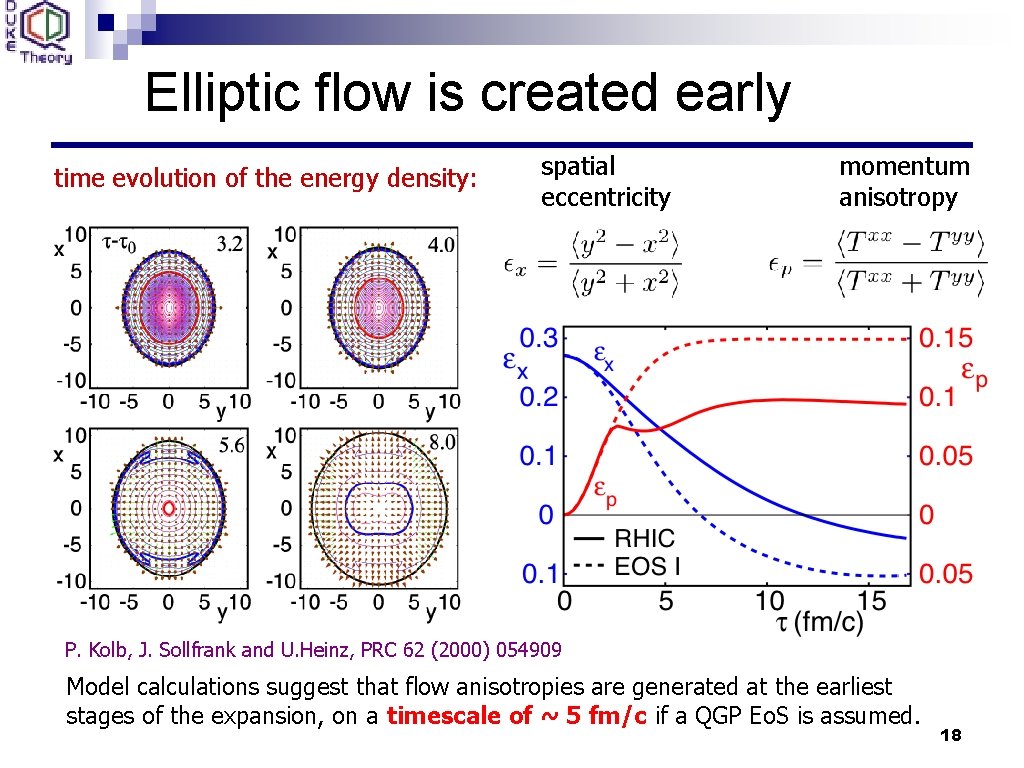
Elliptic flow is created early time evolution of the energy density: initial energy density distribution: spatial eccentricity momentum anisotropy P. Kolb, J. Sollfrank and U. Heinz, PRC 62 (2000) 054909 Model calculations suggest that flow anisotropies are generated at the earliest stages of the expansion, on a timescale of ~ 5 fm/c if a QGP Eo. S is assumed. 18

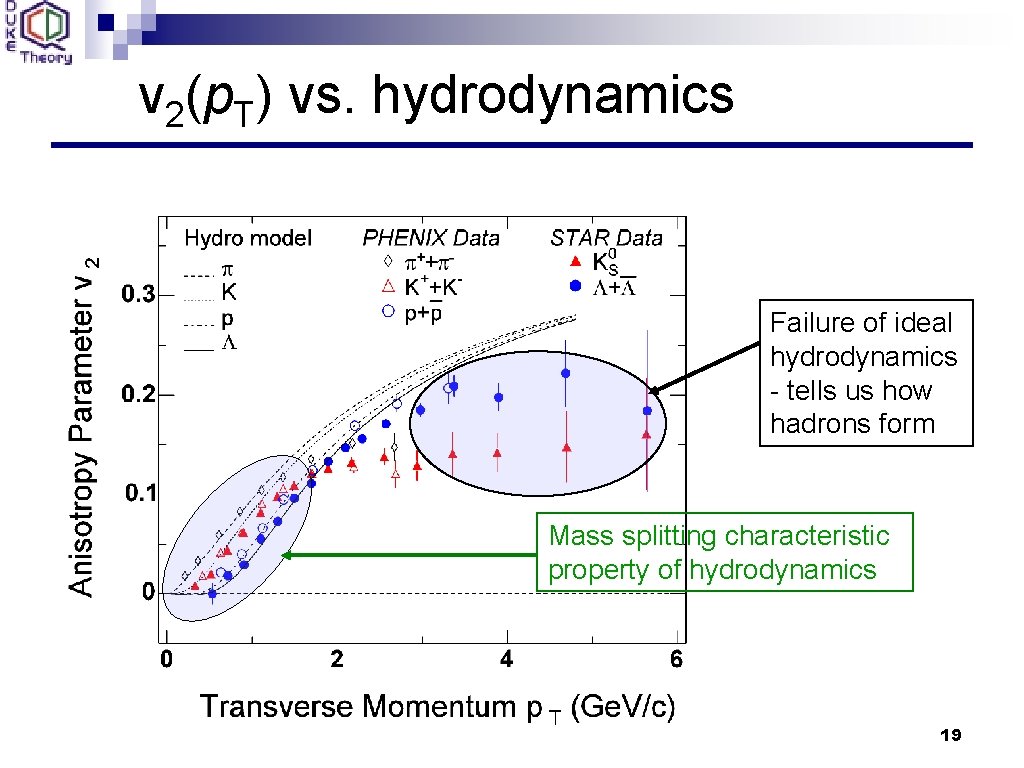
v 2(p. T) vs. hydrodynamics Failure of ideal hydrodynamics - tells us how hadrons form Mass splitting characteristic property of hydrodynamics 19

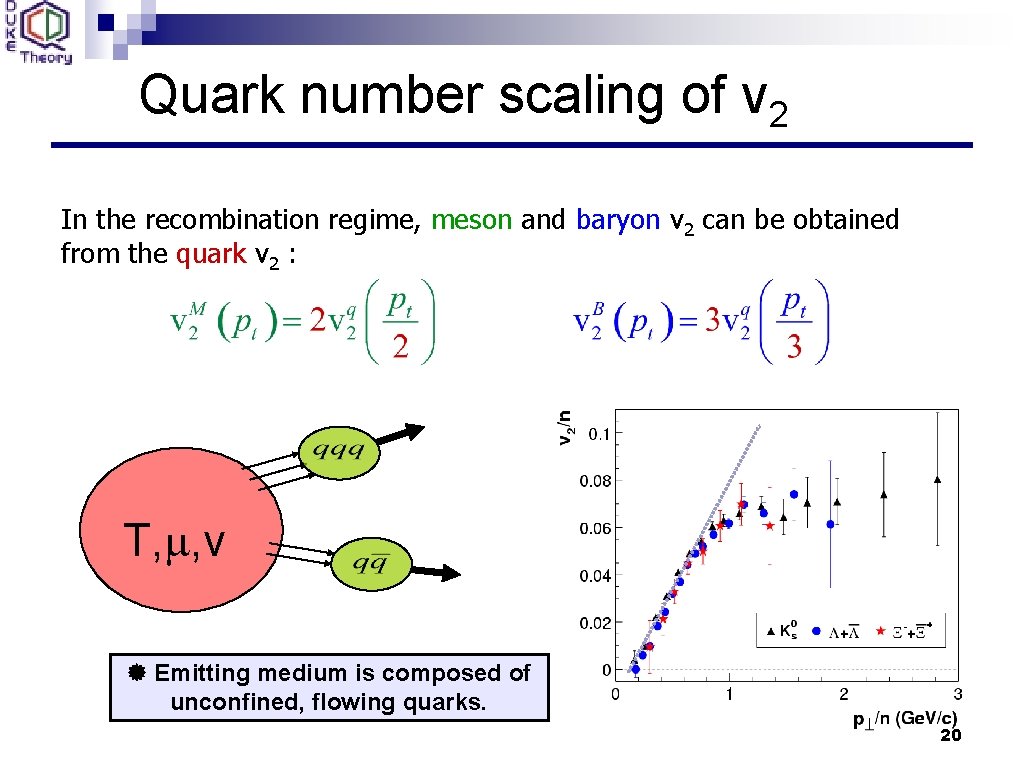
Quark number scaling of v 2 In the recombination regime, meson and baryon v 2 can be obtained from the quark v 2 : T, m, v Emitting medium is composed of unconfined, flowing quarks. 20

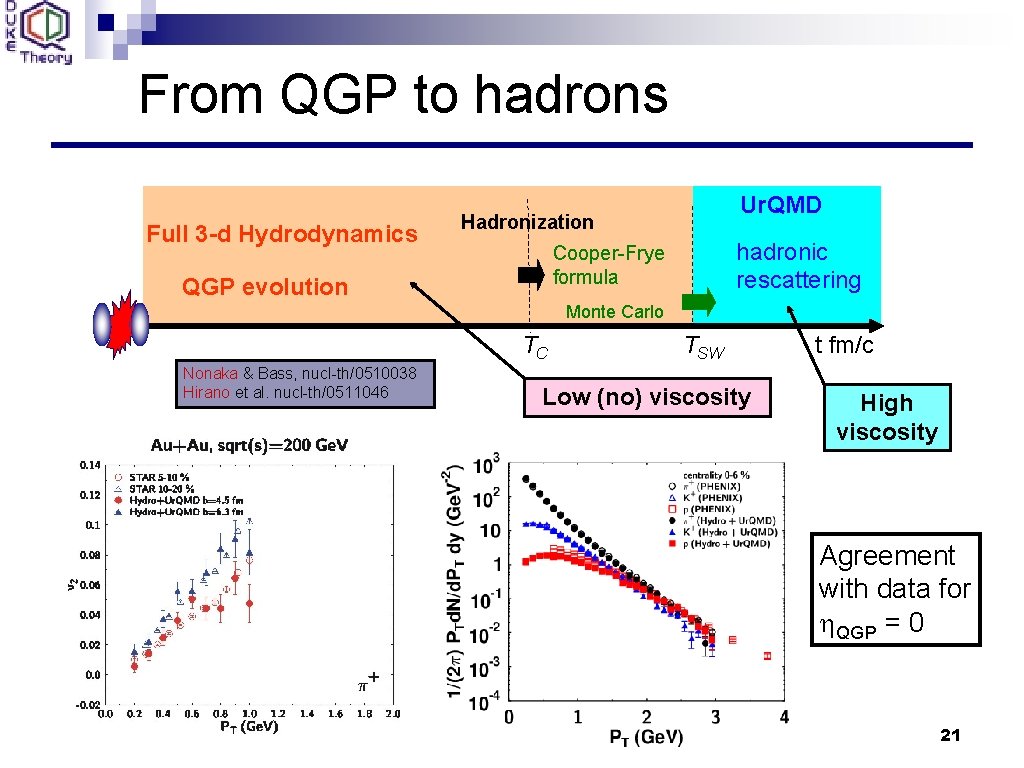
From QGP to hadrons Full 3 -d Hydrodynamics Ur. QMD Hadronization hadronic rescattering Cooper-Frye formula QGP evolution Monte Carlo TC Nonaka & Bass, nucl-th/0510038 Hirano et al. nucl-th/0511046 TSW Low (no) viscosity t fm/c High viscosity Agreement with data for h. QGP = 0 21

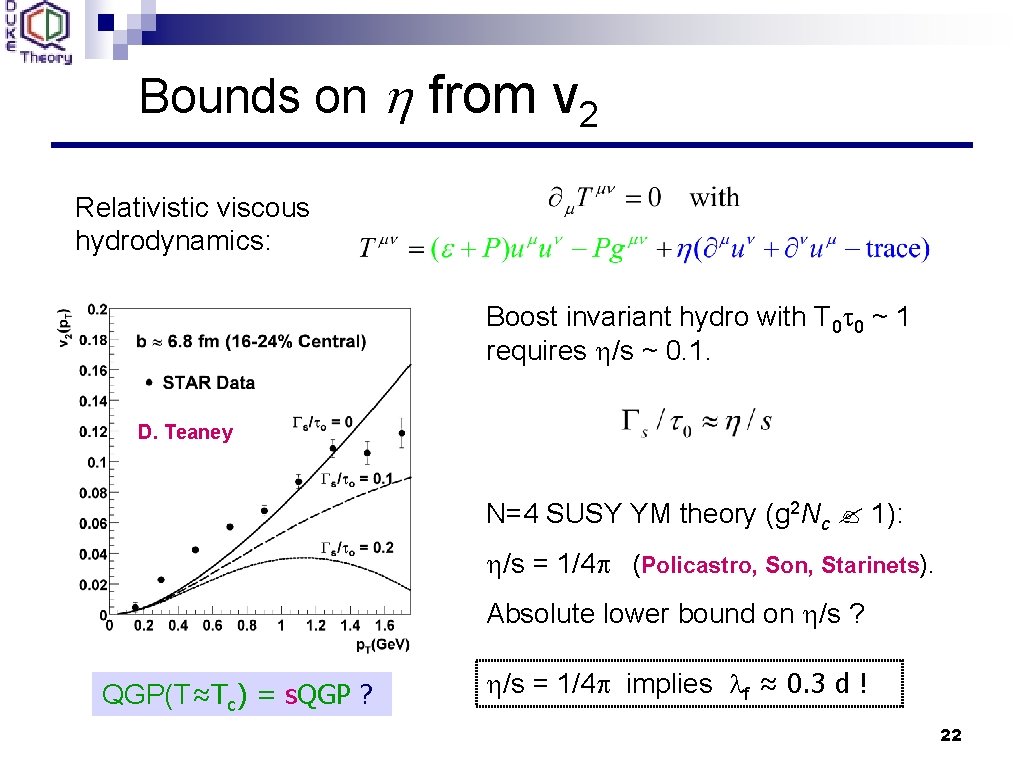
Bounds on h from v 2 Relativistic viscous hydrodynamics: Boost invariant hydro with T 0 t 0 ~ 1 requires h/s ~ 0. 1. D. Teaney N=4 SUSY YM theory (g 2 Nc 1): h/s = 1/4 p (Policastro, Son, Starinets). Absolute lower bound on h/s ? QGP(T≈Tc) = s. QGP ? h/s = 1/4 p implies lf ≈ 0. 3 d ! 22

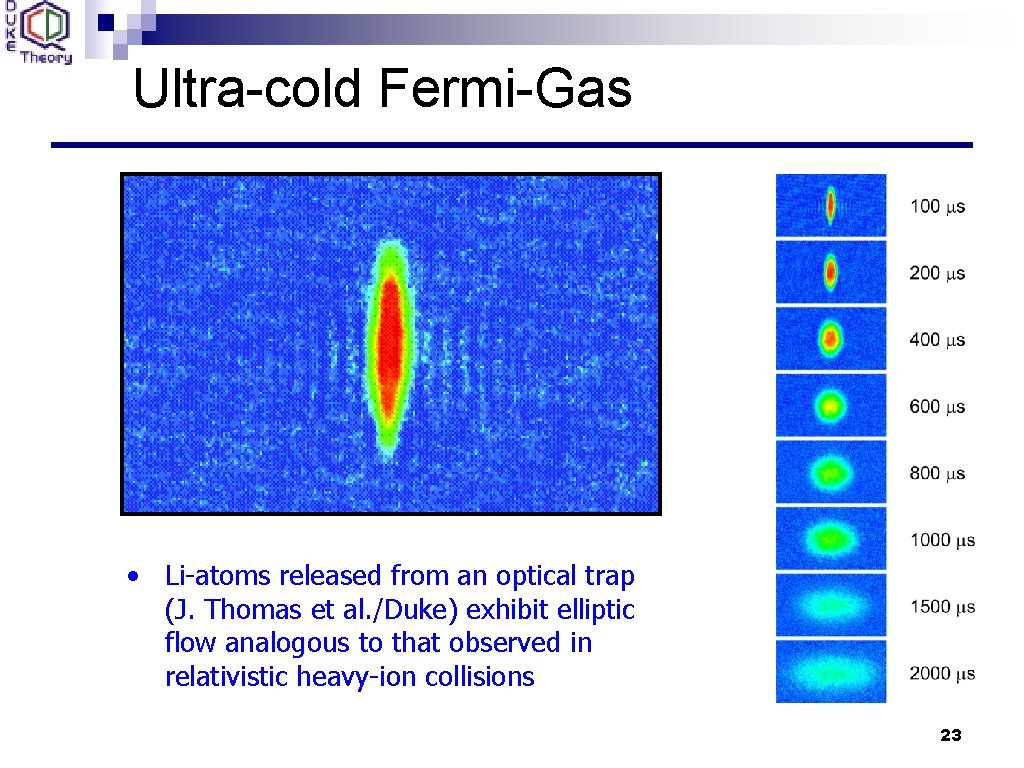
Ultra-cold Fermi-Gas • Li-atoms released from an optical trap (J. Thomas et al. /Duke) exhibit elliptic flow analogous to that observed in relativistic heavy-ion collisions 23

What is an “ideal” or “perfect” liquid ? 24

Ideal gas vs. perfect liquid n An ideal gas is one that has strong enough interactions to reach thermal equilibrium (on a reasonable time scale), but weak enough interactions so that their effect on P(n, T) can be neglected. ¨ n This ideal can be approached arbitraily by diluting the gas and waiting very patiently (limit t first, then V ). A perfect fluid is one that obeys the Euler equations, i. e. a fluid that has zero viscosity and infinite thermal conductivity. There is no presumption with regard to the equation of state. ¨ Even an imperfect fluid obeys the Euler equations in the limit of negligible velocity, density, and temperature gradients. ¨ 25

What is viscosity ? 26

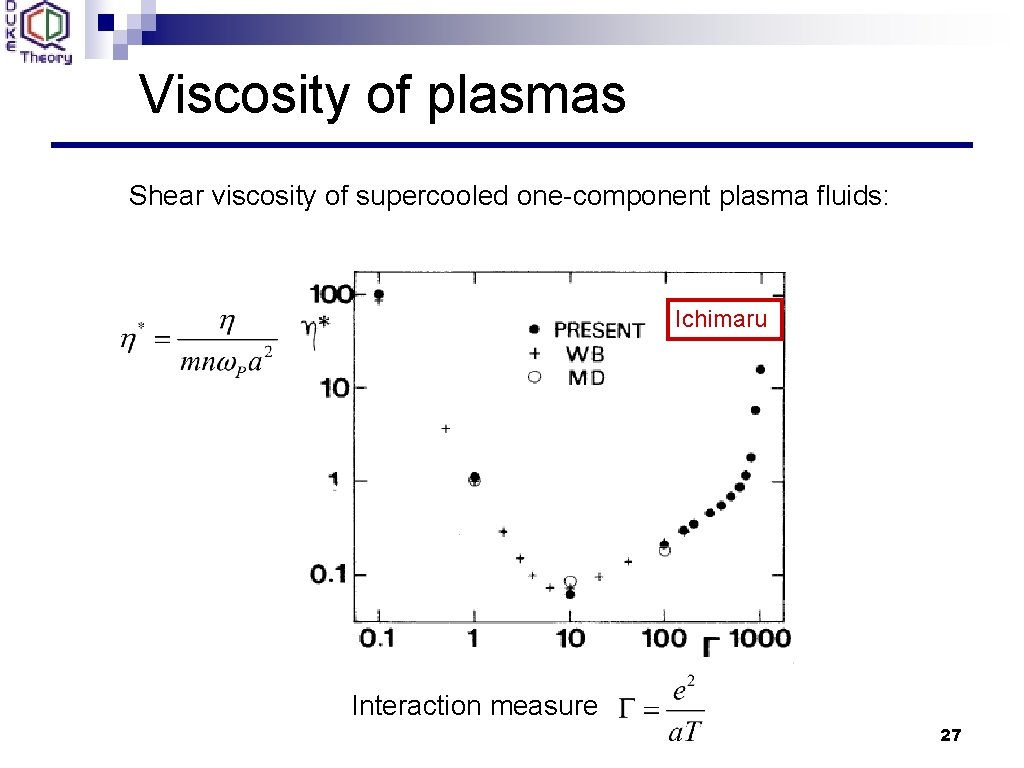
Viscosity of plasmas Shear viscosity of supercooled one-component plasma fluids: Ichimaru Interaction measure 27

Lower bound on h/s ? Argument [Kovtun, Son & Starinets, PRL 94 (2005) 111601] based on duality between thermal QFT and string theory on curved background with D-dimensional black-brane metric, e. g. : Kubo formula for shear viscosity: Dominated by absorption of (thermal) gravitons by the black hole: 28

Lower bound on h/s – ctd. A heuristic argument for (h/s)min is obtained using s ~ 4 n : But the uncertainty relation dictates that tf (e/n) , and thus: (It is unclear whether this relation holds in the nonrelativistic domain, where s/n can be much larger than 4. But is obeyed by all known substances. ) For N=4 susy SU(Nc) Yang-Mills the bound is saturated at strong coupling: 29

Exploring strong coupling n Ability to perform analytical strong coupling calculations in N=4 susy SU(Nc) YM and success with h have motivated other applications: ¨ ¨ ¨ ¨ Equation of state [Gubser, Klebanov, Tseytlin, hep-th/9805156] Spectral densities [Teaney, hep-ph/0602044] Jet quenching parameter [Liu, Rajagopal, Wiedemann, hep-ph/0605178] Heavy quark energy loss [Herzog, Karch, Kovtun, Kozcaz, Yaffe, hepth/0605158] Heavy quark diffusion [Casalderrey-Solana, Teaney, hep-ph/0605199] Drag force on heavy quark [Gubser, hep-th/0605182 ] …and continuing! 30

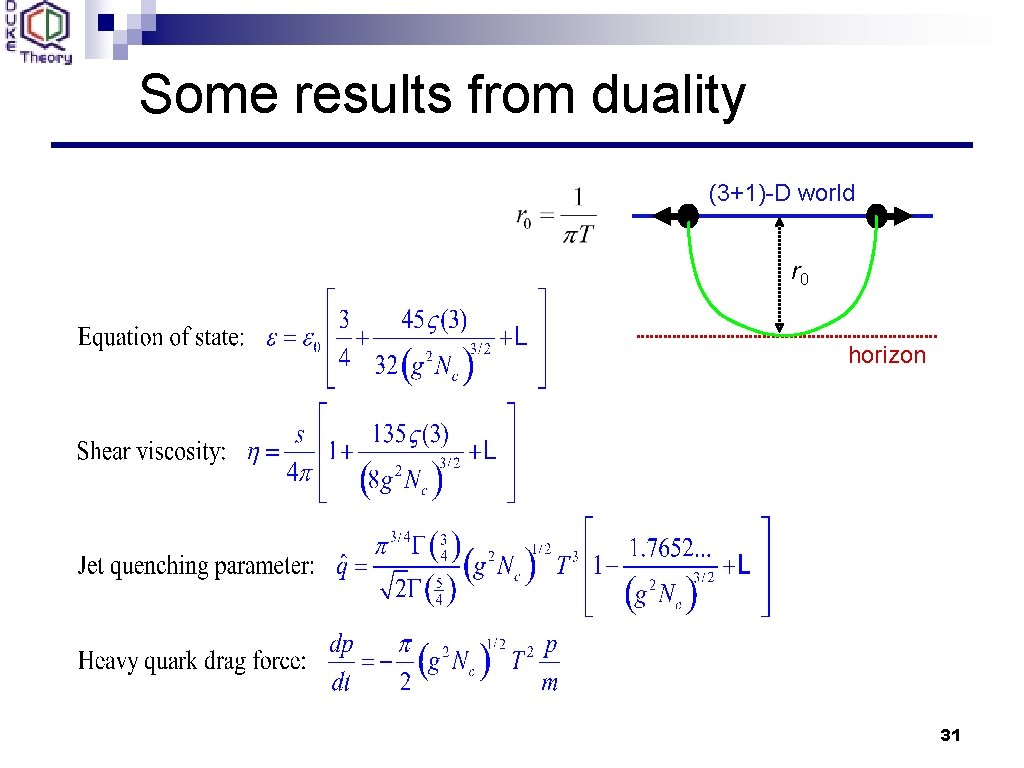
Some results from duality (3+1)-D world r 0 horizon 31

Lecture II n Does “perfect” fluidity imply “strong coupling” ? n What is “anomalous” viscosity ? n Derivation of the anomalous viscosity n Manifestations of anomalous QGP transport processes 32

Today… …we ask the question: Is strong coupling really necessary for small h/s ? 33

What is viscosity ? 34

Stellar accretion disks “A complete theory of accretion disks requires a knowledge of the viscosity. Unfortunately, viscous transport processes are not well understood. Molecular viscosity is so small that disk evolution due to this mechanism of angular momentum transport would be far too slow to be of interest. If the only source of viscosity was molecular, then n ~ h/r ~ l v. T, where l is the particle mean free path and v. T is thermal velocity. Values appropriate for a disk around a newly formed star might be r ~ 1014 cm, n ~ 1015 cm-3, s ~ 10 -16 cm 2, so that l ~ 10 cm, and v. T ~ 105 cm/s. The viscous accretion time scale would then be r 2/(12 n) > 1013 yr! Longer by a factor of 105 - 106 than the age conventionally ascribed to such disks. Clearly if viscous accretion explains such objects, there must be an anomalous source of viscosity. The same conclusion holds for all the other astronomical objects for which the action of accretion disks have been invoked. ” (From James Graham – Astronomy 202, UC Berkeley) http: //grus. berkeley. edu/~jrg/ay 202/lectures. html The solution is: String theory? Unfortunately, NO. 35

Anomalous viscosity B Differentially rotating disc with weak magnetic field B shows an instability (Chandrasekhar) “Anomalous”, i. e. non-collisional viscosity Spontaneous angular momentum transfer from inner mass to outer mass is amplified by interaction with the rotating disk and leads to instability (Balbus & Hawley – 1991). 36

Anomalous viscosity: A ubiquitous phenomenon 37

Anomalous viscosity on the WWW Google search: Results 1 - 10 of about 322, 000 for anomalous viscosity. (0. 22 seconds) Chaotic Dynamics, abstract chao-dyn/9509002 Anomalous Viscosity, Resistivity, and Thermal Diffusivity of the Solar Wind Plasma Authors: Mahendra K. Verma (IIT Kanpur, India) In this paper we have estimated typical anomalous viscosity, resistivity, and thermal difffusivity of the solar wind plasma. Since the solar wind is collsionless plasma, we have assumed that the dissipation in the solar wind occurs at proton gyro radius through wave-particle interactions. Using this dissipation length-scale and the dissipation rates calculated using MHD turbulence phenomenology [Verma et al. , 1995 a], we estimate the viscosity and proton thermal diffusivity. The resistivity and electron's thermal diffusivity have also been estimated. We find that all our transport quantities are several orders of magnitude higher than those calculated earlier using classical transport theories of Braginskii. In this paper we have also estimated the eddy turbulent viscosity. 38

Anomalous viscosity - origins 39

Anomalous viscosity - usage n Plasma physics: ¨ n Astrophysics - dynamics of accretion disks: ¨ n A. V. = large viscosity induced in nearly collisionless plasmas by long-range fields generated by plasma instabilities. A. V. = large viscosity induced in weakly magnetized, ionized stellar accretion disks by orbital instabilities. Biophysics: ¨ A. V. = The viscous behaviour of nonhomogenous fluids or suspensions, e. g. , blood, in which the apparent viscosity increases as flow or shear rate decreases toward zero. (From: http: //www. biology-online. org/dictionary) 40

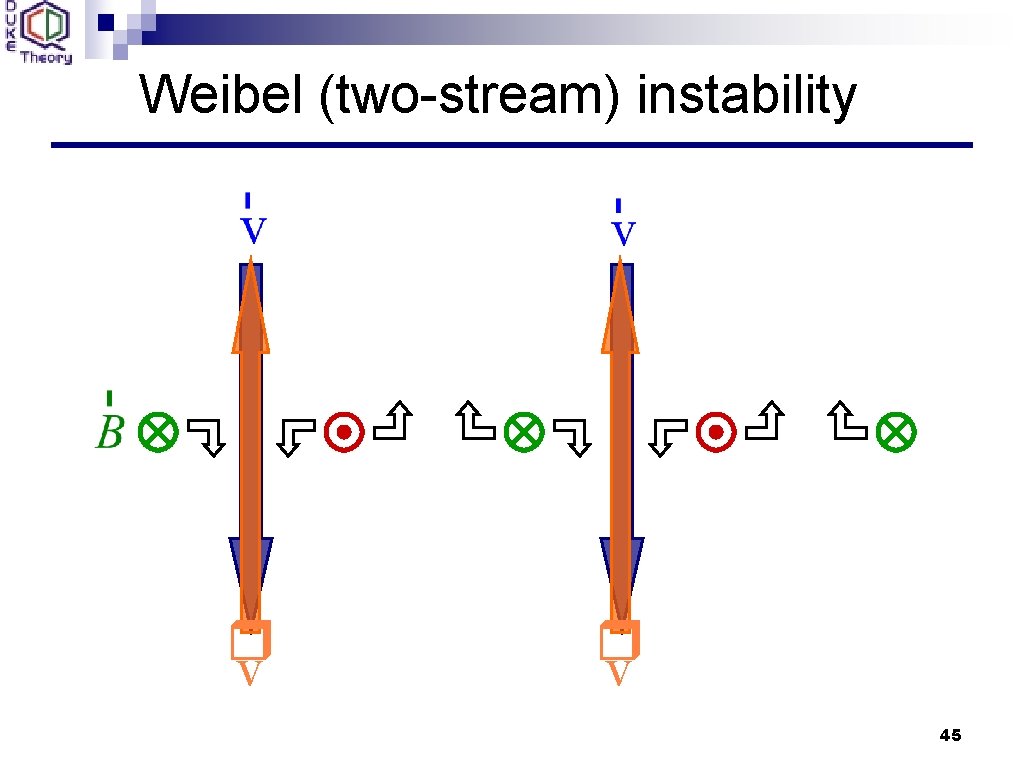
Can the QGP viscosity be anomalous? n Can the extreme opaqueness of the QGP (seen in experiments) be explained without invoking super-strong coupling ? n Answer may lie in the peculiar properties of turbulent plasmas. n Plasma “turbulence” = random, nonthermal excitation of coherent field modes with power spectrum similar to the vorticity spectrum in a turbulent fluid [P(k) ~ 1/k 2]. n Plasma turbulence arises naturally in plasmas with an anisotropic momentum distribution (Weibel-type instabilities). n Expanding plasmas (such as the QGP at RHIC) always have anisotropic momentum distributions. n Soft color fields generate anomalous transport coefficients, which may give the medium the character of a nearly perfect fluid even at moderately weak coupling. 41

QGP viscosity – collisions Baym, Heiselberg, …. Danielewicz & Gyulassy, Phys. Rev. D 31, 53 (85) 42

QGP viscosity – anomalous 43

Color instabilities Spontaneous generation of color fields requires infrared instabilities. Unstable modes in plasmas occur generally when the momentum distribution of a plasma is anisotropic (Weibel instabilities – 1959). Such conditions are satisfied in HI collisions: py Longitudinal expansion locally “red-shifts” the longitudinal momentum components of released small-x gluon fields (CGC) from initial state: px beam pz In EM case, instabilities saturate due to effect on charged particles. In YM case, field nonlinearities lead to saturation (competition with Nielsen-Olesen instability? ) 44

Weibel (two-stream) instability r v 45

HTL formalism Nonabelian Vlasov equations describe interaction of “hard” and “soft” color field modes and generate the “hard-thermal loop” effective theory: “soft” “hard” k ~ g. T (g. Qs) k ~ T (Qs) Effective HTL theory permits systematic study of instabilities of “soft” color fields. 46

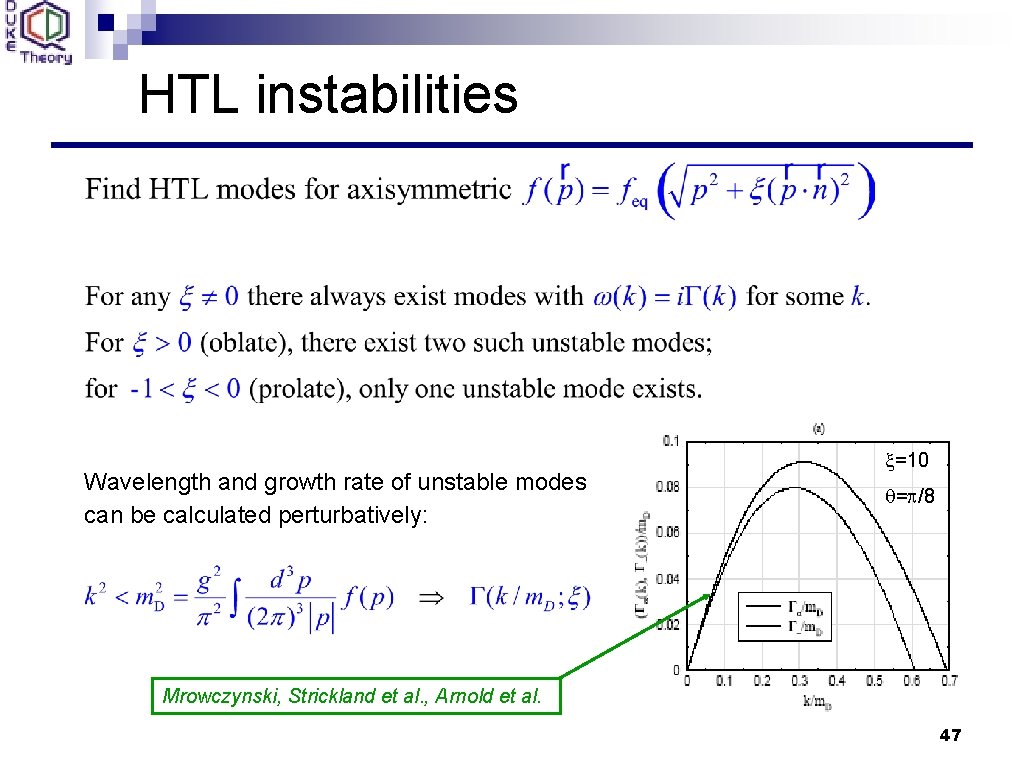
HTL instabilities Wavelength and growth rate of unstable modes can be calculated perturbatively: x=10 q=p/8 Mrowczynski, Strickland et al. , Arnold et al. 47

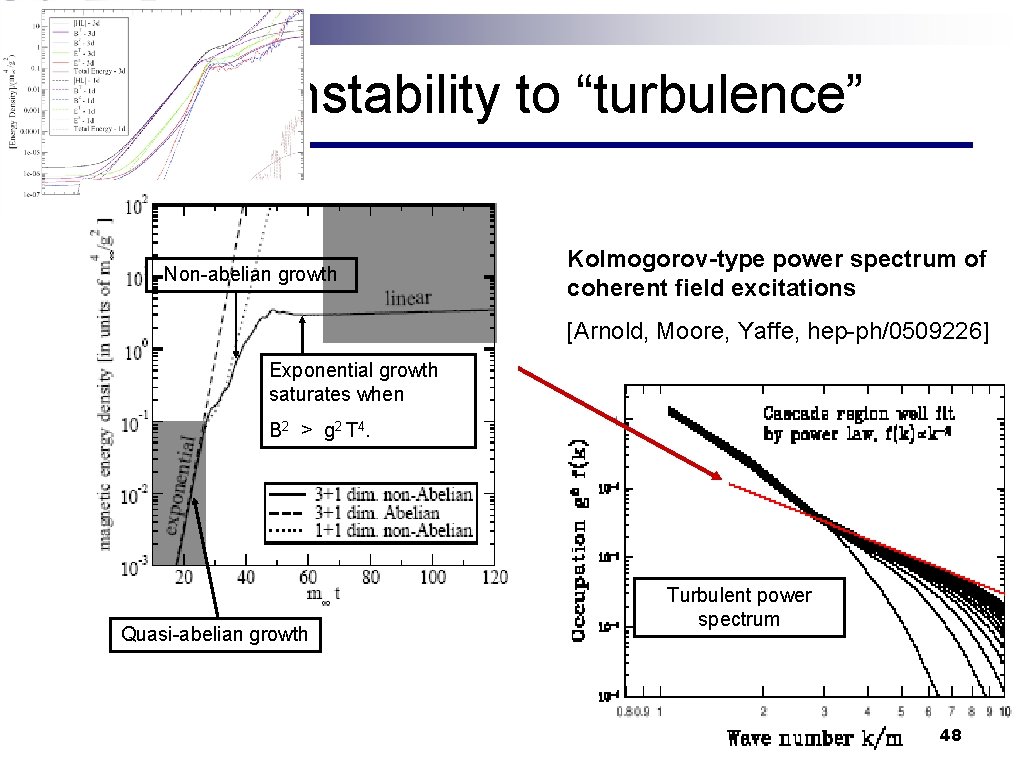
From instability to “turbulence” Non-abelian growth Kolmogorov-type power spectrum of coherent field excitations [Arnold, Moore, Yaffe, hep-ph/0509226] Exponential growth saturates when B 2 > g 2 T 4. Quasi-abelian growth Turbulent power spectrum 48

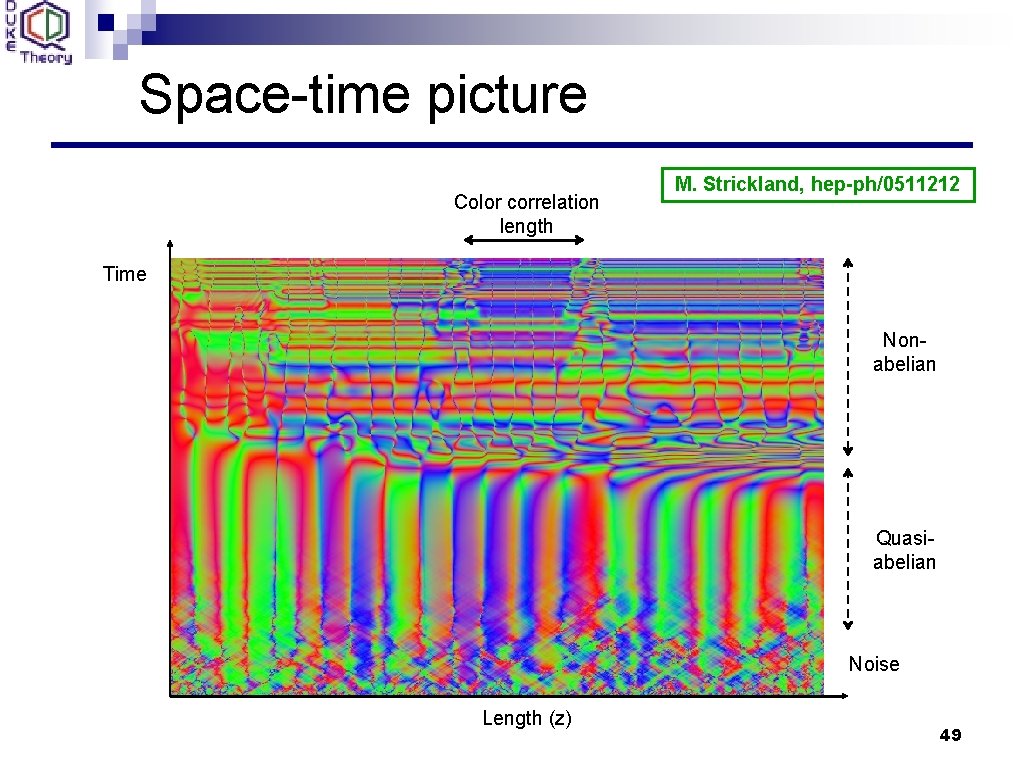
Space-time picture Color correlation length M. Strickland, hep-ph/0511212 Time Nonabelian Quasiabelian Noise Length (z) 49

Anomalous viscosity Formal derivation (Sorry – using Chapman-Enskog) 50

Expansion Anisotropy QGP X-space QGP P-space Anisotropic momentum distributions generate instabilities of soft field modes. Growth rate G ~ f 1(p). Shear flow always results in the formation of soft color fields; Size controlled by f 1(p), i. e. ( u) and h/s. 51

Turbulence Diffusion 52

Shear viscosity Take moments of with pz 2 M. Asakawa, S. A. Bass, B. M. , hep-ph/0603092 See Abe & Niu (1980) for effect in EM plasmas 53

ηA - the feedback loop • Longitudinal flow induces momentum anisotropy: p pz Ø Anisotropy grows with shear viscosity _η • Soft color fields are proportional to Δ: • The anomalous viscosity is inversely proportional to B 2 : Self-consistency • Shear viscosity η stabilizes due to: 54

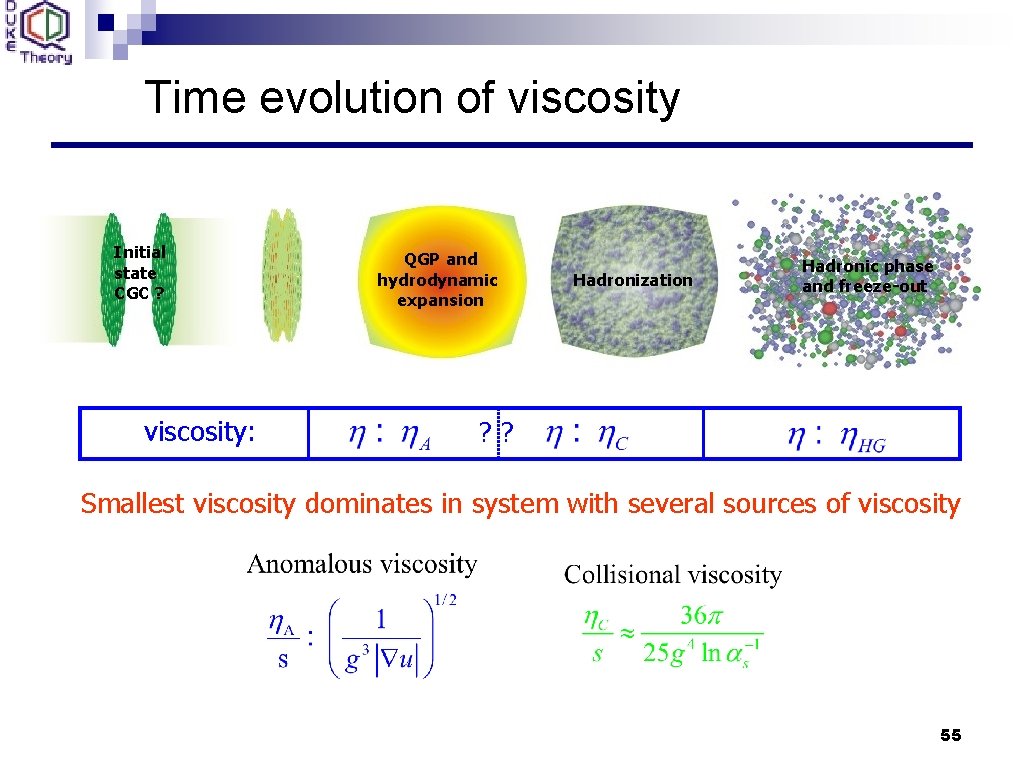
Time evolution of viscosity Initial state CGC ? viscosity: QGP and hydrodynamic expansion Hadronization Hadronic phase and freeze-out ? ? Smallest viscosity dominates in system with several sources of viscosity 55

Manifestations? n Possible effects on QGP probes: ¨ ¨ Longitudinal broadening of jet cones (observed – “ridge”) Anomalous diffusion of charm and bottom quarks (observed) Jet B x y z Synchrotron-style radiation of soft, nonthermal photons ? Au+Au 20 -30% Field induced quarkonium dissociation ? b a c ¨ No unstable modes for quarks: quasi -particle picture of QGP is compatible with low viscosity c b 56

Summary Conclusion: Because the matter created in heavy ion collisions expands rapidly, it forms a turbulent color plasma, which has an anomalously small shear viscosity. Transport phenomena involving quarks and gluons are strongly influenced by the turbulent color fields, especially at early times, when the expansion is rapid. 57

Additional slides 58

Anisotropic HTL modes 59

Shear perturbation 60

Estimate of h. A 61

Turbulence Diffusion 62

Shear viscosity hep-ph/0603092 PRL (June 30) 63

Diffusion Viscosity Diffusion corresponds to “anomalous” viscosity: But recall that B 2 itself depends on anisotropy f 1(p) ~ viscosity h ! 64

ηB - the feedback loop • Longitudinal flow induces momentum anisotropy: p pz Ø Anisotropy grows with shear viscosity _η • Soft color fields are proportional to Δ: The Münchhausen effect • The anomalous viscosity is inversely proportional to B 2 : • Shear viscosity η stabilizes due to: 65

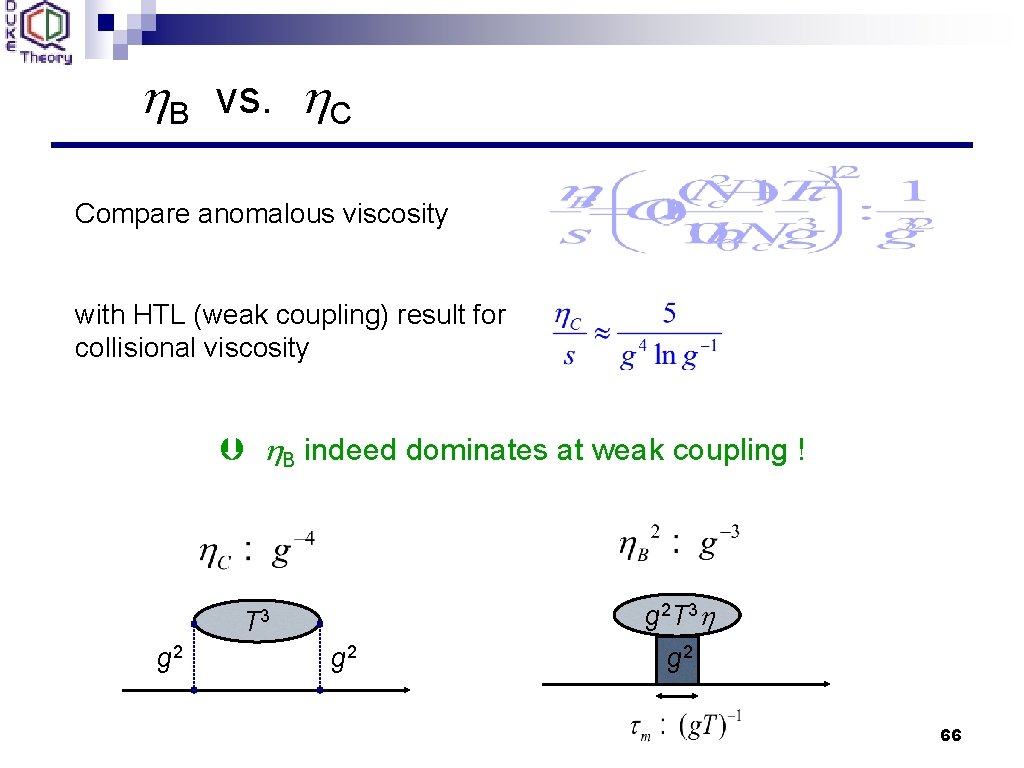
h. B vs. h. C Compare anomalous viscosity with HTL (weak coupling) result for collisional viscosity h. B indeed dominates at weak coupling ! T 3 g 2 g 2 T 3 h g 2 66