Why do we study algorithms 2 First results

Why do we study algorithms?

2

First results are about bats and dolphins

Algorithmics: the Spirit of Computing • As per David Harel (A writer on Algorithms) • Algorithmics is more than a branch of computer science. It is the core of computer science, and, in all fairness, can be said to be relevant to most of science, business, and technology. [Har 92, p. 6] 4

Donald Knuth, one of the most prominent computer scientists in the history of algorithmics, put it as follows: A person well-trained in computer science knows how to deal with algorithms: how to construct them, manipulate them, understand them, analyze them. This knowledge is preparation for much more than writing good computer programs; it is a general-purpose mental tool that will be a definite aid to the understanding of other subjects, whether they be chemistry, linguistics, or music, etc. The reason for this may be understood in the following way: It has often been said that a person does not really understand something until after teaching it to someone else. Actually, a person does not really understand something until after teaching it to a computer, i. e. , expressing it as an algorithm. . . An attempt to formalize things as algorithms leads to a much deeper understanding than if we simply try to comprehend things in the traditional way. [Knu 96, p. 9] 5

Main Topics Covered • • • • Introduction to the course and the course objectives Why Algorithm Analysis Techniques and Basic Mathematics Recurrence Divide and Conquer algorithm design strategy Sorting in linear time String Matching Dynamic Programming algorithm design strategy Greedy algorithms Backtracking Branch & Bound Graph Algorithms Guided Study of the state of art algorithms from the research papers 6

Algorithm • an algorithm is a finite sequence of unambiguous instructions to perform a specific task • An algorithm has a name, begins with a precisely specified input, and terminates with a precisely specified output • Input and output are finite sequences of mathematical objects

Correct Algorithm • An algorithm is said to be correct if given input as described in the input specifications: 1. the algorithm terminates in a finite time; 2. on termination the algorithm returns output as described in the output specifications.

At least three important questions need to be answered for each algorithm • Is it correct? • How much time and space does it take, as a function of n? • And can we do better? Being problem solvers, we need to equip ourselves with the tools and techniques to answer these questions. We will first focus on point 2. 9

• Time efficiency, also called time complexity, indicates how fast an algorithm in question runs • Space efficiency, also called space complexity, refers to the amount of memory units required by the algorithm in addition to the space needed for its input and output 10

An Example Consider the problem of sorting numbers INPUT: Sequence of n numbers <a 1, a 2, a 3, …. an> OUTPUT: Permutation (reordering) <a 1`, a 2`, a 3`, …. an`> of the input sequence such that a 1`<a 2`<a 3`<…. . <an` Many algorithms are available. 11

An algorithm for sorting. Get a list of unsorted numbers Set a marker for the unsorted section at the front of the list Repeat steps 4 - 6 until one number remains in the unsorted section Compare all unsorted numbers in order to select the smallest one Swap this number with the first number in the unsorted section Advance the marker to the right one position Stop 12

Another algorithm for sorting Divide sequence of m elements into two sequences of m/2 elements Conquer both sub-sequences using Merge Sort (recursively) Combine two sorted sub-sequences using merge 13

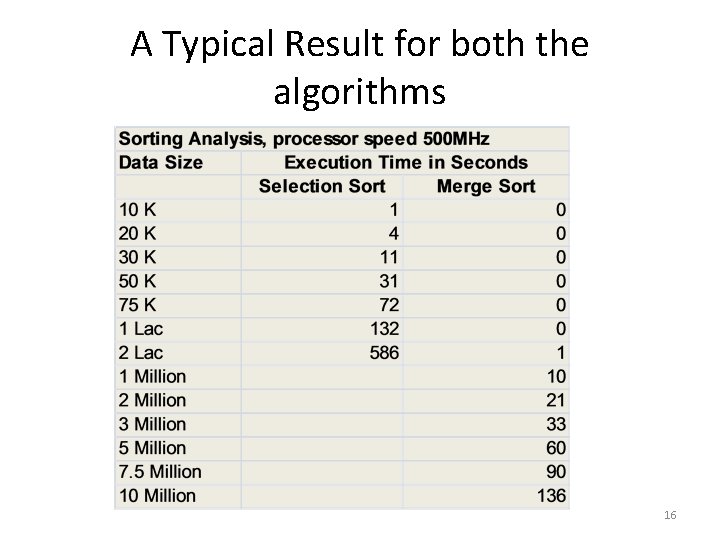
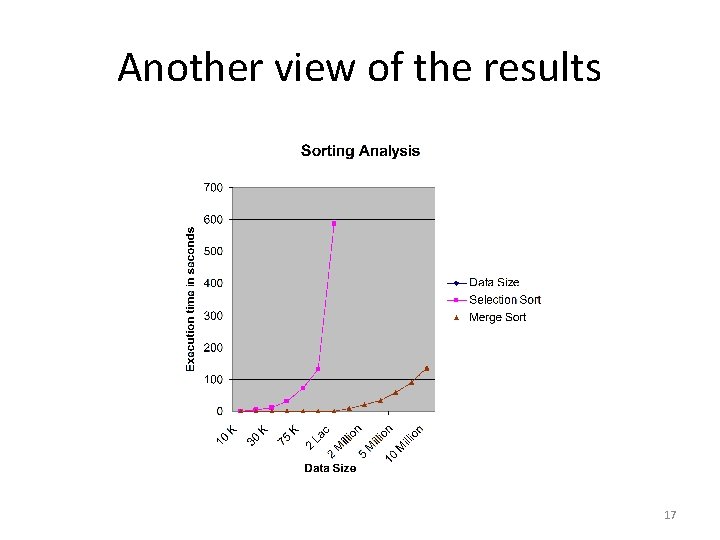
How much time does each algorithm take, as a function of n? Implement both algorithms Note down the execution time for each algorithm Compare the times 14

Possible steps? Understand the problem Formulate a solution / algorithm Analyze the algorithm • • Design a program Implement the program Execute the code Measure the time See if the solution is ok Otherwise try to come up with another solution and again start from step 1 15

A Typical Result for both the algorithms 16

Another view of the results 17

• How to analyze an algorithm with minimum effort? • Predict the resources that the algorithm requires –Memory –Communications Bandwidth –Logic gates etc –Most important is Computational Time 18

Possible steps with minimum effort? 1. Understand the problem 2. Formulate a solution / algorithm 3. Analyze the algorithm a) b) c) d) Design a program Implement the program Execute the code Measure the time 4. See if the solution is ok 5. Otherwise try to come up with another solution and again start from step 1 19

• Important things before analysis – Model of the machine upon which the algorithms is executed. – Random Access Machine (RAM) (Sequential) to start with • Running Time: – No. of primitive operations or “steps executed”. 20

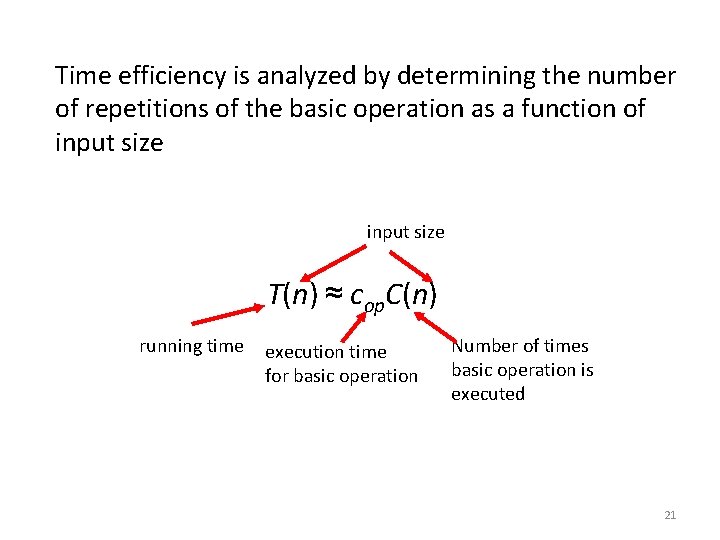
Time efficiency is analyzed by determining the number of repetitions of the basic operation as a function of input size T(n) ≈ cop. C(n) running time execution time for basic operation Number of times basic operation is executed 21

• How do we write algorithms? • Pseudo Code: – Similar construct / keywords as in a high level programming languages, e. g. in C, Pascal etc. – Structured semantics of the high level languages without caring about the syntactic errors / grammatical rules 22

The language of algorithms Algorithm h algorithm name i INPUT: h input specification i OUTPUT: h output specification i <statement >; . . . <statement >; end;

Sample Pseudo Code Max-Subsequence-Sum(Array, N) { } //Where N is size of Array int this-sum = 0, Max-sum = 0; for(int i = 0; i < N; i++) { for(int j = i; j < N; j++) { this-sum = 0; for(int k = i; k <= j; k++) this-sum = this-sum + Array[k]; if(this-sum > Max-sum) Max-sum = this-sum; } } return(Max-sum);

How much time each construct / keyword of a pseudo code takes to execute. Assume it takes ti (the ith construct) Sum / Add up the execution time of all the constructs / keywords. if there are m constructs then total time for all the constructs is 25

• That will be the execution time for a given input size (say n) • Running time as the function of the input size T(n) 26

• • What are the constructs / Keywords. Time for each construct Total Time Total time as a function of input size 27

• Constructs: 1. Sequence 2. Selection 3. Iterations 4. Recursion 28

• Sequence Statements: – Just add the running time of the statements • Iteration is at most the running time of the statements inside the loop (including tests) times the number of iterations. 29

Example 1 • Analyze Time for the following algorithm – Find the value of the largest element in a list of n numbers. Max. Element(A[0. . n-1) max. Val = A[0]; for(I = 1; I < n; I++) if(A[I] > max. Val) max. Val = A[I]; return max. Val 30

• If-Then-Else: – if (condition) S 1 else S 2 – Running time of the test plus the larger of the running times of S 1 and S 2. • Nested Loops: Analyze these inside out. The total Running time of a statement inside a group of nested loops is the running time of the statement multiplied by the product of the size of all the loops. • Function Calls: Analyzing from inside to out. If there are function calls, these must be analyzed first. 31

Example 2 • Check whether all the elements in a given array are distinct. Unique. Elements(A[0. . n-1]) for(I = 0; i<n-1; i++) for(j = i+1; j<n; j++) if(A[i] = A[j]) return false return true 32

Useful Formulas for the Analysis of Algorithms aqadir@jinnah. edu. pk 33

34

35

Analysis Example Max-Subsequence-Sum(Array, N) { } //Where N is size of Array int this-sum = 0, Max-sum = 0; for(int i = 0; i < N; i++) { for(int j = i; j < N; j++) { this-sum = 0; for(int k = i; k <= j; k++) this-sum = this-sum + Array[k]; if(this-sum > Max-sum) Max-sum = this-sum; } } return(Max-sum);

Assignment: Analyze the algorithm 1

Assignment: Analyze the algorithm 2

Assignment: Analyze the algorithm 3

Assignment: Analyze the algorithm 4

Assignment: Analyze the algorithm 5

Assignment: Analyze the algorithm 6

Assignment: Analyze the algorithm 7