Why do we care about crystal structures directions

Why do we care about crystal structures, directions, planes ? Physical properties of materials depend on the geometry of crystals ISSUES TO ADDRESS. . . • How do atoms assemble into solid structures? (for now, focus on metals) • How does the density of a material depend on its structure? • When do material properties vary with the sample (i. e. , part) orientation? Chapter 3 - 1

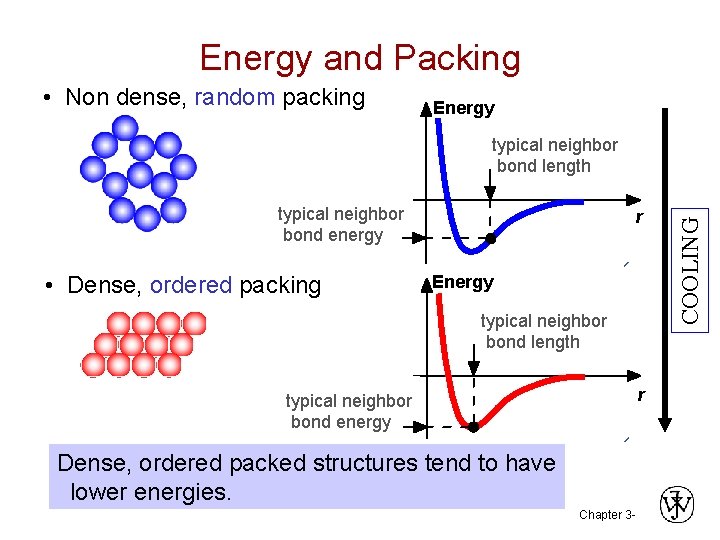
Energy and Packing • Non dense, random packing Energy typical neighbor bond energy • Dense, ordered packing r Energy typical neighbor bond length r typical neighbor bond energy Dense, ordered packed structures tend to have lower energies. Chapter 3 - COOLING typical neighbor bond length

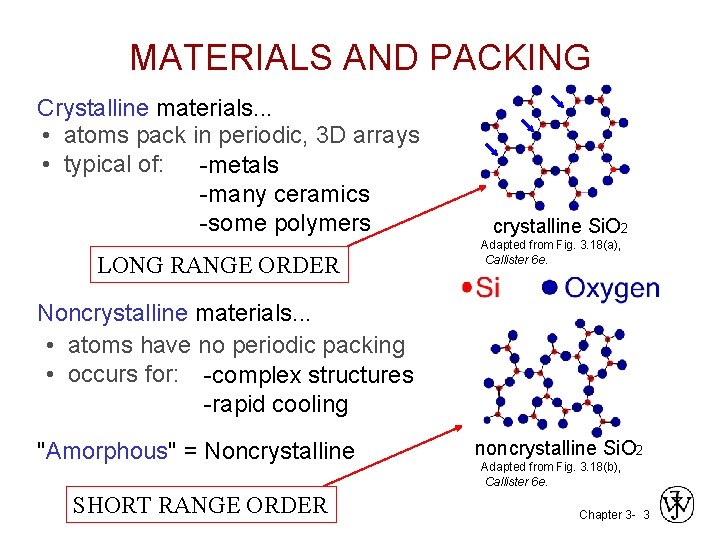
MATERIALS AND PACKING Crystalline materials. . . • atoms pack in periodic, 3 D arrays • typical of: -metals -many ceramics -some polymers LONG RANGE ORDER crystalline Si. O 2 Adapted from Fig. 3. 18(a), Callister 6 e. Noncrystalline materials. . . • atoms have no periodic packing • occurs for: -complex structures -rapid cooling "Amorphous" = Noncrystalline SHORT RANGE ORDER noncrystalline Si. O 2 Adapted from Fig. 3. 18(b), Callister 6 e. Chapter 3 - 3

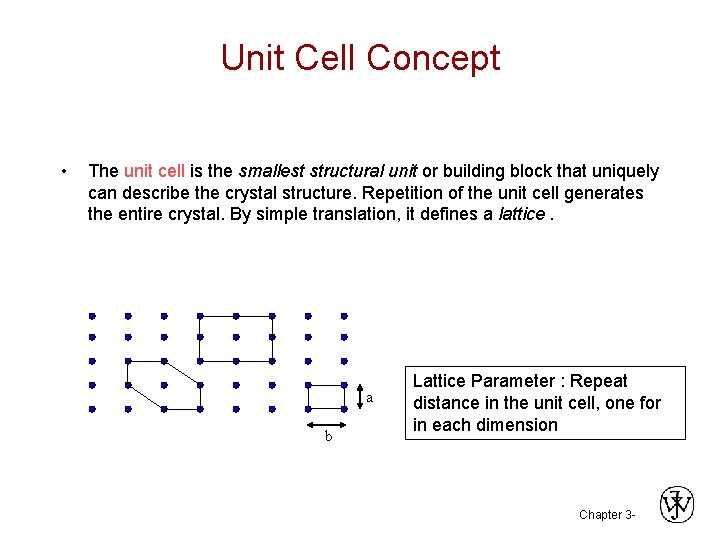
Unit Cell Concept • The unit cell is the smallest structural unit or building block that uniquely can describe the crystal structure. Repetition of the unit cell generates the entire crystal. By simple translation, it defines a lattice. a b Lattice Parameter : Repeat distance in the unit cell, one for in each dimension Chapter 3 -

Crystal Systems • Units cells and lattices in 3 -D: – When translated in each lattice parameter direction, MUST fill 3 -D space such that no gaps, empty spaces left. b a c Lattice Parameter : Repeat distance in the unit cell, one for in each dimension Chapter 3 -

Section 3. 3 – Crystal Systems Unit cell: smallest repetitive volume which contains the complete lattice pattern of a crystal. 7 crystal systems 14 crystal lattices a, b, and c are the lattice constants Fig. 3. 4, Callister 7 e. Chapter 3 -

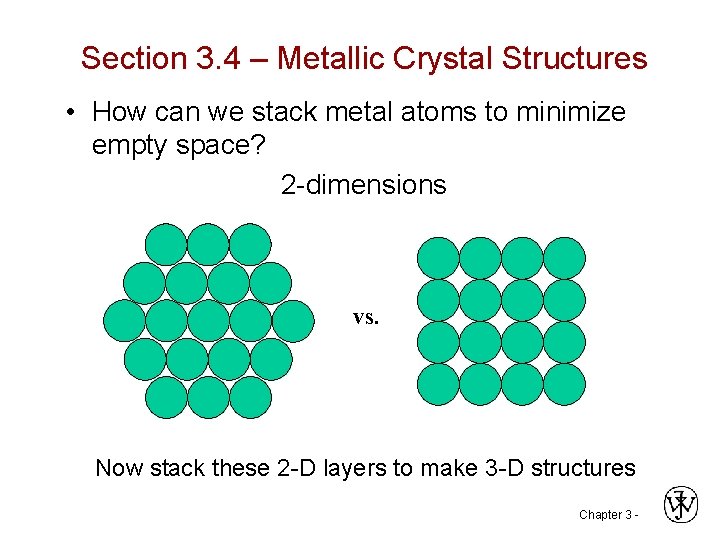
Section 3. 4 – Metallic Crystal Structures • How can we stack metal atoms to minimize empty space? 2 -dimensions vs. Now stack these 2 -D layers to make 3 -D structures Chapter 3 -

METALLIC CRYSTALS • tend to be densely packed. • have several reasons for dense packing: -Typically, only one element is present, so all atomic radii are the same. -Metallic bonding is not directional. -Nearest neighbor distances tend to be small in order to lower bond energy. • have the simplest crystal structures. We will look at three such structures. . . Remember metallic bond => non-directional, does not restrict number of nearest-neighbors ( covalent ; 8 -N’ rule), allows for dense atomic packing Chapter 3 - 4

WEB SITE http: //professor. wiley. com/CGI-BIN/LANSAWEB? PROCFUN+PROF 1+PRFFN 22 Chapter 3 -

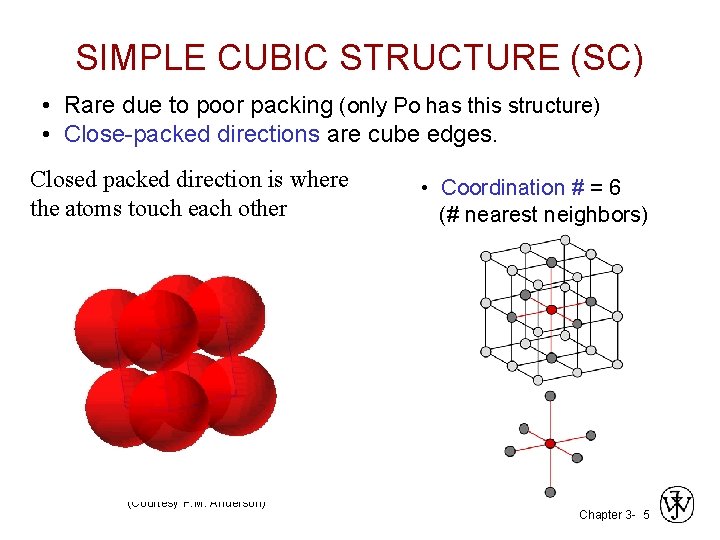
SIMPLE CUBIC STRUCTURE (SC) • Rare due to poor packing (only Po has this structure) • Close-packed directions are cube edges. Closed packed direction is where the atoms touch each other (Courtesy P. M. Anderson) • Coordination # = 6 (# nearest neighbors) Chapter 3 - 5

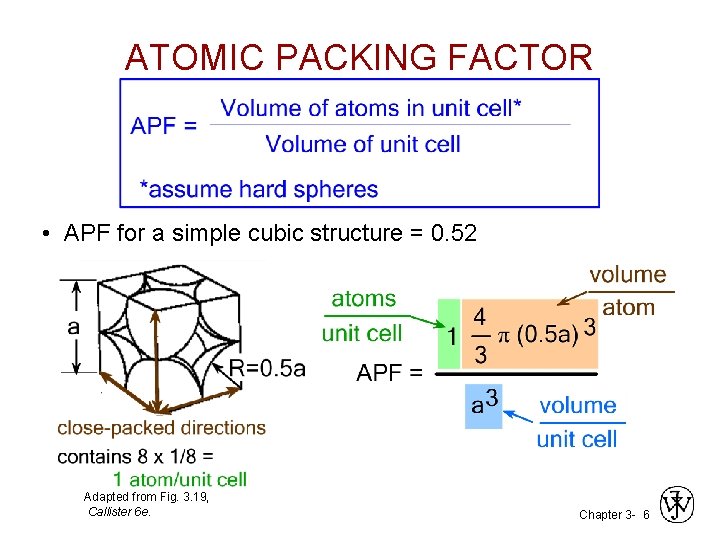
ATOMIC PACKING FACTOR • APF for a simple cubic structure = 0. 52 Adapted from Fig. 3. 19, Callister 6 e. Chapter 3 - 6

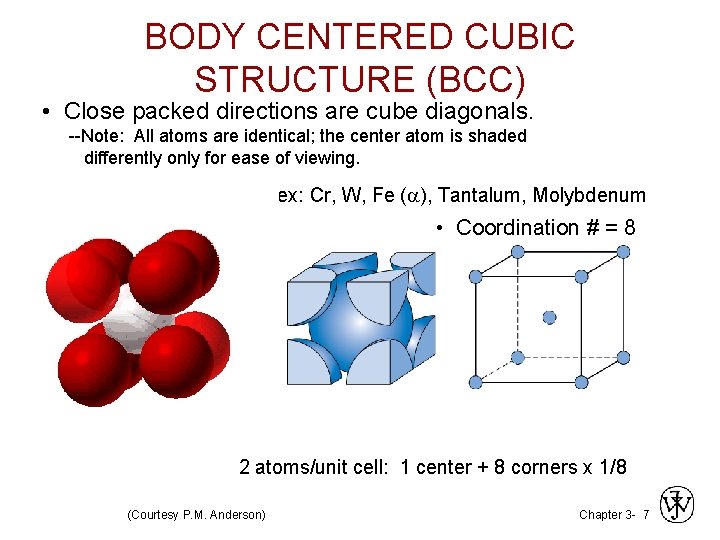
BODY CENTERED CUBIC STRUCTURE (BCC) • Close packed directions are cube diagonals. --Note: All atoms are identical; the center atom is shaded differently only for ease of viewing. ex: Cr, W, Fe ( ), Tantalum, Molybdenum • Coordination # = 8 2 atoms/unit cell: 1 center + 8 corners x 1/8 (Courtesy P. M. Anderson) Chapter 3 - 7

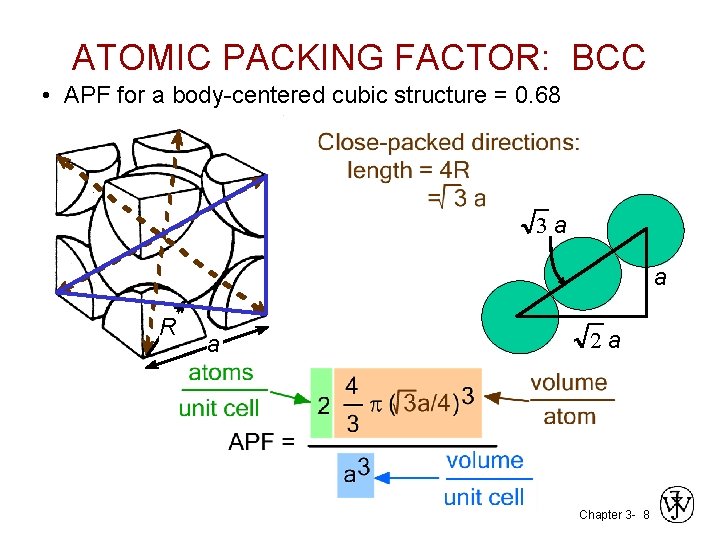
ATOMIC PACKING FACTOR: BCC • APF for a body-centered cubic structure = 0. 68 3 a a R a 2 a Chapter 3 - 8

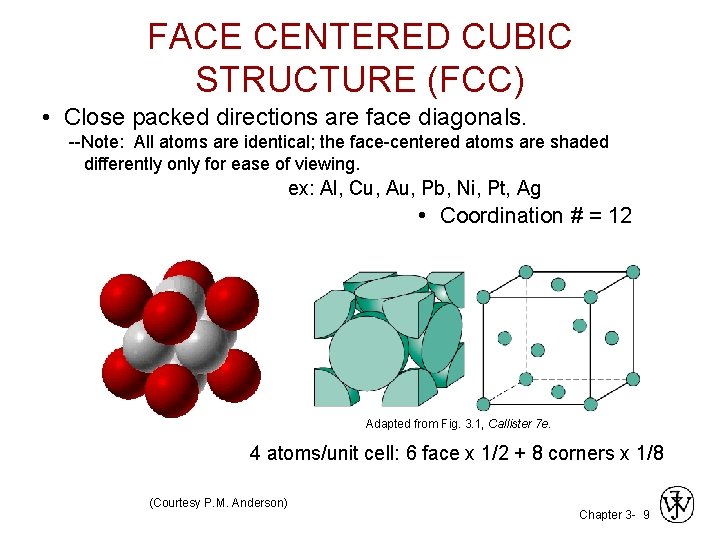
FACE CENTERED CUBIC STRUCTURE (FCC) • Close packed directions are face diagonals. --Note: All atoms are identical; the face-centered atoms are shaded differently only for ease of viewing. ex: Al, Cu, Au, Pb, Ni, Pt, Ag • Coordination # = 12 Adapted from Fig. 3. 1, Callister 7 e. 4 atoms/unit cell: 6 face x 1/2 + 8 corners x 1/8 (Courtesy P. M. Anderson) Chapter 3 - 9

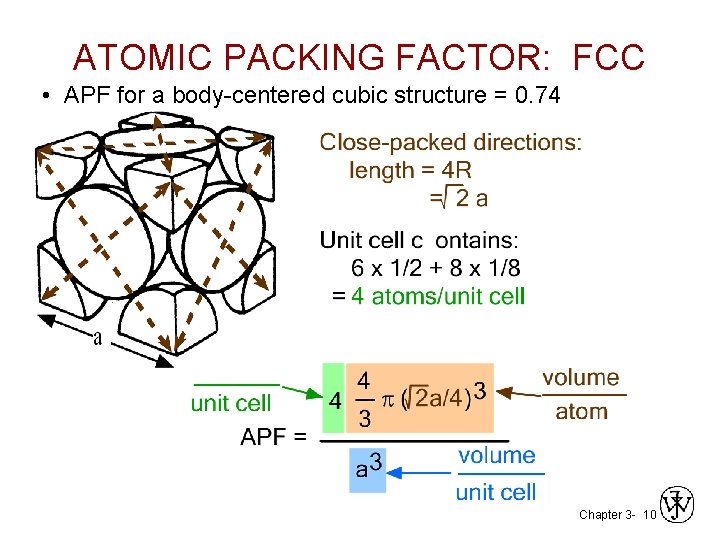
ATOMIC PACKING FACTOR: FCC • APF for a body-centered cubic structure = 0. 74 Chapter 3 - 10

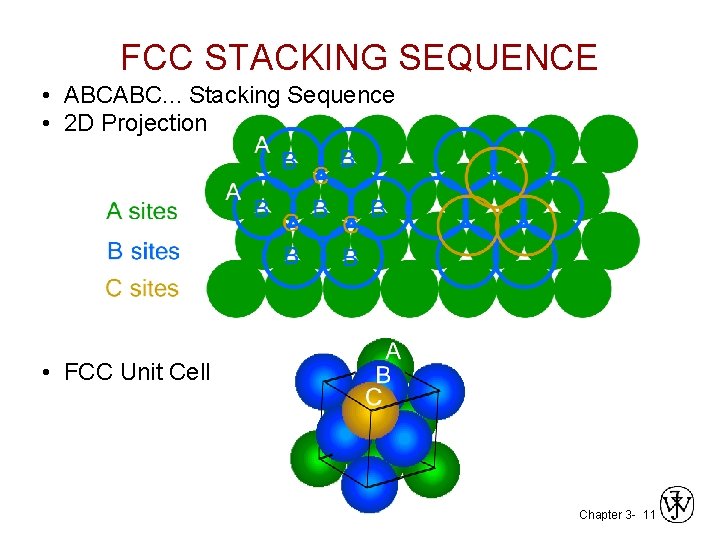
FCC STACKING SEQUENCE • ABCABC. . . Stacking Sequence • 2 D Projection • FCC Unit Cell Chapter 3 - 11

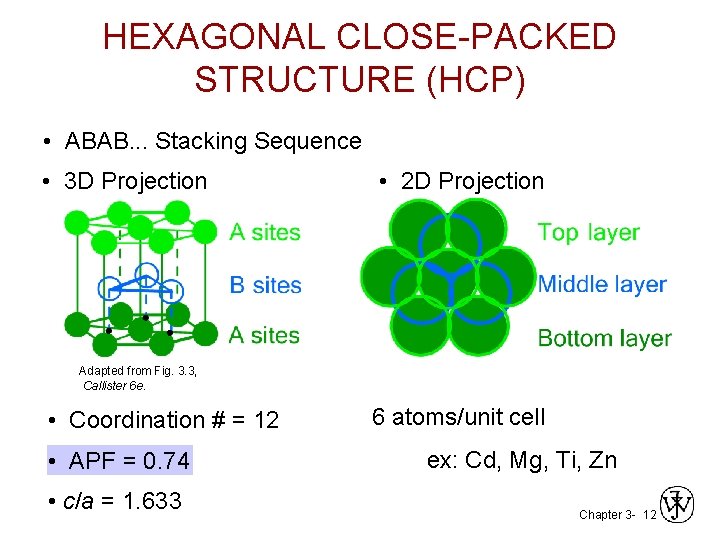
HEXAGONAL CLOSE-PACKED STRUCTURE (HCP) • ABAB. . . Stacking Sequence • 3 D Projection • 2 D Projection Adapted from Fig. 3. 3, Callister 6 e. • Coordination # = 12 • APF = 0. 74 • c/a = 1. 633 6 atoms/unit cell ex: Cd, Mg, Ti, Zn Chapter 3 - 12

STRUCTURE OF COMPOUNDS: Na. Cl • Compounds: Often have similar close-packed structures. • Structure of Na. Cl • Close-packed directions --along cube edges. (Courtesy P. M. Anderson) Chapter 3 - 13

Quotes from People in the know Arthur C. Clarke's Three Laws: 1)When a distinguished but elderly scientist states that something is possible, he is almost certainly right. When he states that something is impossible, he is very probably wrong. 2)The only way to discover the limits of the possible is to go beyond them into the impossible. 3)Any sufficiently advanced technology is indistinguishable from magic. (from Profiles of the Future, 1961) Chapter 3 -

THEORETICAL DENSITY, Example: Copper Data from Table inside front cover of Callister (see next slide): • crystal structure = FCC: 4 atoms/unit cell • atomic weight = 63. 55 g/mol (1 amu = 1 g/mol) -7 • atomic radius R = 0. 128 nm (1 nm = 10 cm) Chapter 3 - 14

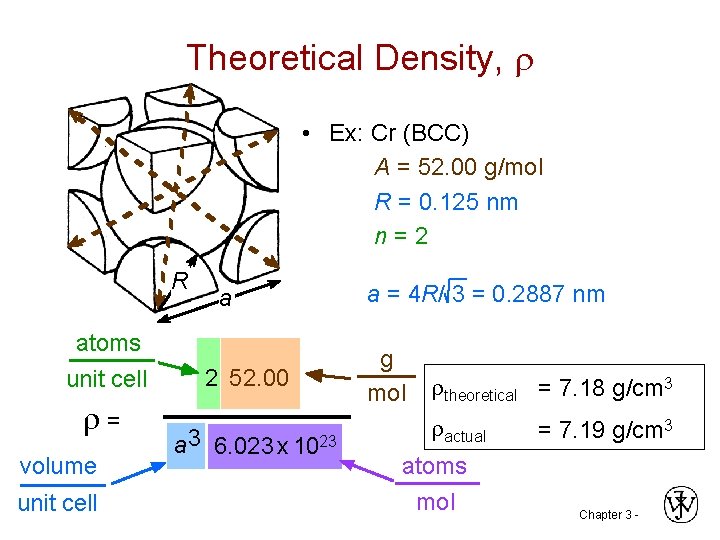
Theoretical Density, • Ex: Cr (BCC) A = 52. 00 g/mol R = 0. 125 nm n = 2 R atoms unit cell = volume unit cell a 2 52. 00 a 3 6. 023 x 1023 a = 4 R/ 3 = 0. 2887 nm g mol theoretical = 7. 18 g/cm 3 actual atoms mol = 7. 19 g/cm 3 Chapter 3 -

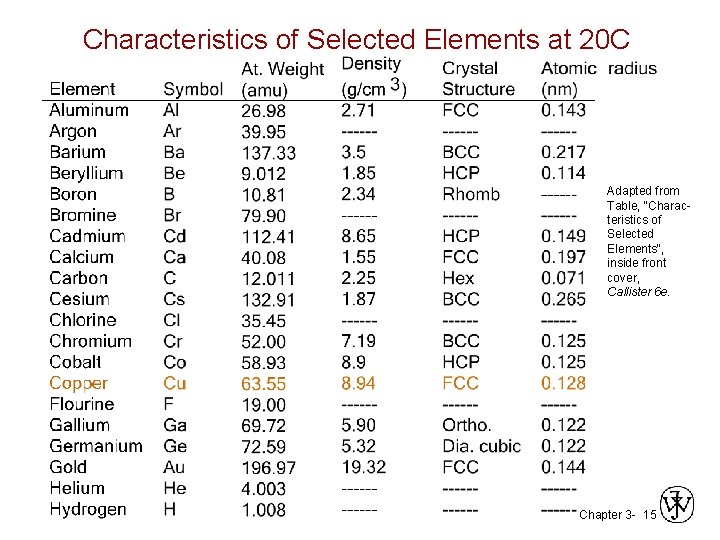
Characteristics of Selected Elements at 20 C Adapted from Table, "Characteristics of Selected Elements", inside front cover, Callister 6 e. Chapter 3 - 15

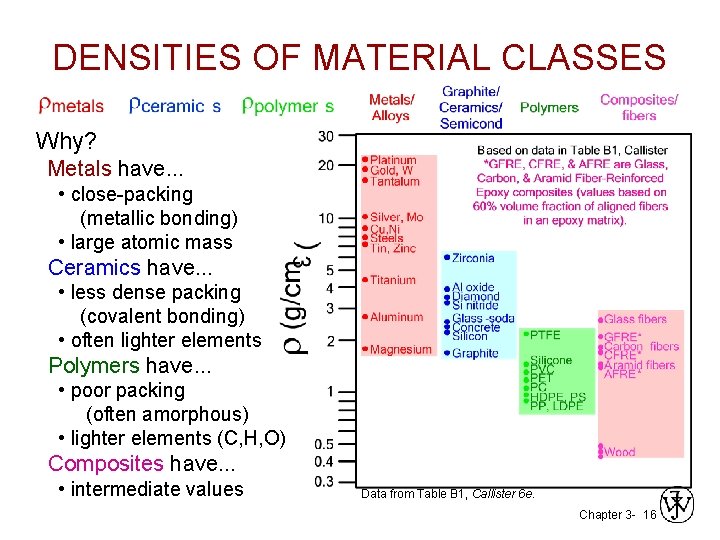
DENSITIES OF MATERIAL CLASSES Why? Metals have. . . • close-packing (metallic bonding) • large atomic mass Ceramics have. . . • less dense packing (covalent bonding) • often lighter elements Polymers have. . . • poor packing (often amorphous) • lighter elements (C, H, O) Composites have. . . • intermediate values Data from Table B 1, Callister 6 e. Chapter 3 - 16

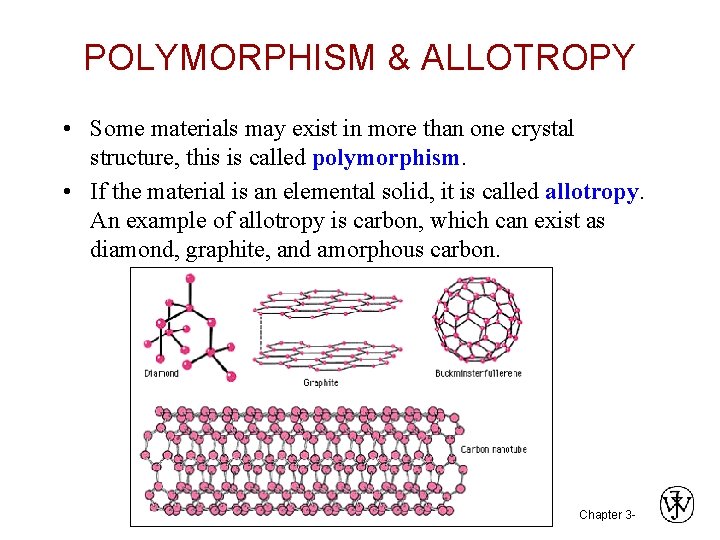
POLYMORPHISM & ALLOTROPY • Some materials may exist in more than one crystal structure, this is called polymorphism. • If the material is an elemental solid, it is called allotropy. An example of allotropy is carbon, which can exist as diamond, graphite, and amorphous carbon. Chapter 3 -

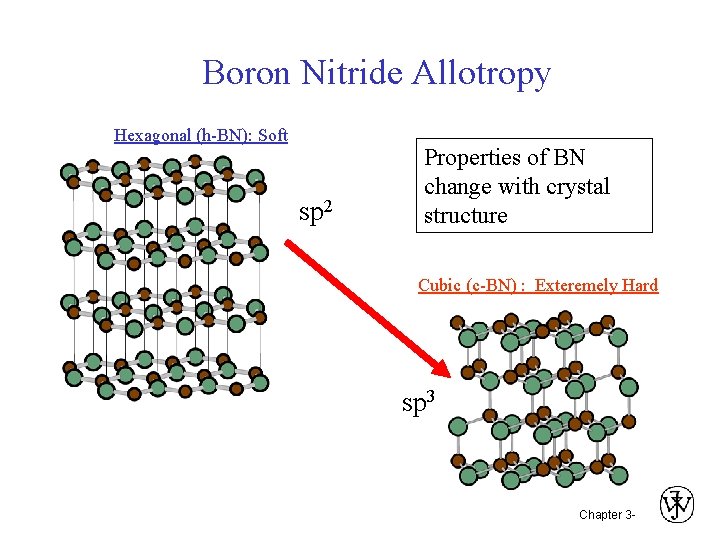
Boron Nitride Allotropy Hexagonal (h-BN): Soft sp 2 Properties of BN change with crystal structure Cubic (c-BN) : Exteremely Hard sp 3 Chapter 3 -

Fullerenes B 36 N 36 B 12 N 12 4. 3 Å B N C C 60 7. 2 Å 6. 8 Å Chapter 3 -

Crystallographic Points, Directions, and Planes • It is necessary to specify a particular point/location/atom/direction/plane in a unit cell • We need some labeling convention. Simplest way is to use a 3 -D system, where every location can be expressed using three numbers or indices. z – a, b, c and α, β, γ α β y γ x Chapter 3 -

Crystallographic Points, Directions, and Planes • Crystallographic direction is a vector [uvw] – Always passes thru origin 000 – Measured in terms of unit cell dimensions a, b, and c – Smallest integer values • Planes with Miller Indices (hkl) – If plane passes thru origin, translate – Length of each planar intercept in terms of the lattice parameters a, b, and c. – Reciprocals are taken – If needed multiply by a common factor for integer representation Chapter 3 -

Section 3. 8 Point Coordinates z Point coordinates for unit cell center are 111 c a/2, b/2, c/2 ½ ½ ½ 000 a y b Point coordinates for unit cell corner are 111 x z 2 c b y Translation: integer multiple of lattice constants identical position in another unit cell b Chapter 3 -

Crystallographic Directions Algorithm z y 1. Vector repositioned (if necessary) to pass through origin. 2. Read off projections in terms of unit cell dimensions a, b, and c 3. Adjust to smallest integer values 4. Enclose in square brackets, no commas [uvw] x ex: 1, 0, ½ => 2, 0, 1 => [ 201 ] -1, 1, 1 => [ 111 ] where overbar represents a negative index families of directions <uvw> Chapter 3 -

Linear Density • Linear Density of Atoms LD = [110] a Number of atoms Unit length of direction vector ex: linear density of Al in [110] direction a = 0. 405 nm # atoms LD = length 2 2 a = 3. 5 nm -1 Chapter 3 -

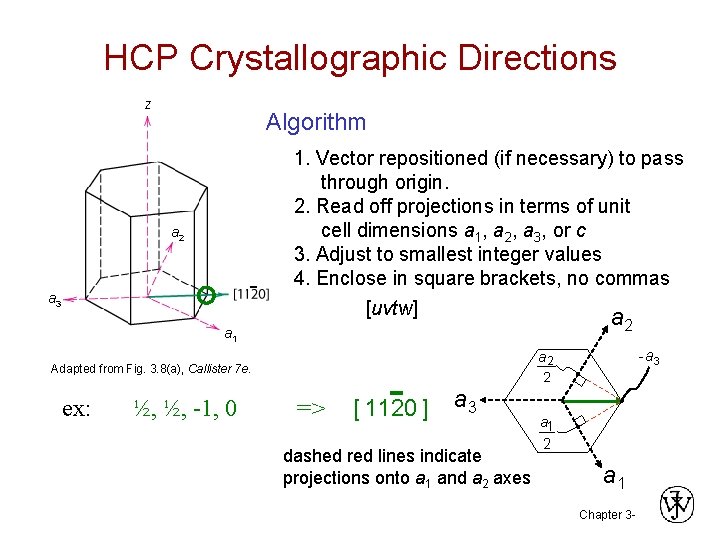
HCP Crystallographic Directions z Algorithm a 2 - a 3 a 1 1. Vector repositioned (if necessary) to pass through origin. 2. Read off projections in terms of unit cell dimensions a 1, a 2, a 3, or c 3. Adjust to smallest integer values 4. Enclose in square brackets, no commas [uvtw] a 2 -a 3 a 2 2 Adapted from Fig. 3. 8(a), Callister 7 e. ex: ½, ½, -1, 0 => [ 1120 ] a 3 dashed red lines indicate projections onto a 1 and a 2 axes a 1 2 a 1 Chapter 3 -

HCP Crystallographic Directions • Hexagonal Crystals – 4 parameter Miller-Bravais lattice coordinates are related to the direction indices (i. e. , u'v'w') as follows. z [ u 'v 'w ' ] ® [ uvtw ] a 2 - a 3 a 1 1 u = (2 u ' - v ') 3 1 v = (2 v ' - u ') 3 t = - ( u +v ) w = w' Fig. 3. 8(a), Callister 7 e. Chapter 3 -

Crystallographic Planes Adapted from Fig. 3. 9, Callister 7 e. Chapter 3 -

Crystallographic Planes • Miller Indices: Reciprocals of the (three) axial intercepts for a plane, cleared of fractions & common multiples. All parallel planes have same Miller indices. • Algorithm 1. Read off intercepts of plane with axes in terms of a, b, c 2. Take reciprocals of intercepts 3. Reduce to smallest integer values 4. Enclose in parentheses, no commas i. e. , (hkl) Chapter 3 -

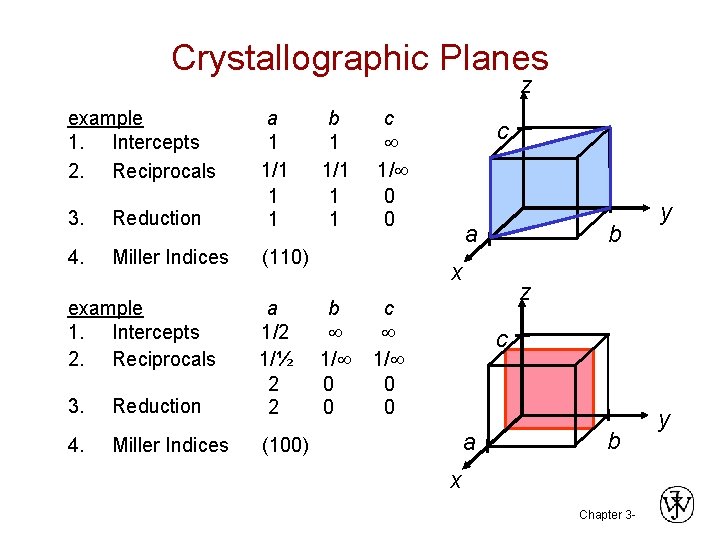
Crystallographic Planes z example 1. Intercepts 2. Reciprocals 3. Reduction a b c 1 1/1 1/ 1 1 0 4. Miller Indices (110) example 1. Intercepts 2. Reciprocals 3. Reduction c b a x a b c 1/2 1/½ 1/ 1/ 2 0 0 y z c a 4. Miller Indices (100) b x Chapter 3 - y

Crystallographic Planes z example 1. Intercepts 2. Reciprocals a b c c 1/2 1 3/4 1/½ 1/1 1/¾ 2 1 4/3 3. Reduction 6 3 4 a x 4. Miller Indices (634) b Family of Planes {hkl} Ex: {100} = (100), (010), (001), (100), (010), (001) Chapter 3 - y

Crystallographic Planes (HCP) • In hexagonal unit cells the same idea is used z example 1. Intercepts 2. Reciprocals 3. Reduction a 1 a 2 a 3 c 1 -1 1 1 1/ -1 1 1 0 -1 1 a 2 a 3 4. Miller-Bravais Indices (1011) a 1 Adapted from Fig. 3. 8(a), Callister 7 e. Chapter 3 -

Crystallographic Planes • • We want to examine the atomic packing of crystallographic planes Iron foil can be used as a catalyst. The atomic packing of the exposed planes is important. a) Draw (100) and (111) crystallographic planes for Fe. b) Calculate the planar density for each of these planes. Chapter 3 -

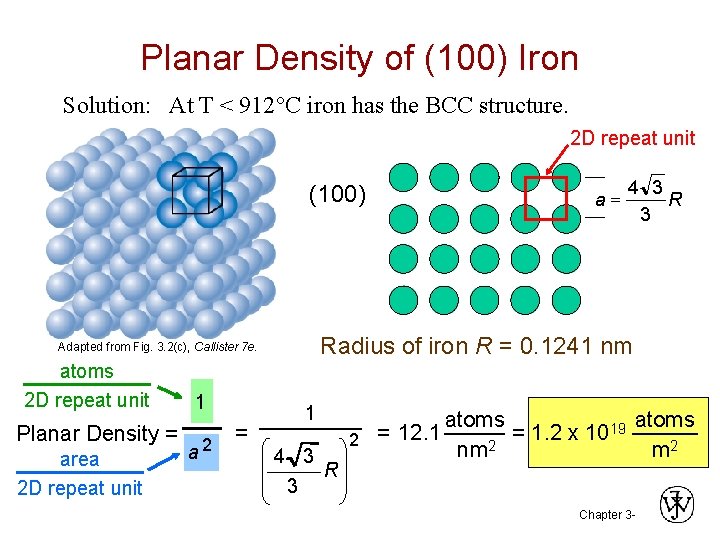
Planar Density of (100) Iron Solution: At T < 912 C iron has the BCC structure. 2 D repeat unit (100) 1 Planar Density = 2 a area 2 D repeat unit = 4 3 Radius of iron R = 0. 1241 nm Adapted from Fig. 3. 2(c), Callister 7 e. atoms 2 D repeat unit a= 1 4 3 R 3 atoms 19 = 1. 2 x 10 2 = 12. 1 2 nm m 2 Chapter 3 -

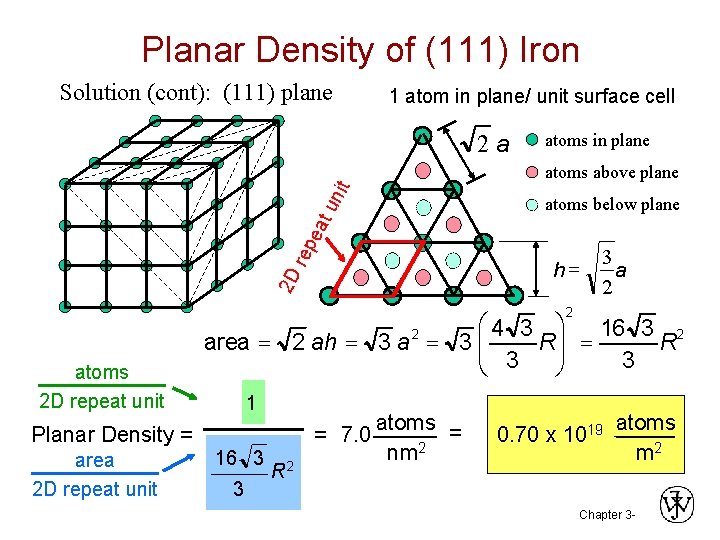
Planar Density of (111) Iron Solution (cont): (111) plane 1 atom in plane/ unit surface cell 2 a atoms in plane un it atoms above plane re pe at atoms below plane 2 D h= 3 a 2 2 atoms 2 D repeat unit Planar Density = area 2 D repeat unit æ 4 3 ö 16 3 2 2 area = 2 ah = 3 a = 3 çç R ÷÷ = R 3 è 3 ø 1 16 3 3 = 7. 0 R 2 atoms = nm 2 0. 70 x 1019 atoms m 2 Chapter 3 -

Single Crystals and Polycrystalline Materials • In a single crystal material the periodic and repeated arrangement of atoms is PERFECT This extends throughout the entirety of the specimen without interruption. • Polycrystalline material, on the other hand, is comprised of many small crystals or grains. The grains have different crystallographic orientation. There exist atomic mismatch within the regions where grains meet. These regions are called grain boundaries. Chapter 3 -

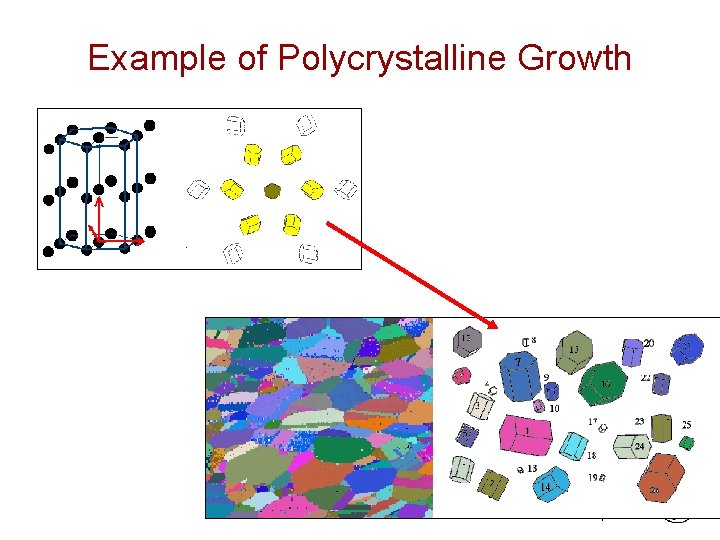
Example of Polycrystalline Growth Chapter 3 -

CRYSTALS AS BUILDING BLOCKS • Some engineering applications require single crystals: --diamond single crystals for abrasives --turbine blades (Courtesy Martin Deakins, GE Superabrasives, Worthington, OH. Used with permission. ) Fig. 8. 30(c), Callister 6 e. (Fig. 8. 30(c) courtesy of Pratt and Whitney). • Crystal properties reveal features of atomic structure. --Ex: Certain crystal planes in quartz fracture more easily than others. (Courtesy P. M. Anderson) Chapter 3 - 17

POLYCRYSTALS • Most engineering materials are polycrystals. 1 mm Adapted from Fig. K, color inset pages of Callister 6 e. (Fig. K is courtesy of Paul E. Danielson, Teledyne Wah Chang Albany) • Nb-Hf-W plate with an electron beam weld. • Each "grain" is a single crystal. • If crystals are randomly oriented, overall component properties are not directional. • Crystal sizes typ. range from 1 nm to 2 cm (i. e. , from a few to millions of atomic layers). Chapter 3 - 18

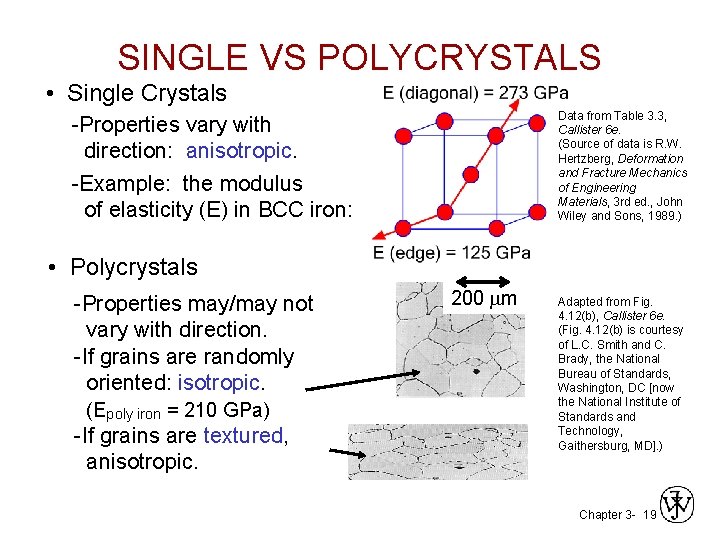
SINGLE VS POLYCRYSTALS • Single Crystals Data from Table 3. 3, Callister 6 e. (Source of data is R. W. Hertzberg, Deformation and Fracture Mechanics of Engineering Materials, 3 rd ed. , John Wiley and Sons, 1989. ) -Properties vary with direction: anisotropic. -Example: the modulus of elasticity (E) in BCC iron: • Polycrystals -Properties may/may not vary with direction. -If grains are randomly oriented: isotropic. (Epoly iron = 210 GPa) -If grains are textured, anisotropic. 200 mm Adapted from Fig. 4. 12(b), Callister 6 e. (Fig. 4. 12(b) is courtesy of L. C. Smith and C. Brady, the National Bureau of Standards, Washington, DC [now the National Institute of Standards and Technology, Gaithersburg, MD]. ) Chapter 3 - 19

Anisotropy and Texture • Different directions in a crystal have a different APF. • For instance, atoms along the edge of FCC unit cell are more separated than along the face diagonal. This causes anisotropy in the properties of crystals. • For example, the deformation amount depends on the direction in which a stress is applied, other properties are thermal conductivity, optical properties, magnetic properties, hardness, etc. • In some polycrystalline materials, grain orientations are random, hence bulk material properties are isotropic, i. e. equivalent in each direction • Some polycrystalline materials have grains with preferred orientations (texture), so properties are dominated by those relevant to the texture orientation and the material exhibits anisotropic properties. Chapter 3 -

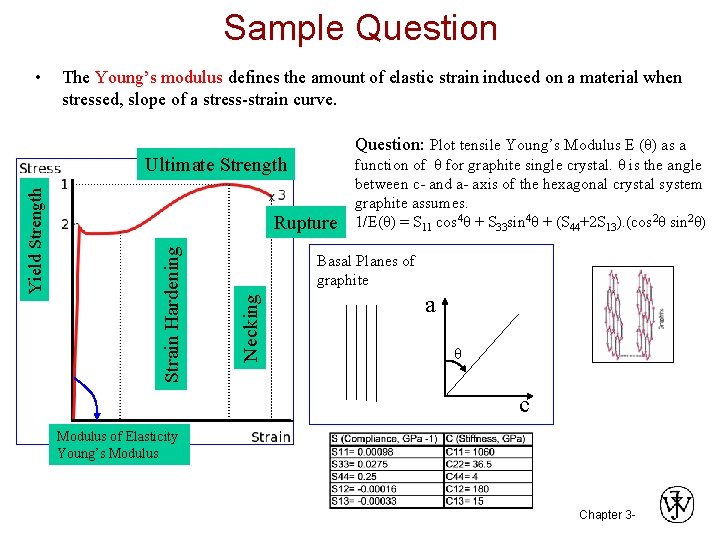
Sample Question • The Young’s modulus defines the amount of elastic strain induced on a material when stressed, slope of a stress-strain curve. Question: Plot tensile Young’s Modulus E (θ) as a Rupture function of θ for graphite single crystal. θ is the angle between c- and a- axis of the hexagonal crystal system graphite assumes. 1/E(θ) = S 11 cos 4θ + S 33 sin 4θ + (S 44+2 S 13). (cos 2θ sin 2θ) Basal Planes of graphite Necking Strain Hardening Yield Strength Ultimate Strength a θ c Modulus of Elasticity Young’s Modulus Chapter 3 -

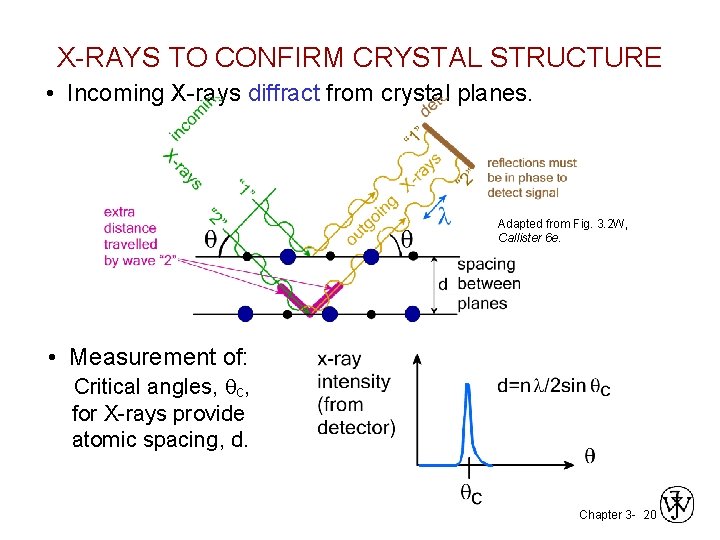
X-RAYS TO CONFIRM CRYSTAL STRUCTURE • Incoming X-rays diffract from crystal planes. Adapted from Fig. 3. 2 W, Callister 6 e. • Measurement of: Critical angles, qc, for X-rays provide atomic spacing, d. Chapter 3 - 20

SCANNING TUNNELING MICROSCOPY • Atoms can be arranged and imaged Photos produced from the work of C. P. Lutz, Zeppenfeld, and D. M. Eigler. Reprinted with permission from International Business Machines Corporation, copyright 1995. Carbon monoxide molecules arranged on a platinum (111) surface. Iron atoms arranged on a copper (111) surface. These Kanji characters represent the word “atom”. Chapter 3 - 21

DEMO: HEATING AND COOLING OF AN IRON WIRE • Demonstrates "polymorphism" The same atoms can have more than one crystal structure. Chapter 3 - 22

SUMMARY (I) • Atoms may assemble into crystalline or amorphous structures. • We can predict the density of a material, provided we know the atomic weight, atomic radius, and crystal geometry (e. g. , FCC, BCC, HCP). • Material properties generally vary with single crystal orientation (i. e. , they are anisotropic), but properties are generally non-directional (i. e. , they are isotropic) in polycrystals with randomly oriented grains. Chapter 3 - 23

Summary (II) • • • • • Allotropy Amorphous Anisotropy Atomic packing factor (APF) Body-centered cubic (BCC) Coordination number Crystal structure Crystalline Face-centered cubic (FCC) Grain boundary Hexagonal close-packed (HCP) Isotropic Lattice parameter Non-crystalline Polymorphism Single crystal Unit cell Chapter 3 -

Midterm Dates And Places • Midterm 1: Place and Time • Midterm 2: Place and Time. • Final: To be decided by the Faculty of Engineering. Chapter 3 -

ANNOUNCEMENTS Reading: Read and work on the examples of Chapter 3 multiple times. Visit the Virtual Materials Science Engineering Website link listed in your book and go thru the different Crystal Structures ! Core Problems: 3. 14, 3. 15, 3. 20, 3. 31, 3. 39, 3. 40, 3. 54 Bonus Problems: 3. 26 (? ), 3. 32, 3. 41, 3. 42, 3. 51, 3. 53 Due Date: 6 March 2008 Chapter 3 - 0