Why do we always speak of beta decay

Why do we always speak of beta decay as a process “governed by the WEAK FORCE”? What do DECAYS have to do with FORCE? Where’s the FORCE FIELD? What IS the FORCE FIELD? What VECTOR PARTICLE is exchanged? e- What’s been “seen” n semi-leptonic decays + + _ e p leptonic decay We’ve identified complicated 4 -branch vertices, but only for the mediating BOSONS… Not the FERMIONS! e _ e

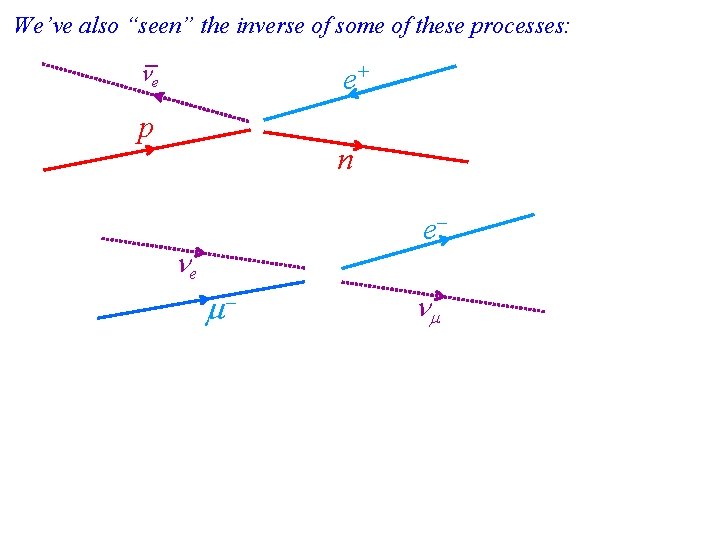
We’ve also “seen” the inverse of some of these processes: _ e e+ p n e e

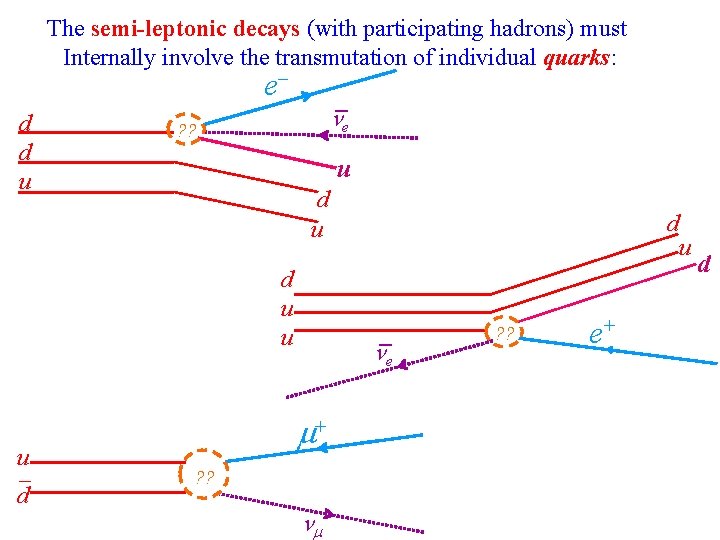
The semi-leptonic decays (with participating hadrons) must Internally involve the transmutation of individual quarks: e d d u _ e ? ? u d u u u_ d d u _ e + ? ? e+ d

Protons, quarks, pions and muons are all electrically charged so do participate in: e p Can we use QED as a prototype by comparing or to lepton baryon e e ? ? ? p Charge-carrying currents imply a charged vector boson exchange! n (we’ve already seen gluons carry color)

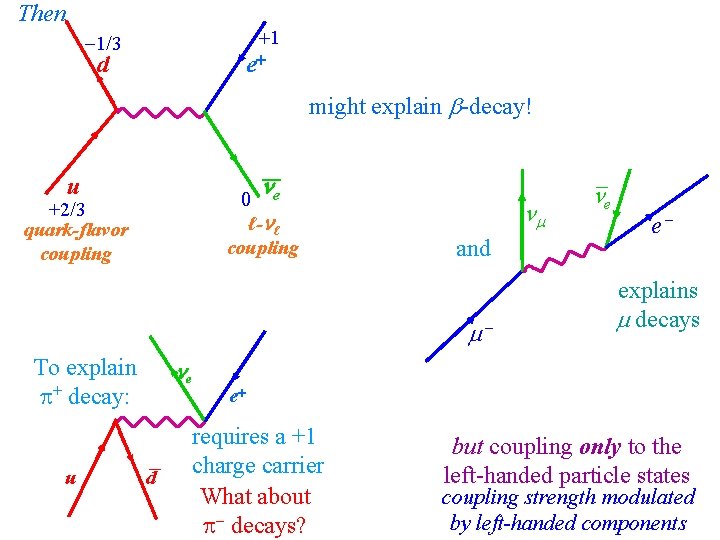
Then +1 1/3 e+ d might explain -decay! _ e u 0 ℓ- ℓ coupling +2/3 quark-flavor coupling and To explain + decay: u e _ d e e explains decays e+ requires a +1 charge carrier What about decays? but coupling only to the left-handed particle states coupling strength modulated by left-handed components

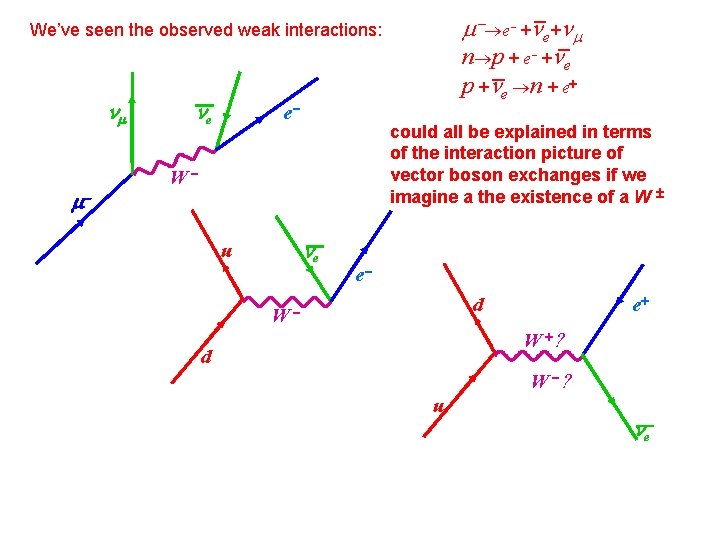
e + e+ n p + e n + e+ We’ve seen the observed weak interactions: m m- e e- could all be explained in terms of the interaction picture of vector boson exchanges if we imagine a the existence of a W W- e u W ee+ d - W +? d W -? u e

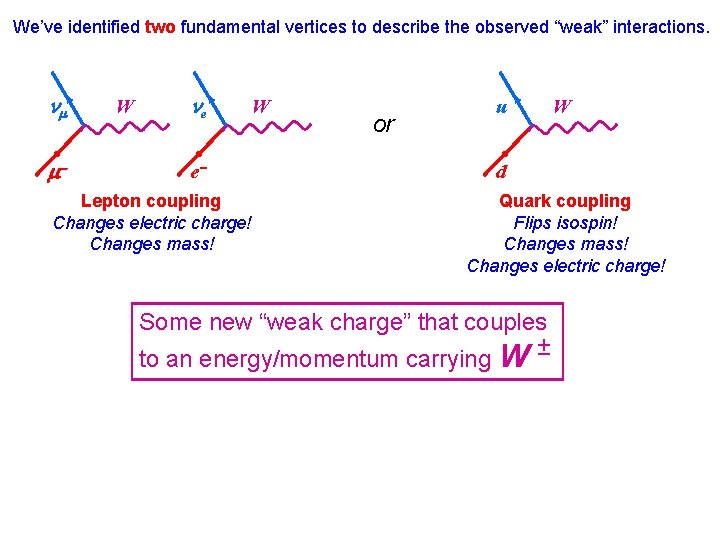
We’ve identified two fundamental vertices to describe the observed “weak” interactions. m m- W e e- Lepton coupling Changes electric charge! Changes mass! W or u W d Quark coupling Flips isospin! Changes mass! Changes electric charge! Some new “weak charge” that couples to an energy/momentum carrying W ±

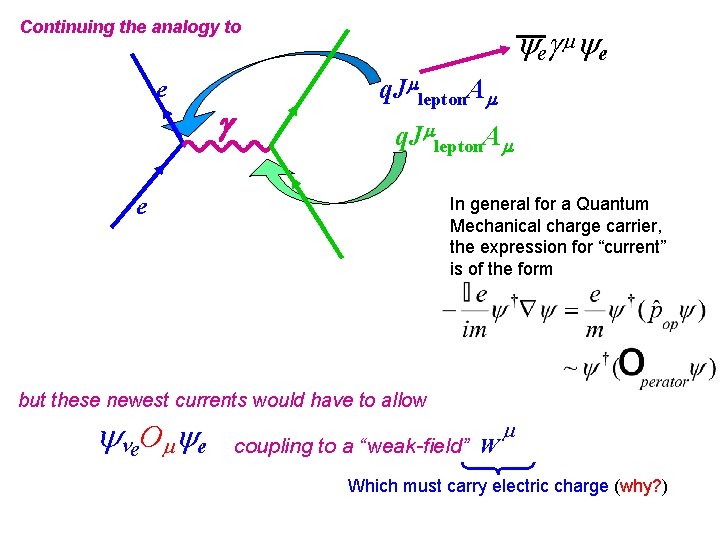
Continuing the analogy to e g e e q. Jmlepton. Am e In general for a Quantum Mechanical charge carrier, the expression for “current” is of the form but these newest currents would have to allow e O e coupling to a “weak-field” W Which must carry electric charge (why? ) but not couple to it (why? )

If this interaction reflects a symmetry, how many weak fields must there be? U(1) one field (the photon) SU(2) YANG MILLS: 3 fields SU(3) COLOR: 8 fields (gluons) U(1) is clearly inadequate U(2) would mean 3 weak fields we know we need W+, W Could there be a neutral W 0 ? But YANG-MILLS assumes we have “ISO”DOUBLET states!

We’ve discovered we do have: Left-handed weak iso-doublets (in a new weak “iso”-space) u d L e e- L Right-handed weak iso-singlets u. R d. R e. R NOT part of a doublet… NOT linked by the weak force to neutrinos NOTE: there is NO ( e )R

Left-handed weak iso-doublets (in a new weak “iso”-space) u d L +½ -½ e e- Right-handed weak iso-singlets u. R d. R e. R 0 0 0 With ISO-SPIN we identified a complimentary “hypercharge” representing another quantum value that could be simultaneously diagonalized with ISO-SPIN operators. We generalize that concept into a NEW HYPERCHARGE in this “weak” space.

YL = 2 Q – 2 I 3 weak Left-handed I 3 weak u. L d. L +½ -½ YL = 2(2/3) – 2(1/2) = 1/3 YL = 2(-1/3) – 2(-1/2) = 1/3 ( e )L e -L +½ -½ YL = 2(0) – 2(+1/2) YL = 2(-1) – 2(-1/2) Right-handed u. R d. R e. R 0 0 0 YR = 2(Q) – 2(0) = 2 Q = -1

Not all weak participants have ELECTRIC CHARGE • Its NOT electric charge providing the coupling All weak participants (by definition) carry weak iso-spin u d L e e- L +½ -½ u W d e W But interactions are only well-defined by theory if the fermion legs to a vertex have equal coupling strengths e- u d L e e- L +½ -½ YL = 1/3 +½ -½ YL = -1 YL = 2 Q – 2 I 3 weak

With DOUBLET STATES and an associated “charge” defined we can attempt a Yang-Mills gauge-field model to explain the weak force but with some warnings. . .

The Yang-Mills theory requires introducing a 3 rd field: ee- W 0 Could this be the photon? How do we distinguish this process from exchange? Maybe the noted U(1) symmetry is part of a much larger symmetry: U(1) SU(2) ? U(1) ×SU(2) UEM(1) UY(1) ×SUL(2)

Straight from U(1) and the SU(2) Yang-Mills extension, consider: charge-like coupling to a photon-like field some new Yang. Mills coupling Ti= i/2 = 0 This looks like it could be Y g 1 with =q and for left-handed doublets for right-handed singlets U(1) B A 2 This all means we now work from a BIG comprehensive Lagrangian summed over all possible fermions f to include terms for u, d, c, s, t, b, e, , , e, ,

which contains, for example: plus similar terms for , , c, s, , , t, b,