Why are planes in a lattice important A

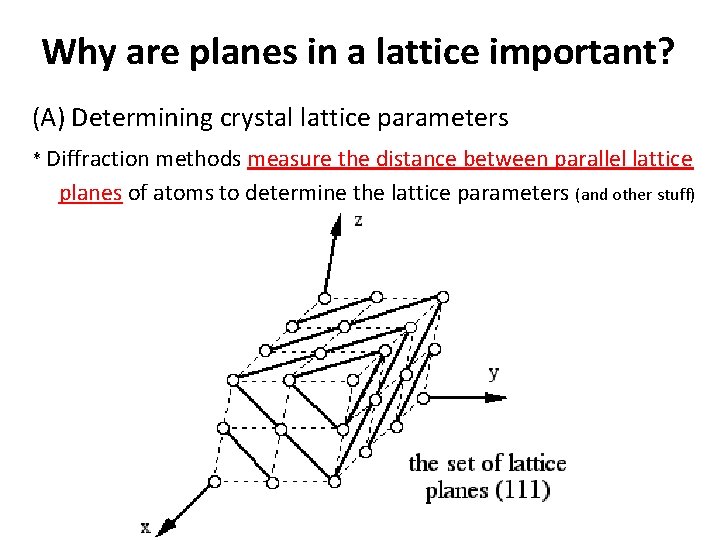
Why are planes in a lattice important? (A) Determining crystal lattice parameters * Diffraction methods measure the distance between parallel lattice planes of atoms to determine the lattice parameters (and other stuff)

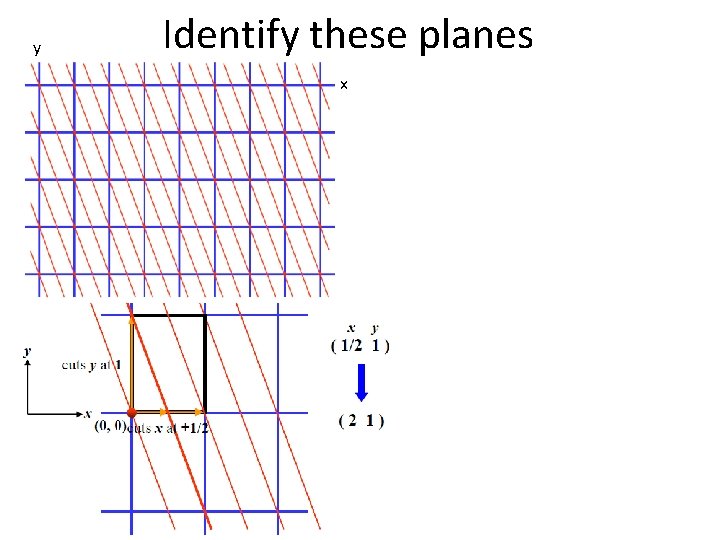
y Identify these planes x

y Identify these planes x

y Identify these planes x

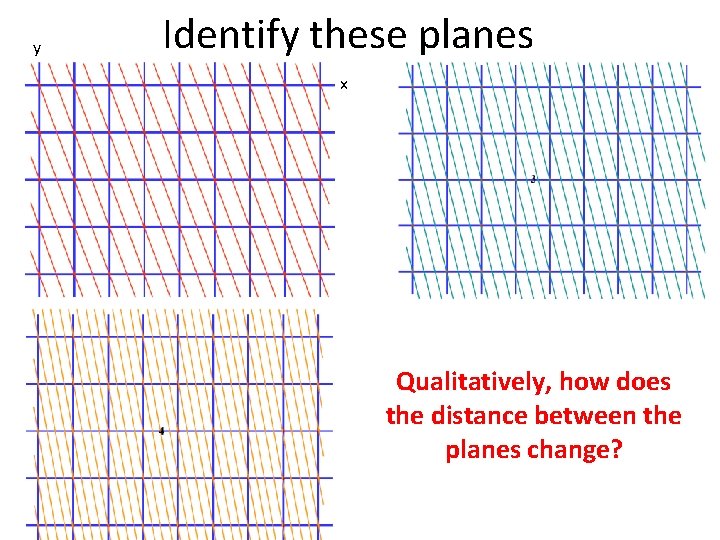
y Identify these planes x Qualitatively, how does the distance between the planes change?

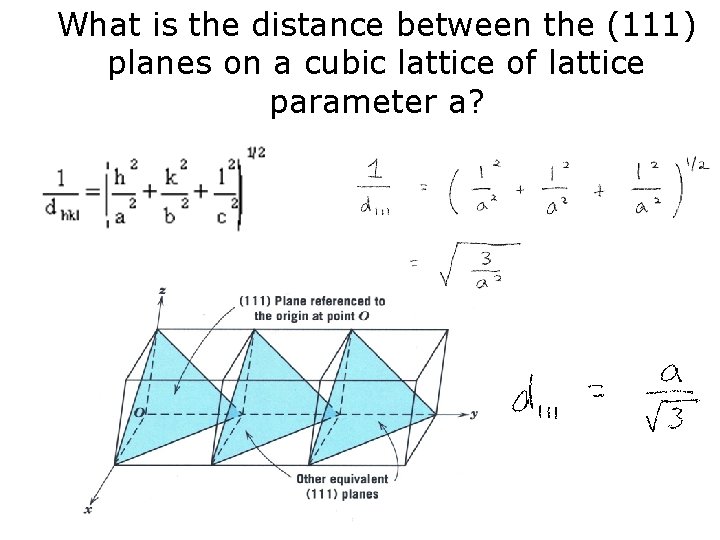
If you have orthorhombic tetragonal or cubic lattice, use this formula for distance between planes

If you have orthorhombic tetragonal or cubic lattice, use this formula for distance between planes

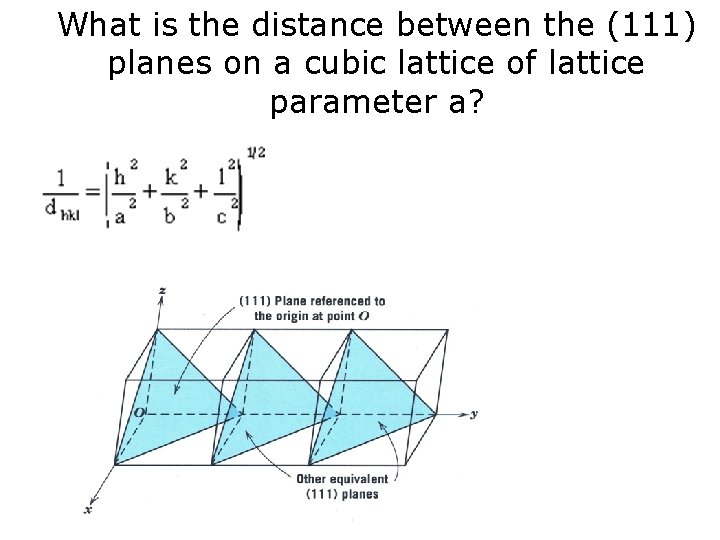
What is the distance between the (111) planes on a cubic lattice of lattice parameter a?

What is the distance between the (111) planes on a cubic lattice of lattice parameter a?

What is the distance between the (111) planes on a cubic lattice of lattice parameter a? Find the distance between (1 2 3) in a cubic lattice?

What is the distance between the (111) planes on a cubic lattice of lattice parameter a? Find d 111 in a tetragonal lattice where c = 2 a = 2 b?

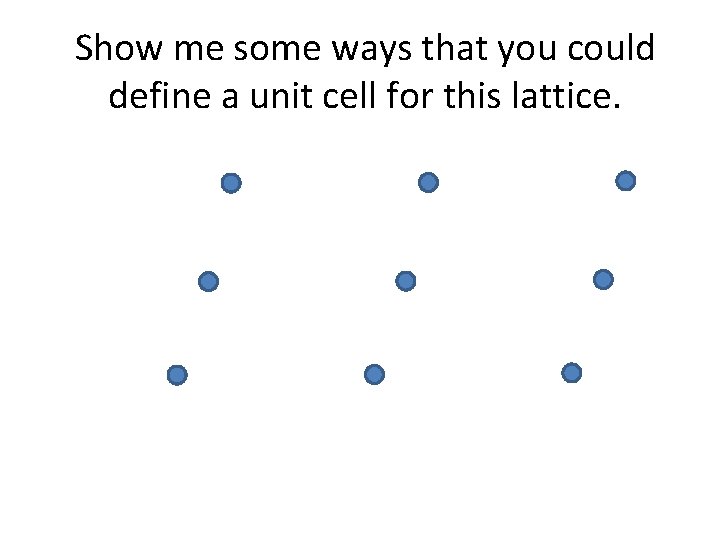
Show me some ways that you could define a unit cell for this lattice.

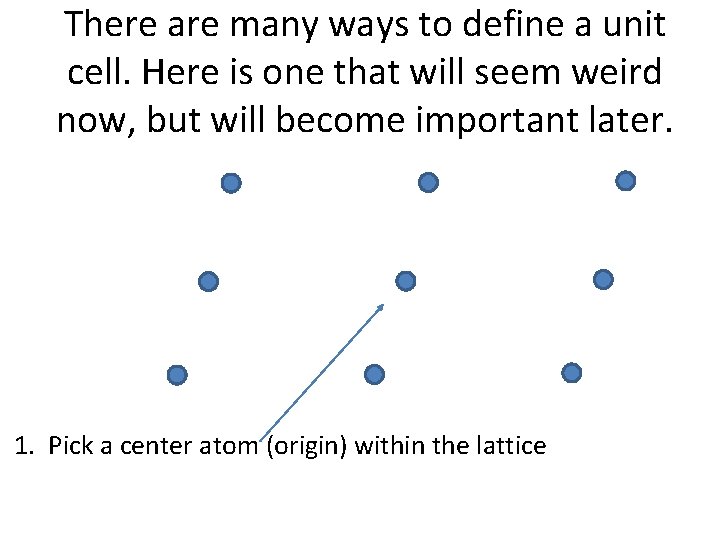
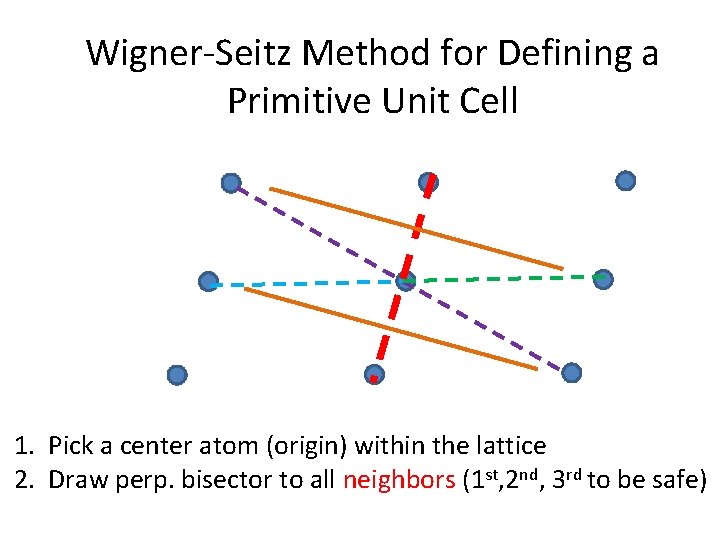
There are many ways to define a unit cell. Here is one that will seem weird now, but will become important later. 1. Pick a center atom (origin) within the lattice

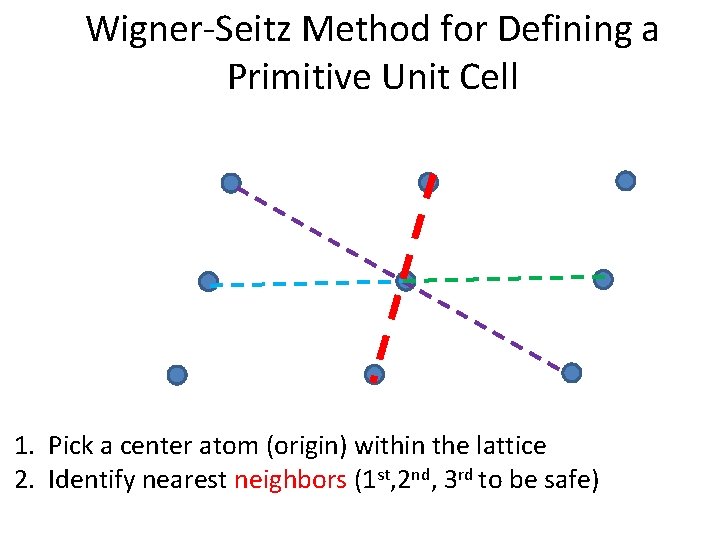
Wigner-Seitz Method for Defining a Primitive Unit Cell 1. Pick a center atom (origin) within the lattice 2. Identify nearest neighbors (1 st, 2 nd, 3 rd to be safe)

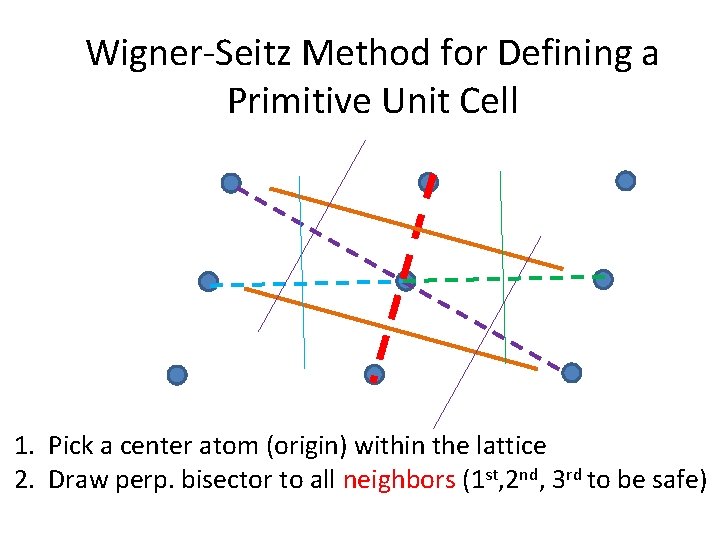
Wigner-Seitz Method for Defining a Primitive Unit Cell 1. Pick a center atom (origin) within the lattice 2. Draw perp. bisector to all neighbors (1 st, 2 nd, 3 rd to be safe)

Wigner-Seitz Method for Defining a Primitive Unit Cell 1. Pick a center atom (origin) within the lattice 2. Draw perp. bisector to all neighbors (1 st, 2 nd, 3 rd to be safe)

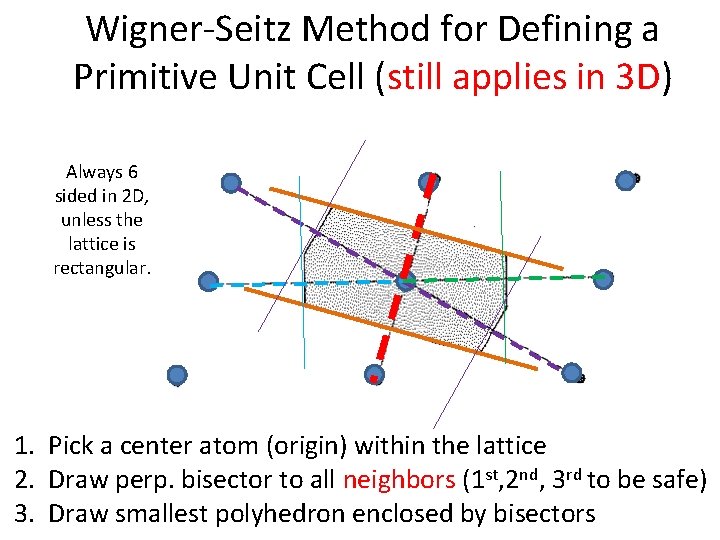
Wigner-Seitz Method for Defining a Primitive Unit Cell (still applies in 3 D) Always 6 sided in 2 D, unless the lattice is rectangular. 1. Pick a center atom (origin) within the lattice 2. Draw perp. bisector to all neighbors (1 st, 2 nd, 3 rd to be safe) 3. Draw smallest polyhedron enclosed by bisectors

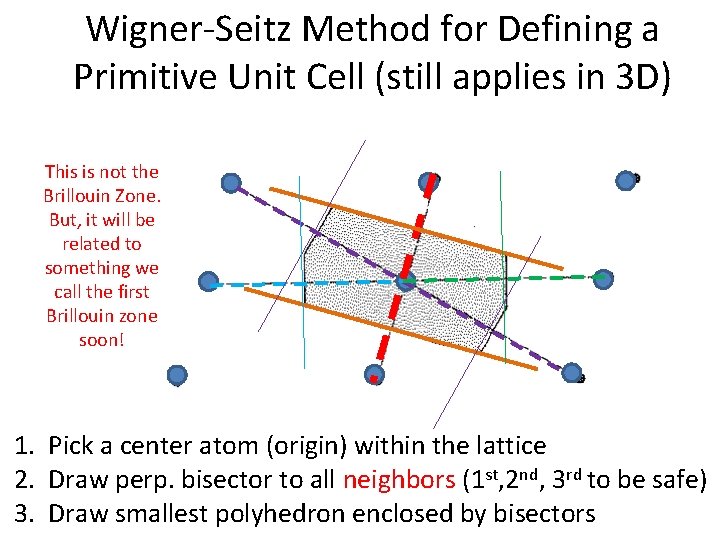
Wigner-Seitz Method for Defining a Primitive Unit Cell (still applies in 3 D) This is not the Brillouin Zone. But, it will be related to something we call the first Brillouin zone soon! 1. Pick a center atom (origin) within the lattice 2. Draw perp. bisector to all neighbors (1 st, 2 nd, 3 rd to be safe) 3. Draw smallest polyhedron enclosed by bisectors

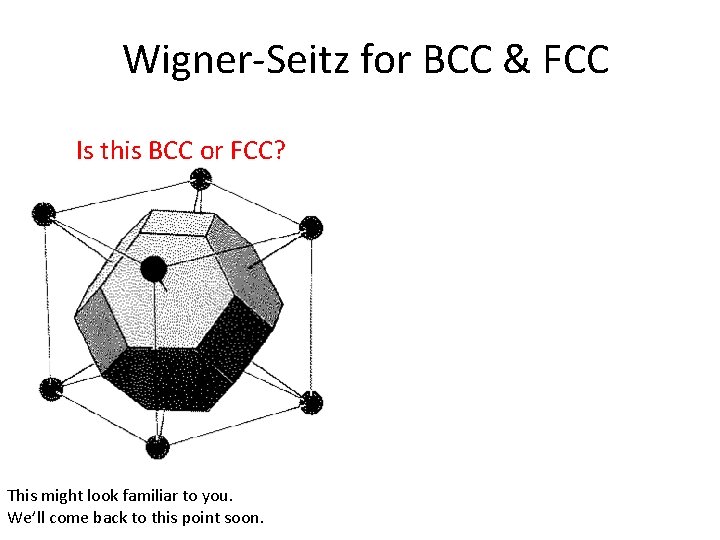
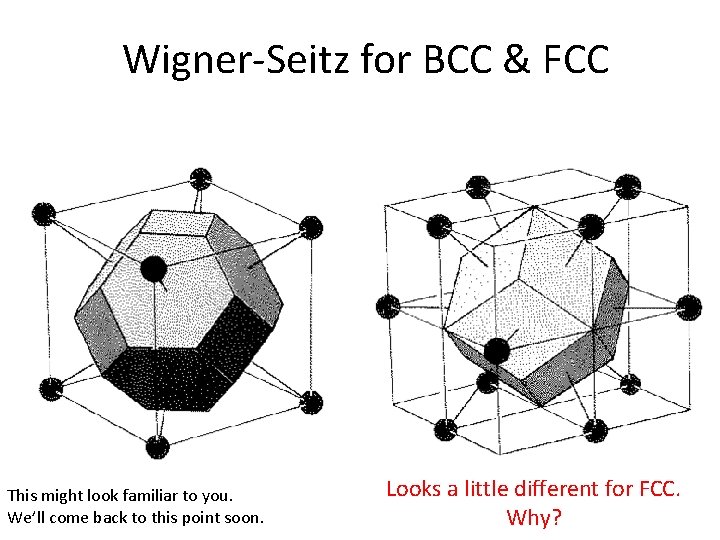
Wigner-Seitz for BCC & FCC Is this BCC or FCC? This might look familiar to you. We’ll come back to this point soon.

Wigner-Seitz for BCC & FCC This might look familiar to you. We’ll come back to this point soon. Looks a little different for FCC. Why?

Non-closed packed structures Ask any crystal structure questions today! For more information: https: //en. wikibooks. org/wiki/Introduction_to_Inorganic _Chemistry/Ionic_and_Covalent_Solids_-_Structures Next time: Diffraction

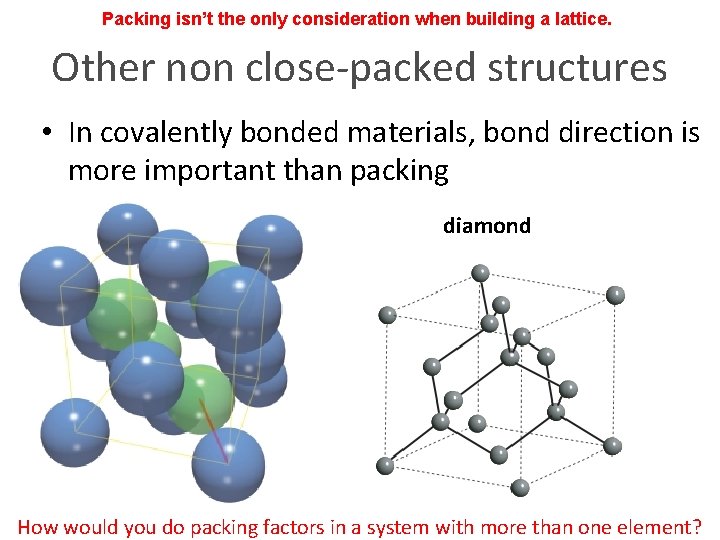
Packing isn’t the only consideration when building a lattice. Other non close-packed structures • In covalently bonded materials, bond direction is more important than packing graphite diamond How would you do packing factors in a system with more than one element?

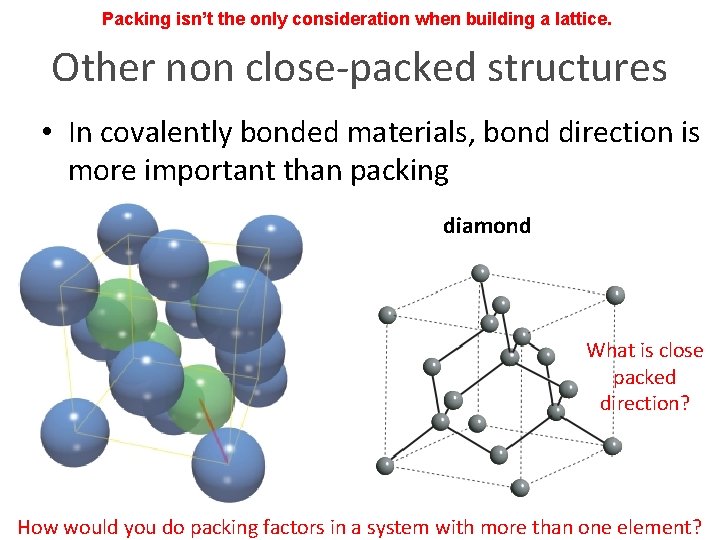
Packing isn’t the only consideration when building a lattice. Other non close-packed structures • In covalently bonded materials, bond direction is more important than packing graphite diamond What is close packed direction? How would you do packing factors in a system with more than one element?

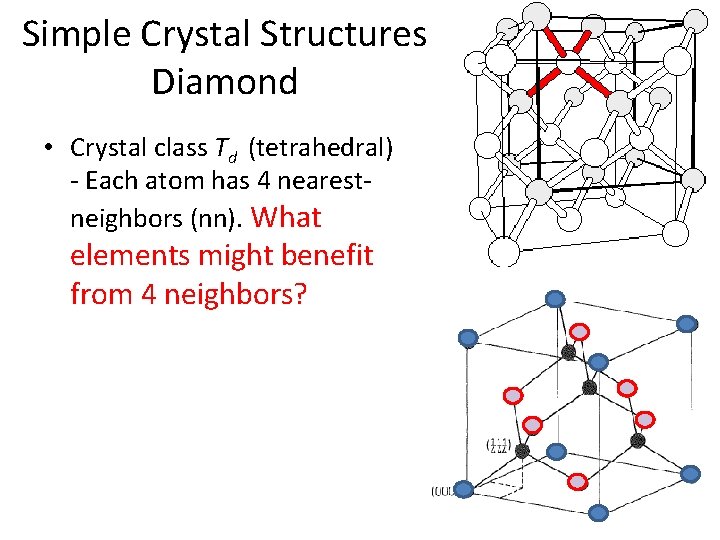
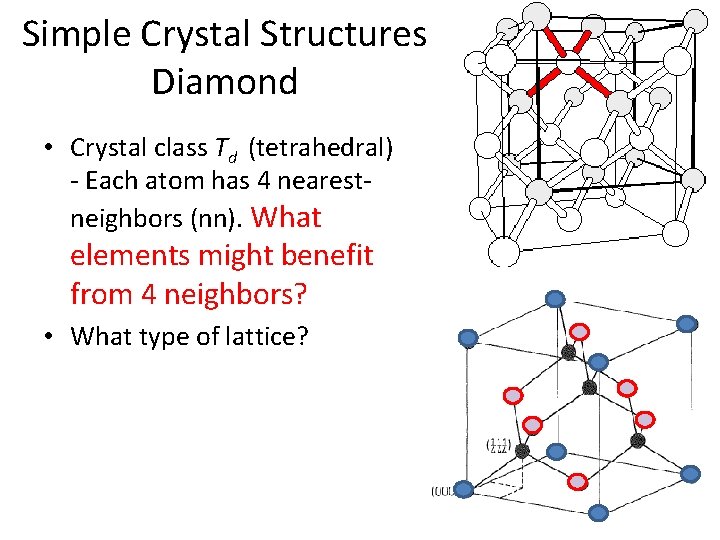
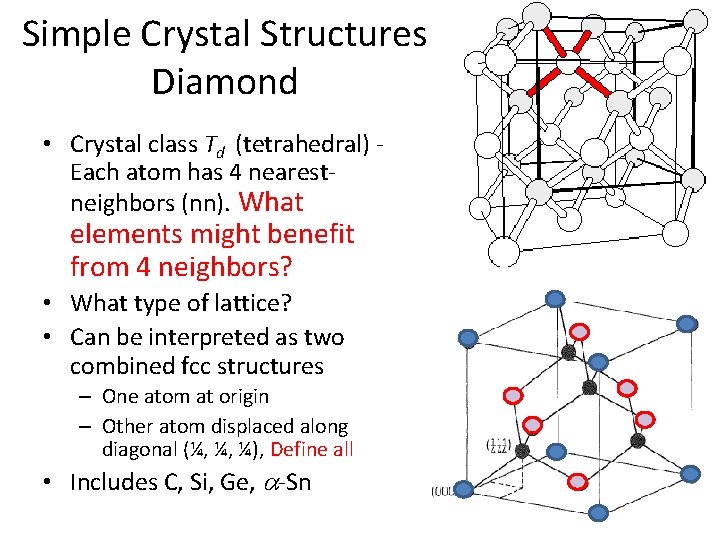
Simple Crystal Structures Diamond • Crystal class Td (tetrahedral) - Each atom has 4 nearestneighbors (nn). What elements might benefit from 4 neighbors?

Simple Crystal Structures Diamond • Crystal class Td (tetrahedral) - Each atom has 4 nearestneighbors (nn). What elements might benefit from 4 neighbors? • What type of lattice?

Simple Crystal Structures Diamond • Crystal class Td (tetrahedral) Each atom has 4 nearestneighbors (nn). What elements might benefit from 4 neighbors? • What type of lattice? • Can be interpreted as two combined fcc structures – One atom at origin – Other atom displaced along diagonal (¼, ¼, ¼), Define all • Includes C, Si, Ge, a-Sn

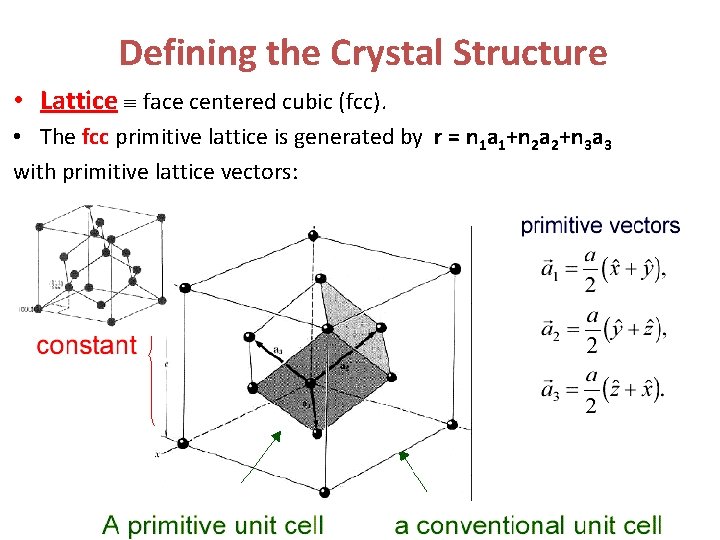
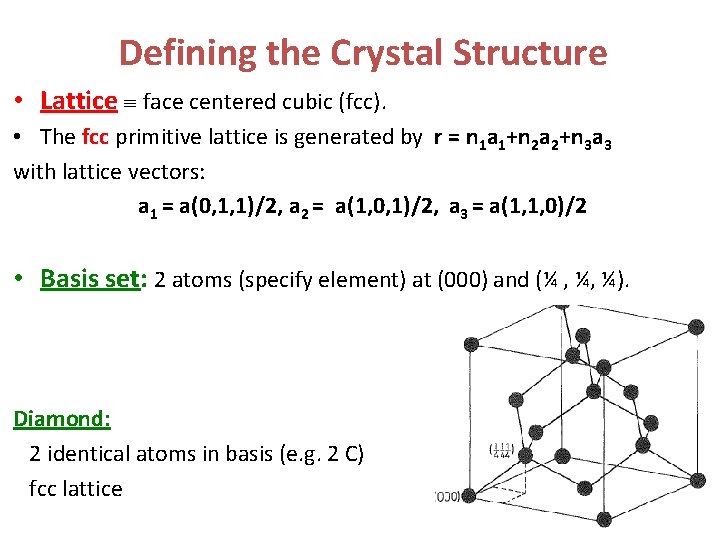
Defining the Crystal Structure • Lattice face centered cubic (fcc). • The fcc primitive lattice is generated by r = n 1 a 1+n 2 a 2+n 3 a 3 with primitive lattice vectors:

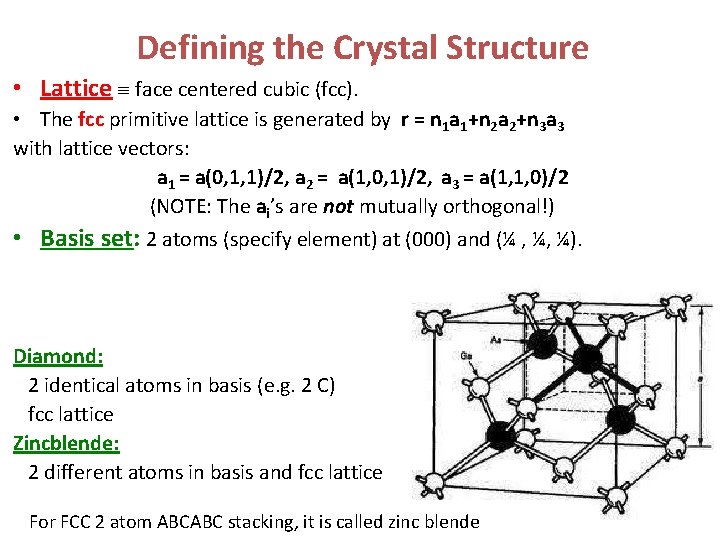
Defining the Crystal Structure • Lattice face centered cubic (fcc). • The fcc primitive lattice is generated by r = n 1 a 1+n 2 a 2+n 3 a 3 with lattice vectors: a 1 = a(0, 1, 1)/2, a 2 = a(1, 0, 1)/2, a 3 = a(1, 1, 0)/2 • Basis set: 2 atoms (specify element) at (000) and (¼ , ¼, ¼). Diamond: 2 identical atoms in basis (e. g. 2 C) fcc lattice

Defining the Crystal Structure • Lattice face centered cubic (fcc). • The fcc primitive lattice is generated by r = n 1 a 1+n 2 a 2+n 3 a 3 with lattice vectors: a 1 = a(0, 1, 1)/2, a 2 = a(1, 0, 1)/2, a 3 = a(1, 1, 0)/2 (NOTE: The ai’s are not mutually orthogonal!) • Basis set: 2 atoms (specify element) at (000) and (¼ , ¼, ¼). Diamond: 2 identical atoms in basis (e. g. 2 C) fcc lattice Zincblende: 2 different atoms in basis and fcc lattice For FCC 2 atom ABCABC stacking, it is called zinc blende

Close packed crystals

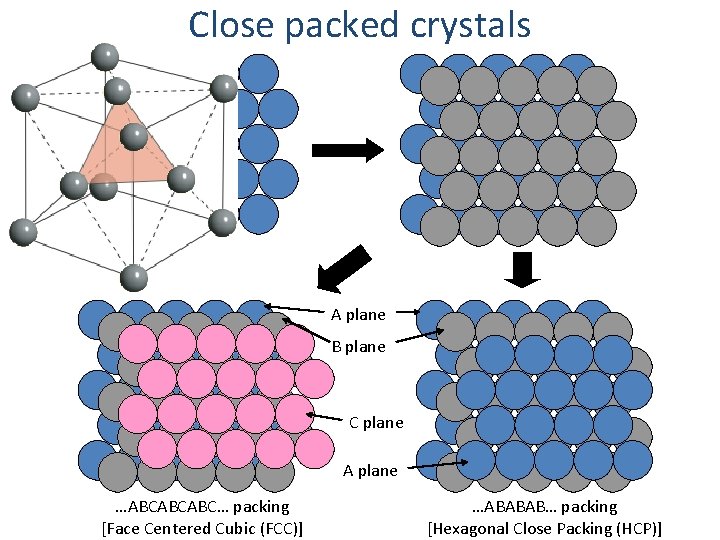
Close packed crystals A plane B plane C plane A plane …ABCABCABC… packing [Face Centered Cubic (FCC)] …ABABAB… packing [Hexagonal Close Packing (HCP)]

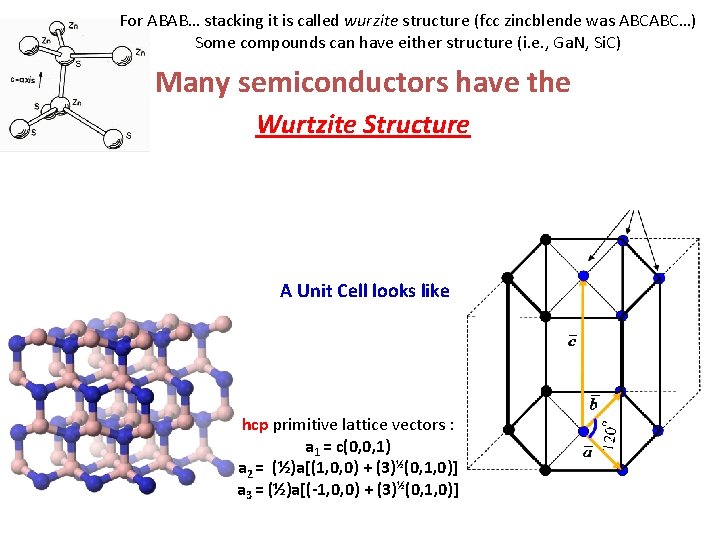
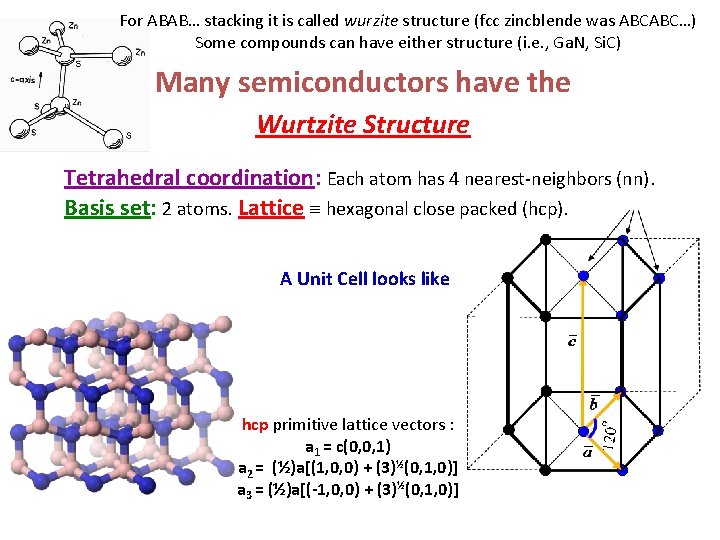
For ABAB… stacking it is called wurzite structure (fcc zincblende was ABCABC…) Some compounds can have either structure (i. e. , Ga. N, Si. C) Many semiconductors have the Wurtzite Structure

For ABAB… stacking it is called wurzite structure (fcc zincblende was ABCABC…) Some compounds can have either structure (i. e. , Ga. N, Si. C) Many semiconductors have the Wurtzite Structure A Unit Cell looks like hcp primitive lattice vectors : a 1 = c(0, 0, 1) a 2 = (½)a[(1, 0, 0) + (3)½(0, 1, 0)] a 3 = (½)a[(-1, 0, 0) + (3)½(0, 1, 0)]

For ABAB… stacking it is called wurzite structure (fcc zincblende was ABCABC…) Some compounds can have either structure (i. e. , Ga. N, Si. C) Many semiconductors have the Wurtzite Structure Tetrahedral coordination: Each atom has 4 nearest-neighbors (nn). Basis set: 2 atoms. Lattice hexagonal close packed (hcp). A Unit Cell looks like hcp primitive lattice vectors : a 1 = c(0, 0, 1) a 2 = (½)a[(1, 0, 0) + (3)½(0, 1, 0)] a 3 = (½)a[(-1, 0, 0) + (3)½(0, 1, 0)]

Ionic materials (Transferred Electron) a • In ionic materials, different considerations can be important (electrostatics, different size of ions)

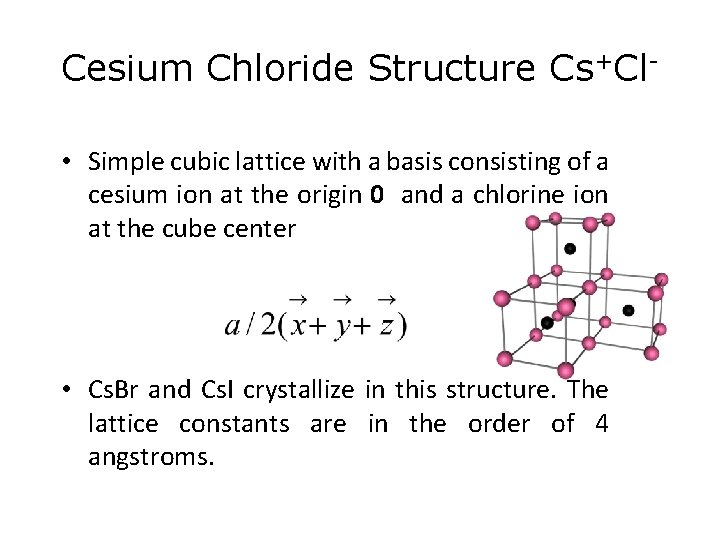
Ionic materials (Transferred Electron) • In ionic materials, different considerations can be important a (electrostatics, different size of ions) • Figure shows the crystal structure of Cs+Cl-. The lattice constant a is 4. 12 Å and all the bonds shown have the same length. The grey atoms are Cs and the green ones are Cl.

Ionic materials (Transferred Electron) • In ionic materials, different considerations can be important a (electrostatics, different size of ions) • Figure shows the crystal structure of Cs+Cl-. The lattice constant a is 4. 12 Å and all the bonds shown have the same length. The grey atoms are Cs and the green ones are Cl. • Group: Define crystal structure: meaning what are the primitive Bravais lattice and the associated basis for this crystal (including the locations of these atoms in terms of lattice parameter a)?

Cesium Chloride Structure Cs+Cl • Simple cubic lattice with a basis consisting of a cesium ion at the origin 0 and a chlorine ion at the cube center • Cs. Br and Cs. I crystallize in this structure. The lattice constants are in the order of 4 angstroms.

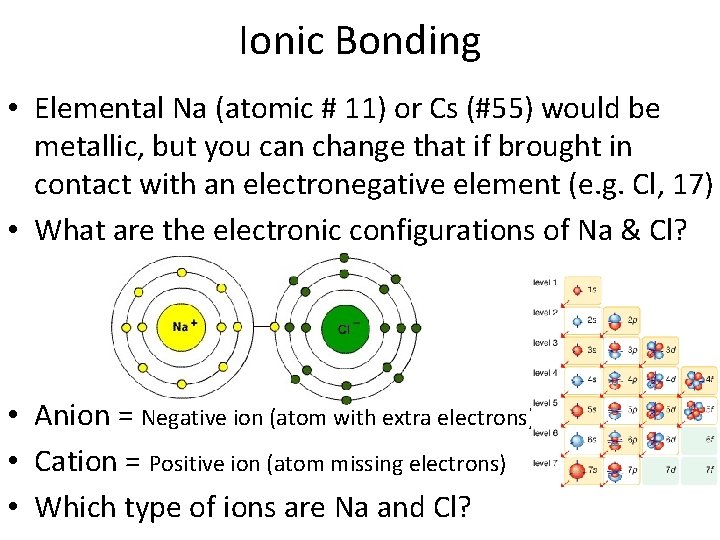
Ionic Bonding • Elemental Na (atomic # 11) or Cs (#55) would be metallic, but you can change that if brought in contact with an electronegative element (e. g. Cl, 17) • What are the electronic configurations of Na & Cl?

Ionic Bonding • Elemental Na (atomic # 11) or Cs (#55) would be metallic, but you can change that if brought in contact with an electronegative element (e. g. Cl, 17) • What are the electronic configurations of Na & Cl? • Anion = Negative ion (atom with extra electrons) • Cation = Positive ion (atom missing electrons) • Which type of ions are Na and Cl?

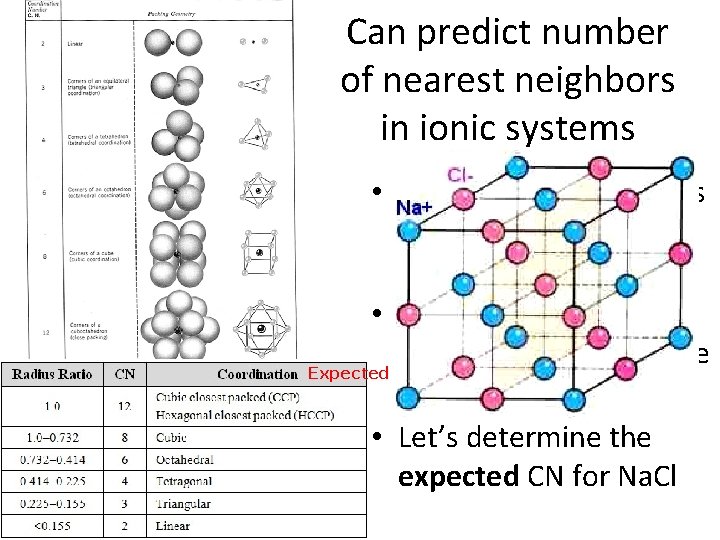
Can predict number of nearest neighbors in ionic systems • Coordination number is just the # of nearest neighbors of an ion • It varies based on the type of bonding and the Expected size of the ions. • Let’s determine the expected CN for Na. Cl