Whiteboard Mindmap WORK ENERGY POWER Energy Work Energy

Whiteboard & Mind-map: WORK, ENERGY & POWER

Energy & Work Energy – the ability to do work Work- the energy transferred to an object by an applied force over a measured distance.

W Work (Joules, J) F Force applied (N) Δd displacement (m)

Quick Practice 1) A weightlifter uses a force of 275 N to lift weights directly upward through a distance of 0. 65 m. Determine the work done on the weights by the weightlifter. 2) A pool cue stick strikes a ball with a constant force of 0. 73 N, causing the ball to move 0. 65 m in the direction of the force. The ball moves 0. 080 m while the cue stick is in contact with it. Calculate the work done on the ball by the cue stick.

θ angle between the force applied and the displacement

Quick Practice 1) A tow truck uses a winch with a rope attached to pull a car that is stuck in a ditch. The rope exerts a force of 9. 9 x 103 N on the car body, and the angle between the rope and the direction the car moves is 12°. Determine the amount of work done on the car by the tow truck to move the car 4. 3 m.

Work Case 1: Positive Work - If force applied and displacement are in the same direction Case 2: Negative Work - If force applied and displacement are in opposite directions

Case 3: Work done against gravity -if the force applied and the displacement are both vertically upward and no acceleration occurs the work done against gravity is positive Case 4: Zero Work - If force and displacement are perpendicular

Kinetic Energy – ( ) – the energy possessed by an object due to its motion From the work equation derive the kinetic energy equation

Quick Practice 1)If a bowling ball with mass 8. 0 kg travels down the lane at 2. 0 m/s, what is its kinetic energy? 2) Calculate the mass of a blue jay moving at 15 km/h with 0. 83 J of kinetic energy.

Work-Kinetic Energy Theorem

Quick Practice 1) A space probe travels far out in the galaxy to a point where the focus of gravity is very weak. The probe has a mass of 3. 8 x 104 kg and an initial speed of 1. 5 x 104 m/s. The probe’s engines exert a force of 2. 2 x 105 N in the original direction of motion as the probe travels a distance of 2. 8 x 106 m. Calculate the final speed of the probe.

Gravitational Potential Energy – ( ) – The energy possessed by an object because of its position relative to a lower position. Using the work equation derive the equation from gravitational potential energy

Quick Practice 1) A grey squirrel drops a 0. 02 kg walnut from a branch that is 8. 0 m high. Determine the change in potential energy of the walnut between the branch and the ground.
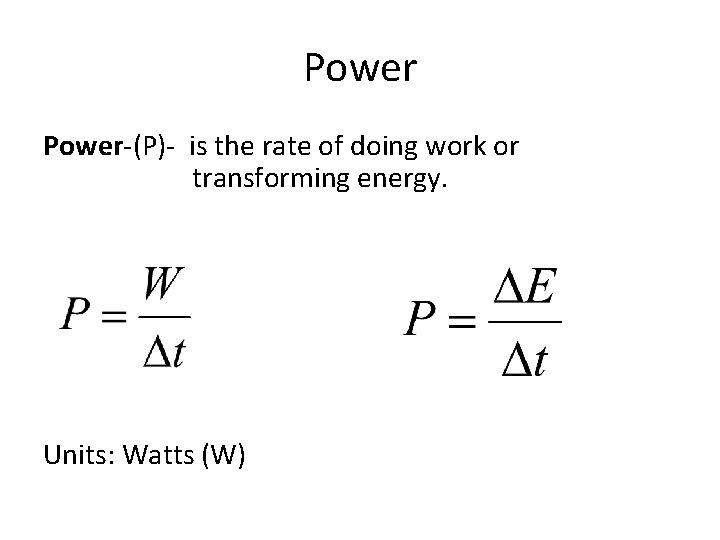
Power-(P)- is the rate of doing work or transforming energy. Units: Watts (W)

Quick Practice 1) A firefighter climbs a ladder at a speed of 1. 4 m/s. The ladder is 5. 0 m long, and the firefighter weights 65 kg. a) Determine the firefighter’s power output while climbing the ladder. b) How long does it take her to climb the ladder?

The Law of Conservation of Energy is neither created nor destroyed. It can only change form.
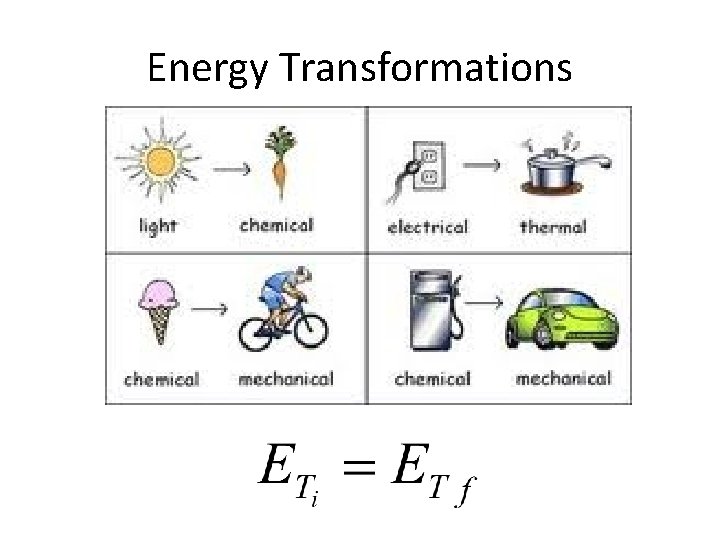
Energy Transformations

Quick Practice 1) A soccer player kicks a 0. 43 kg soccer ball down a smooth(frictionless) hill 18 m high with an initial speed of 7. 4 m/s a) Calculate the ball’s speed as it reaches the bottom of the hill b) The soccer player stands at the same point on the hill and kicks the ball at 4. 2 m/s. The ball moves up the hill, comes to a rest, and rolls back down the hill. Determine the ball’s speed as it reaches the bottom of the hill.

Hooke’s Law The amount of force exerted by a spring is directly proportional to the displacement of the spring. Spring constant –(k)- the constant of variation between the force exerted by an ideal spring and the spring’s displacement


Quick Practice 1) A 5. 3 kg mass hangs vertically from a spring with spring constant 720 N/m. The mass is lifted upward and released. Calculate the force and acceleration on the mass when the spring is compressed by 0. 36 m.

Elastic Potential Energy The elastic potential energy ( ) due to the stretching or compressing of an elastic material.

Task 1) Compare different “game” balls. Which “game” ball stores the most energy. 2) Make a jumping device. It must store potential energy and lift itself and all its contents (no water rockets!) to the greatest possible height.

Quick Practice 1) A spring-loaded toy uses a compressed spring to fire a marble out of a tube. A force of 220 N compressed the spring by 0. 14 m. Calculate the elastic potential energy of the toy.

Motion Periodic Motion – motion that repeats in equal time intervals Simple Harmonic Motion (SHM) - periodic motion in which the acceleration of the moving object is proportional to its displacement

Period of a mass on a spring

SHM video SHM and circular motion video SHM review Making connections investigation

Quick Practice 1) A 105 kg swimmer stands on a diving board with a spring constant of 7. 6 x 103 N/m. Determine the period and frequency of the board vibrations.

Springs and Conservation of Energy Quick Practice 1) A block with a mass of 2. 0 kg is held against a spring with spring constant 250 N/m. The block compresses the spring 22 cm from its equilibrium position. After the block is released , it travels along a frictionless surface and then up a frictionless ramp. The ramp’s angle of inclination is 30°. a) Determine the elastic potential energy stored in the spring before the mass is released. b) Calculate the speed of the block as it travels along the horizontal surface c) Determine how far along the ramp the block will travel before it stops.

Motion Machines Perpetual Motion Machines – a machine that can operate forever without restarting or refueling. Video
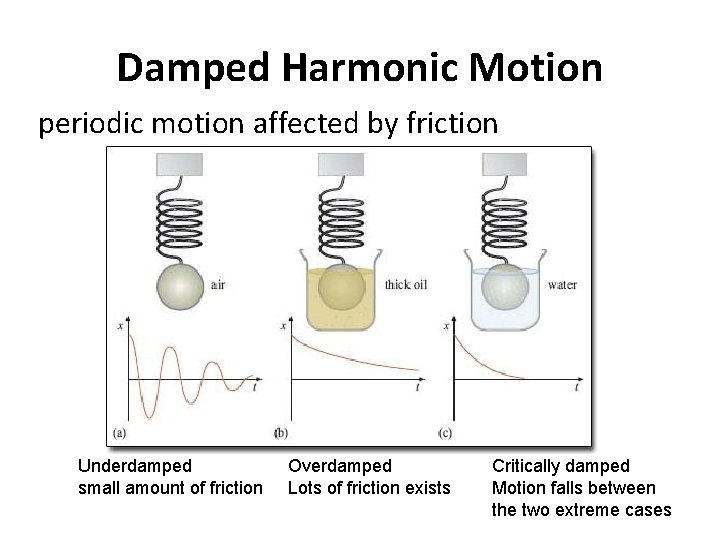
Damped Harmonic Motion periodic motion affected by friction Underdamped small amount of friction Overdamped Lots of friction exists Critically damped Motion falls between the two extreme cases

Momentum & Collisions

Momentum Linear Momentum – ( ) a quantity that describes the motion of an object travelling in a straight line as the product of its mass and velocity Bill Nye Video Momentum of Rockets

Quick Practice 1) Calculate the momentum and kinetic energy of a hockey puck with a mass of 160 g travelling with a velocity of 40. 0 m/s[E].
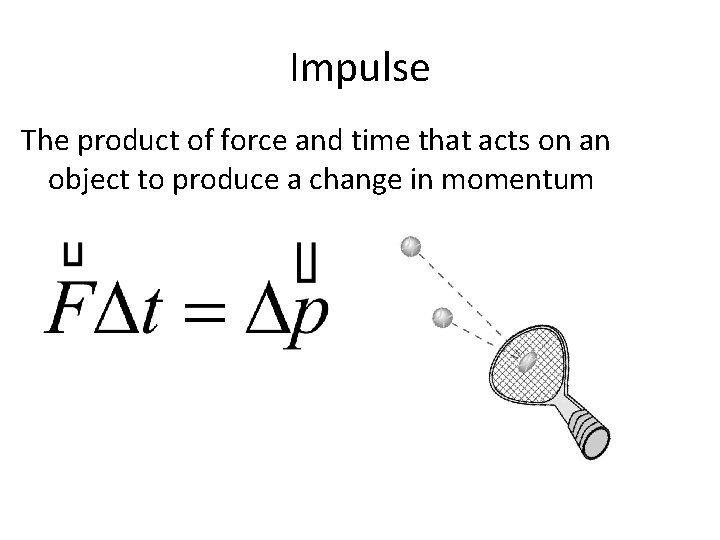
Impulse The product of force and time that acts on an object to produce a change in momentum
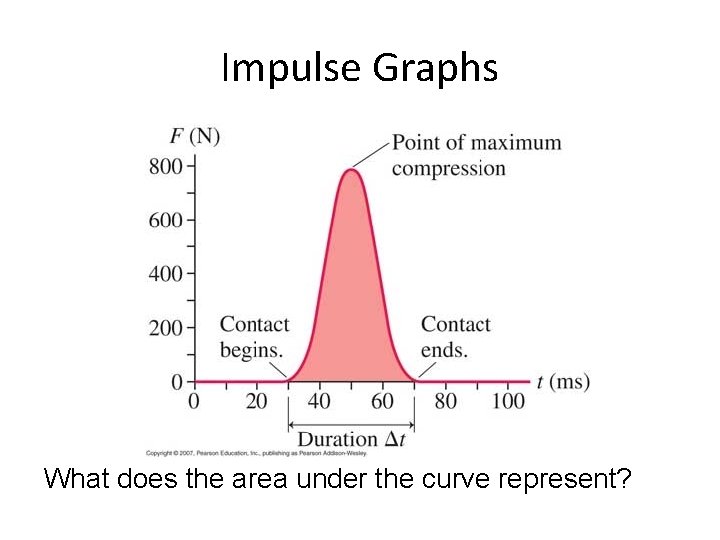
Impulse Graphs What does the area under the curve represent?

Quick Question 1) A hockey player passes a puck with an average force of 250 N. The hockey stick is in contact with the puck for 0. 0030 s, and its mass of the puck is 180 g. The puck is not moving before the player passes it. a) Determine the impulse imparted by the hockey stick. b) Calculate the momentum of the puck as a result of this collision.

Law of Conservation of Momentum When two or more objects collide, the collision does not change the total momentum of the two objects. Whatever momentum is lost by one object in the collision is gained by the other. The total momentum of the system is conserved. Newton’s Cradle
![Quick Practice 1) A 1350 kg car travelling at 72 km/h[S] collides with a Quick Practice 1) A 1350 kg car travelling at 72 km/h[S] collides with a](http://slidetodoc.com/presentation_image_h2/0462fb68e3431c730658c5a0a396df30/image-41.jpg)
Quick Practice 1) A 1350 kg car travelling at 72 km/h[S] collides with a slow moving car of mass 1650 kg, also initially travelling south. After the collision, the velocity of the two cars together is 24 km/h[S]. Determine the initial velocity at which the second car was travelling.

Collisions Elastic – a collision in which momentum and kinetic energy are conserved Inelastic – a collision in which momentum is conserved, but kinetic energy is not conserved

Conservation of Kinetic Energy The total kinetic energy of two objects before a collision is equal to the total kinetic energy of the two objects after the collision.

Collisions continued Perfectly elastic – an ideal collision in which external forces are minimized to the point where momentum and kinetic energy are perfectly conserved Perfectly inelastic – an ideal collision in which two objects stick together perfectly so they have the same final velocity; in this situation momentum is perfectly conserved, but kinetic energy is not conserved

Quick Practice 1) Two balls collide in a perfectly elastic collision. Ball 1 has mass 3. 5 kg and is initially travelling at a velocity of 5. 4 m/s[right]. It collides head on with a stationary ball 2 with mass 4. 8 kg. Determine the final velocity of ball 2. 2) A 66 kg snowboarder slides down a hill 25 m high and has a perfectly inelastic collision with an initially stationary 72 kg skier at the bottom of the hill. Friction is negligible. Calculate the speed of each person after the collision.

Head-On Elastic Collisions 1 D Determine the general equations for the cases below: Case 1: Objects have the same mass Case 2: Lighter object colliding with a heavier stationary object

Quick Questions 1) A ball of mass 80. 0 g is moving at 7. 0 m/s[W] when it undergoes a head on collision with a stationary ball of mass 60. 0 g. Assume the collision is 1 D. Calculate the velocity of each ball after the collision.

Quick Question 1) A dynamics cart 1 ahs a mass of 1. 8 kg and is moving with a velocity of 4. 0 m/s[right] along a frictionless track. Dynamics cart 2 has a mass of 2. 2 kg and is moving at 6. 0 m/s[left]. The carts collide in a head-on elastic collision cushioned by a spring with spring constant k = 8. 0 x 104 N/m. a) Determine the compression of the spring in cm, during the collision when cart 2 is moving at 4. 0 m/s[left] b) Calculate the maximum compression of the spring in cm

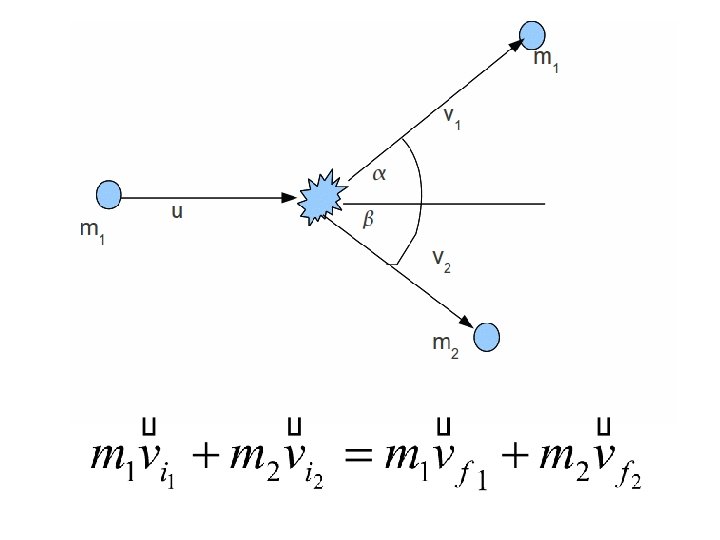
Collision in 2 D Glancing collisions – a collision in which the first object, after an impact with the second object, travels at an angle to the direction it was originally travelling.

Quick Question 1) Two freight trains have a completely inelastic collision at a track crossing. Engine 1 has a mass of 1. 4 x 104 kg and is initially travelling at 45 km/h[N]. Engine 2 has a mass of 1. 5 x 104 kg and is initially travelling at 53 km/h[W]. Calculate the final velocity.

Quick Practice 2)Two hockey pucks of equal mass approach each other. Puck 1 has an initial velocity of 20. 0 m/s [S 45°E], and puck 2 has an initial velocity of 15 m/s[S 45°W]. After the collision, the first puck is moving with a velocity of 10 m/s [S 45°W]. a) Determine the final velocity of the second puck. b) Is this collision elastic , perfectly inelastic or non-perfectly inelastic? Explain.
- Slides: 51