White Clear Box Testing Verilog code is available

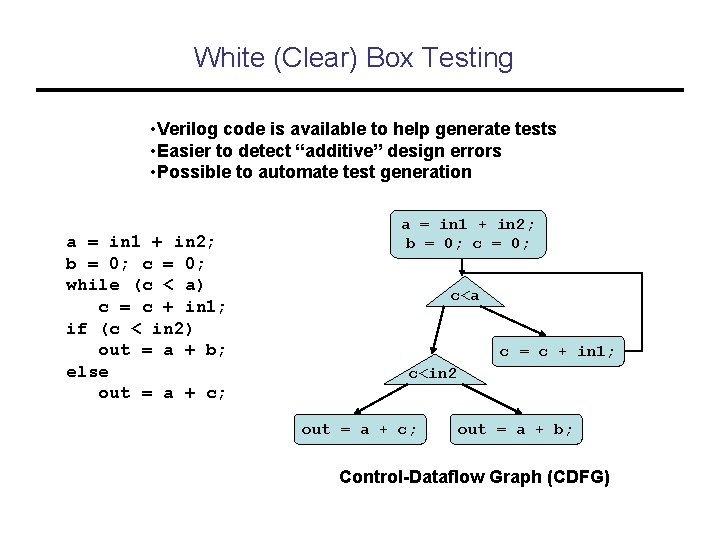
White (Clear) Box Testing • Verilog code is available to help generate tests • Easier to detect “additive” design errors • Possible to automate test generation a = in 1 + in 2; b = 0; c = 0; while (c < a) c = c + in 1; if (c < in 2) out = a + b; else out = a + c; a = in 1 + in 2; b = 0; c<a c = c + in 1; c<in 2 out = a + c; out = a + b; Control-Dataflow Graph (CDFG)

Code Coverage Metrics • • • Coverage metric is a numerical measurement of the adequacy of an arbitrary test set for validation. High coverage is a goal for test generation The measure is based on code execution 1. Statement coverage - Fraction of statements executed 2. Branch coverage - Fraction of branch directions executed 3. Path coverage - Fraction of control-flow paths executed

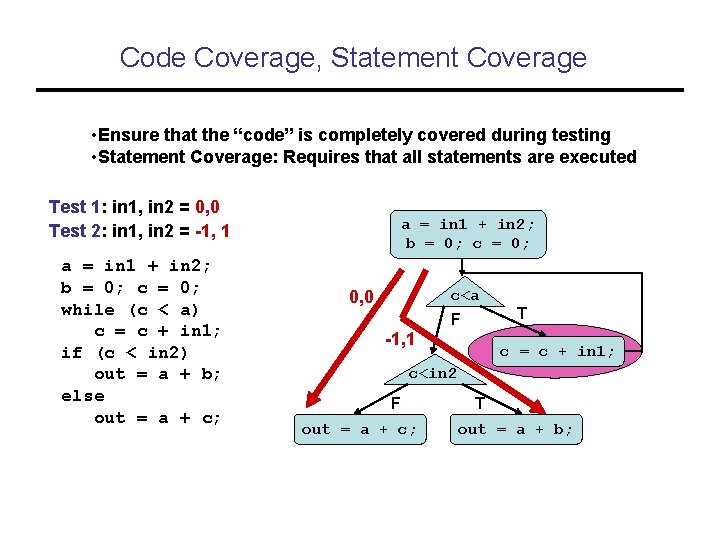
Code Coverage, Statement Coverage • Ensure that the “code” is completely covered during testing • Statement Coverage: Requires that all statements are executed Test 1: in 1, in 2 = 0, 0 Test 2: in 1, in 2 = -1, 1 a = in 1 + in 2; b = 0; c = 0; while (c < a) c = c + in 1; if (c < in 2) out = a + b; else out = a + c; a = in 1 + in 2; b = 0; c<a 0, 0 T F -1, 1 c = c + in 1; c<in 2 F out = a + c; T out = a + b;

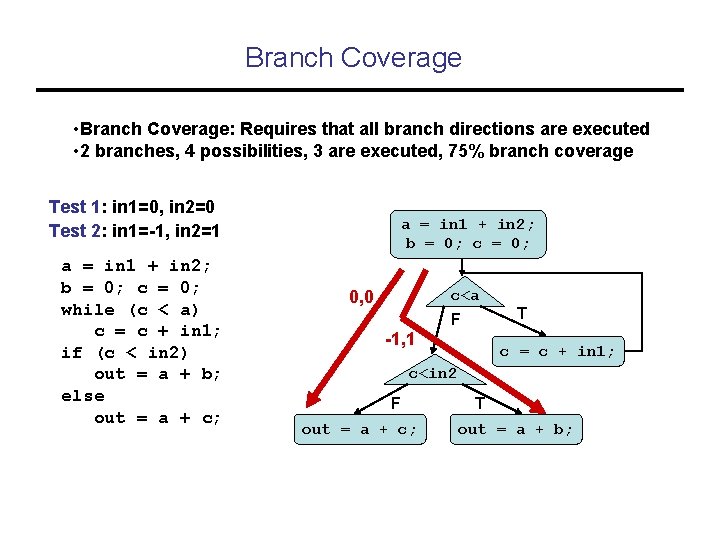
Branch Coverage • Branch Coverage: Requires that all branch directions are executed • 2 branches, 4 possibilities, 3 are executed, 75% branch coverage Test 1: in 1=0, in 2=0 Test 2: in 1=-1, in 2=1 a = in 1 + in 2; b = 0; c = 0; while (c < a) c = c + in 1; if (c < in 2) out = a + b; else out = a + c; a = in 1 + in 2; b = 0; c<a 0, 0 T F -1, 1 c = c + in 1; c<in 2 F out = a + c; T out = a + b;

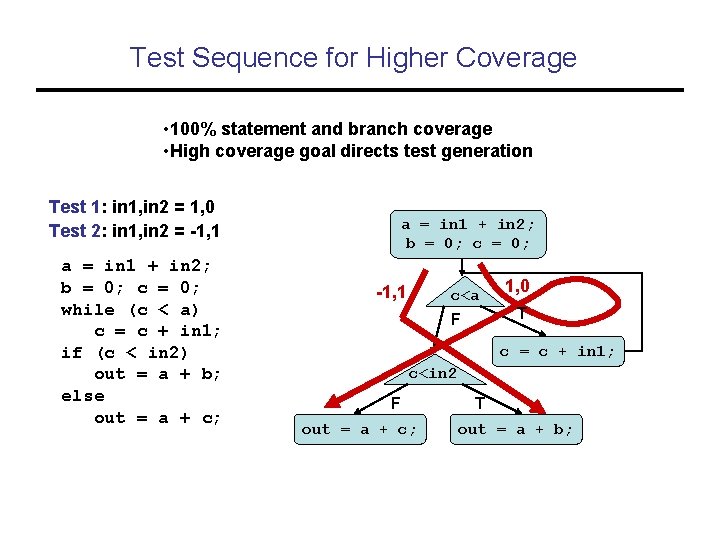
Test Sequence for Higher Coverage • 100% statement and branch coverage • High coverage goal directs test generation Test 1: in 1, in 2 = 1, 0 Test 2: in 1, in 2 = -1, 1 a = in 1 + in 2; b = 0; c = 0; while (c < a) c = c + in 1; if (c < in 2) out = a + b; else out = a + c; a = in 1 + in 2; b = 0; c = 0; -1, 1 c<a 1, 0 T F c = c + in 1; c<in 2 F out = a + c; T out = a + b;

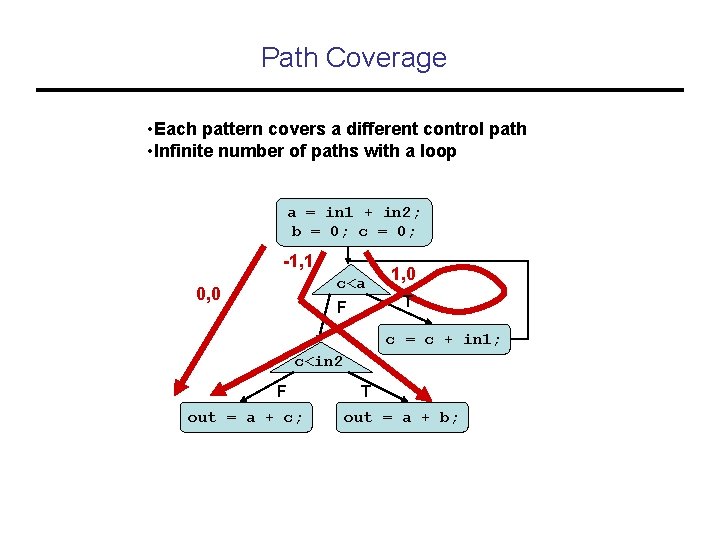
Path Coverage • Each pattern covers a different control path • Infinite number of paths with a loop a = in 1 + in 2; b = 0; c = 0; -1, 1 c<a 0, 0 1, 0 T F c = c + in 1; c<in 2 F out = a + c; T out = a + b;

Domain (Boundary) Coverage • Each conditional predicate defines partitions the input space • A small error may move the partition foo (in 1, in 2) if (in 1 < in 2) out = 1; else out = 0; out=1 in 2 out=0 in 1 • What if in 1 < in 2 should be in 1 <= in 2? • What if in 1 or in 2 has a slightly incorrect value?

Domain Test Goal • Test with input data on the boundary and just on either side of the boundary foo (in 1, in 2) if (in 1 < in 2) out = 1; else out = 0; in 2 out=1 out=0 2 1 1 in 1 • Test 1: in 1, in 2 = 1, 1 - False, on the boundary • Test 2: in 1, in 2 = 1, 2 - True, just off the boundary

Domain Test Example • Need to satisfy 2 conditions for each predicate: q. True and near-boundary q. False and near-boundary a = in 1 + in 2; b = 0; c = 0; while (c < a) c = c + in 1; if (c < in 2) out = a + b; else out = a + c; Test 1: in 1, in 2 = 0, 0 • Sets c = 0, and a = 0 • False and on-boundary for c < a • False and on-boundary for c < in 2 Test 2: in 1, in 2 = 1, 0 • Sets c = 0, and a = 0 • True and near-boundary for c < a • c set to 1 in loop • False and on-boundary for c < in 2 • 3 of 4 conditions satisfied, 75% coverage

Domain Test Complications • Non-standard Domain Boundaries Piecewise Linear Boundaries: Test each linear piece separately (in 2 > in 1) and (in 1 > 2) in 2 2 in 1 Higher Degree Boundaries: No standard solution (in 2 > in 12) in 2 in 1

Coverage Metrics as Test Constraints • Coverage metrics provide constraints which can be used to evaluate the completeness of testing • Testing is complete when all constraints are satisfied Uses of Test Constraints: q. Evaluation of Test Sequence - “Does this test sequence satisfy all constraints? ” q. Directing Test Generation - “Given these constraints, create a test sequence which satisfies them. ”

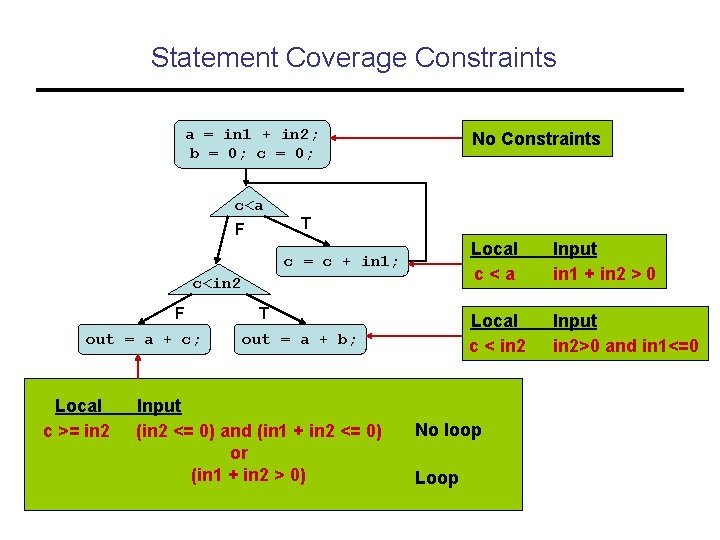
Statement Coverage Constraints a = in 1 + in 2; b = 0; c = 0; No Constraints c<a T F c = c + in 1; c<in 2 F out = a + c; Local c >= in 2 T out = a + b; Input (in 2 <= 0) and (in 1 + in 2 <= 0) or (in 1 + in 2 > 0) Local c<a Input in 1 + in 2 > 0 Local c < in 2 Input in 2>0 and in 1<=0 No loop Loop

Tests for Statement Coverage a = in 1 + in 2; b = 0; c = 0; • 0, 0 satisfies test constraints for out=a+c c<a 0, 0 T F -1, 1 c = c + in 1; c<in 2 F T out = a + c; out = a + b; (in 2 <= 0) and (in 1 + in 2 <= 0) (in 2 > 0) and (in 1 <= 0) • -1, 1 satisfies test constraints for out=a+b;

Optimism in a Coverage Metric • 100% statement coverage does not guarantee error detection • Test constraints may not be the same as detection constraints a = in 1 + in 2; b = 0; c = 0; while (c < a) c = c + in 1; if (c < in 2) out = a + b; else out = a + c; Erroneous statement out = a - c; • Test 0, 0 executes erroneous statement but does not detect the error • Detection constraint includes a - c != a + c

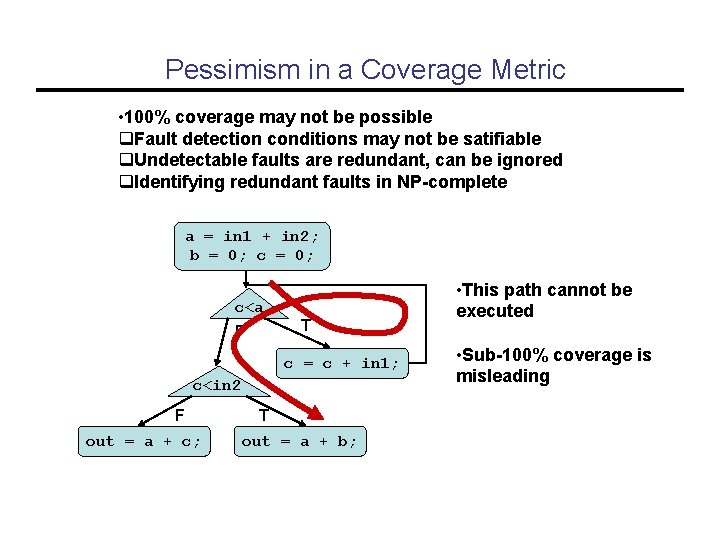
Pessimism in a Coverage Metric • 100% coverage may not be possible q. Fault detection conditions may not be satifiable q. Undetectable faults are redundant, can be ignored q. Identifying redundant faults in NP-complete a = in 1 + in 2; b = 0; c<a T F c = c + in 1; c<in 2 F out = a + c; T out = a + b; • This path cannot be executed • Sub-100% coverage is misleading