Which Regular Expression Patterns are Hard to Match


















- Slides: 26

Which Regular Expression Patterns are Hard to Match? Arturs Backurs Piotr Indyk 2015 - Dec - 01 (0|1 … 9)+ - (a|b … z|A|B … Z)+ - (0|1 … 9)+ 1

Regular expressions • Regular expression (regexp) describes a set of sequences • Example: (x | yy)+ → {x, yy, xx, xyy, yyx, yyyy, yyxyy, …} • Regexp consists of individual symbols and operators • Concatenation ◦ • Or | • Kleene star * x◦y◦y xy | xyy | yyyy → {xyy} → {xy, xyy, yyyy} (xyy)* → {ε, xyyxyy, xyyxyyxyy, …} (xyy)+ → {xyy, xyyxyyxyy, …} • Kleene plus + 2

Regular expression membership • Pattern p (regexp) • Text t (sequence of symbols) • Can t be derived from p? p=(0|1 … 9)+ - (a|b … z|A|B … Z)+ - (0|1 … 9)+ t=2000 -Jan-01 t=2000 -Jan 3

Regular expression membership • Given pattern p and text t • We can solve regexp membership in time O(|p| · |t|) • Nondeterministic automata for p of size O(|p|) • Read symbols of t one by one • Maintain set of reachable states of the automata • Runtime can be improved to O(|p| · |t| · log |t| / log 3/2|t|) [Myers’ 92, Bille-Thorup’ 09] 4

Regular expression pattern matching • Pattern p • Text t • Is there a substring of t that can be derived from p? p=(0|1 … 9)+ - (a|b … z|A|B … Z)+ - (0|1 … 9)+ t=aaaaaa 2000 -Jan-01 a 2001 -Feb- • Can be solved in time O(|p| · |t| · log |t| / log 3/2|t|) [Myers’ 92, Bille-Thorup’ 09] 5

Regular expressions: applications • Computational primitive in Perl, Python, Java. Script, Ruby, AWK, Tcl and Google RE 2 • Computer networks • Databases and data mining • Human-computer interaction • … 6

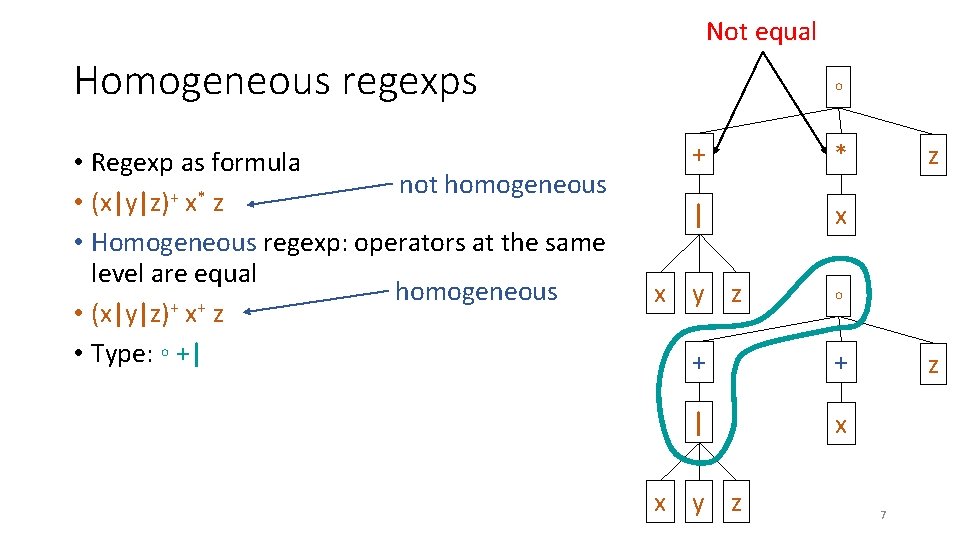
Not equal Homogeneous regexps • Regexp as formula not homogeneous + * • (x|y|z) x z • Homogeneous regexp: operators at the same level are equal homogeneous + + • (x|y|z) x z • Type: ◦ +| ◦ + * | x x y z ◦ + + | x x y z z z 7

Examples of homogeneous regexp matching • Type ◦ | regexp matching • Example: (a|b|c)b(c|a|d) • Special case of Superset Matching problem • Can be solved in nearly linear time [Cole-Hariharan’ 02] • Type | ◦ regexp matching • Example: abc|bcddd|ba • Dictionary Matching problem • Can be solved in linear time [Aho-Corasick’ 75] 8

Our results: Classification of homogeneous regexps • Dichotomy: regexp matching is either easy (near-linear time) or SETH-hard • Depth-2 homogeneous regexp matching • All depth-2 types are in nearly linear time, except ◦ * • More details in the next slide • Depth-3 regexp matching • 13 types require nearly quadratic time (assuming SETH) • More details later in the talk ◦+ |◦ *◦ +◦ ◦* |* *+ +| ◦| |+ *| +* ◦|◦ |◦| *|◦ +◦| ◦|* |◦+ *|* +◦+ ◦|+ |◦* *|+ +◦* ◦+◦ |*◦ *+◦ +|◦ ◦+* |*| *+| +|* ◦+| |*+ *+* +|+ ◦*◦ |+◦ *◦* +*◦ ◦*+ |+* *◦| +*+ ◦*| |+| *◦+ 9 +*|

Our results: Classification of homogeneous regexps • Depth-2 regexp matching: our results • Type ◦ + regexps ◦+ |◦ *◦ +◦ ◦* |* *+ +| ◦| |+ *| +* easy hard trivial • Example: xyy+x+x+xyx+ • Can be solved in nearly linear time (reduction to Subset Matching and Wildcard Matching) • Type ◦ * regexps • Example: xyy*x*x*xyx* • Requires nearly quadratic time (assuming SETH) • Sketch of the proof: later in the talk • Type ◦ | and | ◦, and + ◦ can be solved in nearly linear time (prior work) • Other depth-2 regexps: linear time trivial solutions 10

Our results: Classification of homogeneous regexps • Depth-3 regexps • 36 types in total • 30 types can be reduced to depth-2 types +| ◦ reduces to | ◦ can be solved in linear time (x | yy) yy + • Example: | ◦ * is hard since ◦ * requires nearly quadratic time • Example: • 6 types require nearly quadratic time (assuming SETH) • See the paper for the proofs • All depth-4, 5, … regexps can be reduced to depth-3 regexps ◦|◦ |◦| *|◦ +◦| ◦|* |◦+ *|* +◦+ ◦|+ |◦* *|+ +◦* ◦+◦ |*◦ *+◦ +|◦ ◦+* |*| *+| +|* ◦+| |*+ *+* +|+ ◦*◦ |+◦ *◦* +*◦ ◦*+ |+* *◦| +*+ ◦*| |+| *◦+ +*| easy – reducible to depth 2 hard – needs a proof 11

Hardness for type ◦ * Theorem. No (|pattern|·|text|). 99 algorithm for ◦ * matching unless SETH fails • SETH (Strong Exponential Time Hypothesis). CNF-SAT problem can’t be solved in 1. 99#Variables time • For the rest of the talk: |pattern|=|text|=L 12

Orthogonal Vectors Conjecture L=|pattern|=|text| Theorem. No L 1. 99 algorithm for ◦ * matching unless Orthogonal Vectors Conjecture fails • Orthogonal Vectors Problem. Given two sets of vectors A, B⊆ {0, 1}d, |A|=|B|=n, determine whethere a ∈ A, b ∈ B such that Σi=1 daibi=0 • Orthogonal Vectors Problem can be solved trivially in O(n 2 d) time • Best known algorithm runs in n 2 -Ω(1/log c(n)) time, where d=c(n)·log n [Abboud-Williams-Yu’ 15] • n 1. 99·d. O(1) time algorithm for this problem? 13

Orthogonal Vectors Conjecture L=|pattern|=|text| Theorem. No L 1. 99 algorithm for ◦ * matching unless Orthogonal Vectors Conjecture fails • Orthogonal Vectors Problem. Given two sets of vectors A, B⊆ {0, 1}d, |A|=|B|=n, determine whethere a ∈ A, b ∈ B such that Σi=1 daibi=0 • Orthogonal Vectors Conjecture. There is no n 1. 99·d. O(1) time algorithm that solves Orthogonal Vectors Problem • Orthogonal Vectors Conjecture is implied by SETH [Williams’ 04] • For the rest of the talk, think d=polylog n 14

High level idea • A⊆{0, 1}d → pattern p, |p|=L ≤O(n·d) • B⊆{0, 1}d → text t, |t|=L ≤O(n·d) • If exists a ∈ A, b ∈ B with Σiaibi =0, a substring of t can be derived from p • Otherwise, no substring of t can be derived from p • The construction time is O(n·d) • Theorem. If ◦ * matching can be solved in L 1. 99 time, then Orthogonal Vectors Conjecture is false L=|pattern|=|text| 15

Simplifying assumptions • Orthogonal Vectors Problem. Given two sets of vectors A={a 1…an}, B={b 1…bn} ⊆ {0, 1}d, determine whethere a ∈ A, b ∈ B such that Σi=1 daibi=0 • n is odd • d≥ 100 • Orthogonal vectors ai and bj satisfy i≡j(mod 2) (assuming are two orthogonal vectors) • b 1=bd=0 for all b ∈ B • a 1 is not orthogonal to any vector from B 16

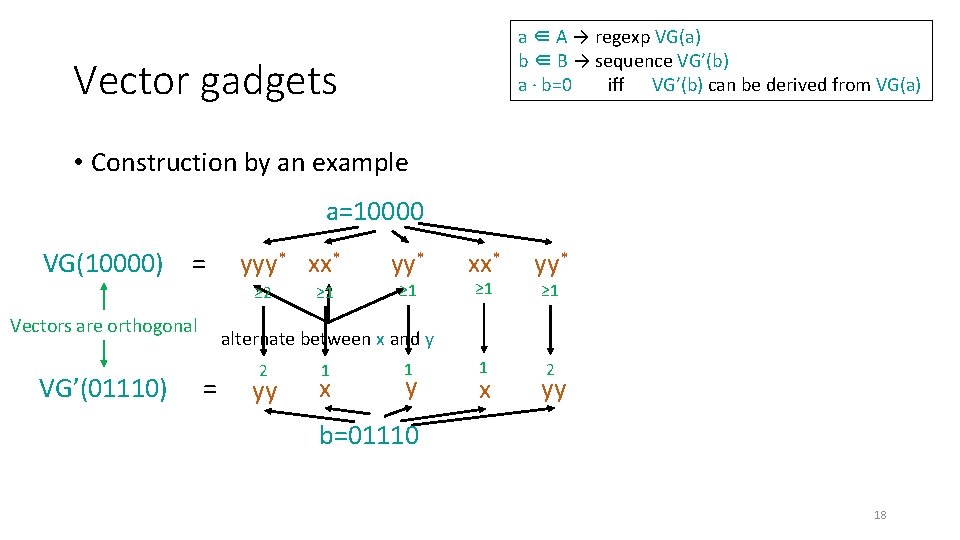
Vector gadgets • a ∈ A → regexp VG(a) |VG(a)|≤O(d) • b ∈ B → sequence VG’(b) |VG’(b)|≤O(d) • If a and b are orthogonal, then VG’(b) can be derived from VG(a) • If a and b are NOT orthogonal, then VG’(b) can’t be derived from VG(a) 17

a ∈ A → regexp VG(a) b ∈ B → sequence VG’(b) a · b=0 iff VG’(b) can be derived from VG(a) Vector gadgets • Construction by an example a=10000 VG(10000) = yyy* xx* ≥ 2 Vectors are orthogonal VG’(01110) ≥ 1 yy* ≥ 1 xx* yy* 1 2 ≥ 1 alternate between x and y = 2 yy 1 x 1 y x yy b=01110 18

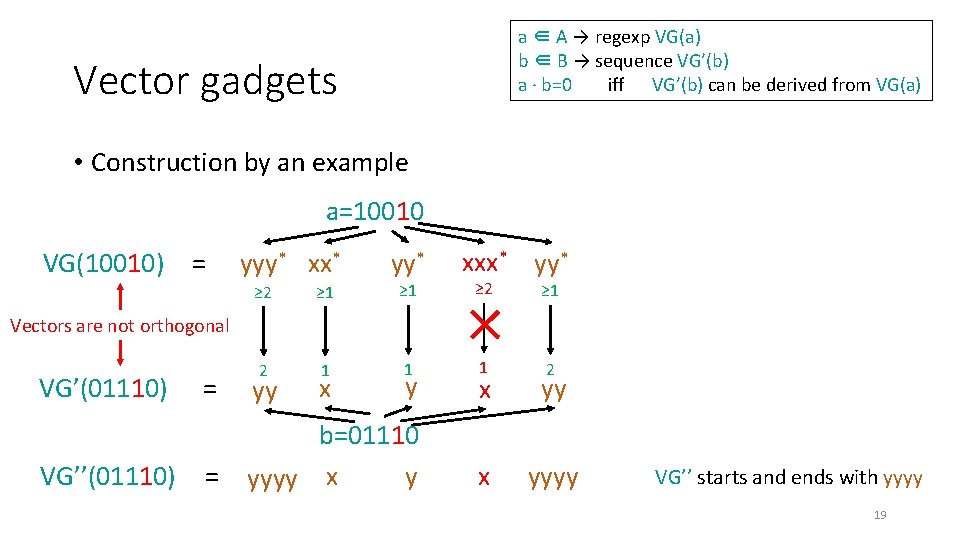
a ∈ A → regexp VG(a) b ∈ B → sequence VG’(b) a · b=0 iff VG’(b) can be derived from VG(a) Vector gadgets • Construction by an example a=10010 VG(10010) = yyy* xx* yy* ≥ 2 ≥ 1 2 1 1 xxx* yy* ≥ 2 ≥ 1 1 2 Vectors are not orthogonal VG’(01110) VG’’(01110) = yy y x yy = b=01110 y yyyy x x yyyy x VG’’ starts and ends with yyyy 19

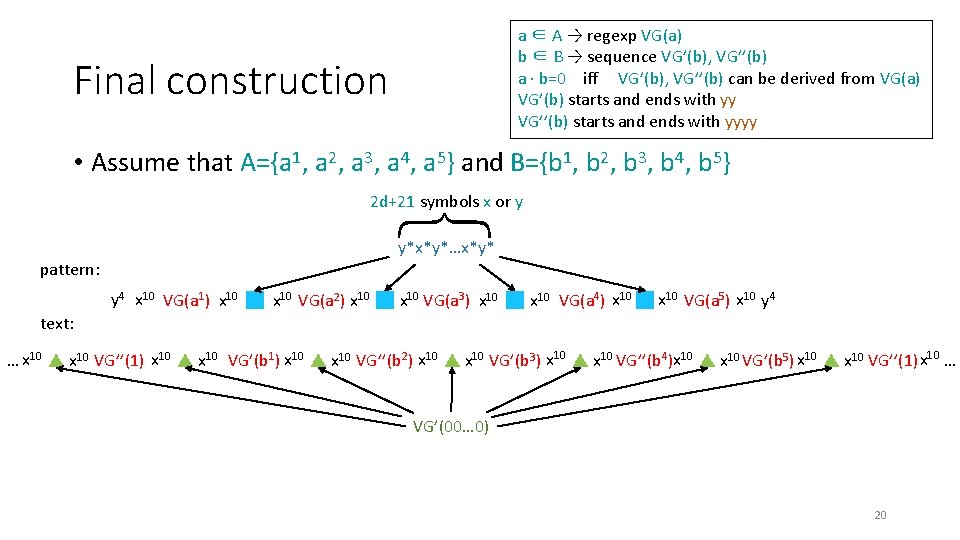
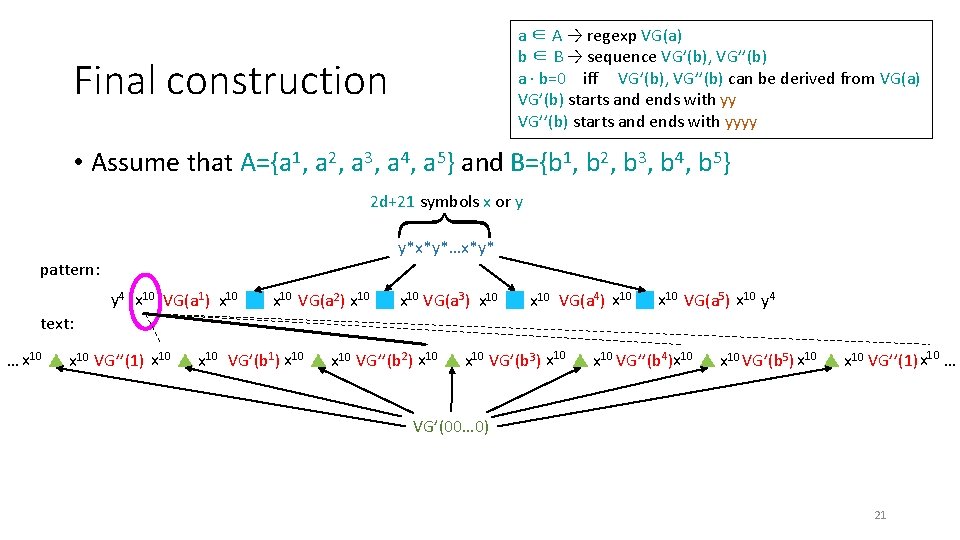
a ∈ A → regexp VG(a) b ∈ B → sequence VG’(b), VG’’(b) a · b=0 iff VG’(b), VG’’(b) can be derived from VG(a) VG’(b) starts and ends with yy VG’’(b) starts and ends with yyyy Final construction • Assume that A={a 1, a 2, a 3, a 4, a 5} and B={b 1, b 2, b 3, b 4, b 5} { 2 d+21 symbols x or y y*x*y*…x*y* pattern: y 4 x 10 VG(a 1) x 10 VG(a 2) x 10 VG(a 3) x 10 VG(a 4) x 10 VG(a 5) x 10 y 4 text: … x 10 VG’’(1) x 10 VG’(b 1) x 10 VG’’(b 2) x 10 VG’(b 3) x 10 VG’’(b 4)x 10 VG’(b 5) x 10 VG’’(1) x 10 … VG’(00… 0) 20

a ∈ A → regexp VG(a) b ∈ B → sequence VG’(b), VG’’(b) a · b=0 iff VG’(b), VG’’(b) can be derived from VG(a) VG’(b) starts and ends with yy VG’’(b) starts and ends with yyyy Final construction • Assume that A={a 1, a 2, a 3, a 4, a 5} and B={b 1, b 2, b 3, b 4, b 5} { 2 d+21 symbols x or y y*x*y*…x*y* pattern: y 4 x 10 VG(a 1) x 10 VG(a 2) x 10 VG(a 3) x 10 VG(a 4) x 10 VG(a 5) x 10 y 4 text: … x 10 VG’’(1) x 10 VG’(b 1) x 10 VG’’(b 2) x 10 VG’(b 3) x 10 VG’’(b 4)x 10 VG’(b 5) x 10 VG’’(1) x 10 … VG’(00… 0) 21

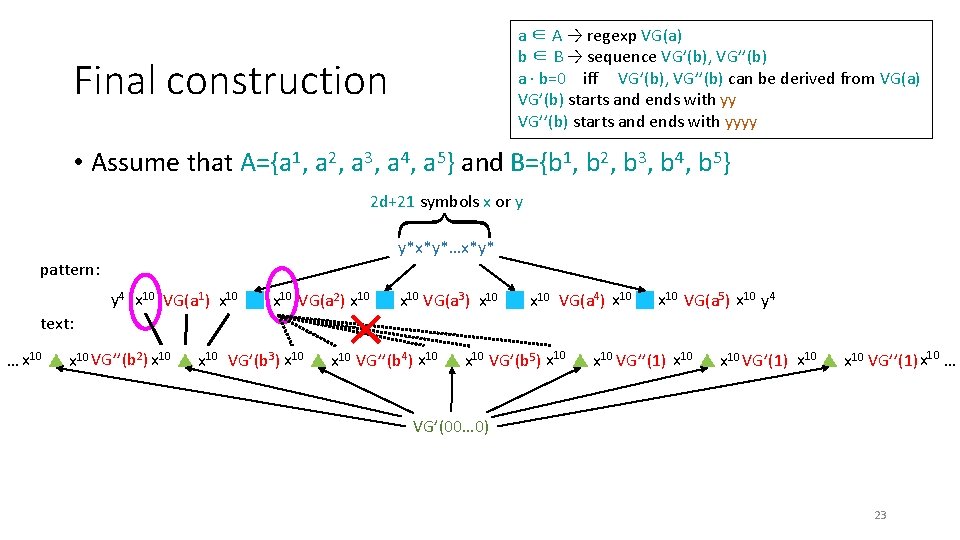
a ∈ A → regexp VG(a) b ∈ B → sequence VG’(b), VG’’(b) a · b=0 iff VG’(b), VG’’(b) can be derived from VG(a) VG’(b) starts and ends with yy VG’’(b) starts and ends with yyyy Final construction • Assume that A={a 1, a 2, a 3, a 4, a 5} and B={b 1, b 2, b 3, b 4, b 5} { 2 d+21 symbols x or y y*x*y*…x*y* pattern: y 4 x 10 VG(a 1) x 10 VG(a 2) x 10 VG(a 3) x 10 VG(a 4) x 10 VG(a 5) x 10 y 4 text: … x 10 VG’’(1) x 10 VG’(b 1) x 10 VG’’(b 2) x 10 VG’(b 3) x 10 VG’’(b 4)x 10 VG’(b 5) x 10 VG’’(1) x 10 22

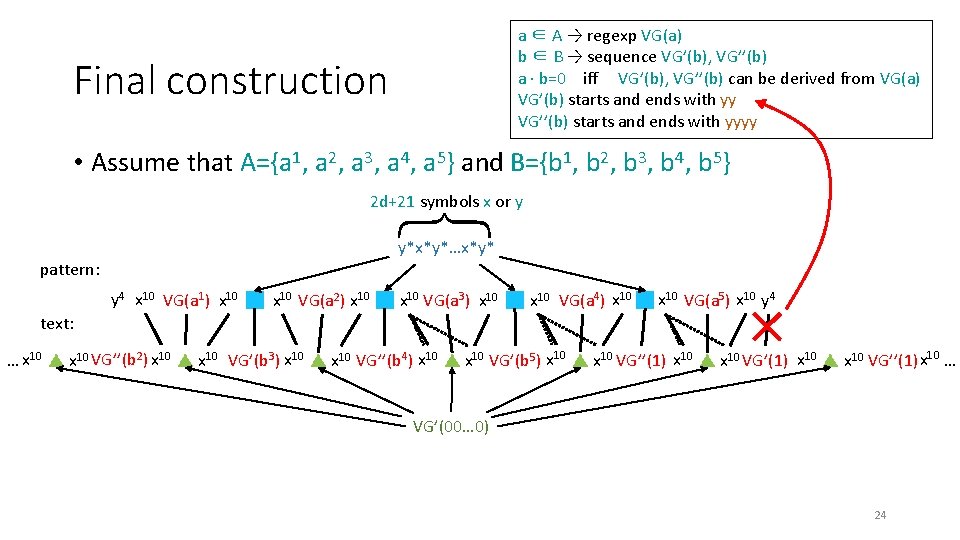
a ∈ A → regexp VG(a) b ∈ B → sequence VG’(b), VG’’(b) a · b=0 iff VG’(b), VG’’(b) can be derived from VG(a) VG’(b) starts and ends with yy VG’’(b) starts and ends with yyyy Final construction • Assume that A={a 1, a 2, a 3, a 4, a 5} and B={b 1, b 2, b 3, b 4, b 5} { 2 d+21 symbols x or y y*x*y*…x*y* pattern: y 4 x 10 VG(a 1) x 10 VG(a 2) x 10 VG(a 3) x 10 VG(a 4) x 10 VG(a 5) x 10 y 4 text: … x 10 VG’’(b 2) x 10 VG’(b 3) x 10 VG’’(b 4) x 10 VG’(b 5) x 10 VG’’(1) x 10 … VG’(00… 0) 23

a ∈ A → regexp VG(a) b ∈ B → sequence VG’(b), VG’’(b) a · b=0 iff VG’(b), VG’’(b) can be derived from VG(a) VG’(b) starts and ends with yy VG’’(b) starts and ends with yyyy Final construction • Assume that A={a 1, a 2, a 3, a 4, a 5} and B={b 1, b 2, b 3, b 4, b 5} { 2 d+21 symbols x or y y*x*y*…x*y* pattern: y 4 x 10 VG(a 1) x 10 VG(a 2) x 10 VG(a 3) x 10 VG(a 4) x 10 VG(a 5) x 10 y 4 text: … x 10 VG’’(b 2) x 10 VG’(b 3) x 10 VG’’(b 4) x 10 VG’(b 5) x 10 VG’’(1) x 10 … VG’(00… 0) 24

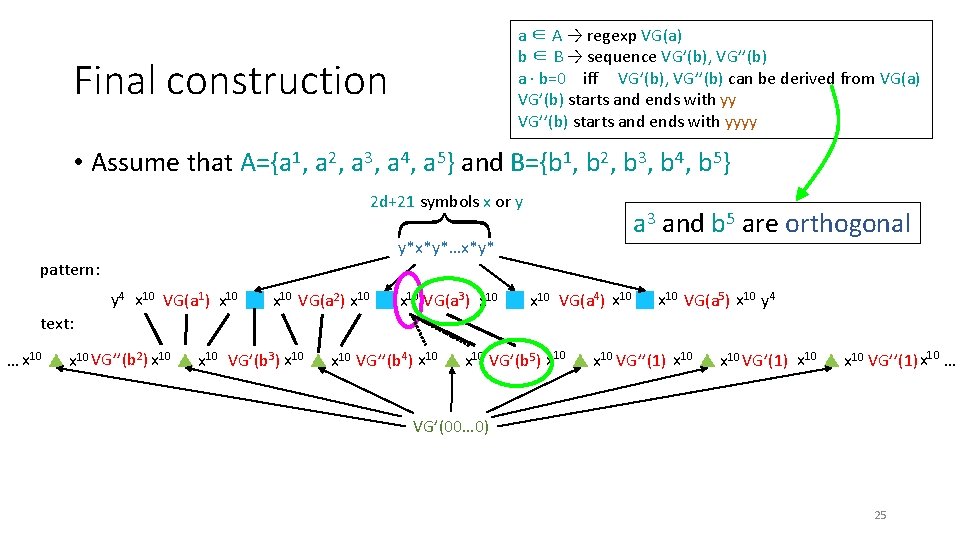
a ∈ A → regexp VG(a) b ∈ B → sequence VG’(b), VG’’(b) a · b=0 iff VG’(b), VG’’(b) can be derived from VG(a) VG’(b) starts and ends with yy VG’’(b) starts and ends with yyyy Final construction • Assume that A={a 1, a 2, a 3, a 4, a 5} and B={b 1, b 2, b 3, b 4, b 5} 2 d+21 symbols x or y { a 3 and b 5 are orthogonal y*x*y*…x*y* pattern: y 4 x 10 VG(a 1) x 10 VG(a 2) x 10 VG(a 3) x 10 VG(a 4) x 10 VG(a 5) x 10 y 4 text: … x 10 VG’’(b 2) x 10 VG’(b 3) x 10 VG’’(b 4) x 10 VG’(b 5) x 10 VG’’(1) x 10 … VG’(00… 0) 25

Conclusions • We classify regexp matching based on depth and type • We show dichotomy: regexp matching is either easy (near-linear time) or SETH-hard Thank you! 26