Where might I see inequalities in real life

Where might I see inequalities in real life?

� If it’s any smaller, you’ve got to throw him back!

12 -4 Inequalities An inequality states that two quantities either are not equal or may not be equal. An inequality uses one of the following symbols: Symbol < > Course 2 Meaning Word Phrases is less than Fewer than, below More than, above ≤ is greater than is less than or equal to ≥ is greater than or equal to At least, no less than At most, no more than

And: Symbol ≠ Meaning is not equal to Word Phrases Is not equal to

An inequality that contains a variable is an algebraic inequality. A value of the variable that makes the inequality true is a solution of the inequality. An inequality may have more than one solution. Together, all of the solutions are called the solution set.

Write an inequality for each situation. A. There at least 15 people in the waiting room. number of people ≥ 15 or x ≥ 15 “At least” means greater than or equal to. B. The tram attendant will allow no more than 60 people on the tram. “No more than” means number of people ≤ 60 or less than or equal to. x ≤ 60

12 -4 Inequalities Check It Out: Example 1 Write an inequality for each situation. C. There at most 10 gallons of gas in the tank. gallons of gas ≤ 10 or x ≤ 10 “At most” means less than or equal to. D. There at least 10 yards of fabric left. yards of fabric ≥ 10 or x ≥ 10 Course 2 “At least” means greater than or equal to.

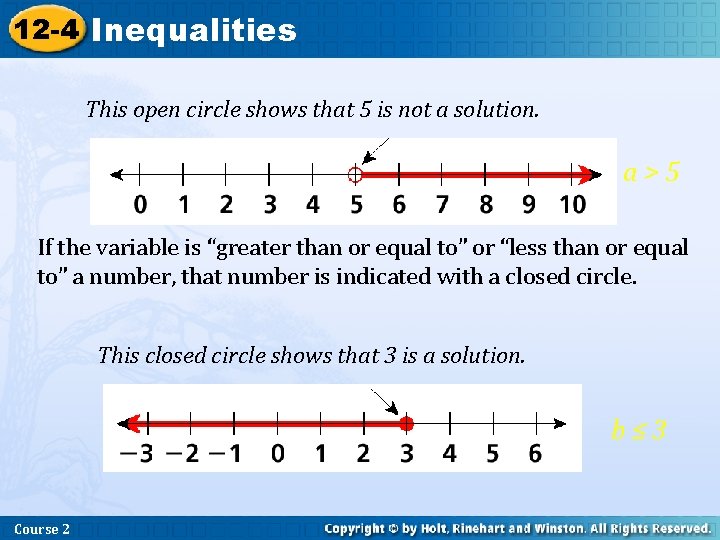
12 -4 Inequalities You can graph the solutions of an inequality on a number line. If the variable is “greater than” or “less than” a number, then that number is indicated with an open circle. To indicate that solutions include numbers with values less than the point graphed, shade to the left of the point. To show that solutions include numbers greater than the point graphed, shade to the right of the point. Course 2

12 -4 Inequalities This open circle shows that 5 is not a solution. a>5 If the variable is “greater than or equal to” or “less than or equal to” a number, that number is indicated with a closed circle. This closed circle shows that 3 is a solution. b≤ 3 Course 2

12 -4 Inequalities Additional Example 2: Graphing Simple Inequalities On your own paper, graph each inequality. A. n < 3 – 2 – 1 0 1 2 B. a ≥ – 4 – 6 – 4 Course 2 – 2 0 2 4 6 3 3 is not a solution, so draw an open circle at 3. Shade the line to the left of 3. – 4 is a solution, so draw a closed circle at – 4. Shade the line to the right of – 4.

12 -4 Inequalities Check It Out: Example 2 On your own paper, graph each inequality. A. p ≤ 2 – 3 – 2 – 1 0 1 2 3 B. e > – 2 – 3 – 2 – 1 Course 2 0 1 2 3 2 is a solution, so draw a closed circle at 2. Shade the line to the left of 2. – 2 is not a solution, so draw an open circle at – 2. Shade the line to the right of – 2.

12 -4 Inequalities Insert Lesson Title Here Lesson Quiz: Part II Graph the inequalities on your own paper. 1. x > – 1 º – 3 – 2 – 1 0 1 2 3 2. x < – 1 º – 3 – 2 – 1 Course 2

12 -4 Inequalities Insert Lesson Title Here Lesson Quiz: Part II Graph the inequalities, continued. 3. x > – 1 º – 3 – 2 – 1 0 1 2 3 4. x < – 1 º – 3 – 2 – 1 Course 2

Inequalities Solving inequalities