Where have we been Vector Concepts Describing Vectors

Where have we been? Vector Concepts Describing Vectors Comparing to Scalars Understanding acceleration Adding Displacements Adding Velocities

Forces Concepts Another kind of vector

Vocabulary

BY THE END OF THE LESSON, YOU WILL ……. 1. Describe the four basic types of forces. 2. Give examples of forces from everyday life. 3. What is the difference between a field force and a contact force? 4. Give examples from everyday life of field forces and contact forces. 5. Summarize Newton’s three laws of motion. 6. How are seat belts related to Newton’s laws of motion? 7. Identify the action-reaction forces when a tennis racket hits a tennis ball. 8. What are two variables that can be manipulated to change the acceleration of an object? 9. What is the relationship between an object’s mass and its inertia? 10. How can the force equation be rearranged to solve for either mass or acceleration? T O D A Y ‘S G O A L S

What is a force? A push or pull that is capable of changing the motion of an object.

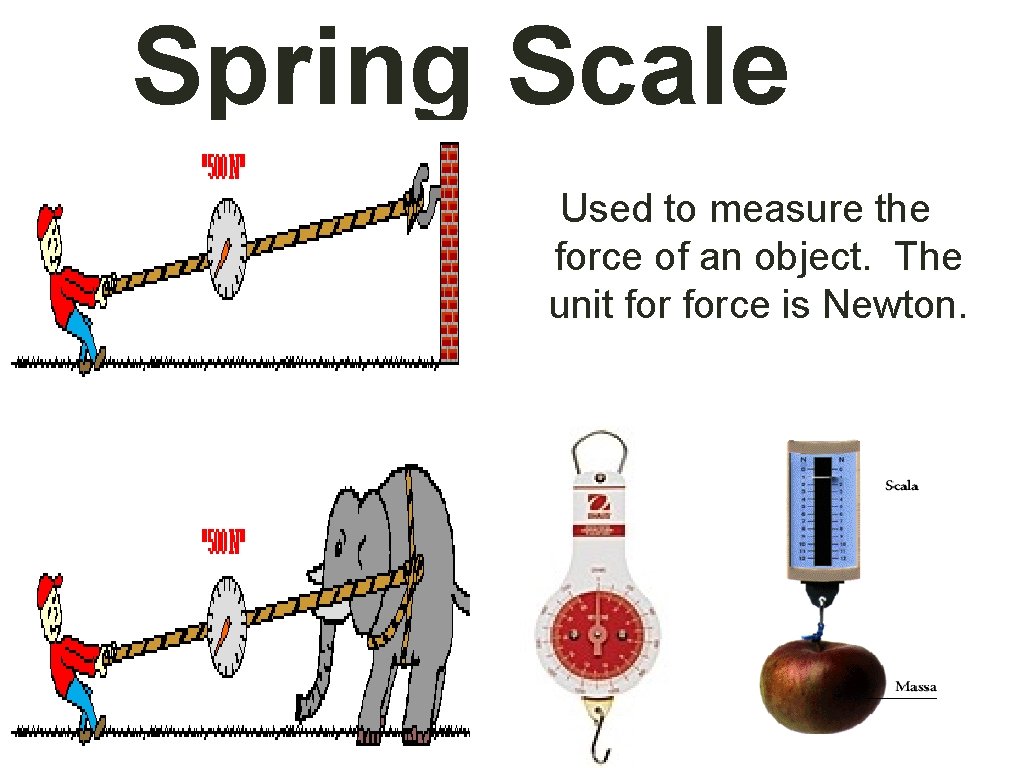
Spring Scale Used to measure the force of an object. The unit force is Newton.

Everyday Forces: • • • Tension Gravitational Force Friction Strong Nuclear Force Weight / Gravity Weak Nuclear Force Normal Force Air resistance Electrostatic Force

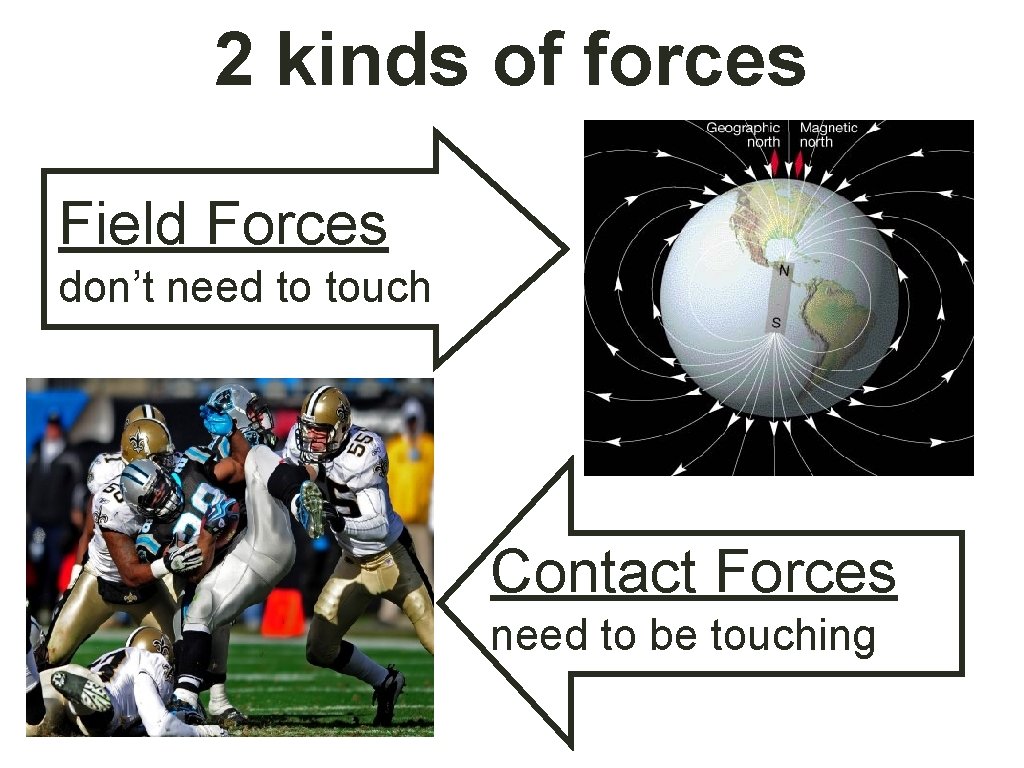
2 kinds of forces Field Forces don’t need to touch Contact Forces need to be touching

Normal Force FN • When in contact with a surface, the surface exerts a supporting force on the object. • This force is perpendicular to the surface and called the normal force. • If on a horizontal surface, Fnormal is equal in magnitude, but opposite in direction to Fgravity

Friction • Friction resists motion between touching surfaces. • Even smooth surfaces made of molecules that form little bumps, which cause resistance when they rub together. • So friction pushes in the opposite direction of the object’s motion. • Friction cause rolling objects to stop.

If forces push or pull to cause motion, why isn’t everything moving? • Forces can balance each other out. • When the forces are balanced on an object, the object is either not moving or has constant velocity.

Force Diagrams • The effect of a force depends on both magnitude and direction. Thus, force is a vector quantity. • Diagrams that show force vectors as arrows are called force diagrams. • Force diagrams that show only the forces acting on a single object are called freebody diagrams.

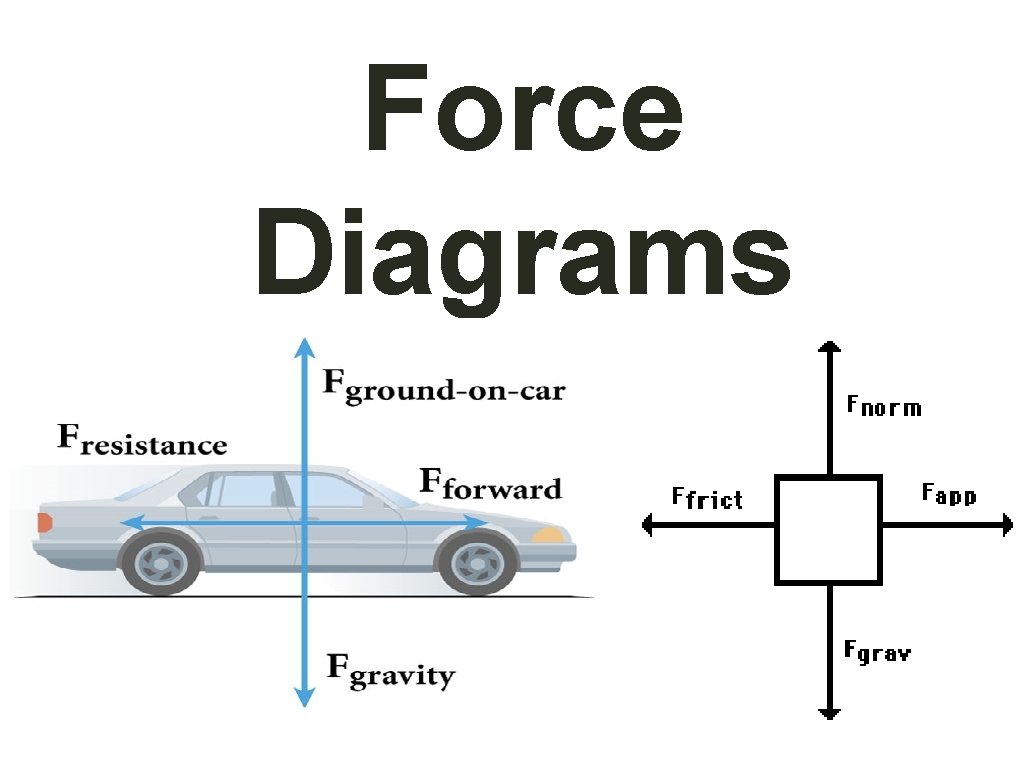
Force Diagrams

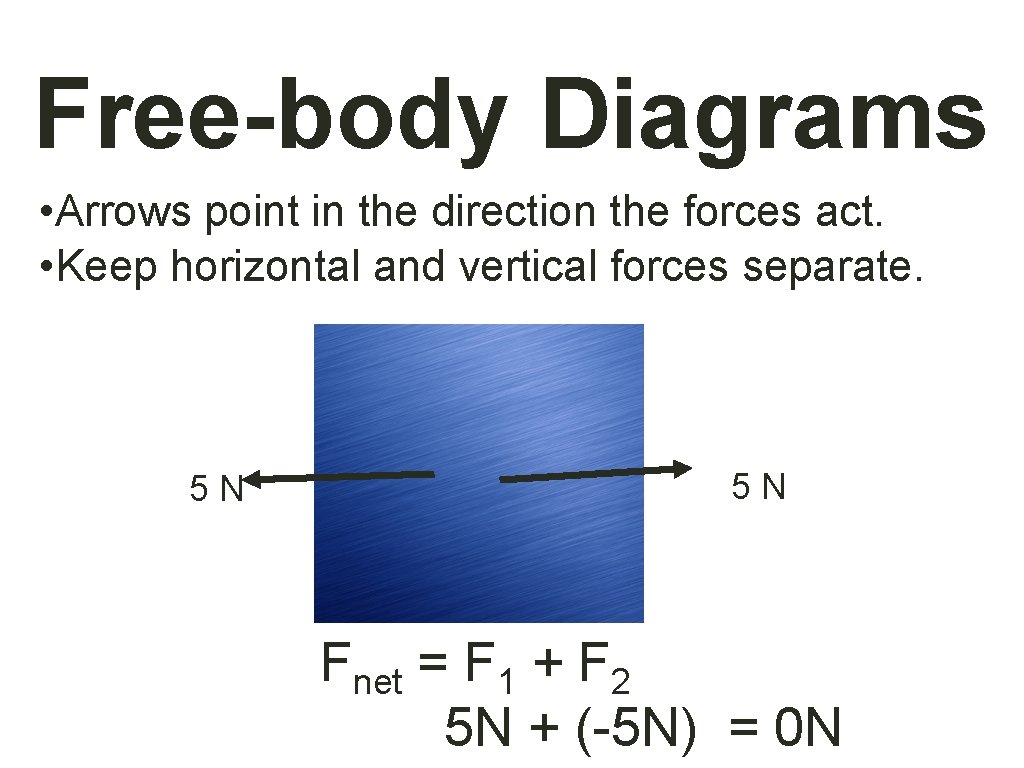
Free-body Diagrams • Arrows point in the direction the forces act. • Keep horizontal and vertical forces separate. 5 N Fnet = F 1 + F 2 5 N + (-5 N) = 0 N

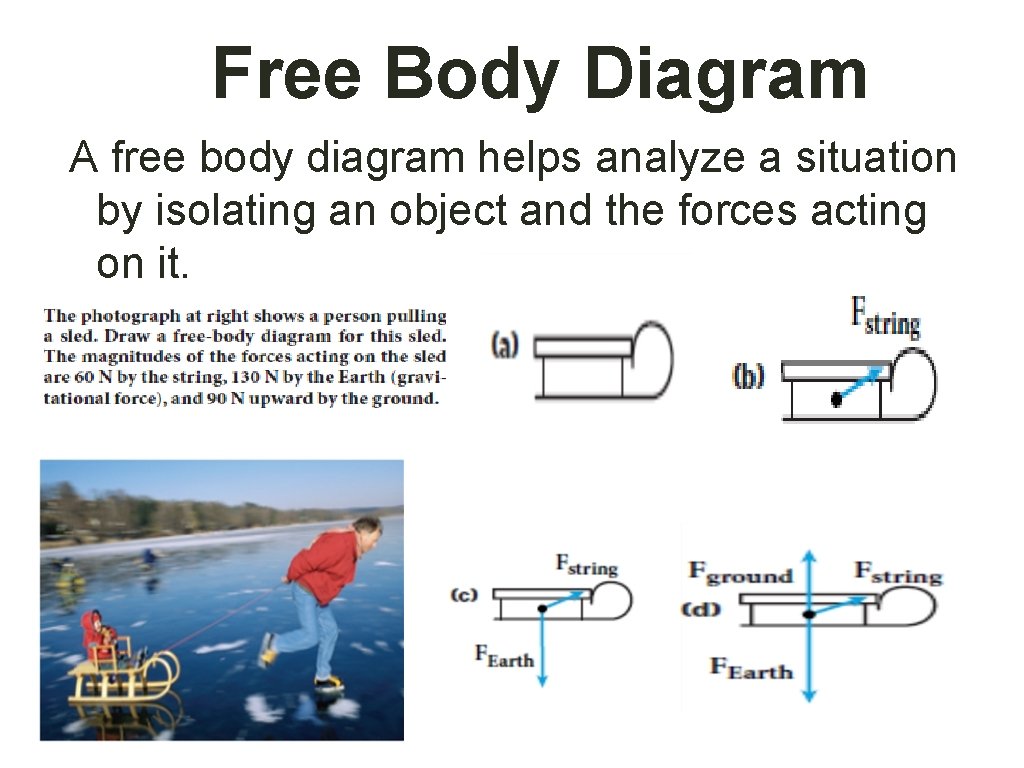
Free Body Diagram A free body diagram helps analyze a situation by isolating an object and the forces acting on it.

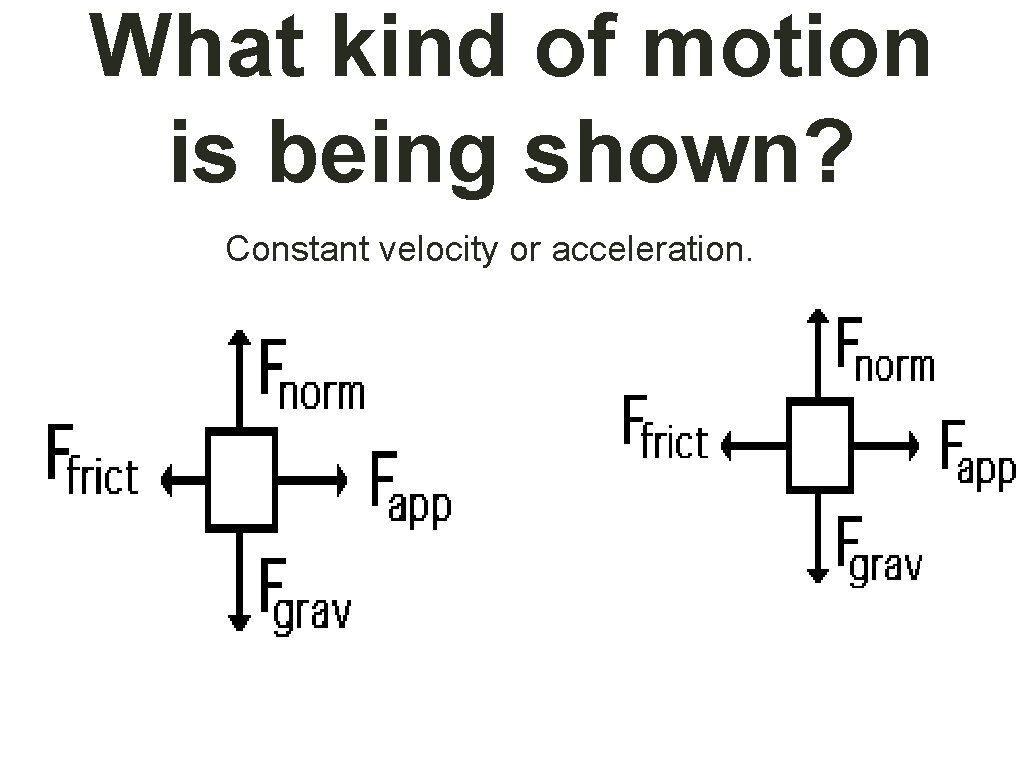
What kind of motion is being shown? Constant velocity or acceleration.

A physics book is at rest on a desk. Gravitational force pulls the book down. The desk exerts an upward force on the book that is equal in magnitude to the gravitational force. Draw a free-body diagram of the book.

Draw Free-body Diagram! 1. An egg is free-falling from a nest in a tree. Neglect air resistance. Diagram the forces acting on the egg as it is falling. 2. A force is applied to the right to drag a sled across loosely packed snow with a rightward acceleration. Diagram the forces acting upon the sled. 3. A flying squirrel is gliding (no wing flaps) from a tree to the ground at constant velocity. Consider air resistance. 4. An egg is free-falling from a nest in a tree. Include air resistance. Diagram the forces acting on the egg as it is falling. 5. A rightward force is applied to a book in order to move it across a desk at constant velocity. Consider frictional forces. Neglect air resistance.

Net Force • The sum of all forces acting on an object is called the resultant force or net force (Fnet). Fnet = F 1 + F 2 + F 3. . .

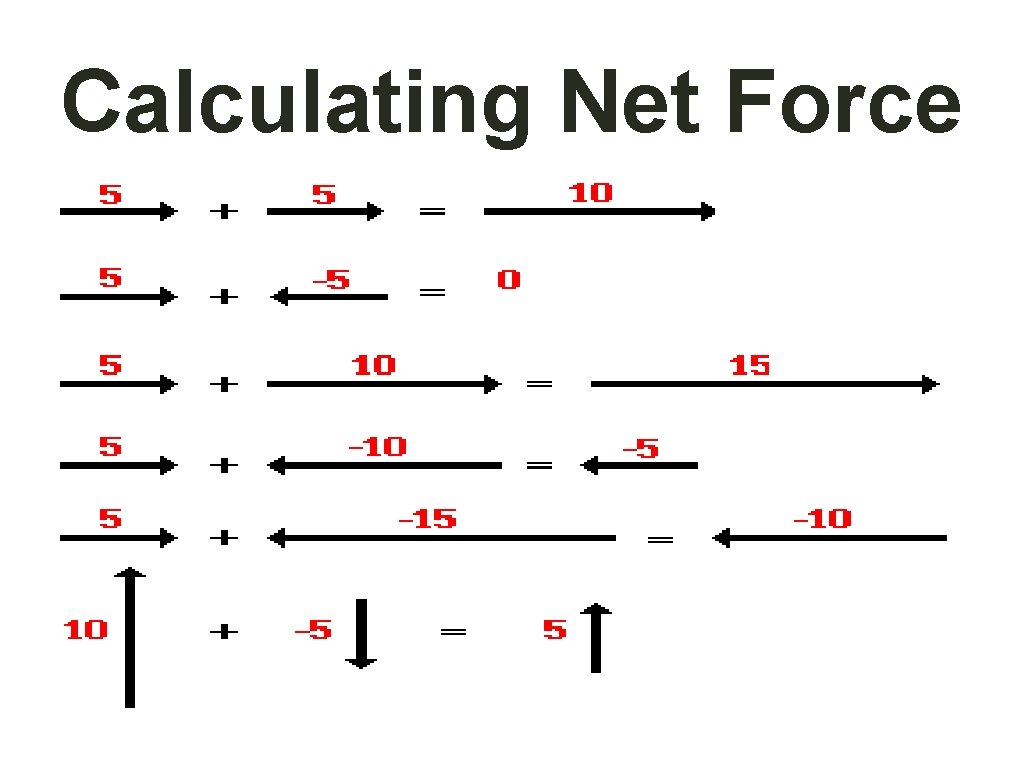
Calculating Net Force

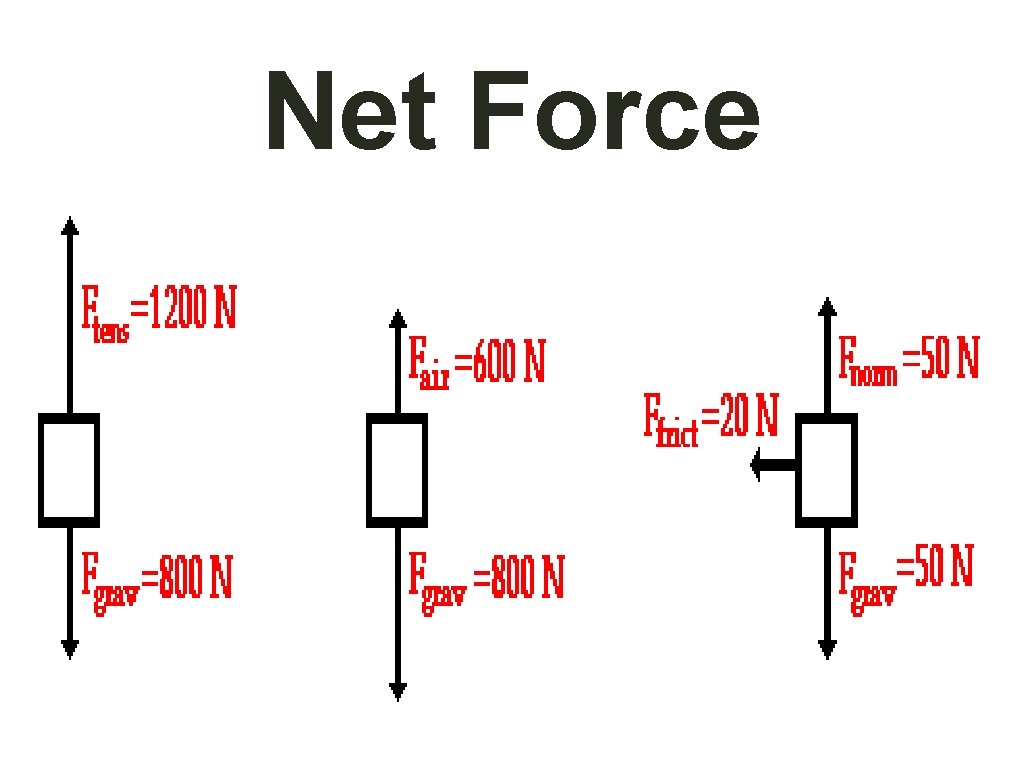
Net Force

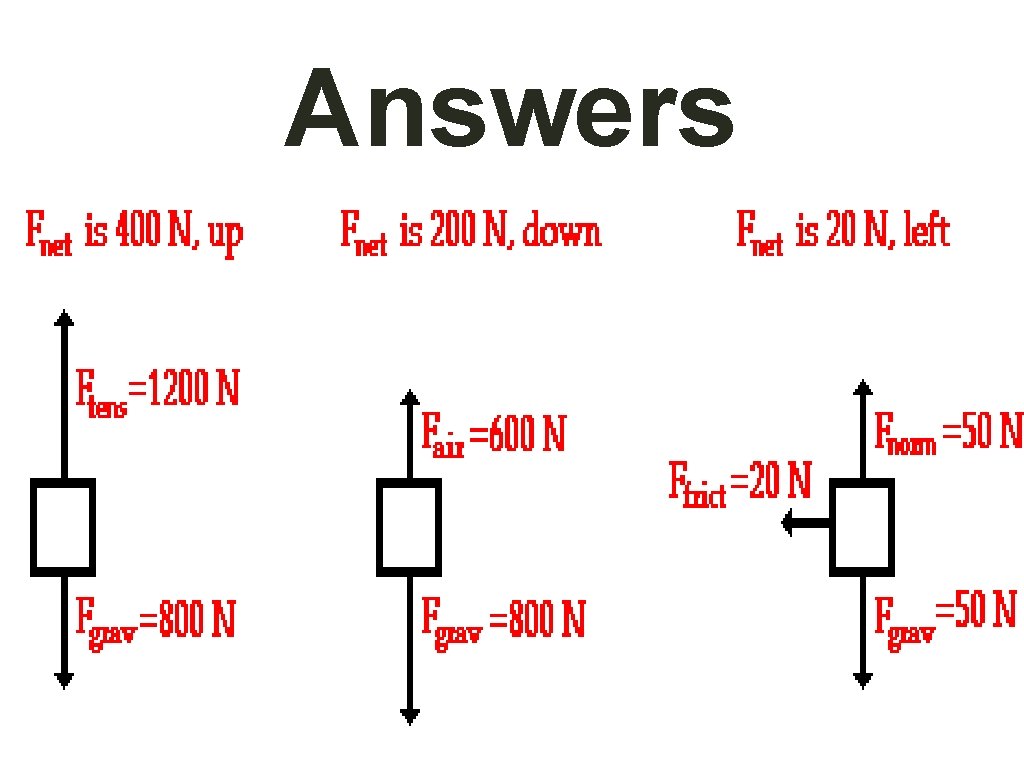
Answers

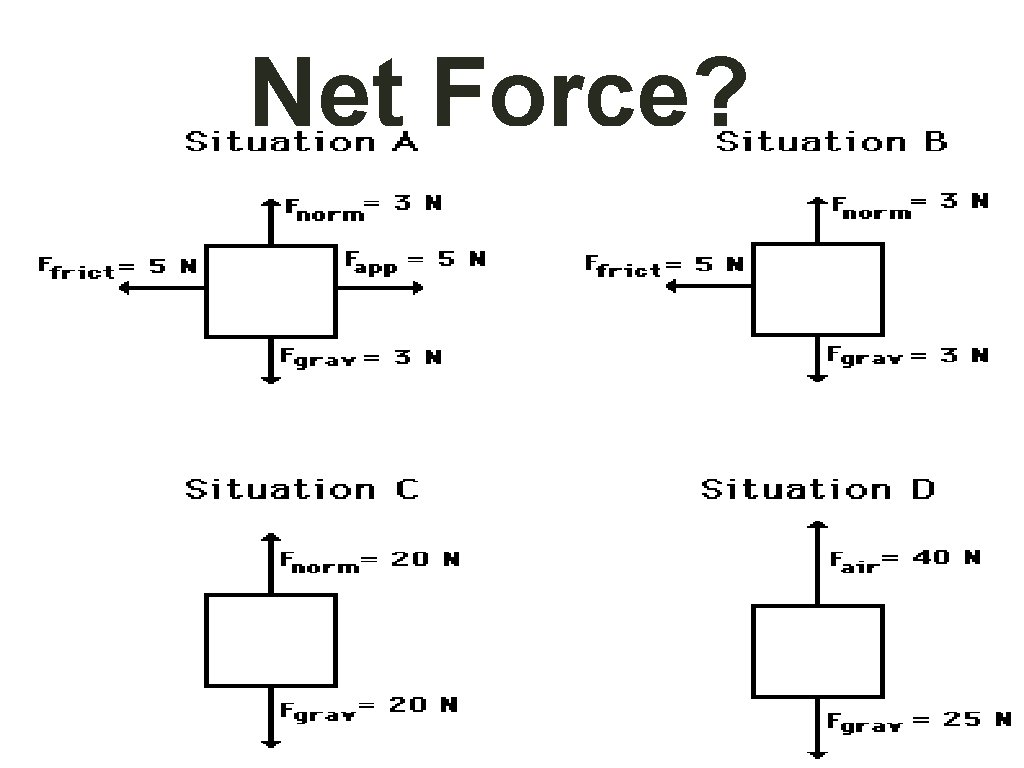
Net Force?

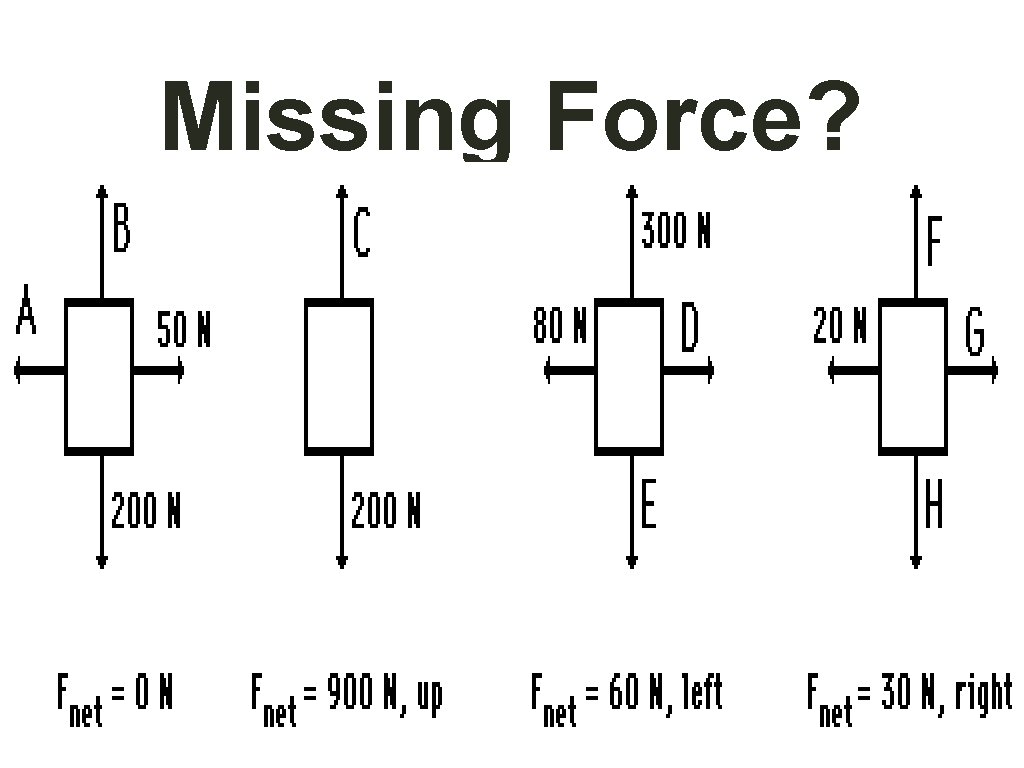
Missing Force?

Newton’s 3 Laws explain the relationship between forces and motion. He also watched apples fall to come up with universal gravitation.

Newton’s 1 st Law. • Objects in motion stay in motion • Objects at rest stay at rest *Unless acted upon by an unbalanced force. • The more mass, the more inertia. A. K. A. The law of Inertia

Newton’s st 1 law

Newton’s st 1 Law

Newton’s 2 nd Law. • Force = mass x acceleration • Bigger masses need bigger forces for equal acceleration • Bigger forces cause greater acceleration

Newton’s nd 2 law

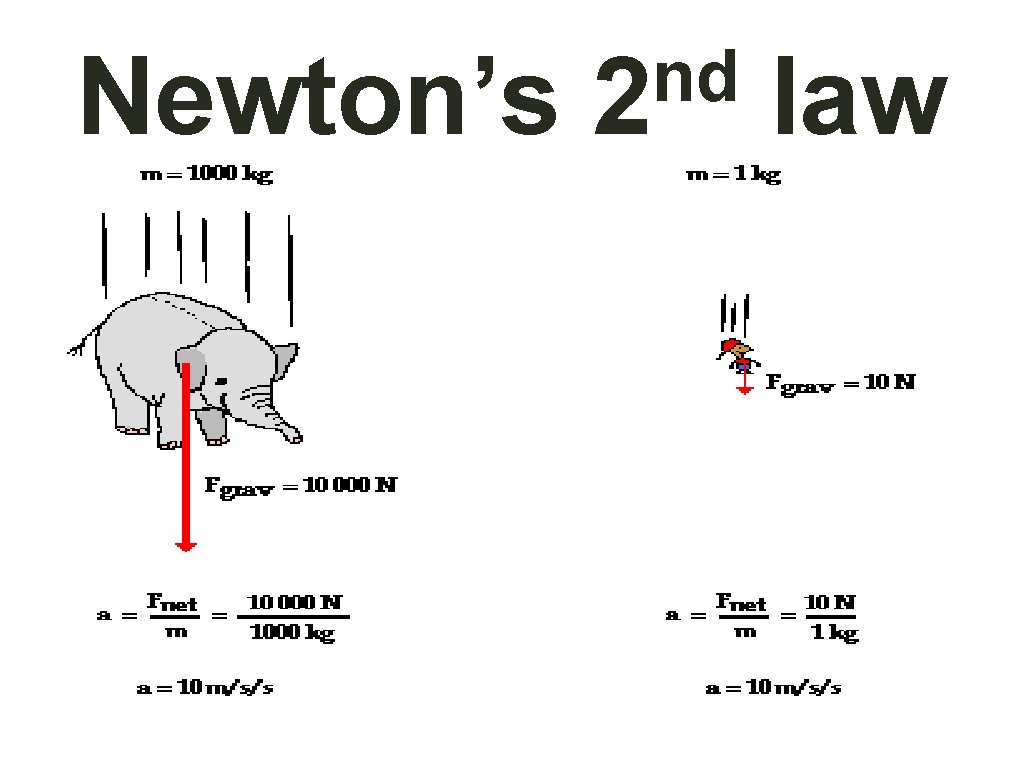
Newton’s nd 2 law

Newton’s nd 2 Law

Newton’s 3 rd Law. • For every force there is an equal and opposite force. • Both forces happen at the same time!

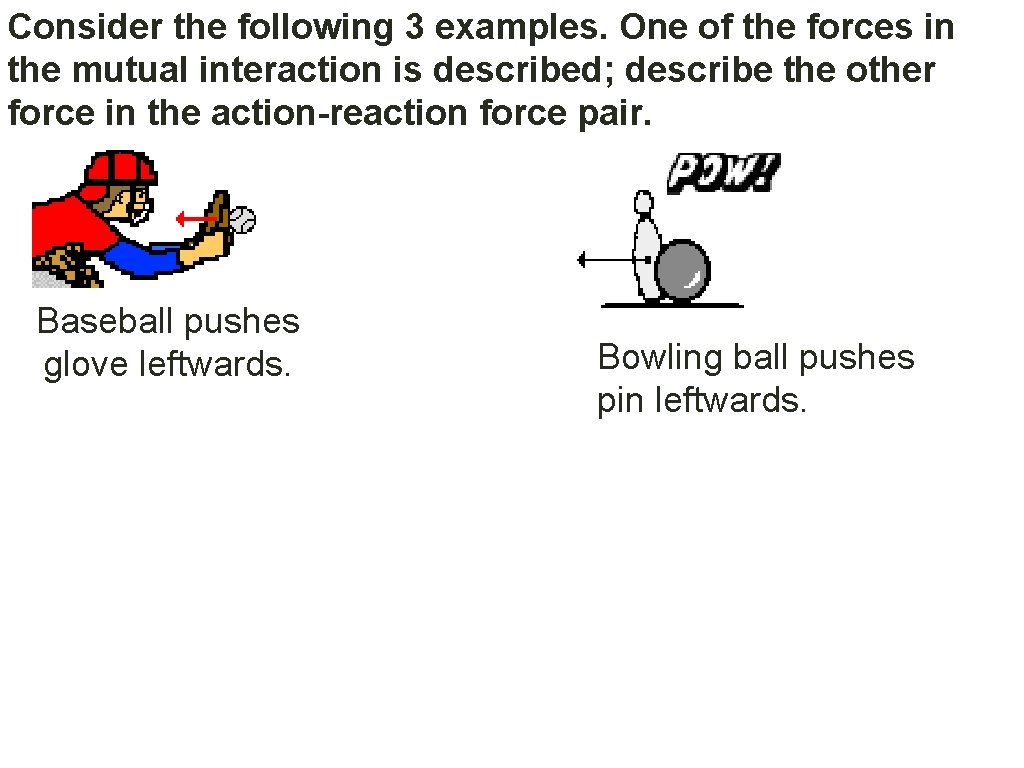
Consider the following 3 examples. One of the forces in the mutual interaction is described; describe the other force in the action-reaction force pair. Baseball pushes glove leftwards. Bowling ball pushes pin leftwards.

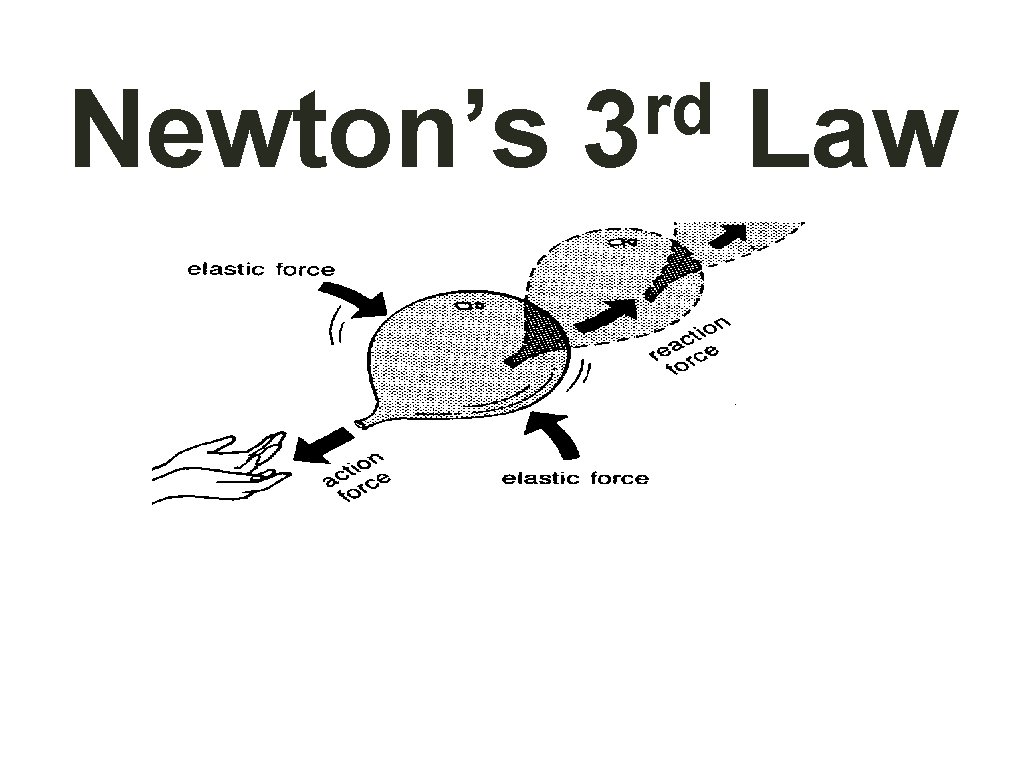
Newton’s rd 3 Law

Law of universal gravitation: • The force of gravity depends on mass and distance. • The greater the mass, the greater the force of gravity • The least distance will have a stronger gravitational force. Observe how the force of gravity is directly proportional to the product of the two masses and inversely proportional to the square of the distance of separation.

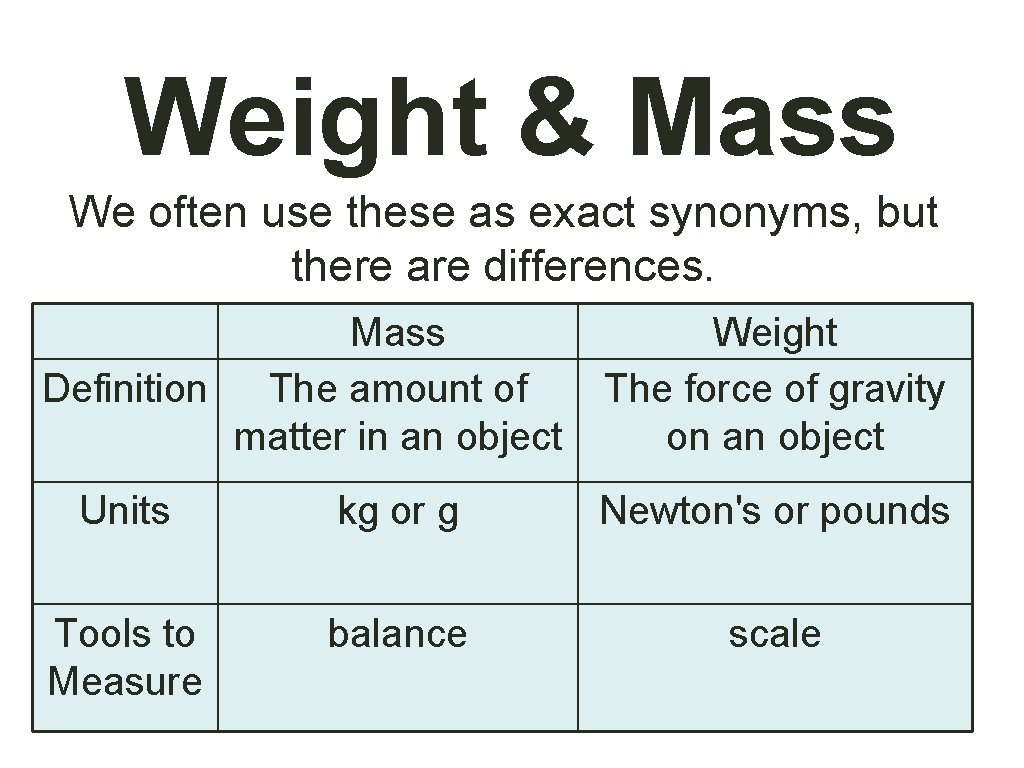
Weight & Mass We often use these as exact synonyms, but there are differences. Mass Definition The amount of matter in an object Weight The force of gravity on an object Units kg or g Newton's or pounds Tools to Measure balance scale

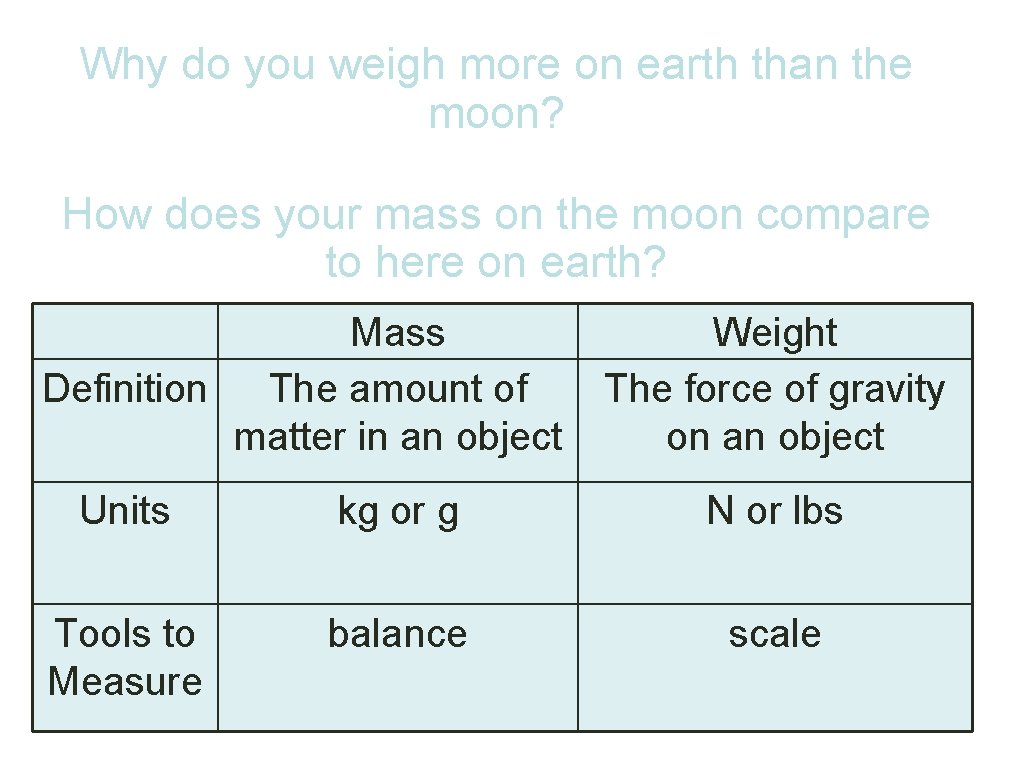
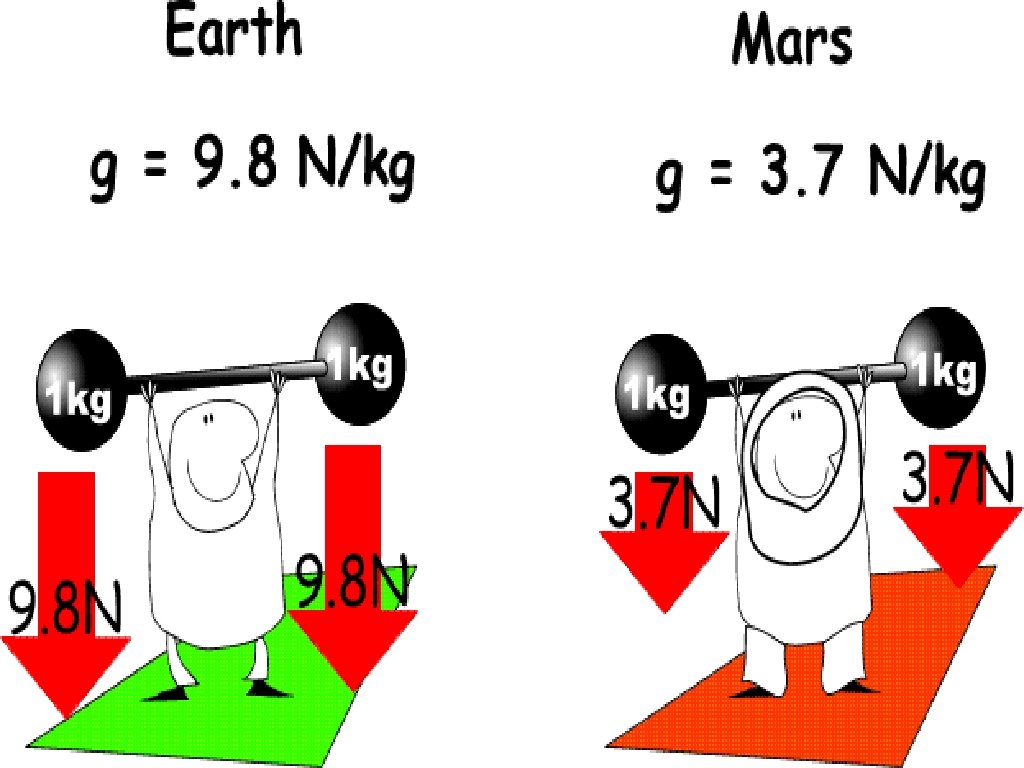
Why do you weigh more on earth than the moon? How does your mass on the moon compare to here on earth? Mass Definition The amount of matter in an object Weight The force of gravity on an object Units kg or g N or lbs Tools to Measure balance scale

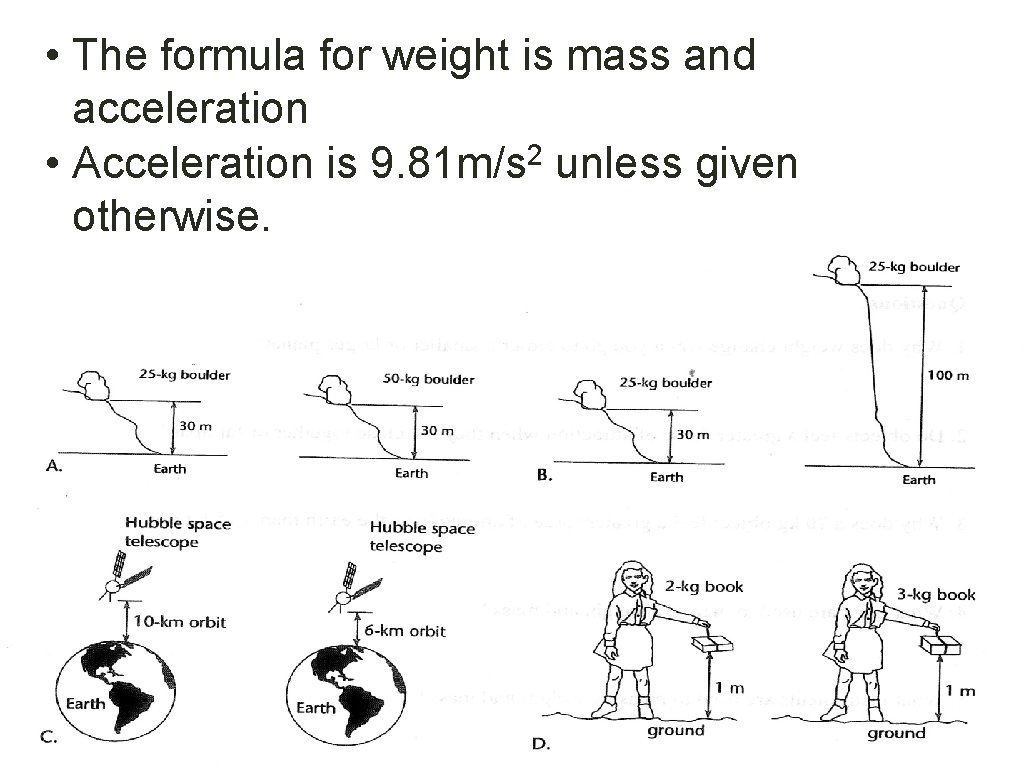
• The formula for weight is mass and acceleration • Acceleration is 9. 81 m/s 2 unless given otherwise.

W(Fg) = ma • A bag of sugar has a mass of 2. 26 kg. What is its weight on Earth? What is its weight on the moon, where the 2 gravitational constant is 1. 64 m/s ? What is its weight on Jupiter, where its gravitational constant is 25. 9 m/s 2? .

Concept Question Will a dart shot from a dart gun go farther horizontally on Earth or on the moon? Disregard air resistance. The dart will travel farther on the moon. Because the dart is accelerated downward more slowly on the moon than on Earth, it is in motion for a longer time on the moon. The horizontal velocity will be the same in each case.

Force abbreviations 1. Fg – gravitational force (can also be weight) 2. Fn – normal force (opposes gravity on surfaces-supporting force) 3. Fa – applied force (can be in any direction; can be more than one) 4. Ff – frictional force (air resistance is a frictional force)

Important Notes 1. To find net force, you would use Newton’s law of motion if mass and acceleration can be determined. 2. When you are given opposing forces, you would find net force by subtracting. 3. Weight = mass x 9. 8 m/s 2 (can also be used as Fg); Weight is a force; 9. 8 m/s 2 is used as the acceleration unless the problem states that you are not on Earth

Example 1. On planet X, a 50 -kg barbell can be lifted by exerting a force of 180 N. A) What is the acceleration due to gravity on planet X? b) What minimum force is required to lift the same barbell on the earth? 2. An elevator that weigh 3. 0 x 103 N is accelerated upward at 2. 0 m/s 2. What force does the cable exert on the car to give it this acceleration?

Example An upward force of 148 N is applied to a 10 kg rock. 1. What is the force of gravity acting on the rock? 2. What is the net force acting on the rock? 3. What is the net acceleration of the rock?

Example 1) What is the force of friction when an applied force of 20 N accelerates a 5 kg rock at 3 m/s 2? 2 2) A 15 kg bike accelerates at 0. 5 m/s when an applied force of 10 N is exerted on it. How much friction is acting on it?

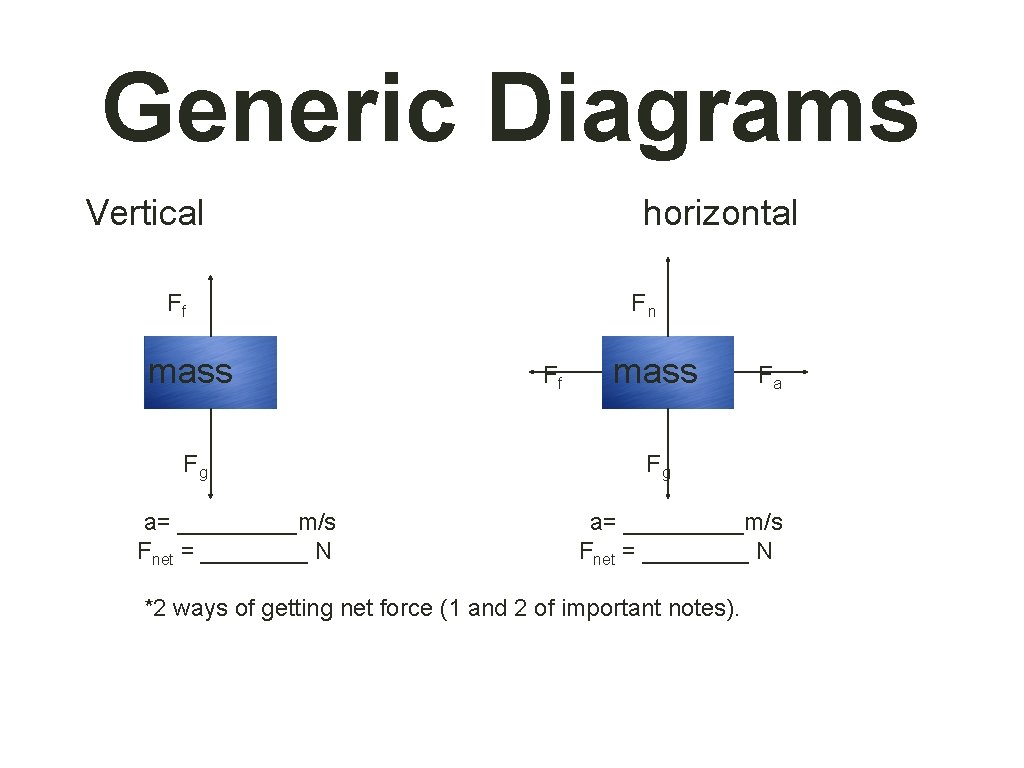
Generic Diagrams Vertical horizontal Ff F n mass Ff mass Fa Fg F g a= _____m/s Fnet = ____ N Fnet = ____ N *2 ways of getting net force (1 and 2 of important notes).

Example 1) A force of 40 N accelerates a 5 kg block at 1 m/s 2 along a horizontal surface. A) What is the net force acting on the block? B) What is the frictional force? 2) A 10 N box has an upward force of 15 N applied to it. Is the box accelerating? If so, what is its acceleration?

Friction The force of friction is always greater to start an object moving – this is called static friction.

Friction 3 kinds of friction: • Static: The force of friction is always greater when the object is not moving • Rolling/sliding: Frictional force when an object is moving is less than static. • Fluid friction: Air resistance is friction in air. • Objects with large surface area will experience great air resistance.

Ff is proportional to Fn • The coefficient of friction (represented by the letter µ) is a ratio of the frictional force acting on an object divided by the normal force acting on the object. Objects normally have a different coefficient of static friction (to get the object moving) from their coefficient of kinetic friction (to keep it moving once it has already starting moving. )

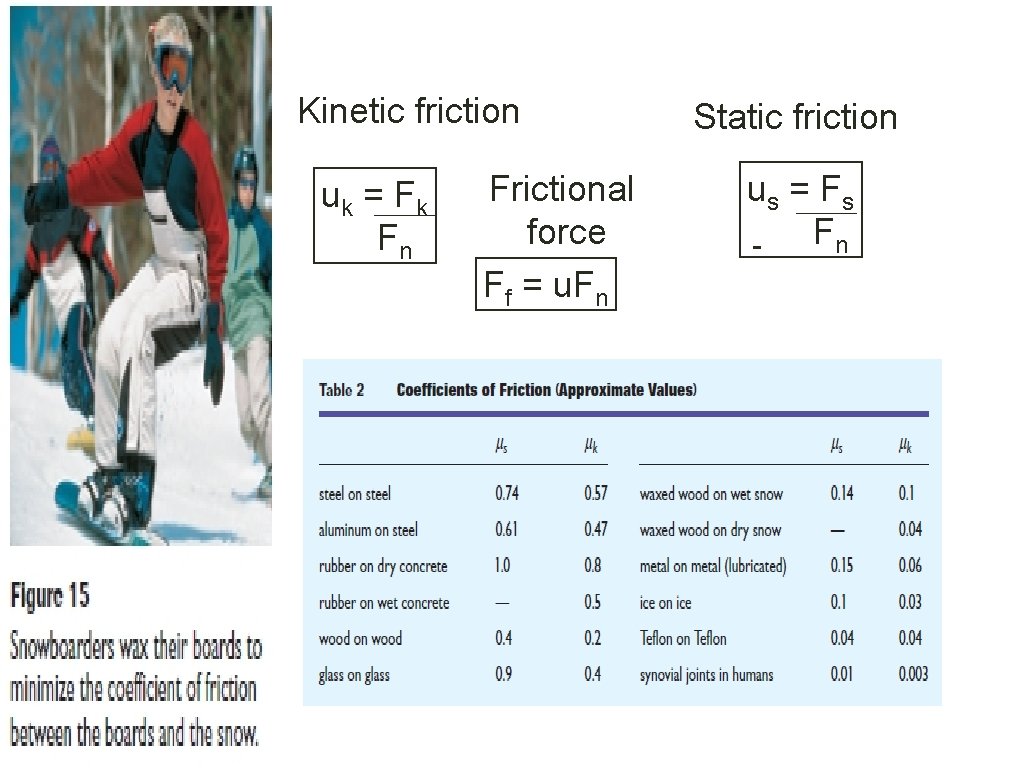
Kinetic friction uk = Fk Fn Frictional force Ff = u. Fn Static friction us = Fs Fn

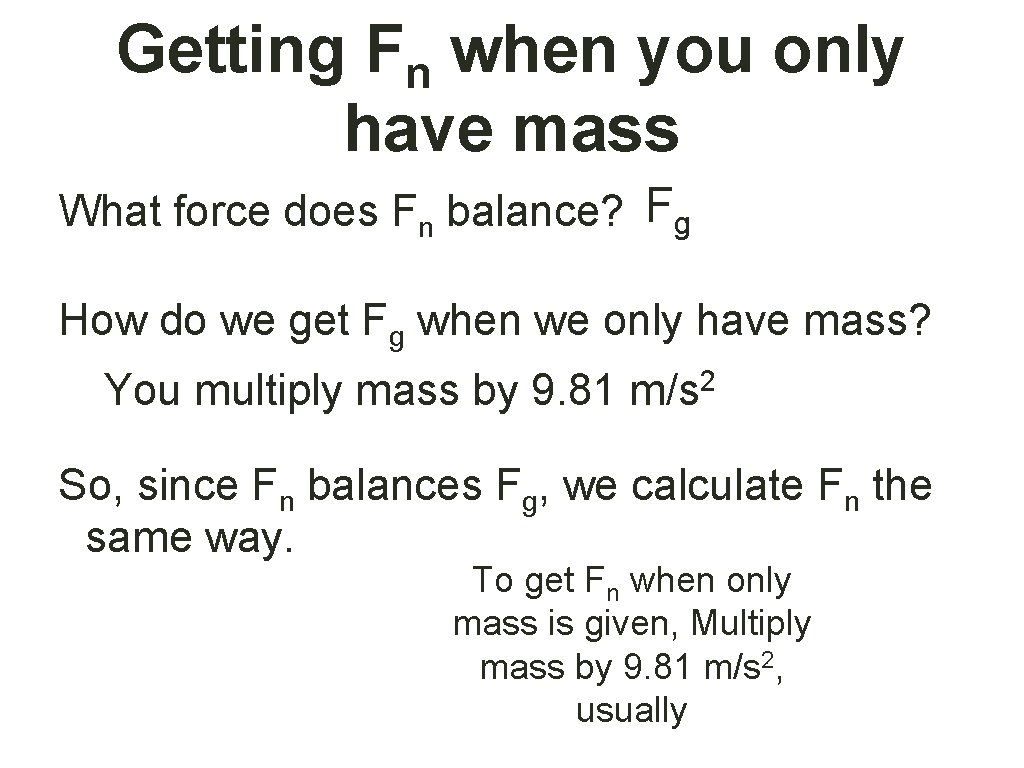
Getting Fn when you only have mass What force does Fn balance? Fg How do we get Fg when we only have mass? 2 You multiply mass by 9. 81 m/s So, since Fn balances Fg, we calculate Fn the same way. To get Fn when only mass is given, Multiply mass by 9. 81 m/s 2, usually

A 55 kg ice skater is at rest on a flat skating rink. A 198 N horizontal force is needed to set the skater in motion. However, after the skater is in motion, a horizontal force of 175 N keeps the skater moving at a constant velocity. Find the coefficients of static and kinetic friction between the skates and the ice.

A 24 kg crate initially at rest on a horizontal floor requires a 75 N horizontal force to set it in motion. Find the coefficient of static friction between the crate and the floor.

Forces KWL 1. Who is credited with “discovering” gravity? 2. Define inertia. 3. What is friction and how does it affect motion? 4. How is gravity important in space? 5. Describe how a plane’s wings help it fly. 6. What are two forces that affect those who go on amusement park rides such as roller coasters and rides that spin?

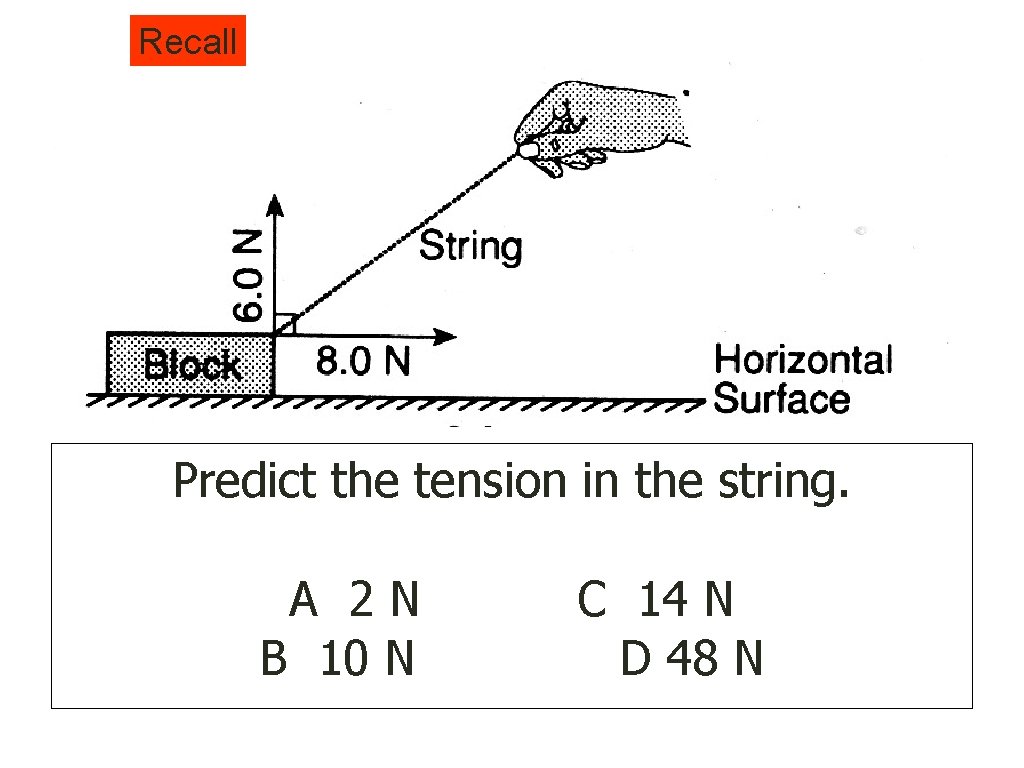
Recall Predict the tension in the string. A 2 N B 10 N C 14 N D 48 N

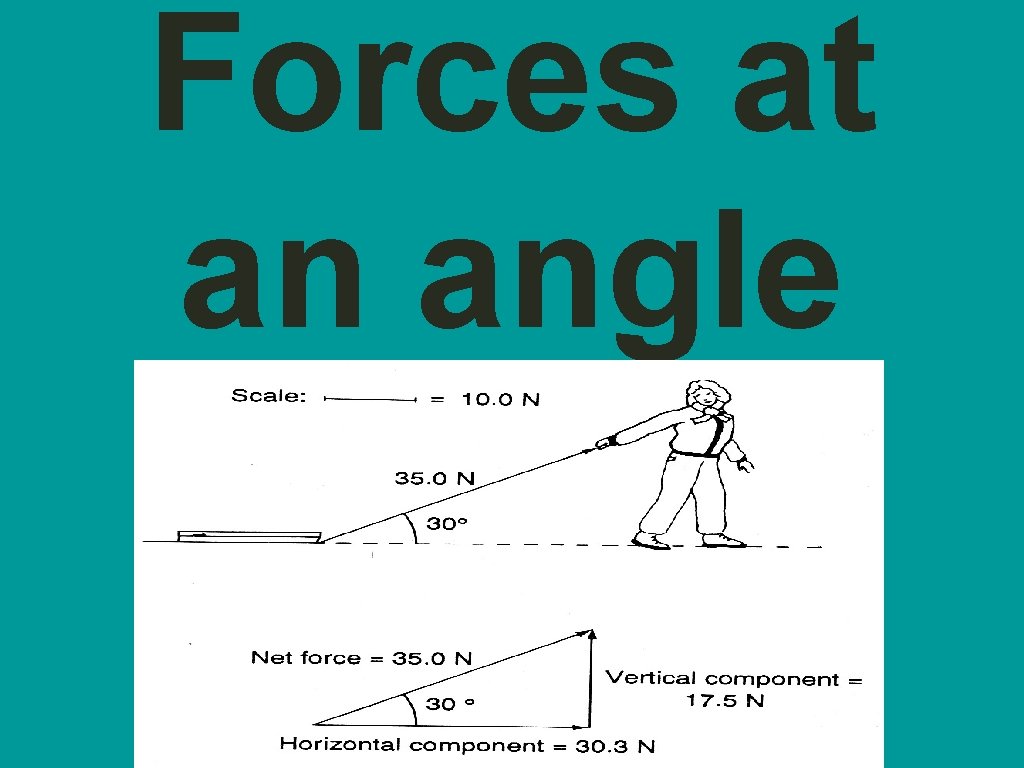
Forces at an angle

• When working with angles we need to separate x and y components sinθ = (o/h) cosθ = (a/h) tanθ = (o/a) • Fg = Weight = mg • Objects in equilibrium have balanced forces (Fnet = 0 N) Remember this?

Fa force responsible forward motion Fx • The applied force will be the force in the handle, which is usually represented as the hypotenuse. • The force responsible for the forward motion will be the horizontal component of the force. If the object moves at constant velocity, the horizontal component of the applied force is equal to the frictional force.

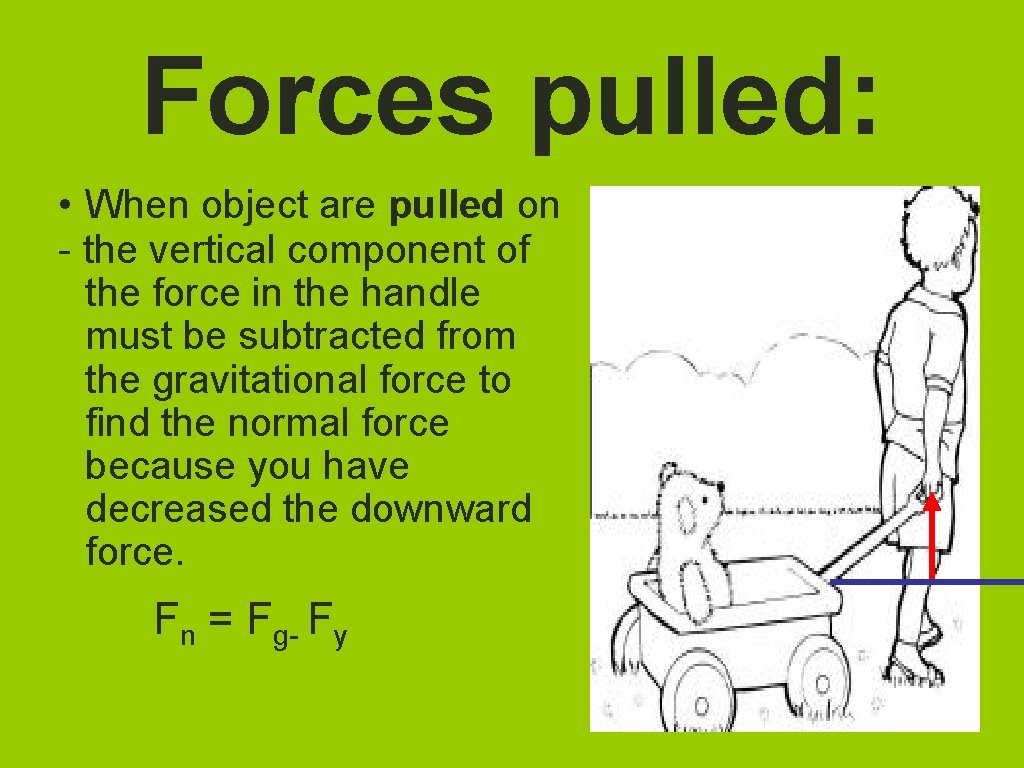
Forces pulled: • When object are pulled on - the vertical component of the force in the handle must be subtracted from the gravitational force to find the normal force because you have decreased the downward force. Fn = Fg- Fy

Forces pushed: When object are pushed on - the vertical component of the force in the handle must be added to the gravitational force to find the normal force because you have increased the downward force. Fn = Fy + Fg

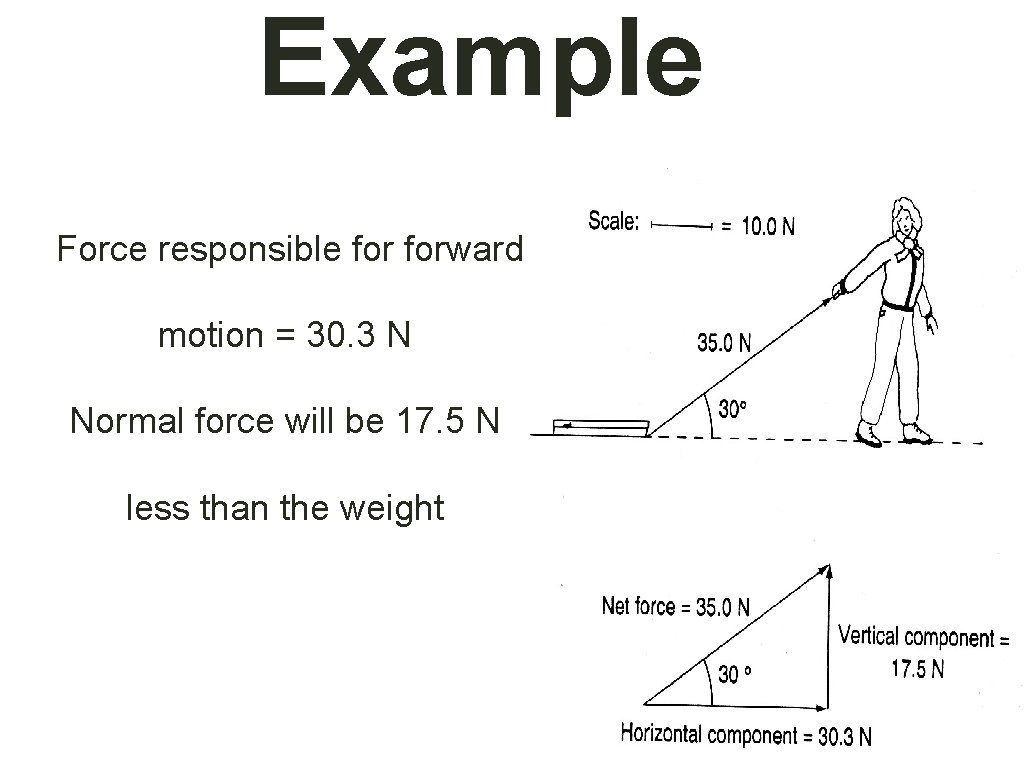
Example Force responsible forward motion = 30. 3 N Normal force will be 17. 5 N less than the weight

Ph. ET simulation: Click here

In equation form: m m 1 2 = F G 2 d F is the force of attraction, measured in NEWTONS, between masses m 1 and m 2 G is the Universal Gravitation Constant, equal to 6. 67 x 10 -11 N m 2/kg 2 m 1 and m 2 are the attracting masses, measured in KILOGRAMS d is the distance between their centers of mass, and is measured in METERS

In order to solve problems related to the law of universal kilogram gravitation, masses must be in the unit ______, meter and distance must be in the unit _________. As the mass of either of the objects increases, the gravitational force between the two objects increases ____________________. As the distance between the two objects increases, the gravitational force between the two objects decreases ___________________. Inverse The law is an example of an ___________ proportionate relationship ___________ because as the distance between the objects increases, the force of attraction between them decreases.

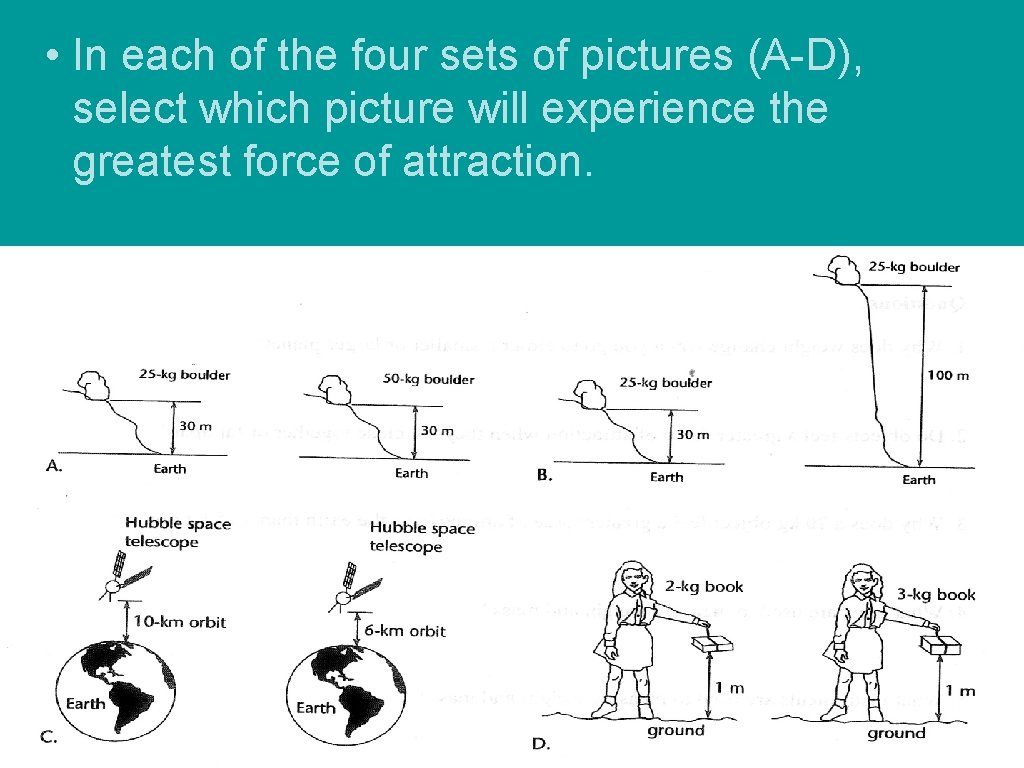
• In each of the four sets of pictures (A-D), select which picture will experience the greatest force of attraction.

Practice 1) What is the force of attraction between a 60. 0 kg boy and a 2 kg rock if they are 15 meters apart? 2) What force of attraction do the boy and the rock experience if their distance decreases three times? 3) Two balls are separated by 0. 250 km. What is their force of attraction if both balls have a mass of 1. 0 kg?

Circular Motion How things move as they spin

Foundations: remember this? • Speed is scalar (without direction), but velocity is a vector (direction counts) • acceleration is a changing velocity over time • So, could you have something moving at a constant speed, but still accelerating? How? • Newton’s Laws

In summary Uniform circular motion. . . • has constant speed • has changing direction for velocity • is caused by an inward “centripetal force” • experiences inward acceleration

Centripetal Force 2 v m Fc = –––– r 2 mass x velocity centripetal = –––––– force radius .

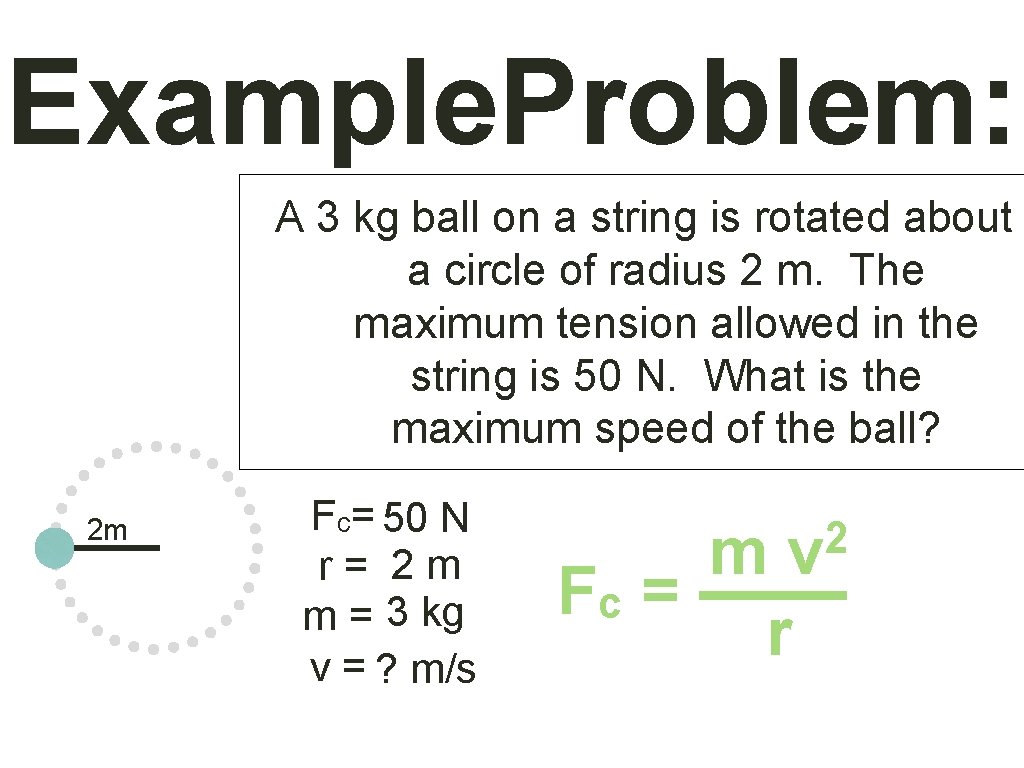
Example. Problem: A 3 kg ball on a string is rotated about a circle of radius 2 m. The maximum tension allowed in the string is 50 N. What is the maximum speed of the ball? 2 m Fc= 50 N r = 2 m m = 3 kg v = ? m/s 2 v m Fc = –––– r

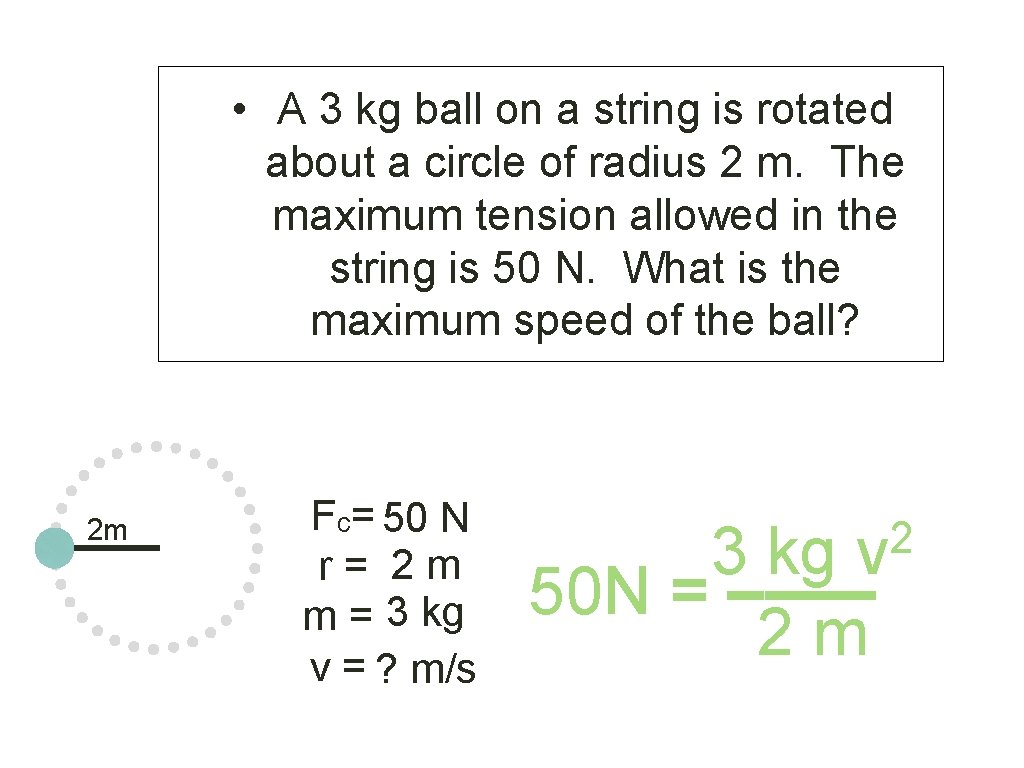
• A 3 kg ball on a string is rotated about a circle of radius 2 m. The maximum tension allowed in the string is 50 N. What is the maximum speed of the ball? 2 m Fc= 50 N r = 2 m m = 3 kg v = ? m/s 2 3 kg v 50 N = –––– 2 m

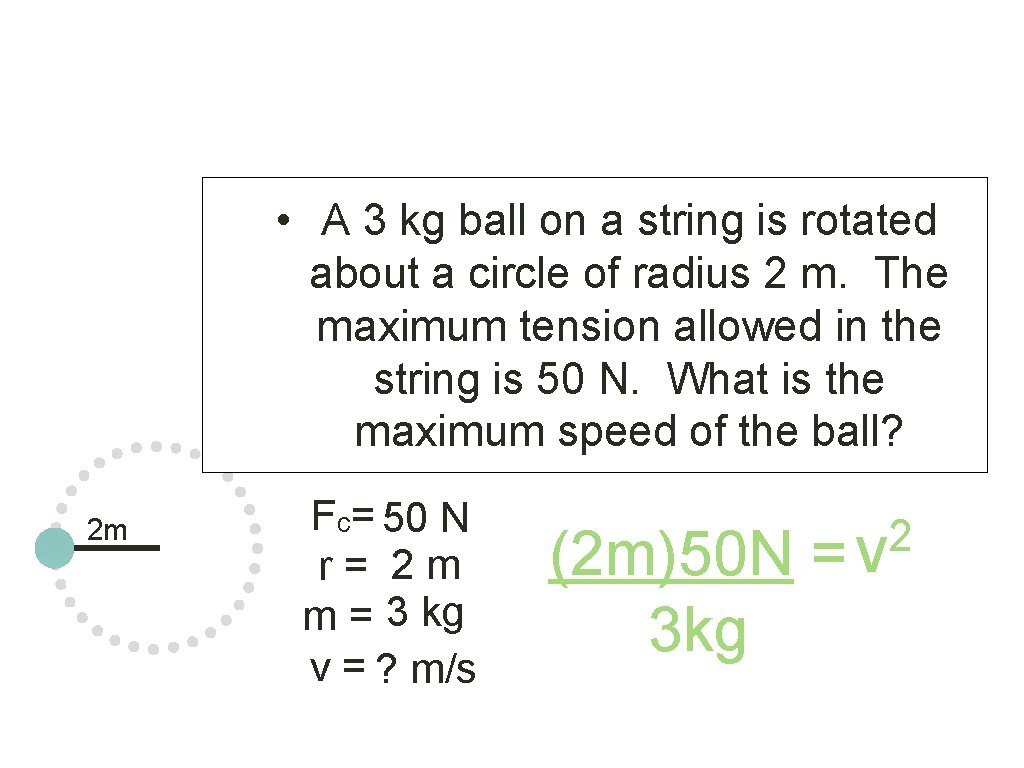
Example Problem: • A 3 kg ball on a string is rotated about a circle of radius 2 m. The maximum tension allowed in the string is 50 N. What is the maximum speed of the ball? 2 m Fc= 50 N r = 2 m m = 3 kg v = ? m/s (2 m)50 N = 3 kg 2 v

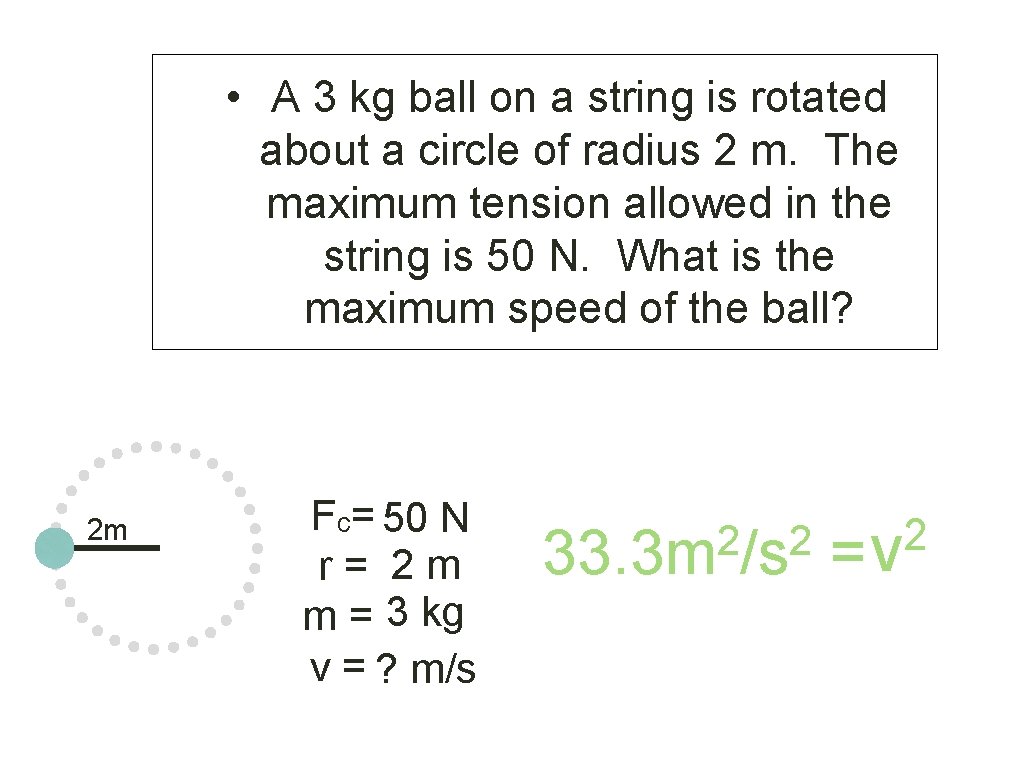
• A 3 kg ball on a string is rotated about a circle of radius 2 m. The maximum tension allowed in the string is 50 N. What is the maximum speed of the ball? 2 m Fc= 50 N r = 2 m m = 3 kg v = ? m/s v 2 2 2 33. 3 m /s =

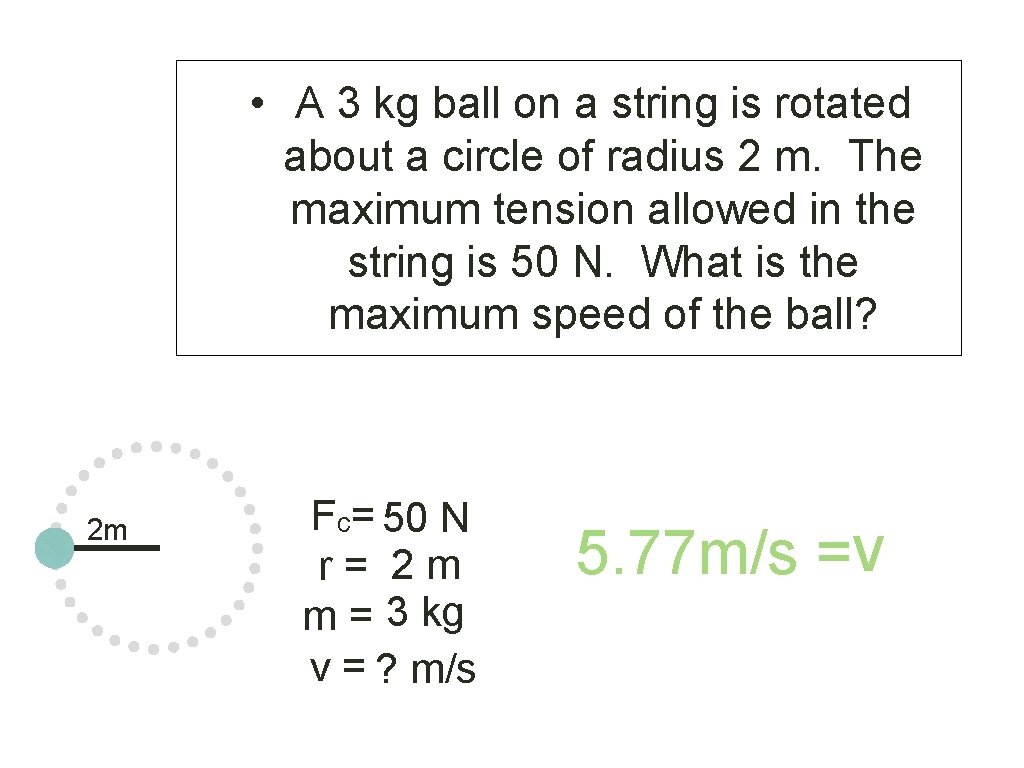
• A 3 kg ball on a string is rotated about a circle of radius 2 m. The maximum tension allowed in the string is 50 N. What is the maximum speed of the ball? 2 m Fc= 50 N r = 2 m m = 3 kg v = ? m/s 5. 77 m/s =v

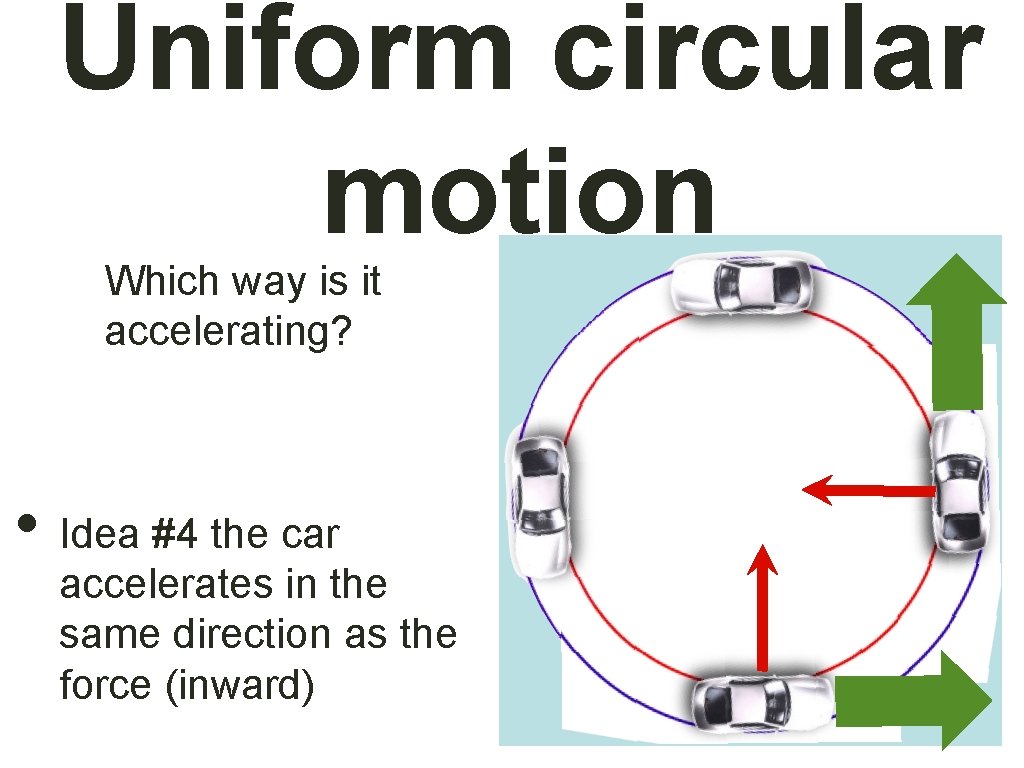
Uniform circular motion Which way is it accelerating? • Idea #4 the car accelerates in the same direction as the force (inward)

• A 2 kg ball on a string is rotated about a circle of radius 10 m. The maximum tension allowed in the string is 50 N. – What is the direction of the force needed to keep the ball moving in the circular path? – What is the maximum speed of the ball?

• During the course of a turn, an automobile doubles its speed. – How much additional frictional force must the tires provide if the car safely makes around the curve?

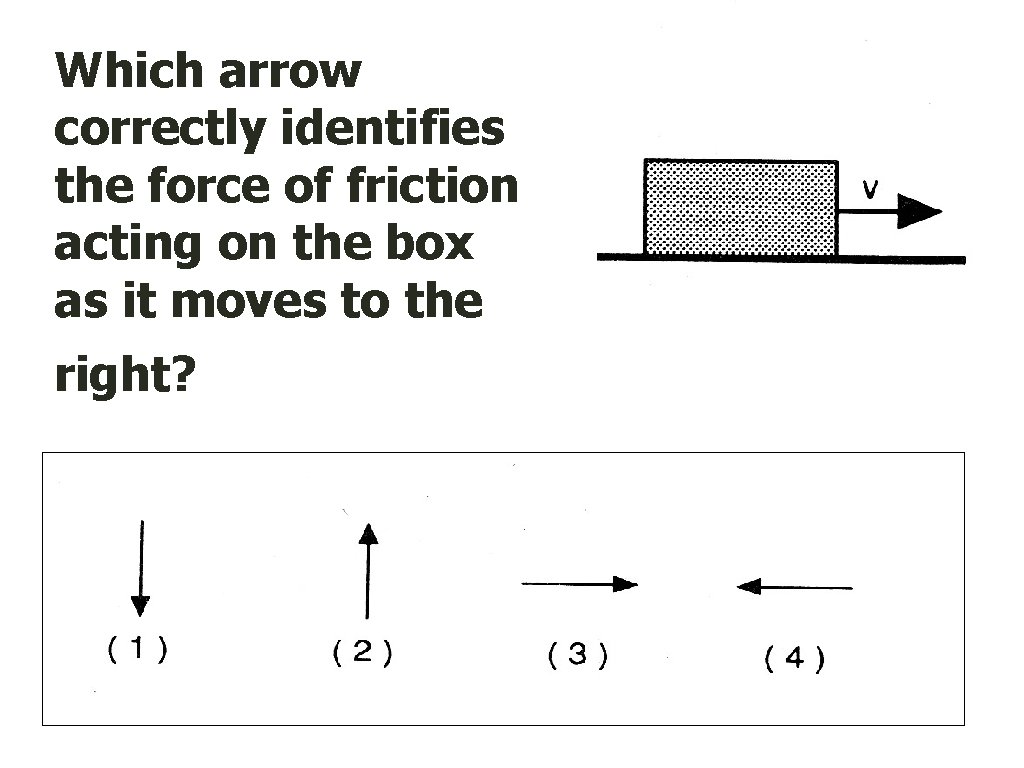
Which arrow correctly identifies the force of friction acting on the box as it moves to the right?

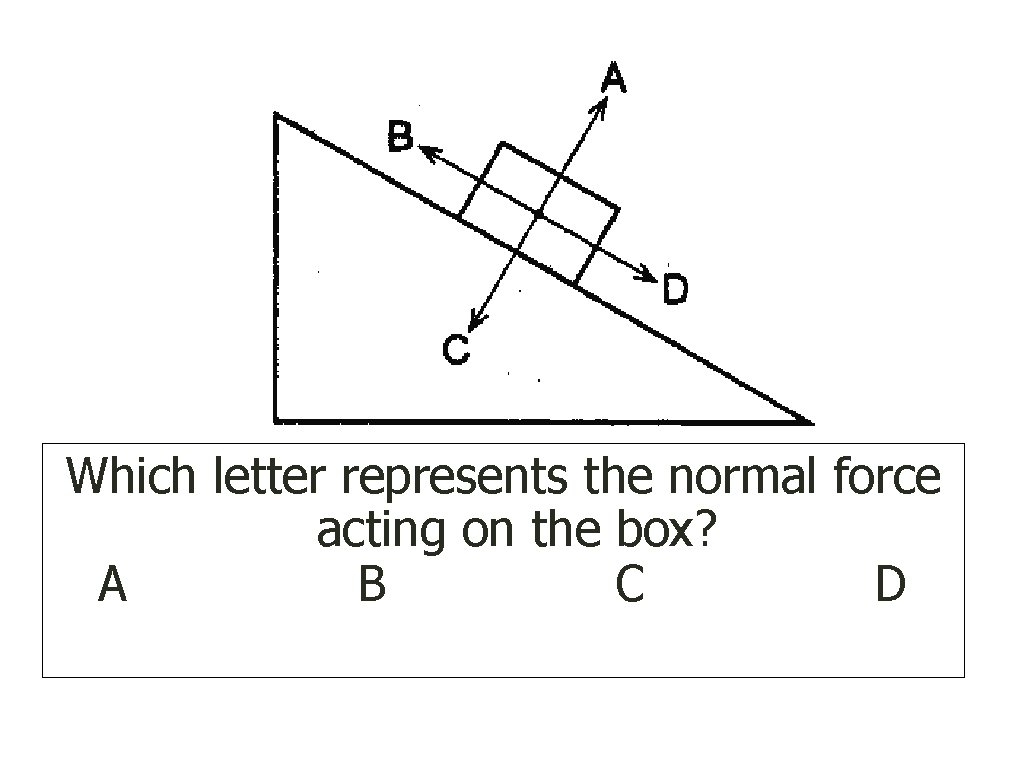
Which letter represents the normal force acting on the box? A B C D

Section wrap-up List an example of each of the following: a. a force causing an object to start moving b. a force causing an object to stop moving c. a force causing an object to change its direction of motion

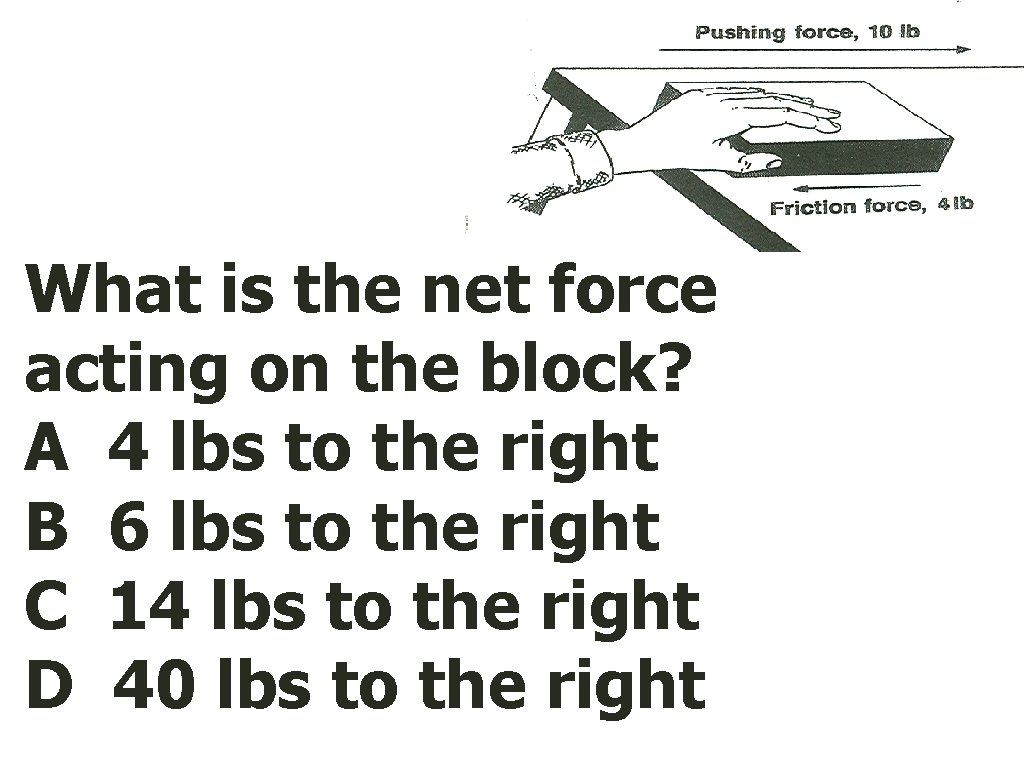
What is the net force acting on the block? A 4 lbs to the right B 6 lbs to the right C 14 lbs to the right D 40 lbs to the right

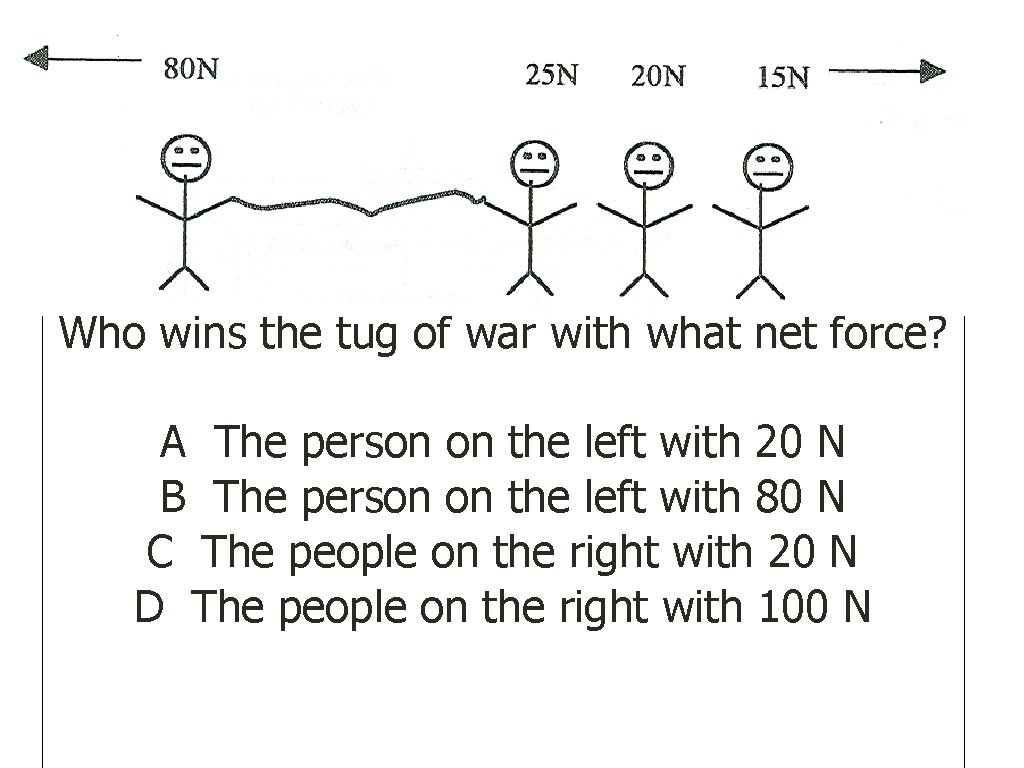
Who wins the tug of war with what net force? A The person on the left with 20 N B The person on the left with 80 N C The people on the right with 20 N D The people on the right with 100 N

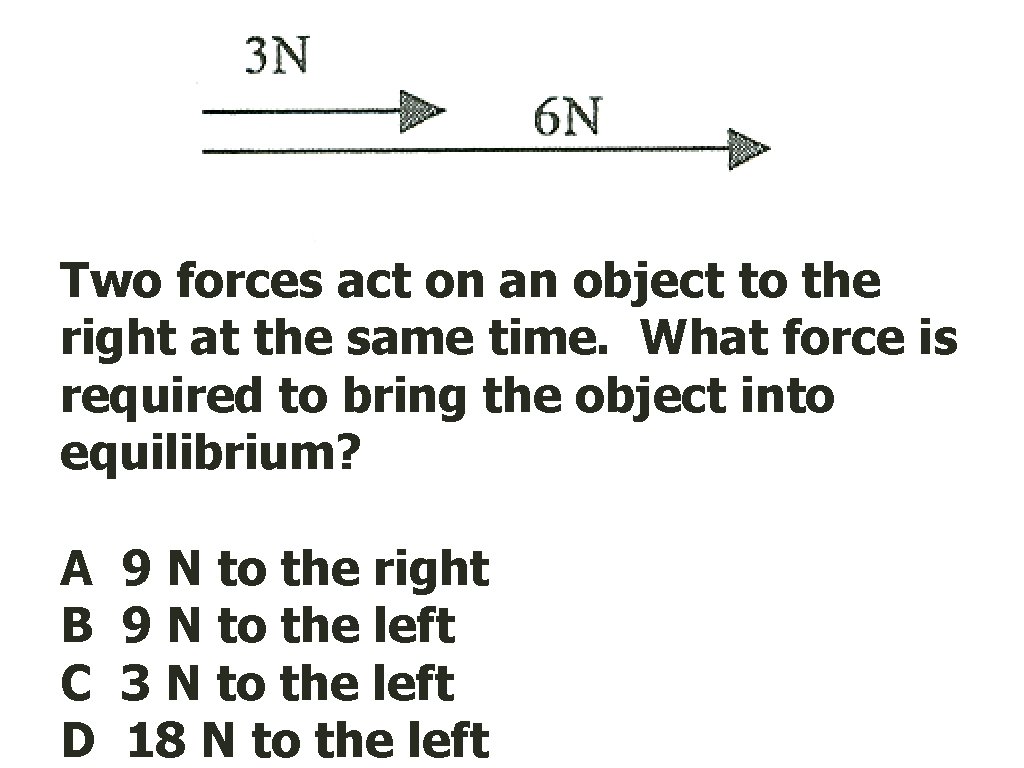
Two forces act on an object to the right at the same time. What force is required to bring the object into equilibrium? A B C D 9 N to the right 9 N to the left 3 N to the left 18 N to the left

If the cart on the right is accelerating, the applied force must be greater than which other force?

If an object is traveling at constant velocity, which two forces will be equal? A. weight and net B. applied and frictional C. net and frictional D. net and applied

The 1 N force most likely represents 5 N 1 N 2 kg 2 N a. gravitational force. b. normal force. c. frictional force. d. net force. What is the net force acting on the object? (Answer must include magnitude, unit, and direction. ) What is its acceleration? (Answer must include magnitude, unit, and direction. )

Newton’s first law of motion can best be used to explain which of the following regarding the ax shown in the picture on the right? A. ax pushes on stump; stump pushes back on ax B. ax remains in stump until an unbalanced force on it C. gravity exerts a force downward; the stump exerts a normal force upward D. the weight of the ax is equal to its mass times acceleration due to gravity

Which of the following objects will require the greatest applied force if all four of the following objects are to be accelerated at the same rate? A. 0. 5 kg ball B. 50 kg motor scooter C. 5 kg rock D. 10 kg box

What is the net force acting on a 2. 0 3 x 10 kilogram car as it accelerates from rest to 15 m/s in 5. 0 seconds? A B C D 3 10 6. 0 x N 4 2. 0 x 10 N 4 3. 0 x 10 N 4 6. 0 x 10 N

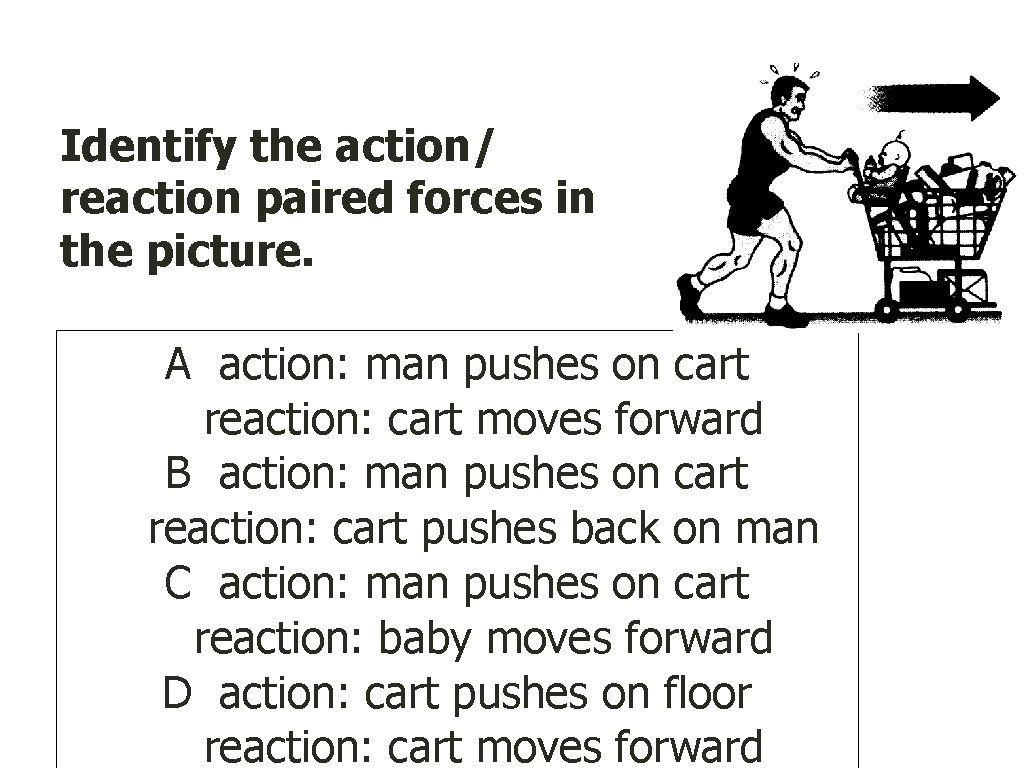
Identify the action/ reaction paired forces in the picture. A action: man pushes on cart reaction: cart moves forward B action: man pushes on cart reaction: cart pushes back on man C action: man pushes on cart reaction: baby moves forward D action: cart pushes on floor reaction: cart moves forward

What is the pair of action/ reaction forces as the boy pushes on the box shown in the picture on the right? A. action: boy pushes on box; reaction: box moves forward B. action: ground pushes up on box; reaction: box moves forward C. action: boy pushes on box; reaction: box pushes back on boy D. action: gravity pulls box downward; reaction: friction works toward the left

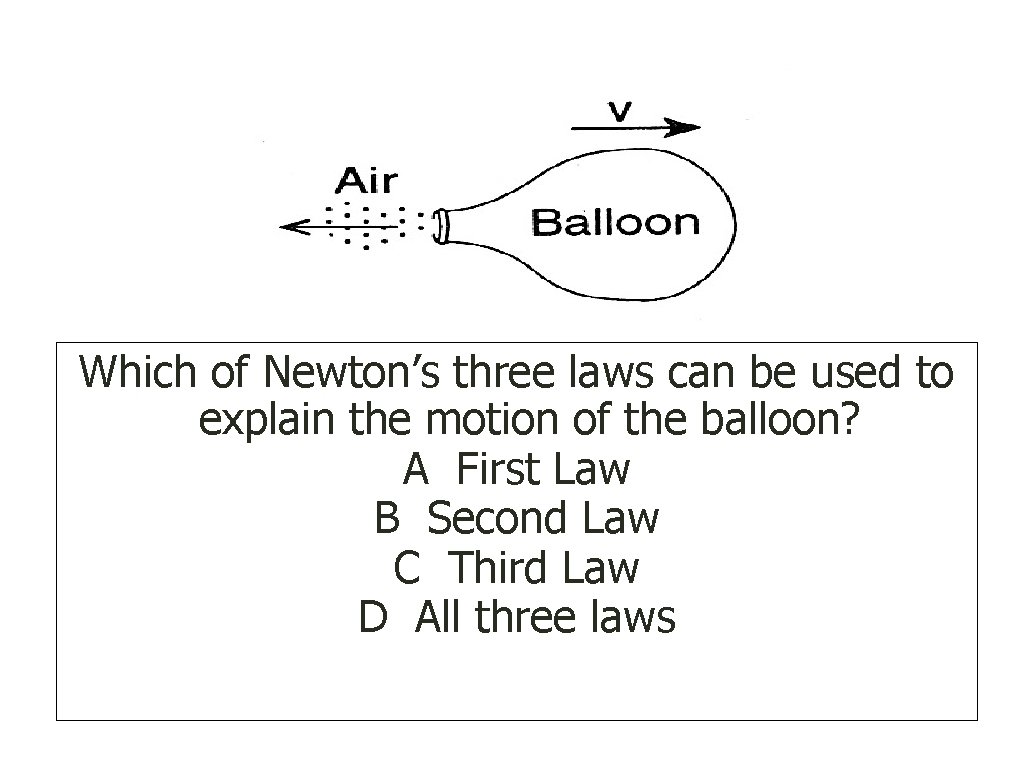
Which of Newton’s three laws can be used to explain the motion of the balloon? A First Law B Second Law C Third Law D All three laws