When Is the Right Time to Refresh Knowledge

When Is the Right Time to Refresh Knowledge Discovered from Data? Xiao (“Shaw”) Fang University of Toledo Olivia R. Liu Sheng University of Utah

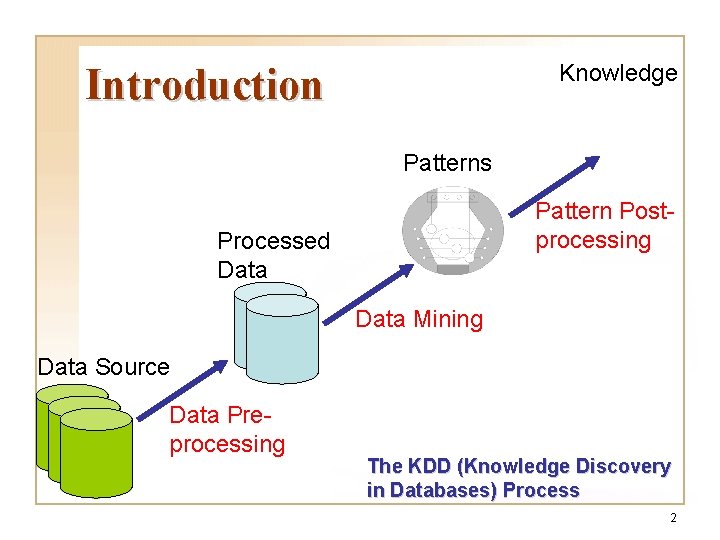
Knowledge Introduction Patterns Pattern Postprocessing Processed Data Mining Data Source Data Preprocessing The KDD (Knowledge Discovery in Databases) Process 2

Introduction q Prior KDD research focused on w efficiency and effectiveness improvement of the KDD process; w innovative applications of KDD. q Prior KDD research overlooked w the problem of maintaining currency of knowledge over an evolving data source 3

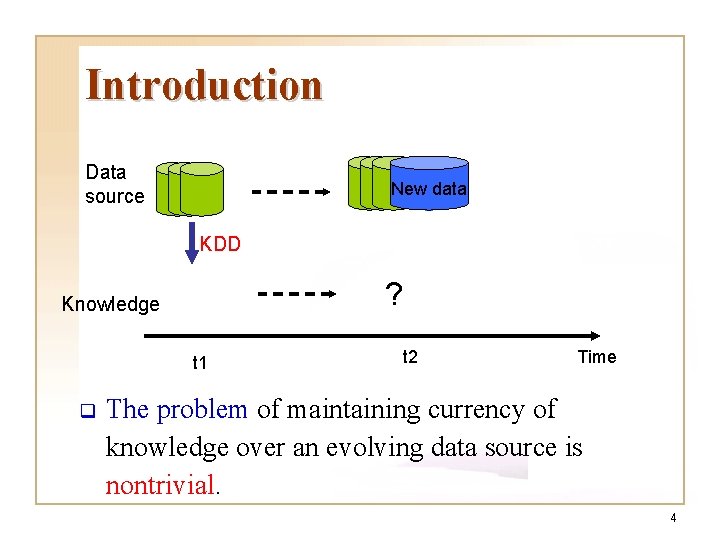
Introduction Data source New data KDD ? Knowledge t 1 q t 2 Time The problem of maintaining currency of knowledge over an evolving data source is nontrivial. 4

Introduction q The problem is a fundamental problem, which impacts every KDD application. q The problem is critical. w Cooper and Giuffrida (2000) w King et al. (2002) 5

Introduction q Knowledge refreshing is an nontrivial process of keeping knowledge discovered using KDD up-to-date with its dynamic data source. 6

Related Work q Incremental q Data data mining stream mining q Related analytical research on databases 7

Related Work Time Manku and Motiwani (2002) Hulten et al. (2001) Guha et al. (2003) 2000 Cheung et al. Utgoff (1989) (1996) Association Classification Can (1993) Data Mining Model Clustering 8

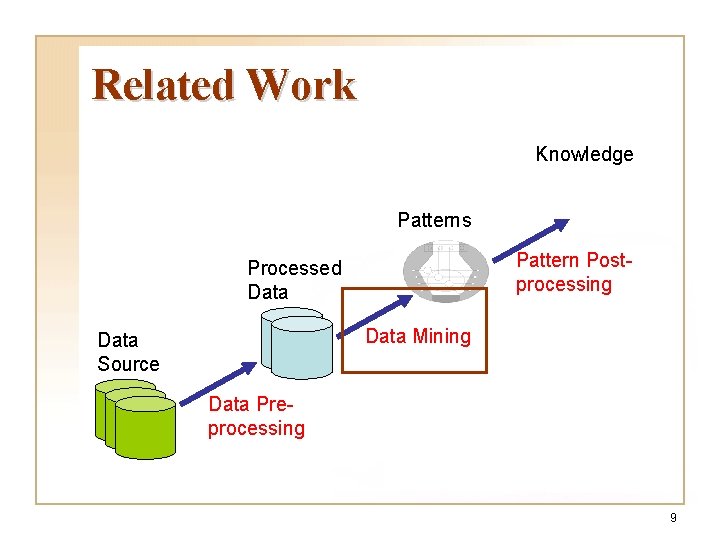
Related Work Knowledge Patterns Pattern Postprocessing Processed Data Mining Data Source Data Preprocessing 9

Related Work q Research gaps: w how to refresh patterns vs. when to refresh knowledge w one step in the KDD process vs. the complete KDD process w one particular data mining model vs. all three major data mining models w computational efficiency vs. effective decision making 10

Related Work q This research studies when to refresh knowledge so as to optimize the trade off between the loss of knowledge and the cost incurred by running KDD. 11

Related Work q Previous analytical research on design and implementation of databases w Chandy et al. (1975) w Park et al. (1990) w Segev and Fang (1991) 12

Related Work q This research is a first study on knowledge refreshing for the KDD process. q The new problem context requires introduction new concepts and new model components, hence, a consequently new model structure. 13

Research Questions q Knowledge loss: what is it? how to measure and estimate it? q The knowledge refreshing problem: definition and model? q Solution and implementation? q How robust and effective is the solution? 14

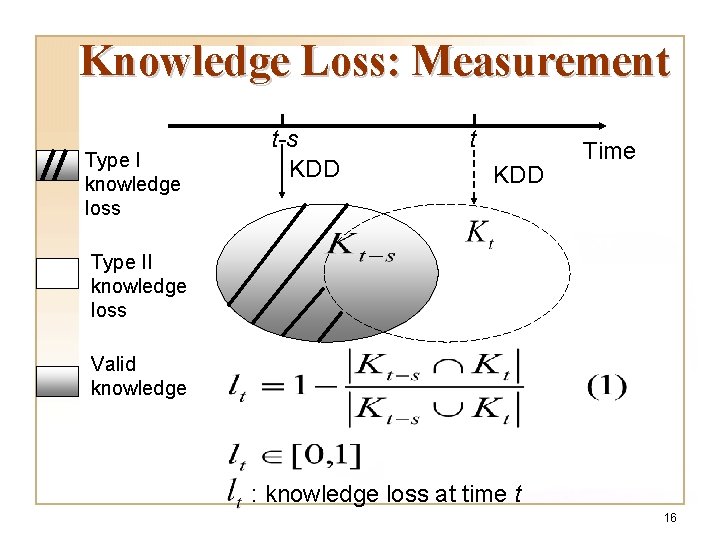
Knowledge Loss: Definition q Knowledge loss refers to the phenomenon that knowledge discovered by a previous run of KDD becomes obsolete gradually as new data are continuously added in. w Type I: part or all of the earlier discovered knowledge become invalid due to incoming new data; w Type II: new knowledge brought in by incoming new data. 15

Knowledge Loss: Measurement Type I knowledge loss t-s KDD t KDD Time Type II knowledge loss Valid knowledge : knowledge loss at time t 16

Knowledge Loss: Measurement q Knowledge discovered by a KDD process employing any of the three major data mining models can be represented as a set. w Association: a set of itemsets or a set of association rules. (Agrawal and Srikant 1994) w Classification: a set of classification rules. (Quinlan 1993) w Clustering: a set of cluster centers. (Jain et al. 1999) 17

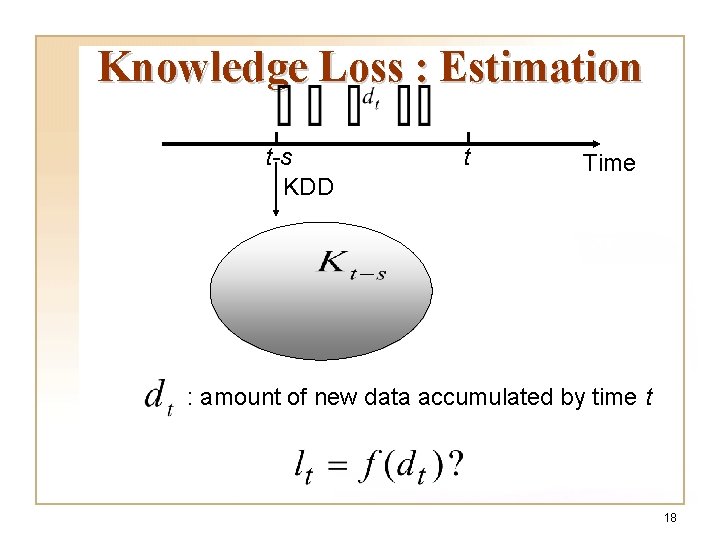
Knowledge Loss : Estimation t-s KDD t Time : amount of new data accumulated by time t 18

Knowledge Loss : Estimation q. A two-parameter Weibull function for estimating knowledge loss 19

Knowledge Loss : Estimation q Motivation Weibull function product degradation in reliability engineering (Murthy et al. 2003) knowledge degradation in KDD q Validation: empirical experiments using real world data 20

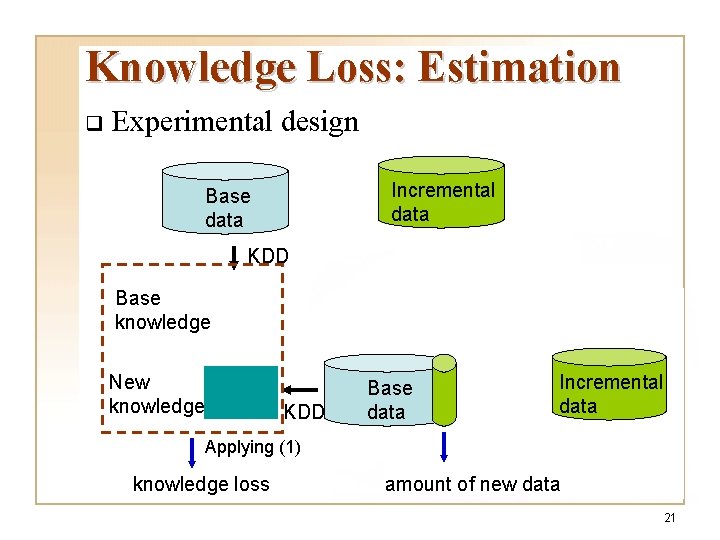
Knowledge Loss: Estimation q Experimental design Incremental data Base data KDD Base knowledge New knowledge KDD Base data Incremental data Applying (1) knowledge loss amount of new data 21

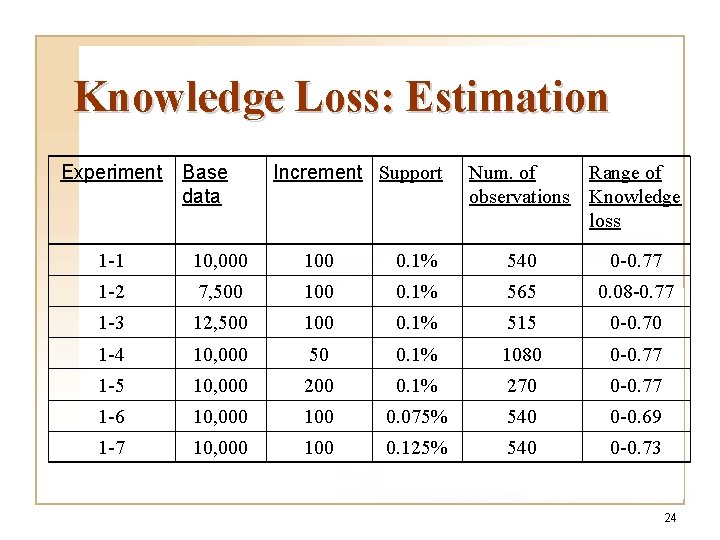
Knowledge Loss: Estimation q Experiment set 1 w Panel data: 63, 999 online transactions w Knowledge discovered: co-purchasing knowledge w Data mining model: Association 22

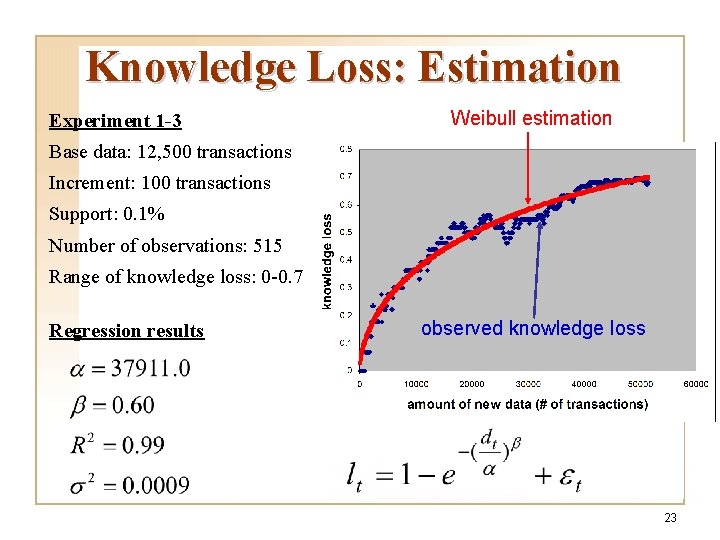
Knowledge Loss: Estimation Experiment 1 -3 Weibull estimation Base data: 12, 500 transactions Increment: 100 transactions Support: 0. 1% Number of observations: 515 Range of knowledge loss: 0 -0. 7 Regression results observed knowledge loss 23

Knowledge Loss: Estimation Experiment Base data Increment Support Num. of Range of observations Knowledge loss 1 -1 10, 000 100 0. 1% 540 0 -0. 77 1 -2 7, 500 100 0. 1% 565 0. 08 -0. 77 1 -3 12, 500 100 0. 1% 515 0 -0. 70 1 -4 10, 000 50 0. 1% 1080 0 -0. 77 1 -5 10, 000 200 0. 1% 270 0 -0. 77 1 -6 10, 000 100 0. 075% 540 0 -0. 69 1 -7 10, 000 100 0. 125% 540 0 -0. 73 24

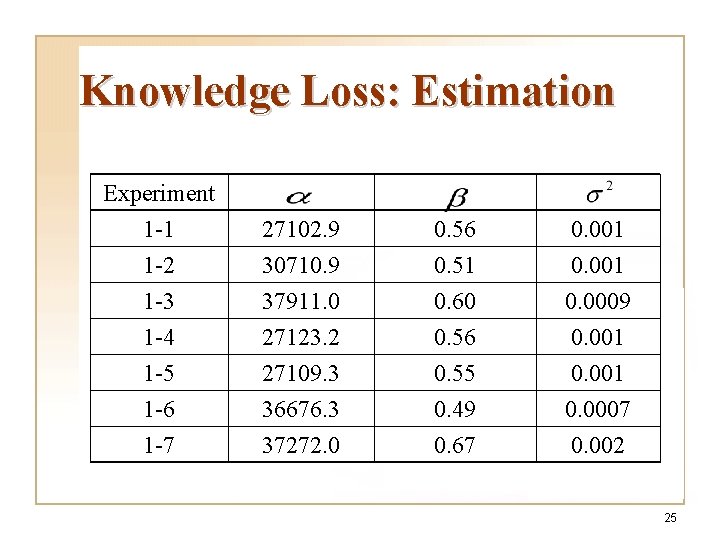
Knowledge Loss: Estimation Experiment 1 -1 1 -2 1 -3 27102. 9 30710. 9 37911. 0 0. 56 0. 51 0. 60 0. 001 0. 0009 1 -4 1 -5 1 -6 1 -7 27123. 2 27109. 3 36676. 3 37272. 0 0. 56 0. 55 0. 49 0. 67 0. 001 0. 0007 0. 002 25

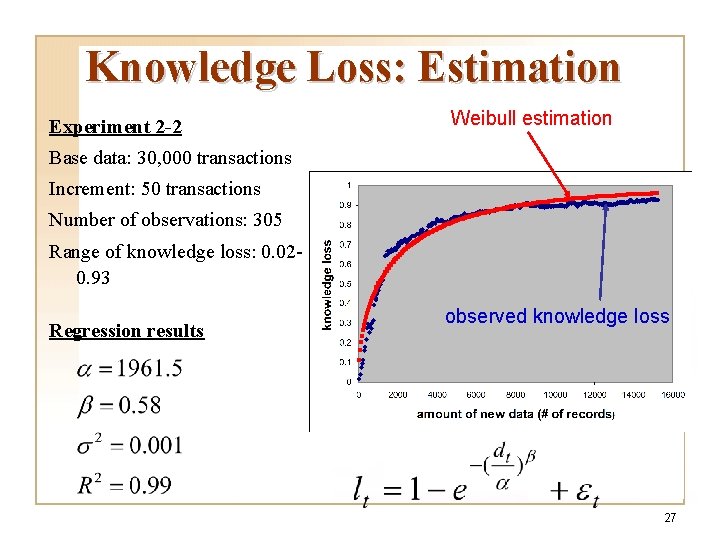
Knowledge Loss: Estimation q Experiment set 2 w Census data (publicly available at the UCI repository for machine learning research): 45, 222 records w Knowledge discovered: rules for predicting income level based on attributes such as age, and education level etc. w Data mining model: Classification 26

Knowledge Loss: Estimation Experiment 2 -2 Weibull estimation Base data: 30, 000 transactions Increment: 50 transactions Number of observations: 305 Range of knowledge loss: 0. 020. 93 Regression results observed knowledge loss 27

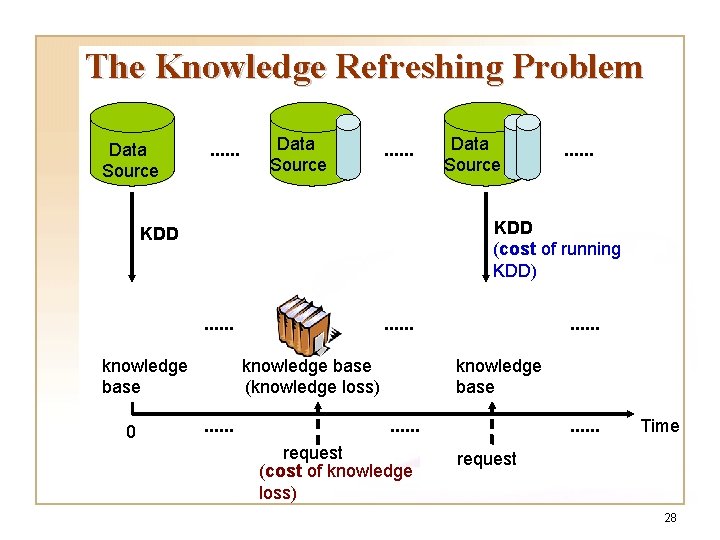
The Knowledge Refreshing Problem Data Source . . . . KDD (cost of running KDD) KDD . . . knowledge base 0 Data Source . . . knowledge base (knowledge loss) . . . knowledge base . . . request (cost of knowledge loss) . . . Time request 28

The Knowledge Refreshing Problem q System constraint: when a request is submitted to the knowledge base, a KDD run is required if current knowledge loss exceeds lc. q The knowledge refreshing problem Determine when to run KDD over a time horizon. Objective: minimize the system cost incurred over the time horizon, subject to the system constraint. 29

Model q Assumption w arrival of new data: following a Poisson process with intensity µ. w n different types of requests: ri , i=1, 2, …, n, n≥ 1. w arrival of type i request: following a Poisson process with intensity λi, i=1, 2, …, n. 30

Model q Decision points: moments when a request arrives. q System time: 0, 1, 2, …, m, …, M M: total number of decision points m: system time of the mth decision point, 1≤m≤M q Action: 0: not running KDD 1: running KDD 31

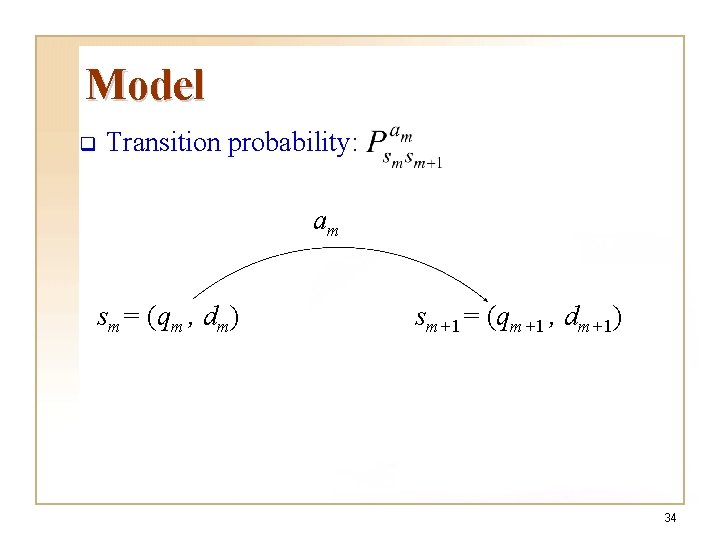
Model q System state: sm=(qm, dm) qm: type of request arrived at time m dm: amount of new data accumulated by time m denotes nonnegative integers 32

Model q System constraint if lm ≥ lc then am = 1, where lm denotes knowledge loss at time m. Applying (2), where 33

Model q Transition probability: am sm= (qm , dm) sm+1= (qm+1 , dm+1) 34

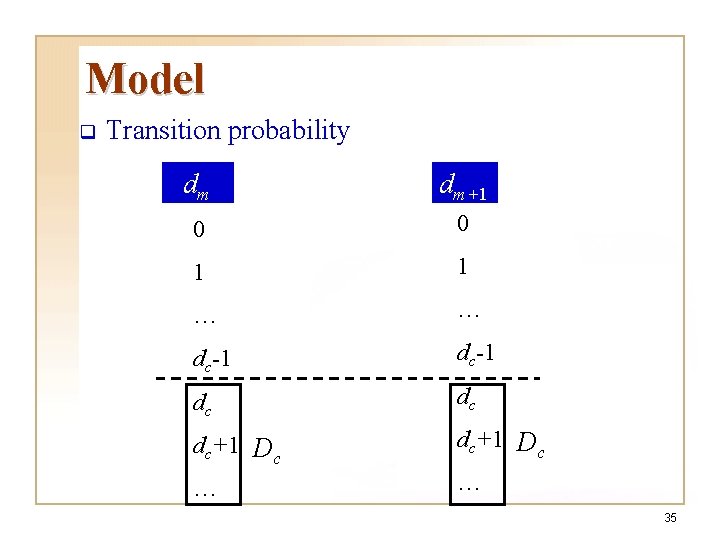
Model q Transition probability dm dm+1 0 0 1 1 … … dc-1 dc dc dc+1 Dc … … 35

Model q Transition probability Lemma 1. The joint probability mass function of and is, 36

Model q Transition probability Lemma 2 37

Model q Transition probability Lemma 2 (continued) 38

Model q Transition probability Lemma 3 39

Model q Transition probability Lemma 3 (continued) 40

Model q Cost function: c(sm, am) q 41

Model q Cost function sm=(qm, dm) lm : cost incurred if a type request is answered from a fully out-of-dated knowledge base (i. e. , knowledge loss is 1) 500 1000 0. 5 1 42

Model q Knowledge refreshing policy: π q Expected system cost under π q The optimal knowledge refreshing policy: π* 43

Solution 0 … 1 m … M : optimal system cost from time m, with state sm , to the end of a time horizon. By the principle of dynamic optimality (Bellman and Dreyfus 1962), 44

Solution q The value iteration method Input Solve (4) from m=M to m=1. Output and the optimal knowledge refreshing policy π* 45

Implementation: the adaptive heuristic q Exponential smoothing method for estimating future data arrival rate 46

Input: Duration of a forward looking period, T Current system state, s Smoothing constant, ω Other system parameters Output: Action Estimate current knowledge loss l using (2) If l ≥ lc a=1 Return a Else Estimate using (5) Estimate using (6) for Approximate M as Derive a 1 by solving (4) from m=M to m=1, given s 1=s a = a 1 Return a End if 47

Numerical Analysis q Simulation design α β 27102. 9 0. 56 µ 348 r 1 λ 1 = 1 cr 1 = 1500 r 2 λ 2 = 1/7 cr 2 = 4500 r 3 λ 3 = 1/14 cr 3 = 18000 ck = 700 (= 20*35) 48

Numerical Analysis q Robustness analysis Generating the optimal knowledge refreshing policy under the Poisson arrival assumption; Implementing the policy in a simulation experiment with exponentially distributed interarrival times of data and requests; Implementing the policy in a simulation experiment with non-exponentially distributed interarrival times of data and requests. 49

Numerical Analysis q Robustness analysis non-exponential distributions selected: w Erlang-4 (coefficients of variation (CV) = 0. 5) w Uniform (CV = 0. 58) w Erlang-2 (CV = 0. 71) w Hyperexponential (CV = 1. 41) 50

Numerical Analysis q Robustness analysis T = 180 lc = 0. 2 =1 Exponential (cost): 62652. 88 Erlang-4 (cost): 63528. 29 1. 4% Uniform (cost): 63168. 46 0. 8% Erlang-2 (cost): 63144. 24 0. 8% Hyperexponential (cost): 63247. 58 1. 0% 51

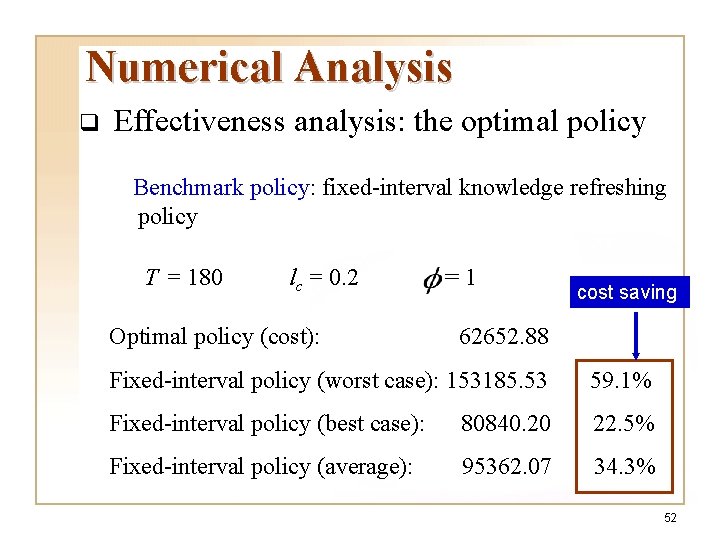
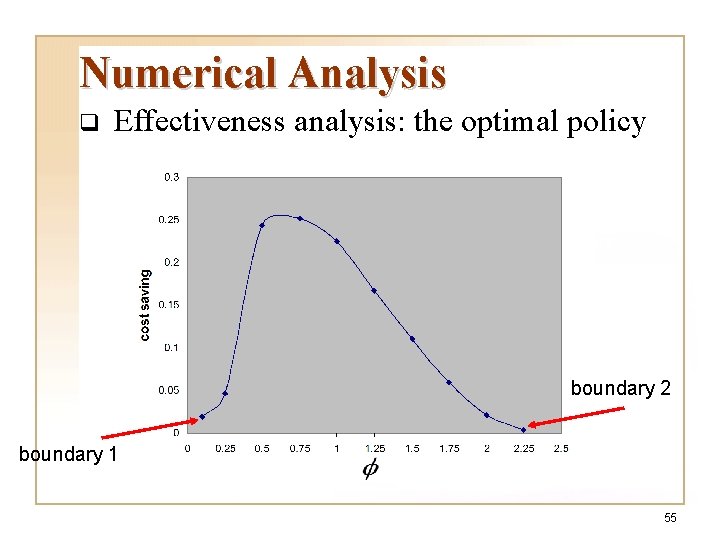
Numerical Analysis q Effectiveness analysis: the optimal policy Benchmark policy: fixed-interval knowledge refreshing policy T = 180 lc = 0. 2 Optimal policy (cost): =1 cost saving 62652. 88 Fixed-interval policy (worst case): 153185. 53 59. 1% Fixed-interval policy (best case): 80840. 20 22. 5% Fixed-interval policy (average): 95362. 07 34. 3% 52

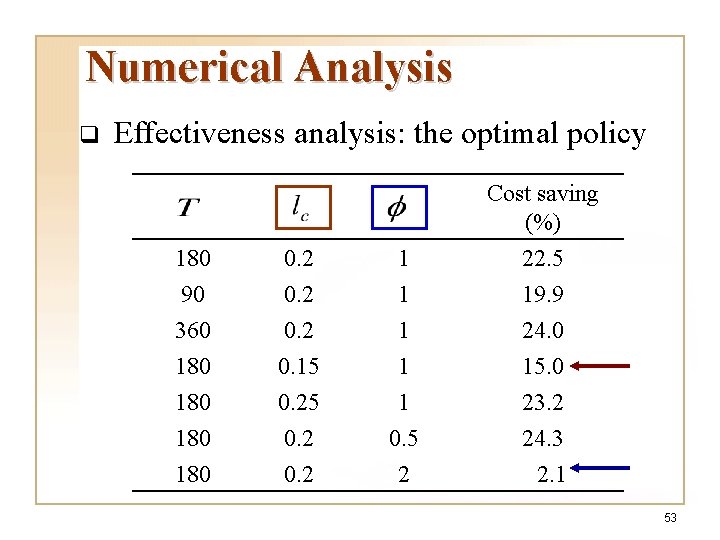
Numerical Analysis q Effectiveness analysis: the optimal policy Cost saving (%) 180 90 0. 2 1 1 22. 5 19. 9 360 180 180 0. 2 0. 15 0. 2 1 1 1 0. 5 2 24. 0 15. 0 23. 2 24. 3 2. 1 53

Numerical Analysis q Effectiveness analysis: the optimal policy Cost saving (%) Percentage of KDD runs enforced by the system constraint (%) 0. 05 0. 1 98. 5 0. 1 5. 3 88. 1 0. 15 15. 0 64. 4 0. 2 22. 5 25. 6 0. 25 23. 2 0. 1 0. 3 24. 0 0 0. 35 24. 0 0 54

Numerical Analysis q Effectiveness analysis: the optimal policy boundary 2 boundary 1 55

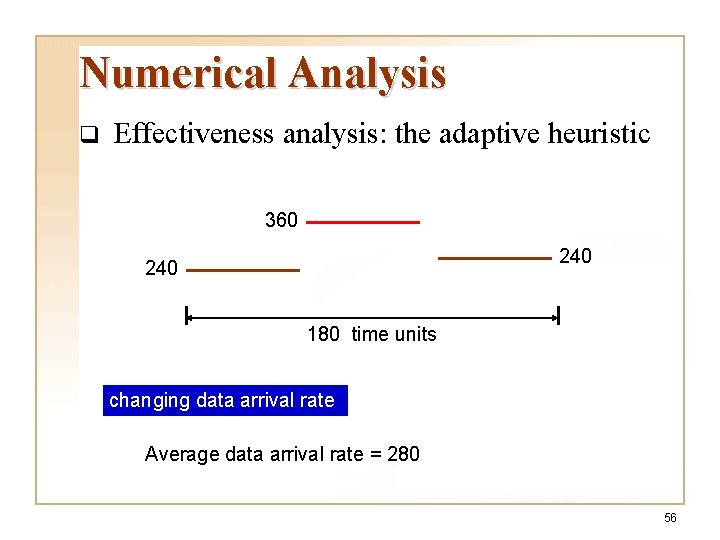
Numerical Analysis q Effectiveness analysis: the adaptive heuristic 360 240 180 time units changing data arrival rate Average data arrival rate = 280 56

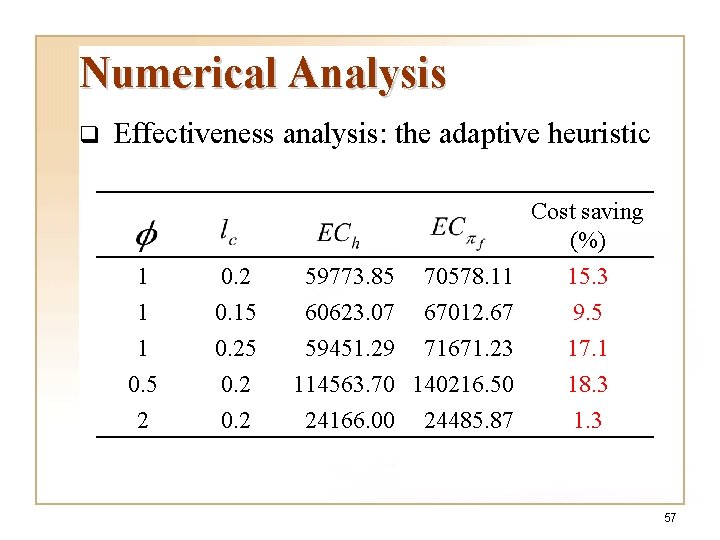
Numerical Analysis q Effectiveness analysis: the adaptive heuristic Cost saving (%) 1 1 1 0. 5 2 0. 15 0. 2 59773. 85 70578. 11 60623. 07 67012. 67 59451. 29 71671. 23 114563. 70 140216. 50 24166. 00 24485. 87 15. 3 9. 5 17. 1 18. 3 1. 3 57

Contributions q This research is a first study on knowledge refreshing, an ubiquitous problem faced by every KDD application. q We introduce the concept of knowledge loss. We also propose how to measure and estimate knowledge loss. q We propose a general model for knowledge refreshing and derive from the model an optimal policy and an adaptive heuristic for knowledge refreshing. 58

Contributions q The measurement and estimating functions of knowledge loss can be employed to assess the quality of a knowledge base. q The adaptive heuristic is readily applicable for solving real word knowledge refreshing problems. 59

Future Research q Theoretical foundations for the estimating function of knowledge loss. q Multiple system constraints. q Boundary conditions under which a bestperformed fixed-interval policy is as good as an optimal policy. 60

Comments and Suggestions 61