WHATS THE DIFFERENCE Undilated Dilated VOCABULARY Dilation a

WHAT’S THE DIFFERENCE? ? Undilated Dilated

VOCABULARY Dilation: a transformation that changes the size of a figure but NOT its shape. Similar: Two figures are similar if they have the same shape but not necessarily the same size. Scale Factor: Describes how much the figure is enlarged or reduced. Represented by the letter K You can find the image of a point by multiplying each coordinate by k.

TO FIND THE COORDINATES OF THE NEW IMAGE AFTER A DILATION: 1. Multiply each x and y-coordinate in each of the ordered pairs by the given scale factor K. 2. Then connect the vertices of the new ordered pairs.

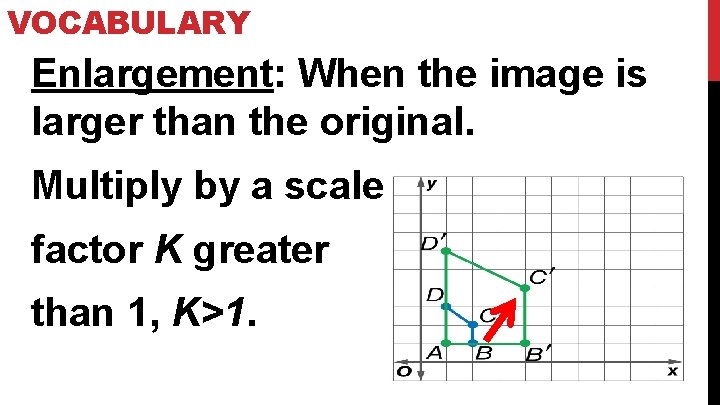
VOCABULARY Enlargement: When the image is larger than the original. Multiply by a scale factor K greater than 1, K>1.

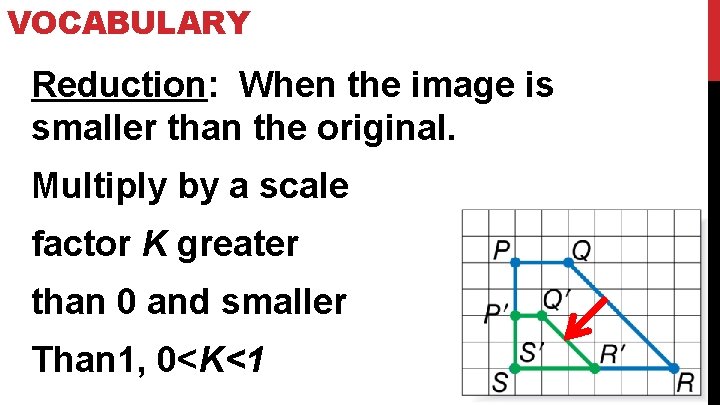
VOCABULARY Reduction: When the image is smaller than the original. Multiply by a scale factor K greater than 0 and smaller Than 1, 0<K<1

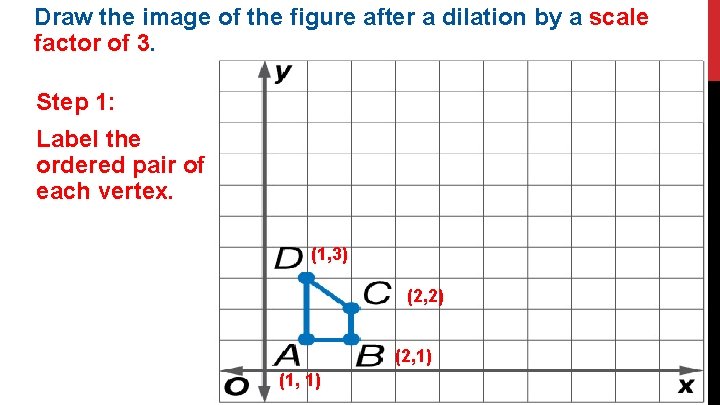
Draw the image of the figure after a dilation by a scale factor of 3. Step 1: Label the ordered pair of each vertex. (1, 3) (2, 2) (2, 1) (1, 1)

Step 2: Multiply each coordinate in the ordered pairs by the scale factor 3. A(1, 1) (1● 3, 1● 3) A’(3, 3) B(2, 1) (2● 3, 1● 3) B’(6, 3) C(2, 2) (2● 3, 2● 3) C’(6, 6) D(1, 3) (1● 3, 3● 3) D’(3, 9)

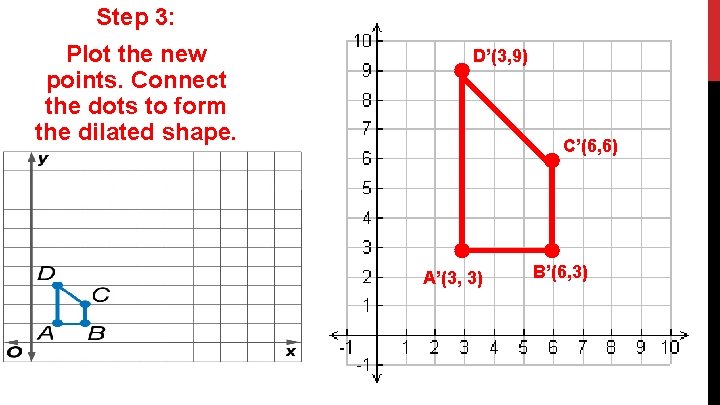
Step 3: Plot the new points. Connect the dots to form the dilated shape. D’(3, 9) C’(6, 6) A’(3, 3) B’(6, 3)

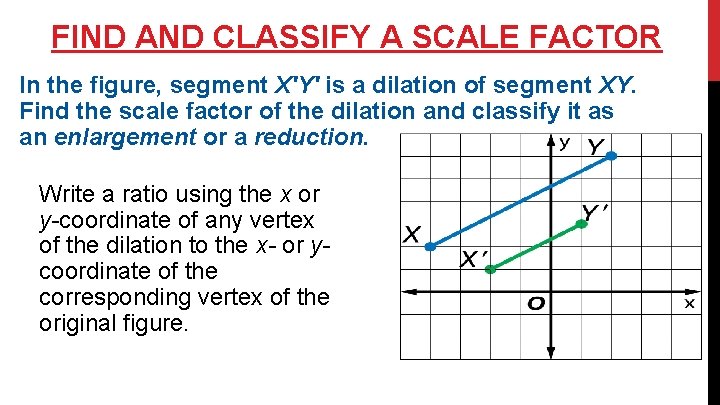
FIND AND CLASSIFY A SCALE FACTOR In the figure, segment X'Y' is a dilation of segment XY. Find the scale factor of the dilation and classify it as an enlargement or a reduction. Write a ratio using the x or y-coordinate of any vertex of the dilation to the x- or ycoordinate of the corresponding vertex of the original figure.

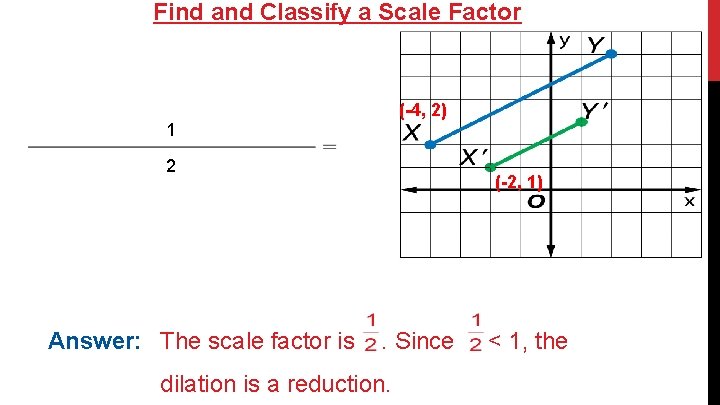
Find and Classify a Scale Factor (-4, 2) 1 2 Answer: The scale factor is (-2, 1) . Since dilation is a reduction. < 1, the

STOP HERE WE WILL COVER THE FOLLOWING INFORMATION DURING THE NEXT CLASS.

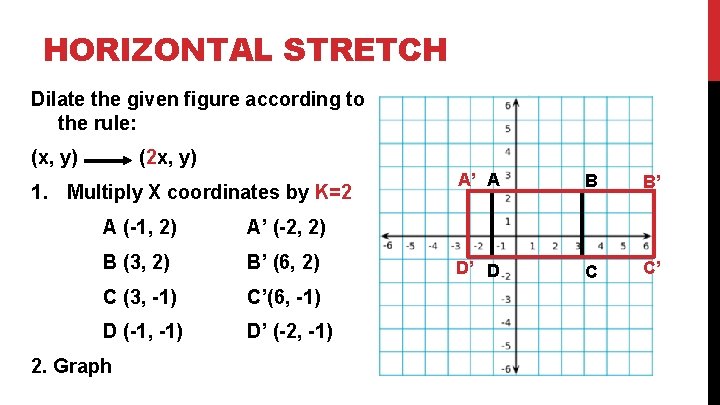
HORIZONTAL STRETCH Dilate the given figure according to the rule: (x, y) (2 x, y) 1. Multiply X coordinates by K=2 A (-1, 2) A’ (-2, 2) B (3, 2) B’ (6, 2) C (3, -1) C’(6, -1) D (-1, -1) D’ (-2, -1) 2. Graph A’ A B B’ D’ D C C’

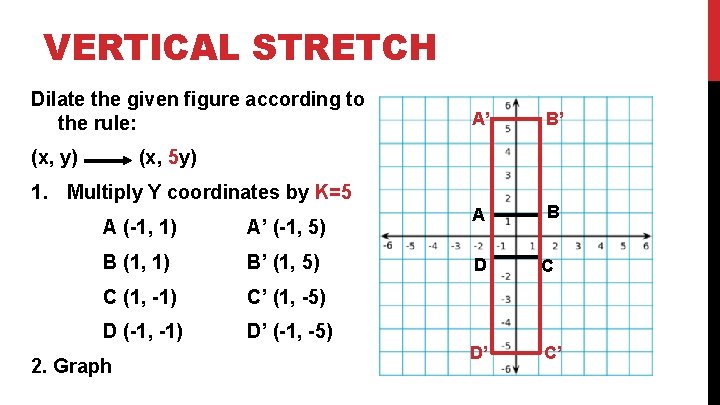
VERTICAL STRETCH Dilate the given figure according to the rule: (x, y) A’ B’ A B (x, 5 y) 1. Multiply Y coordinates by K=5 A (-1, 1) A’ (-1, 5) B (1, 1) B’ (1, 5) C (1, -1) C’ (1, -5) D (-1, -1) D’ (-1, -5) 2. Graph D C D’ C’

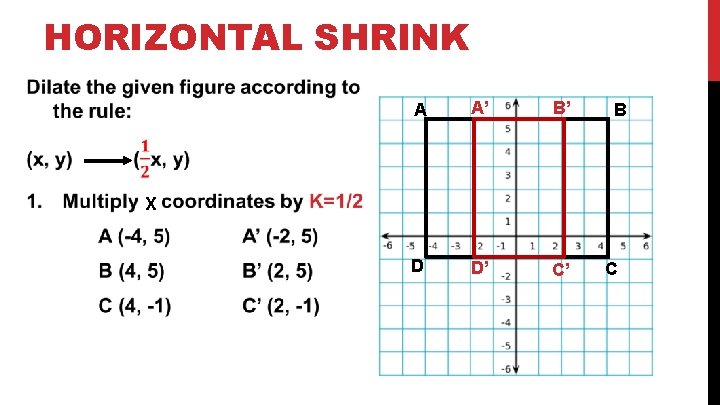
HORIZONTAL SHRINK A A’ B’ D D’ C’ B X C

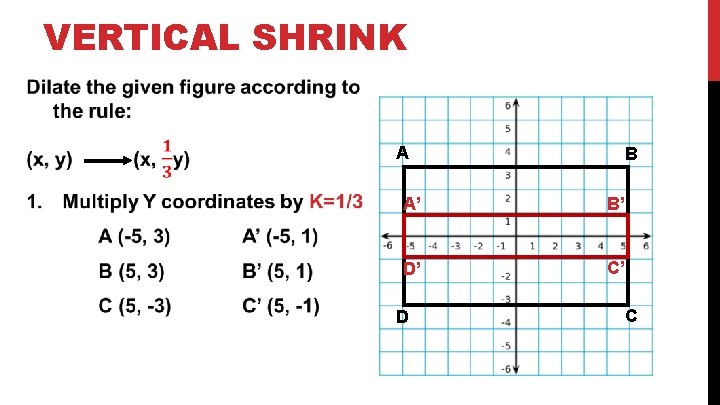
VERTICAL SHRINK A B A’ B’ D’ C’ D C

IF YOU NEED MORE HELP WATCH THE VIDEOS http: //www. mathwarehouse. com/transformations/dil ations-in-math. php http: //www. mathworksheetsland. com/geometry/16 dilation/ip. pdf http: //www. mathworksheetsland. com/geometry/1 geo-16 -2. pdf