Whats so special about this little triangle and

What’s so special about this little triangle and its pattern of numbers? In this investigation, you’ll discover the answer to that question along with some amazing mathematics!

o. Blaise Pascal was a natural genius who lived from 1623 to 1662. He was born in Clermont, France. o. His father oversaw his son’s studies at home. He confined Pascal to the study of languages and directed that his studies should not include any mathematics. o. This only excited his curiosity more and at the age of twelve, he began to explore geometry and made some great discoveries! His father gave him a copy of Euclid’s book, called Elements, which he mastered quickly! o. As an adult he abandoned the study of math for awhile and became curious about religion. But in 1653, he invented the arithmetical triangle that we are about to begin studying. o. Throughout this presentation, you’ll learn about and explore this amazing triangle and its many mathematical connections!

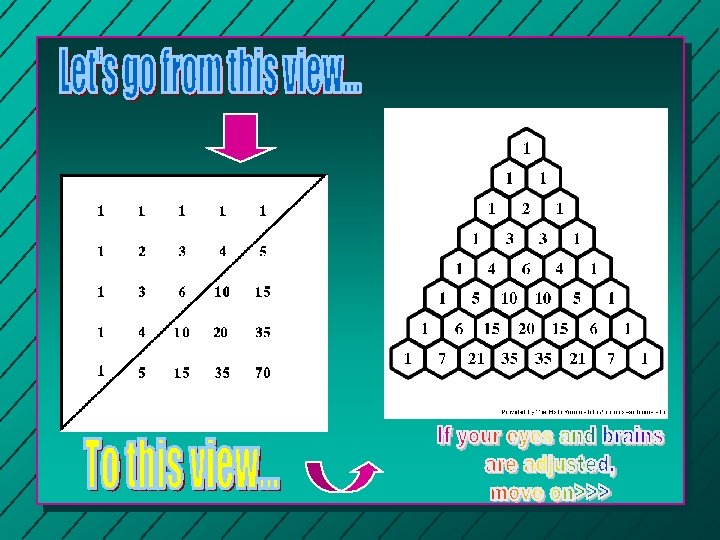
> In this view of the triangle, you get a first look at Pascal’s discovery. He wrote “figurate” numbers (more on this later!) >On the first line, are written numbers of the first order. The second line are the natural numbers or numbers of the 2 nd order. >On the third line are numbers of the third order and so on. Do you remember anything special about these numbers. If not, you’ll be reminded soon! >This triangle had so many patterns and mathematical connections to algebra, geometry, probability that it amazes all who take time to explore it!

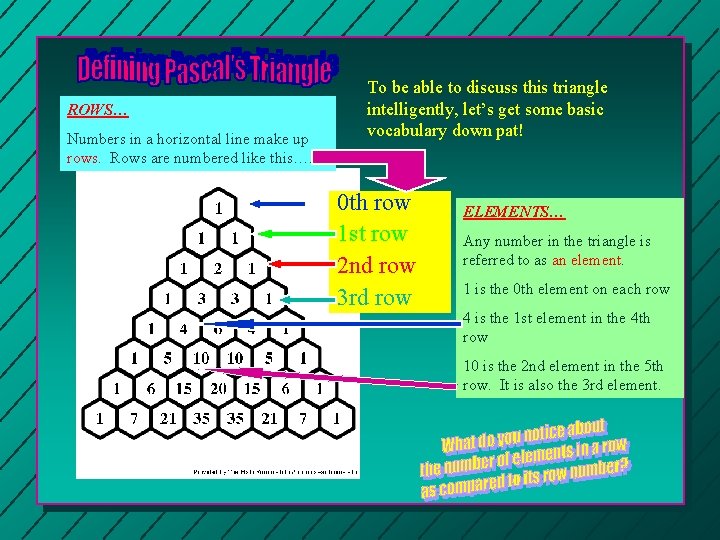
ROWS… Numbers in a horizontal line make up rows. Rows are numbered like this…. To be able to discuss this triangle intelligently, let’s get some basic vocabulary down pat! 0 th row 1 st row 2 nd row 3 rd row ELEMENTS… Any number in the triangle is referred to as an element. 1 is the 0 th element on each row 4 is the 1 st element in the 4 th row 10 is the 2 nd element in the 5 th row. It is also the 3 rd element.

1 st: Can you figure out the pattern that helps to create each new row? How would you describe it? Click here when you are ready to check your answer The sum of two adjacent numbers is equal to the number directly below it and between them! (I bet you said it just like this! You are a genius!)

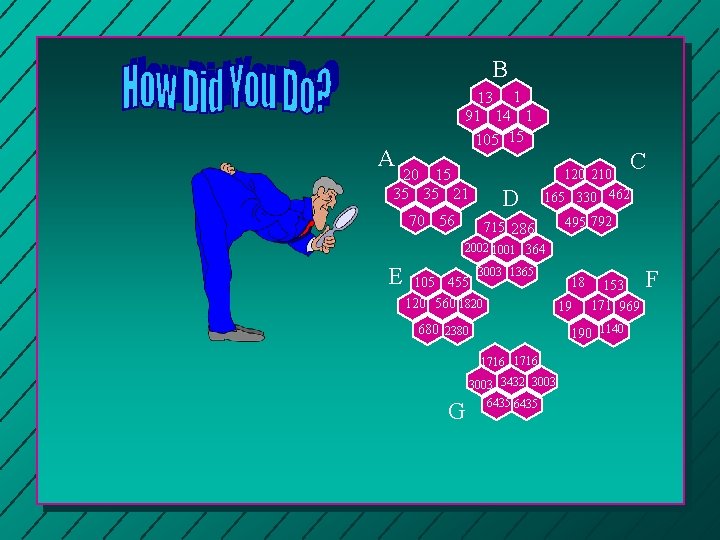
B 91 14 1 A What you see are portions of Pascal’s Triangle. Can you use what you know already to be able to fill in the missing numbers? C 15 35 35 56 E 120 210 462 D 715 286 3003 1365 105 120 560 1820 495 153 171 190 1140 1716 3003 G 3003 F

In this next set of activities, you’ll be searching for the patterns found when finding sums in Pascal’s triangle! Recall: what is a row? How are they numbered? Directions: Fill in the table below by finding the sum of the elements in the first few rows of Pascal’s triangle. See if you can answer the questions using the pattern you may discover! Row 0 1 2 3 4 5 6 Row Sum 1 2 • What is the pattern of the sums? • How could you relate the row number to the sum of that row? • How would you express the sum of the elements in the 20 th row? In the 100 th row? , in the nth row?

Shift your eyes to looking at the diagonals now, instead of the rows! ¨Where is the element that will give the sum of the first 4 elements of the first diagonal (1+2+3+4)? ¨Where is the element that will give the sum of the first 4 elements of the second diagonal (1+3+6+10)? ¨What is the pattern that will give the sum of any number of elements in any diagonal?

The sum of the first 4 elements of the 2 nd diagonal (1+2+3+4) can be found in the 4 th (how many elements you were adding) position of the 3 rd diagonal ( adjacent to the 2 nd diagonal where you were adding) What is the pattern that will give the sum of any number of elements in any diagonal? Answer: The sum of any number of elements in any diagonal can be found by looking for the element in the next adjacent diagonal which has the same position number as the number of elements you were adding!

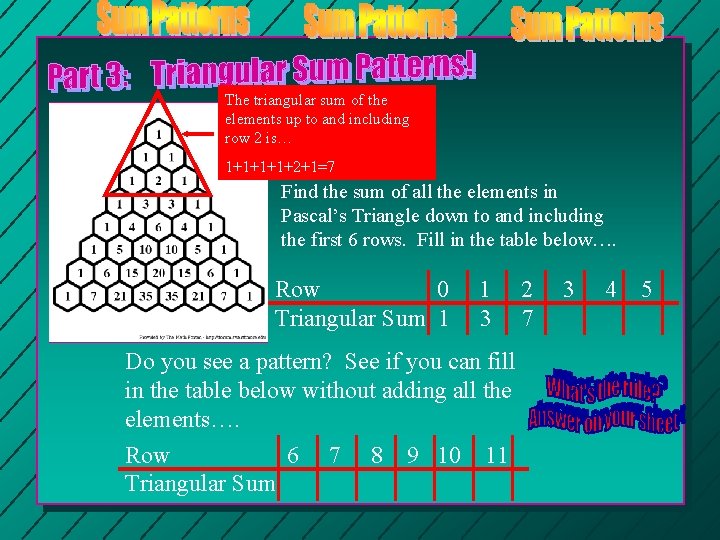
The triangular sum of the elements up to and including row 2 is… 1+1+2+1=7 Find the sum of all the elements in Pascal’s Triangle down to and including the first 6 rows. Fill in the table below…. Row 0 Triangular Sum 1 1 3 Do you see a pattern? See if you can fill in the table below without adding all the elements…. Row 6 7 8 9 10 11 Triangular Sum 2 7 3 4 5

PGet a copy of a filled in Pascal Triangle. / / PWork in groups of 4. PHave one member of your group color in all the multiples of 3. PHave another member color in all the multiples of 5 PAnother member fills in all the multiples of 7 PThe last member of the group fills in all the multiples of 9 PDo you see a pattern? What is different about the pattern with the multiples of 9? Can you figure out what it is about 3, 5 and 7 that causes this pattern and why it doesn’t continue at 9? Does it continue with other numbers larger than 9? Check out an interesting web site at : http: //www. cs. washington. edu/homes/jbaer/classes/blaise. html

/ / Download a copy of a Pascal worksheet from http: //mathforum. com/workshops/usi/pascal/mid. color_pascal. html POpen a Pascal worksheet in the Claris. Works paint program. PChoose you favorite color from the paint palette and using the divisibility rule for 3, paint all the cells that contain a multiple of 3. PChoose another color and paint all the cells that contain one less than a multiple of 3 with this color. PChoose another color and paint all the cells that contain two less than a multiple of 3 with this color. PDo you see a pattern? PCan you see any “symmetry” in the design? PCopy your design into a drawing program, duplicate it 6 times and link it together to create a hexagon. P Look at the center point where they are joined. Can you see the optical illusion of a cube?

Notice the seven elements grouped together. This group is known as a Pascal flower. The middle cell of 15 is surrounded by 6 cells called petals. Starting with the petal above and to the left of 15, the alternating petals are highlighted in red and are numbered 5, 20, and 21. The three remaining petals are highlighted in yellow and contain the numbers 10, 35, and 6 • Find the product of the red petals. Find the product of the yellow petals. What do you notice? Can you explain this? • Write the prime factorization of the numbers in the red petals. Write the prime factorization of the numbers in the yellow petals. Compare the two prime factorizations. Share your discovery! • See if it works with any other Pascal flower!

What is 11 to the 0 th power? What is 11 to the 1 st power? What is 11 to the 2 nd power? What is 11 to the 3 rd power? Where can you find these answers in Pascal’s triangle? Click here to check

What is 11 to the 0 th power? What is 11 to the 1 st power? What is 11 to the 2 nd power? What is 11 to the 3 rd power? Where can you find these answers in Pascal’s triangle? 11 to any power is found by using the digits in the row that has the same power number!

Do you remember the Fibonacci Sequence, (1, 1, 2, 3, 5, 8, 13, …. ) where each term is the sum of the two previous terms? This sequence can be found in Pascal’s triangle by following “shadow diagonals” See below for the illustration

Do you remember the triangular numbers? These numbers are created by thinking of the number of dots you need to make a triangle. These numbers are found in the third diagonal of Pascal’s triangle!

Pascal’s triangle is found with many more interesting number patterns such as …. . To explore these kinds of numbers in Pascal’s triangle, visit the website found at : http: //forum. swarthmore. edu/workshops/usi/pascal_numberpatterns. html

Remember solving problems involving combinations…. they were like this…. . If I have 3 different socks, how many different ways could I choose 2 of them. Using a list where a, b, and c are the different socks, I see I have three possibilities… ab, ac, and ac. This answer and answers to all types of “combination” problems are found in Pascal’s triangle! Watch! Since there are 3 items to choose from, go to row 3! Since you are choosing only 2 items, go to the 2 nd element in that row and find your answer!

Use the information from the previous slide, and Pascal’s triangle to help you answer this question! What is the probability of choosing one combination of two colors if you have 5 colors to choose from? Use the triangle to help you, give your probability answer as a fraction! When ready, click on the arrow below to check! The total number of combinations of 2 items that can be made from 5 items is found in the 2 nd element of the 5 th row! Therefore the probability of choosing one combination is 1/10!

This great problem was found on the www at http: //forum. swarthmore. edu/workshops/usi/pascal/pizza_pascal. html Use what you learned from the previous slides to answer the questions following the story of Antonio’s Pizza Palace. It’s Friday night and the Pizza Palace is more crowded than usual. At the counter the Pascalini’s are trying to order a large pizza, but can’t agree on what toppings to select. Antonio, behind the counter, says, “I only have 8 different toppings. It can’t be that hard to make up your mind. How many different pizzas can that be? ” “Well, we could get a plain pizza with no toppings, ” says Mr. . Pascalini. “Or we could get a pizza with all 8 toppings, ” says Mrs. . Pascalini.

“What about a pizza with extra cheese and green peppers? ” asks Pepe. “You’re not helping!” Antonio yells at Pepe. “Get back to work!” As Pepe starts to clear off the nearest table, he mumbles to himself, “or a pizza with anchovies, extra cheese, mushrooms and olives. ” Antonio hands an order pad to Mr. . Pascalini and says, “When you decide, write it down and I’ll make it. ” Then he helps the next people in line , who know what they want: a large pizza with mushrooms, green peppers and tomatoes.

How many different pizzas can be ordered at the Pizza Palace if a pizza can be selected with any combination of the following toppings: anchovies, extra cheese, green peppers, mushrooms, olives, pepperoni, sausage, and tomatoes? As you solve the problem, look for patterns and answer the following questions: 1. How many different pizza can you order with only one topping? 2. How many different pizzas can you order each with seven toppings? 3. Are the number of one-topping pizzas and the number of seven-topping pizzas related? (Why or why not? ) 4. How many different pizzas can you order with two toppings? 5. How many different pizzas can you order with six toppings? 6. Are the number of two-topping pizzas and the number of six-topping pizzas related? (Why or why not? )

That’s all, folks!!!! I hope you enjoyed investigating my special little triangle and that you made many mathematical discoveries. But for now…. . .

B 13 1 91 14 1 105 15 A 20 15 35 35 21 70 56 E D 715 286 2002 1001 364 3003 1365 105 455 120 560 1820 680 2380 495 792 18 19 153 171 969 190 1140 1716 G C 120 210 165 330 462 3003 3432 3003 6435 F

Row Sum 0 1 2 3 4 5 6 1 2 4 8 16 32 64 Did you discover…. ? • The pattern of the sums forms the sequence of the powers of 2. • The sum of any row is equal to 2 to the row power 20 • The sum of the 20 th row is 2 100 • The sum of the 100 th row would be 2 • The sum of the nth row would be 2 n

Find the sum of all the elements in Pascal’s Triangle down to and including the first 6 rows. Fill in the table below…. Row 0 Triangular Sum 1 1 3 2 7 3 4 5 15 31 63 Do you see a pattern? See if you can fill in the table below without adding all the elements…. Row 6 7 8 9 10 11 Triangular Sum 127 254 511 1023 2047 4095 The triangular sum of any number of rows is equal to (2 (Row Number +1) - 1)

What did you discover? Share your discovery with the class! Click below to see how Pascal’s triangle can solve this problem! Pascal’s Triangle solves this problem by adding all of the elements in the 8 th row. . . 1+8+28+56+70+56+28+8+1= 256 possible pizzas!