What to measure when measuring noise in MRI

What to measure when measuring noise in MRI Santiago Aja-Fernández sanaja@tel. uva. es Antwerpen 2013

Noise in MRI Motivation: • • Many papers and methods to estimate noise out of MRI data. Noise estimation vs. SNR estimation In single coil systems, variance of noise is a “good” measure. Complex systems: what are we really measuring? Is the variance of noise still valid? 2

Noise in MRI Outline 1. Noise in MR acquistions 2. Basic Models – Rician – Non-central chi 3. More Complex Models – Correlated multiple coils – Parallel MRI: SENSE and GRAPPA 4. The nc-chi example – Non-stationary noise – Effective values 5. Other models 6. Conclusions 3

Noise in MRI 4

Noise in MRI 5

Noise in MRI 1 - Noise in MRI 6

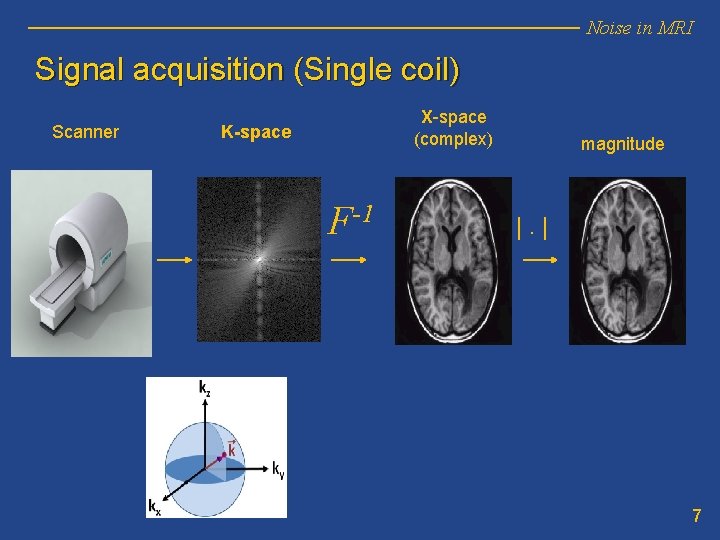
Noise in MRI Signal acquisition (Single coil) Scanner X-space (complex) K-space F-1 magnitude |. | 7

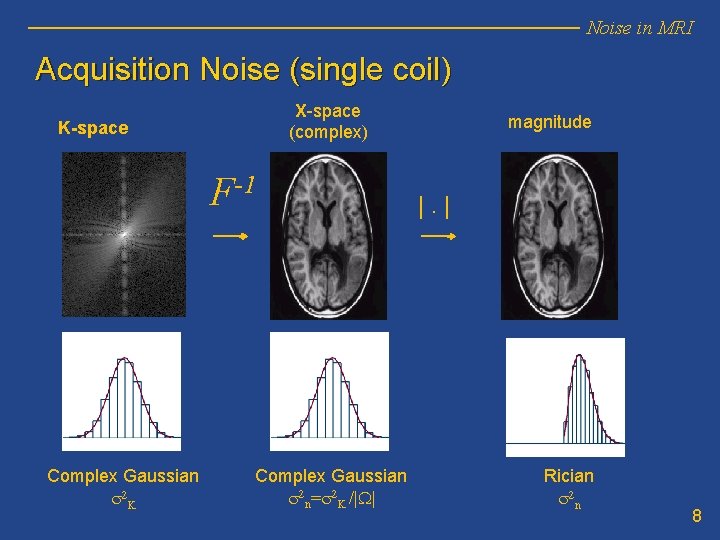
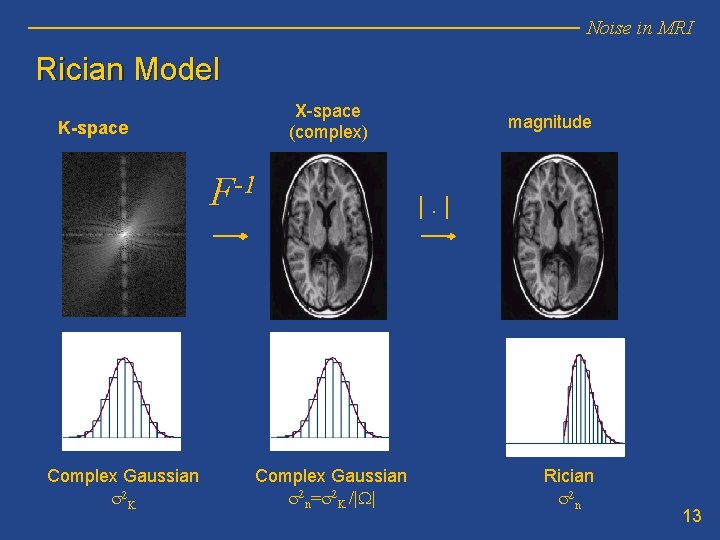
Noise in MRI Acquisition Noise (single coil) X-space (complex) K-space F-1 Complex Gaussian s 2 K Complex Gaussian s 2 n=s 2 K /|W| magnitude |. | Rician s 2 n 8

Signal acquisition (Multiple coil) Noise in MRI F-1 9

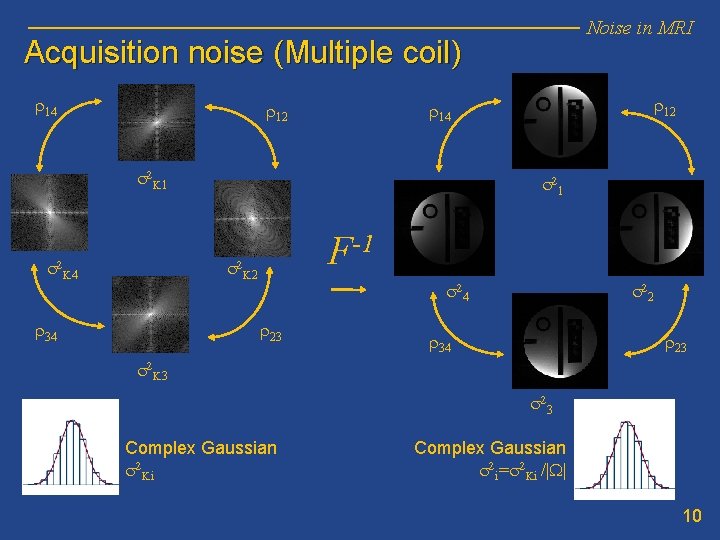
Noise in MRI Acquisition noise (Multiple coil) r 14 r 12 s 2 K 1 s 2 K 4 s 2 1 F-1 s 2 K 2 r 34 r 12 r 14 s 2 4 r 23 s 2 2 r 34 r 23 s 2 K 3 s 2 3 Complex Gaussian s 2 Ki Complex Gaussian s 2 i=s 2 Ki /|W| 10

Noise in MRI Acquisition noise: • • • Noise in receiving coils is complex Gaussian (assuming no post-processing) Noise in x-space related to noise in k-space Final distribution will depend on the reconstruction 11

Noise in MRI 2 - Basic Noise Models 12

Noise in MRI Rician Model X-space (complex) K-space F-1 Complex Gaussian s 2 K Complex Gaussian s 2 n=s 2 K /|W| magnitude |. | Rician s 2 n 13

Noise in MRI Rician Model Complex Magnitude Rician Rayleigh 14 14

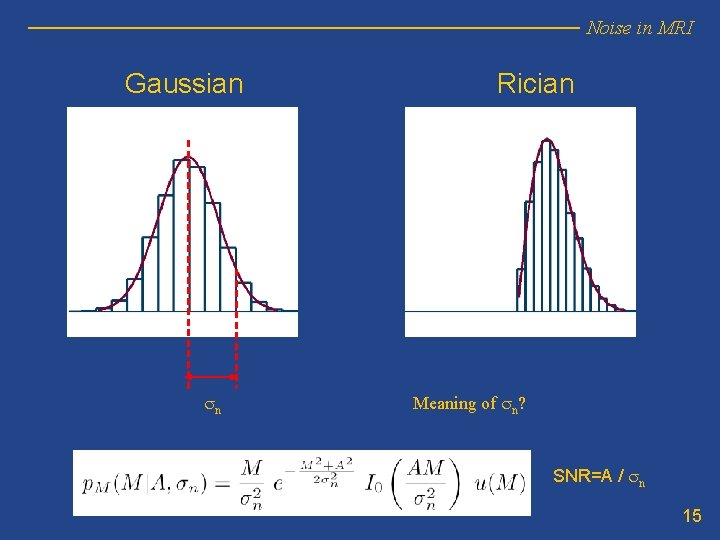
Noise in MRI Gaussian sn Rician Meaning of sn? SNR=A / sn 15

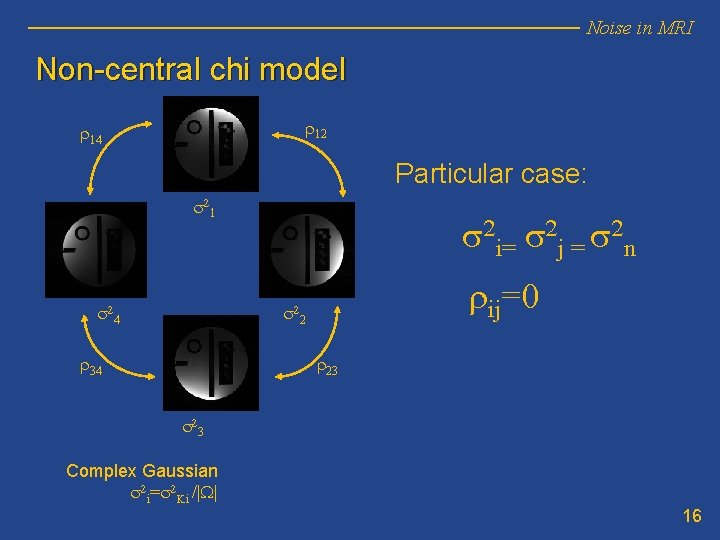
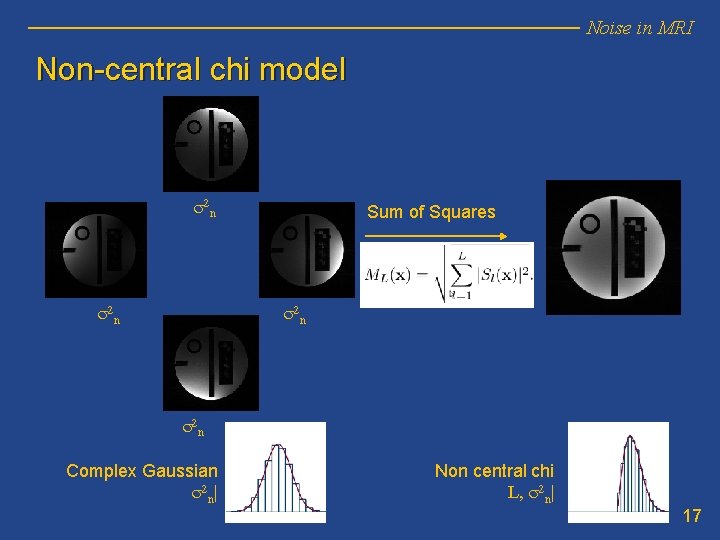
Noise in MRI Non-central chi model r 12 r 14 Particular case: s 2 1 s 2 4 s 2 i= s 2 j = s 2 n rij=0 s 2 2 r 34 r 23 s 2 3 Complex Gaussian s 2 i=s 2 Ki /|W| 16

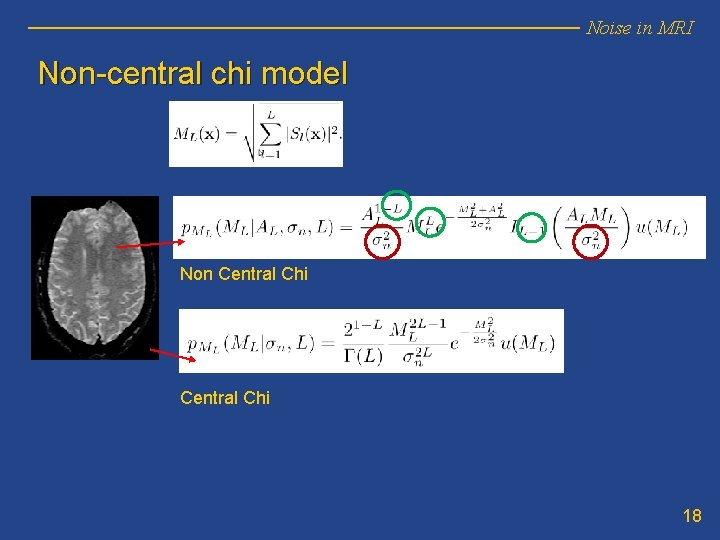
Noise in MRI Non-central chi model s 2 n Sum of Squares s 2 n Complex Gaussian s 2 n | Non central chi L, s 2 n| 17

Noise in MRI Non-central chi model Non Central Chi 18

Noise in MRI Basic models: • • Rician: relation between s 2 n and variance of noise in Gaussian complex data. Nc-chi: also relation between s 2 n and Gaussian Variance. Nc-chi: many times, interesting parameter s 2 n·L E{M(x)2}=A(x)2+2 L·s 2 n SNR=A(x)/L 1/2·sn Usually: equivalence between L·s 2 n (nc-chi) and s 2 n (Rician). 19

Noise in MRI Example: Conventional approach Rician Noncentral-chi 20

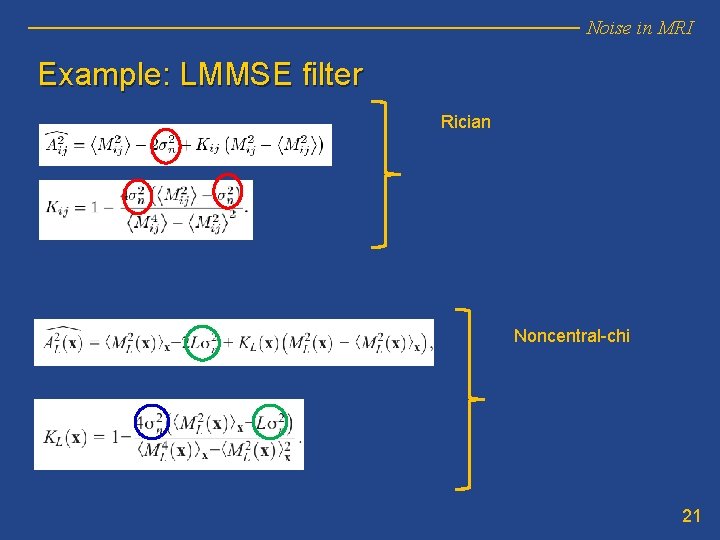
Noise in MRI Example: LMMSE filter Rician Noncentral-chi 21

Noise in MRI 3 - More Complex Models 22

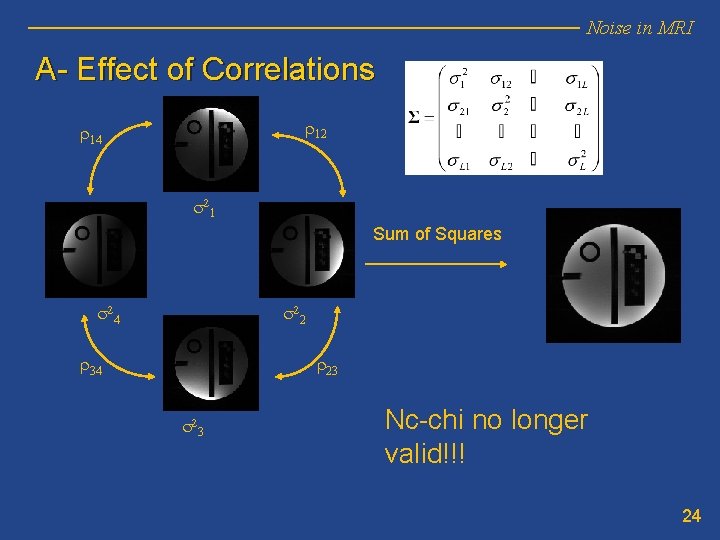
Noise in MRI Limitation of the nc-model: Only valid if: • Same variance of noise in each coil • No correlation between coils • No acceleration • Reconstruction done with sum of squares Real acquisitions. • Correlated, different variances • Accelerated • Reconstructed with different methods 23

Noise in MRI A- Effect of Correlations r 12 r 14 s 2 1 Sum of Squares s 2 4 s 2 2 r 34 r 23 s 2 3 Nc-chi no longer valid!!! 24

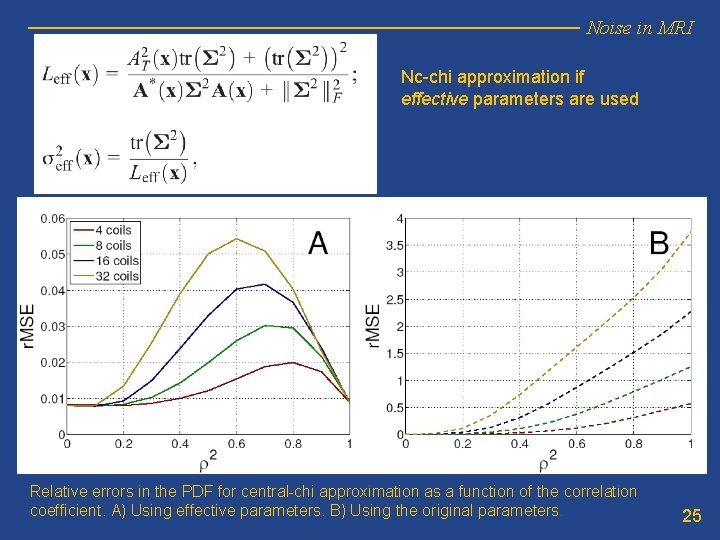
Noise in MRI Nc-chi approximation if effective parameters are used Relative errors in the PDF for central-chi approximation as a function of the correlation coefficient. A) Using effective parameters. B) Using the original parameters. 25

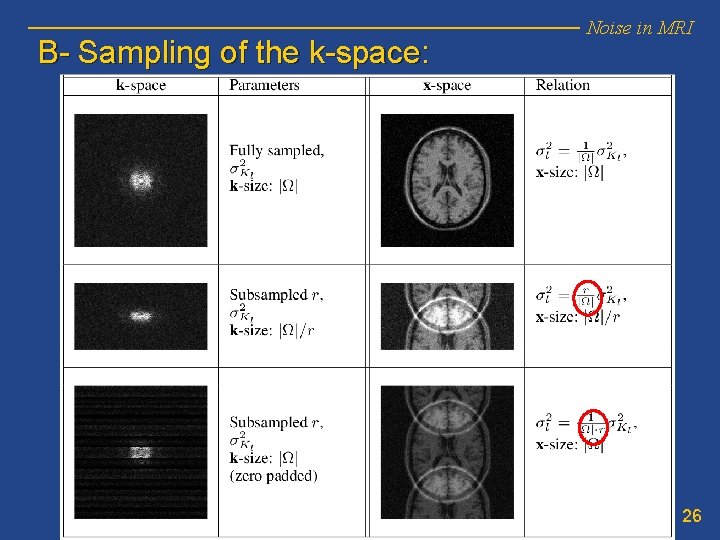
B- Sampling of the k-space: Noise in MRI 26

Noise in MRI In real acquisitions: • • Different variances and correlations → effective values and approximated PDF. Subsampling → modification of s 2 i in x-space Reconstruction method → output may be Rician or an approximation of nc-chi The variance of noise (s 2 i) becomes xdependant → s 2 i(x) 27

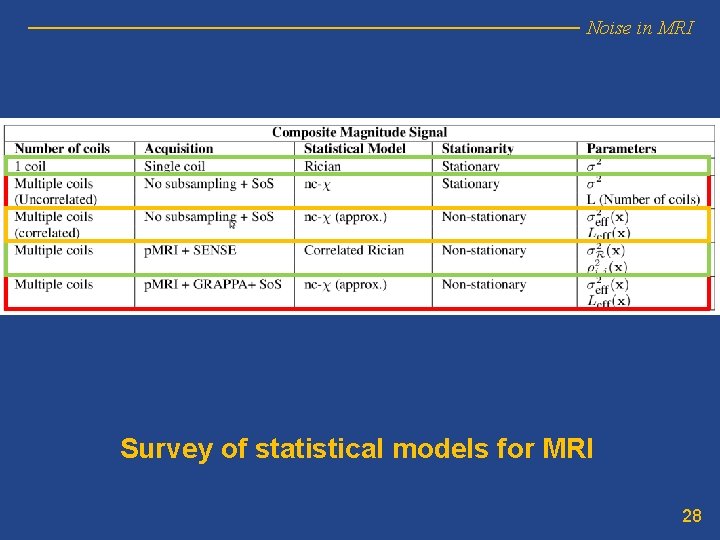
Noise in MRI Survey of statistical models for MRI 28

Noise in MRI 4 - Example: the non stationary nc-chi approximation 29

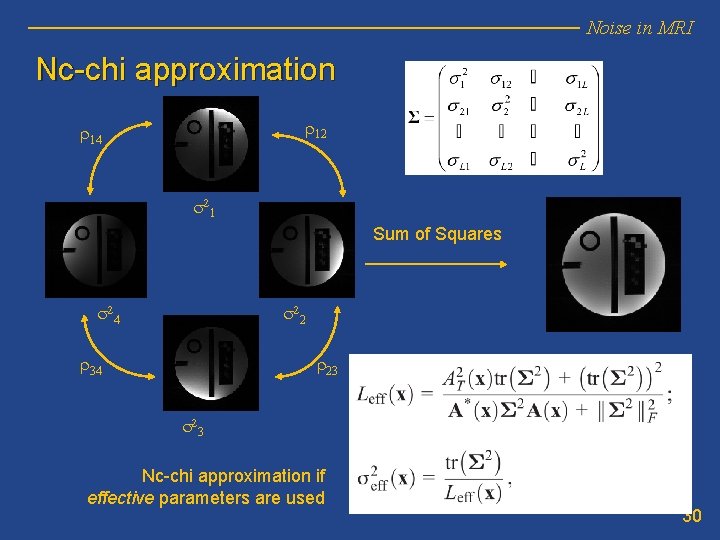
Noise in MRI Nc-chi approximation r 12 r 14 s 2 1 Sum of Squares s 2 4 s 2 2 r 34 r 23 s 2 3 Nc-chi approximation if effective parameters are used 30

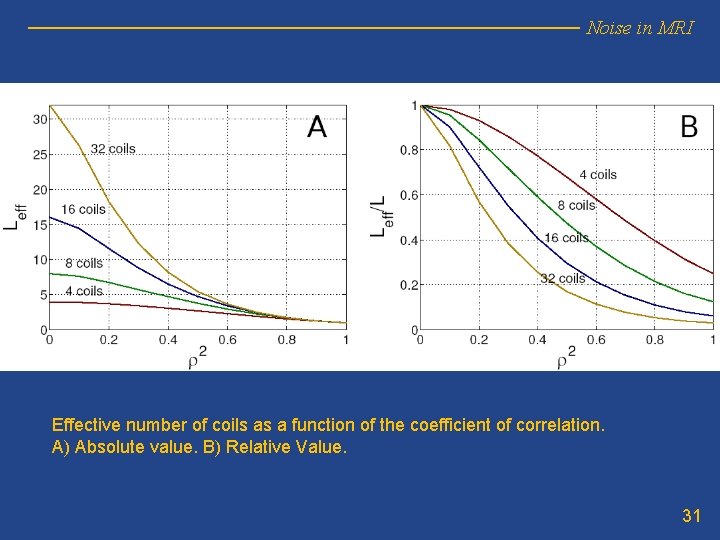
Noise in MRI Effective number of coils as a function of the coefficient of correlation. A) Absolute value. B) Relative Value. 31

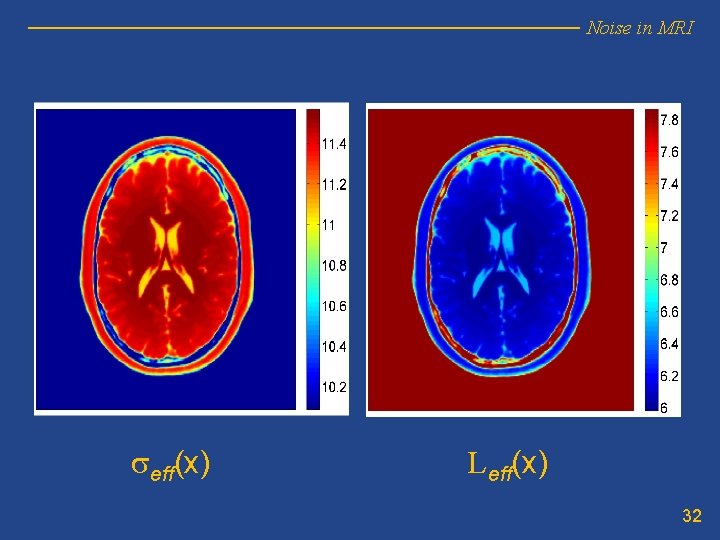
Noise in MRI seff(x) Leff(x) 32

Noise in MRI • Params. seff(x) and Leff(x) both depend on x. • Good news: Leff(x)· s 2 eff(x)= tr(S)=s 21+…+ s 2 L=L·< s 2 i > • The product is a constant: Leff(x)· s 2 eff(x)=L·s 2 n 33

Noise in MRI Implications: • • Equivalence between effective and real parameters Product: easy to estimate Leff(x)· s 2 eff(x)= L·s 2 n=mode{ E{ML 2(x)}x • • }/2 In some problems: only product needed: I 2(x)= E{ML 2(x)}x - 2 L·s 2 n NOTE: If effective values are used for s 2 eff(x), also for Leff(x)· s 2 eff(x)·L → Wrong!!! 34

Noise in MRI Implications: • • My point of view: s 2 eff(x) and Leff(x) should be seen as a single parameter: s 2 L = Leff(x) · s 2 eff(x) and therefore s 2 eff(x) = s 2 L / Leff(x) Some applications do need s 2 eff(x) 35

Noise in MRI X-dependant noise: • Param. s 2 eff(x) now depends on position. • The dependence can be bounded. SNR → 0 s 2 B= s 2 n(1+<r 2>(L-1)) SNR → ∞ s 2 S= s 2 n(1+<r>(L-1)) Total: s 2 eff(x)=(1 -f(x)) s 2 S + f(x) s 2 B with f(x)=(SNR 2(x)+1)-1 36

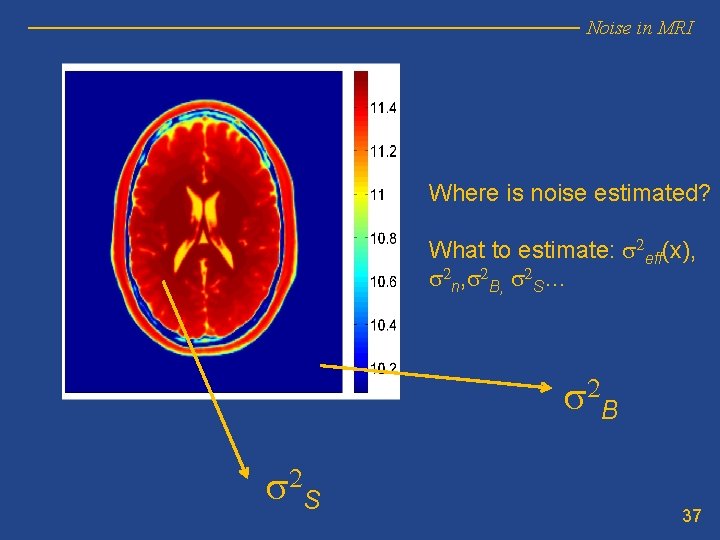
Noise in MRI Where is noise estimated? What to estimate: s 2 eff(x), s 2 n, s 2 B, s 2 S… s 2 B s 2 S 37

Noise in MRI Implications: • • • Estimation over the background → underestimation of noise. Use of a single value of sn → error is most areas. Noise is higher in the high SNR. Main source of non-stationarity: correlation between coils. High correlation: lower effective coils and higher noise. Possible source of error: s 2 eff(x)·L 38

Noise in MRI 5 - Other models 39

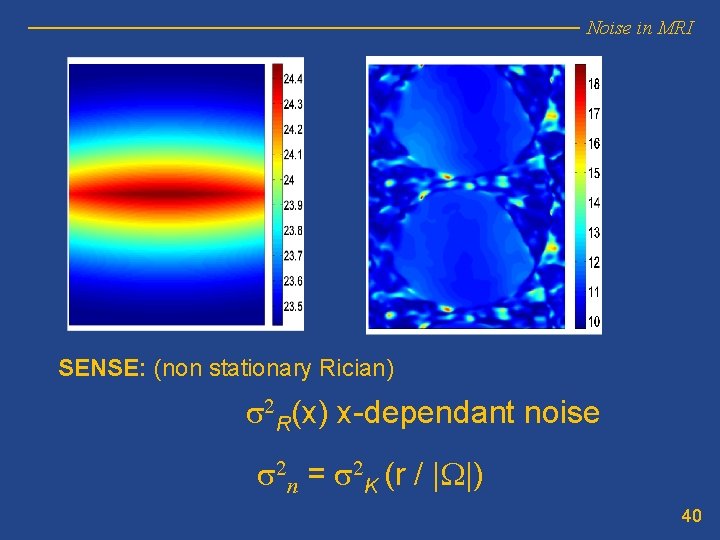
Noise in MRI SENSE: (non stationary Rician) s 2 R(x) x-dependant noise s 2 n = s 2 K (r / |W|) 40

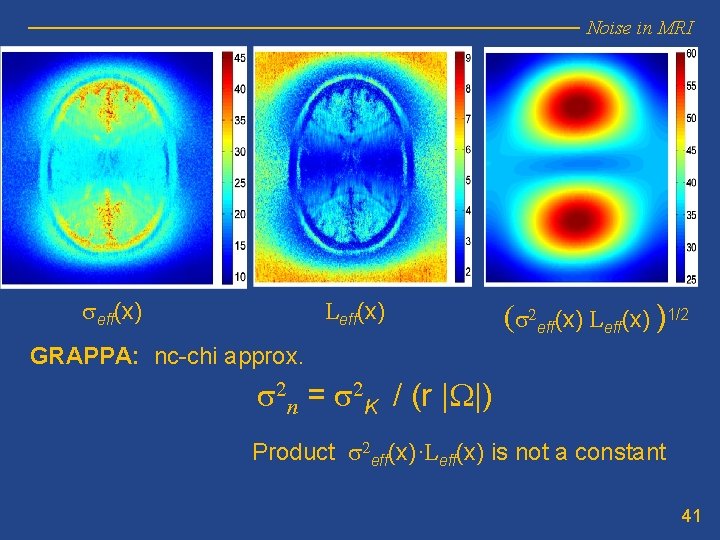
Noise in MRI seff(x) Leff(x) (s 2 eff(x) Leff(x) )1/2 GRAPPA: nc-chi approx. s 2 n = s 2 K / (r |W|) Product s 2 eff(x)·Leff(x) is not a constant 41

Noise in MRI 6 - Conclusions 42

Noise in MRI Conclusions: • • Be sure what you need in your application. Follow the whole reconstruction pipeline to be sure which is your “original” noise. Useful: simplified models to make process easier. Be sure how noise affects the different slides. 43

Noise in MRI Questions? 44

What to measure when measuring noise in MRI Santiago Aja-Fernández sanaja@tel. uva. es Antwerpen 2013