What is z critical value for 80 2

What is z* (critical value) for 80%? 2. What is z* (critical value) for 98%? Estimating a Population Proportion 1. + Warmup

+ Section 8. 2 Estimating a Population Proportion Learning Objectives After this section, you should be able to… ü CONSTRUCT and INTERPRET a confidence interval for a population proportion ü DETERMINE the sample size required to obtain a level C confidence interval for a population proportion with a specified margin of error ü DESCRIBE how the margin of error of a confidence interval changes with the sample size and the level of confidence C

z Interval for a Population Proportion One-Sample z Interval for a Population Proportion Choose an SRS of size n from a large population that contains an unknown proportion p of successes. An approximate level C confidence interval for p is where z* is the critical value for the standard Normal curve with area C between – z* and z*. Use this interval only when the numbers of successes and failures in the sample are both at least 10 and the population is at least 10 times as large as the sample. Estimating a Population Proportion Once we find the critical value z*, our confidence interval for the population proportion p is + n One-Sample

Estimating a Population Proportion After two games of the regular season, Lebron had made 17 of 45 shots attempted. Construct a 95% confidence interval for the proportion of shots that you would expect him to make for the season. + Example #1

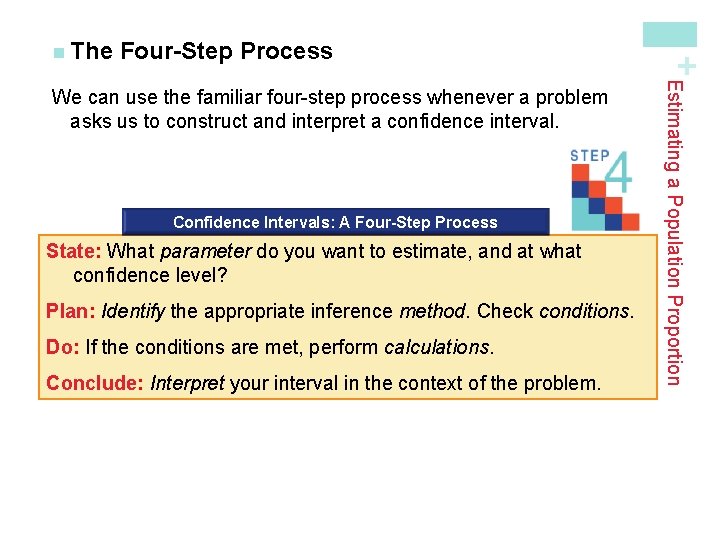
Four-Step Process Confidence Intervals: A Four-Step Process State: What parameter do you want to estimate, and at what confidence level? Plan: Identify the appropriate inference method. Check conditions. Do: If the conditions are met, perform calculations. Conclude: Interpret your interval in the context of the problem. Estimating a Population Proportion We can use the familiar four-step process whenever a problem asks us to construct and interpret a confidence interval. + n The

Estimating a Population Proportion Gallup asked a random sample of 439 U. S. teens whether they thought young people should wait to have sex until marriage. Of the sample, 246 said “Yes”. Construct a 90% confidence interval for the proportion of all teens who would say “Yes” to this question using the 4 -step process. + Example #2

the Sample Size ü z* is the standard Normal critical value for the level of confidence we want. Rearranging the equation from above, the required sample size is: Estimating a Population Proportion In planning a study, we may want to choose a sample size that allows us to estimate a population proportion within a given margin of error. The margin of error (ME) in the confidence interval for p is + n Choosing

#1 Estimating a Population Proportion A customer service manager wants to know the proportion of customers who are satisfied with their dealings with her company. Determine the sample size needed to estimate p within 0. 03 with 95% confidence. + n Example

#2 Estimating a Population Proportion The U. S. Crime Commission wants to estimate p = the proportion of crimes in which firearms are used to within. 02 with 90% confidence. Data from previous years shows that p is about. 6. Find the sample size required to get this margin of error. + n Example