What is work When Work is done by

What is work? • When Work is done by a constant force (constant in both magnitude and direction) and is defined as … – THE PRODUCT OF DISPLACEMENT TIMES THE COMPONENT OF THE FORCE PARRALLEL TO THE DISPLACEMENT • The force and displacement have to be in the same direction or at least parallel. • Examples: – Lifting a book is work. – Holding a book is not.

W=Fxd • measured in Joules (J) • What is a Joule in fundamental units? –J = N * m – J = kg*m/s 2*m – J = kg*m 2/s 2

Pile Driver • A pile driver is a device used to drive stakes into the ground. While building a fence, Adam drops a pile driver through a vertical distance of 8 m. How much Work is done if he uses a force of 5 x 106 N?

What is work? • Consider the equation W = F cos Θ in regards to displacement (Fd cos Θ): • F is the force • d is the net displacement of the object • Θ is the angle between the directions of the force and net displacement • What does this say when Θ = 0, Θ = 90, Θ = 180 in regards to displacement • “-” ? ? ? • Example – Pushing a broom or pulling a box

Work Example A sled, which has a mass of 45. 0 kg. , is sitting on a horizontal surface. A force of 120 N is applied to a rope attached to the front of the sled such that the angle between the front of the sled and the horizontal is 35º. As a result of the application of this force the sled is pulled a distance of 500 meters at a relatively constant speed. How much work was done to this sled by the applied force?

Work Example A 75 kg crate is moved across a floor, against friction, at a constant speed. It moves a distance of 41 m, and 18 k. J of work is done on it. What is the coefficient of friction?

Example Big Joe pulls a 300 N sled across level snow with a force of 520 N along a rope that is q above the horizontal. If the sled moves a distance of 60 m, and Joe does 20 k. J of work, what is q?

What is power? • Power is the rate at which work is done. • P = W/t • P = Fd/t • Can two people do the same amount of work on an object but have different amounts of power? – yes, how? • time

The Watt • power is measured in watts (W) • What is a watt in fundamental units? – W = J/s – W = kg*m 2/s 3

Pile Driver Power? • If Adam finishes the project in 60 seconds, How much Power was generated? Can you build a fence in 60 seconds?

Energy • is defined as the ability to do work. • So, if something has energy it has the ability to do work. – That is it can displace an object with a force. • To change the amount of energy an object has you must do work on the object.

Ex • When you draw back a bow you do work on the bow. – The bow now has energy and can do work on the arrow. • When you lift a hammer you do work on the hammer. – the hammer now has energy and can do work on the nail

Types of energy • potential, kinetic, solar, electrical, nuclear, chemical etc. • Mechanical energy is broken down into two types – Potential energy – Kinetic energy

Kinetic energy • what does kinetic mean? – motion • energy of motion – so things that are moving have energy • What would affect how much energy a moving object has? – m, v • KE = ½ mv 2

Work Energy Theorem vf 2 = vi 2 + 2 ad W = Fd W=mad a = vf 2 – vi 2 2 d W = m vf 2 –vi 2 d 2 d W = ½m(vf 2 –vi 2) W = ½mvf 2 – ½mvi 2 or W = DKE

Potential energy • stored energy • energy of position – drawn bow, compressed spring, rubber band • when position means height – we have gravitational potential energy

Gravitational PE • PE = mgh • How does an object get that energy? – work was done on the object – W=mgh – Fd=mgh – mad = mgh

Conservation of energy • Law of conservation of energy – Energy cannot be created or destroyed. • Then where does it go? – Transferred

Conserving energy • In a closed system the initial energy is equal to the final energy. • or there is no net gain or loss of energy at any point in a closed system. • or if you start with 1000 J of energy at any point in the system the energy is 1000 J


What type of energy does the ball have at this point?

How does this look conceptually in a problem? • The energy of the ball is constant during the vertical loop demonstration. • At the top of the ramp it has 0 velocity so, no KE – It has height so it has PE – So the initial energy of the ball is equal to the PE at the top of the ramp

• At any other point during the demonstration the energy will be equal to the PE at the beginning of the demonstration. • The energy at the bottom of the loop is equal to that at the top of the loop – but is all converted to KE – the ball is moving and has 0 height

• At the top of the loop the ball has the same energy it had at the top of the ramp. – It is made up of PE and KE – the ball is moving and has height

Solving the problem Ei = E f PEi + KEi = PEf + KEf mghi + ½ mvi 2 = mghf + ½ mvf 2
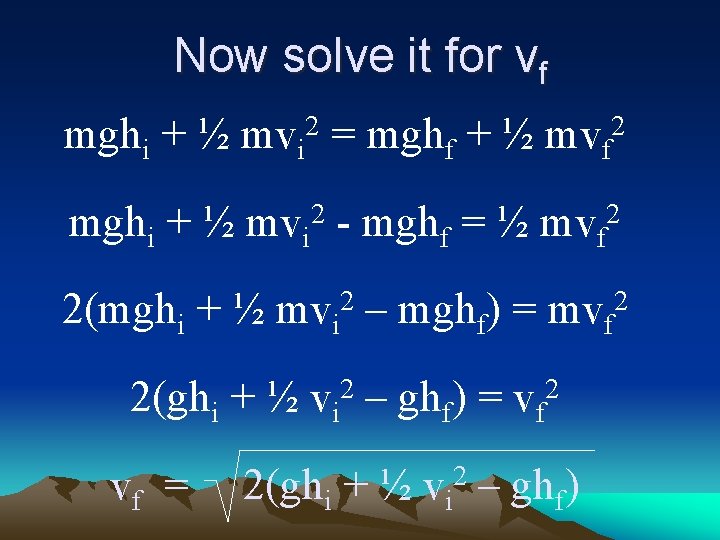
Now solve it for vf mghi + ½ 2 mvi = mghf + ½ mvf 2 mghi + ½ mvi 2 - mghf = ½ mvf 2 2(mghi + ½ mvi 2 – mghf) = mvf 2 2(ghi + ½ vi 2 – ghf) = vf 2 vf = 2(ghi + ½ vi 2 – ghf)

Machines • : device that helps do work by changing the magnitude or direction of applied force • Why do we use machines? – To make work EASIER • Machines do not change the amount of work done!!! • So what does EASIER mean?

Wi = W o • Easier means less force has to be used. • therefore that force has to be applied over a larger distance Winput = Woutput Fi di = Fo do
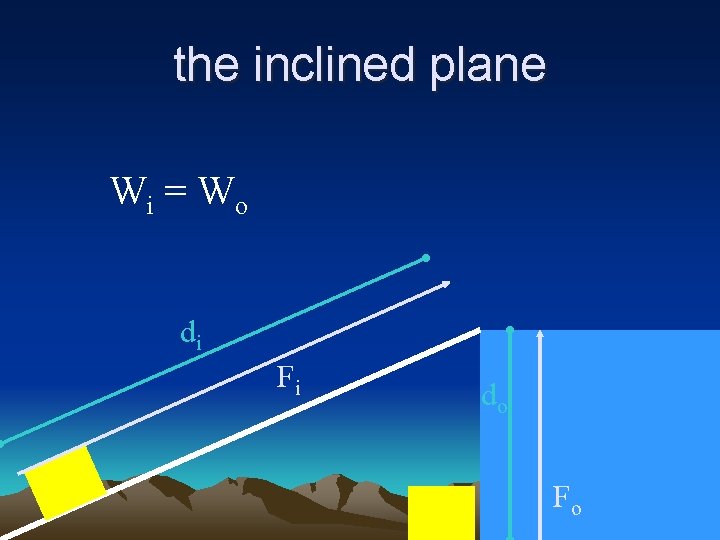
the inclined plane Wi = W o di Fi do Fo
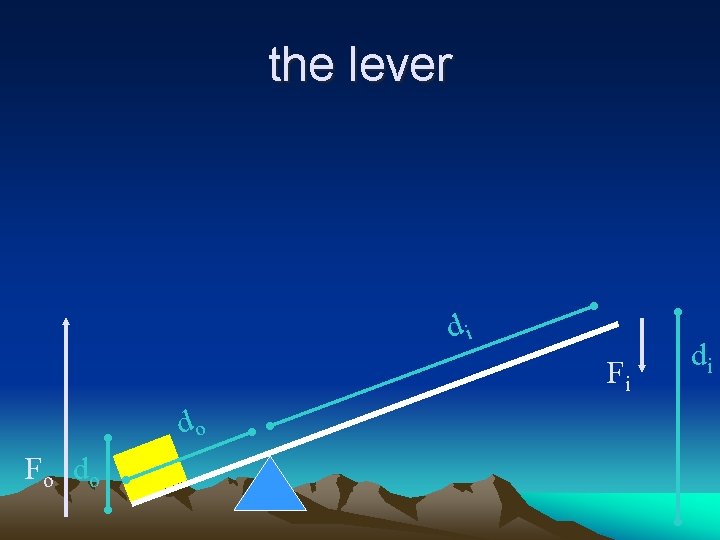
the lever di Fi do Fo do di

How much do machines help us? • we measure this with ideal and actual mechanical advantage IMA = di do F AMA = o Fi

Key Terms – Mechanical Advantage • Force Out = Resistance • Force In = Effort • Distance In = Effort Distance • Distance Out = Resistance Distance

How well do machines work? • we measure this with efficiency Efficiency = Wo Wi AMA = IMA x 100 = %
- Slides: 33