What is Trigonometry The word trigonometry means Measurement

What is Trigonometry? The word trigonometry means “Measurement of Triangles” • The study of properties and functions involved in solving triangles. • Relationships among sides and angles of triangles • Phenomena that occur in cycles and/or waves, rotations & vibrations APPLICATIONS Astronomy Planetary Orbits Navigation Light Rays Surveying Sound Waves DNA Research

1. 1 Review: Lines, Segments, Rays, Angles B Line 2 distinct points A and B determine a line. A AB Line AB Segment or Line Segment – the portion of the line between A and B A AB Segment AB B Ray – part of a line consisting of 1 endpoint , A, and all the points of the line on 1 side of the endpoint. -- in other words, the portion of line AB that starts at A & continues through B and on past B, is called Ray AB. A B AB Ray AB Angle – 2 rays or 2 line segments with a common endpoint. The rays are the sides of the angle & the common endpoint is the vertex. A 2 < AFP or <PFA or <F or <2 F

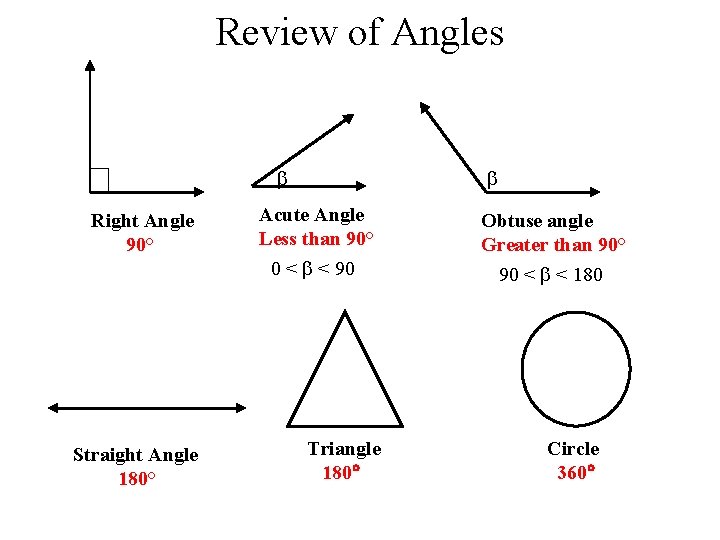
Review of Angles Right Angle 90° Straight Angle 180° Acute Angle Less than 90° 0 < < 90 Triangle 180 Obtuse angle Greater than 90° 90 < < 180 Circle 360

Special Angle Relationships Supplementary Angles – Two angles whose sum is 180° 2 1 < 1 and <2 are supplementary (Remember: A straight angle (line) measures 180°) Complementary Angles – Two angles whose sum is 90° <1 and <2 are complementary 1 2 Note: Angles do not have to be adjacent to be supplementary or complementary.

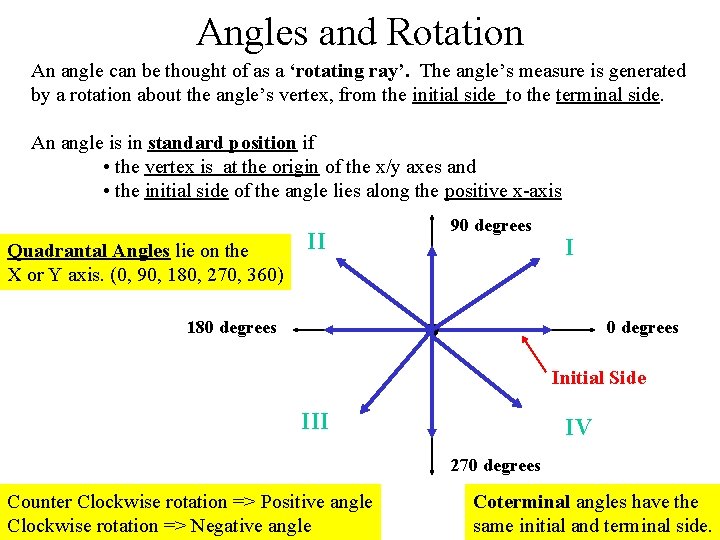
Angles and Rotation An angle can be thought of as a ‘rotating ray’. The angle’s measure is generated by a rotation about the angle’s vertex, from the initial side to the terminal side. An angle is in standard position if • the vertex is at the origin of the x/y axes and • the initial side of the angle lies along the positive x-axis Quadrantal Angles lie on the X or Y axis. (0, 90, 180, 270, 360) II 90 degrees I 180 degrees Initial Side III IV 270 degrees Counter Clockwise rotation => Positive angle Clockwise rotation => Negative angle Coterminal angles have the same initial and terminal side.

Angle Measures Angles are measured in degrees. (Angles are also measured in Radians which we will discuss later) One complete rotation of a ray (forming an angle) is 360º Minutes and Seconds measure portions of a degree. 1’ (1 Minute) = 1/60 of a degree 1” (1 Second) = 1/60 of a minute An angle might measure: 12º 42´ 38´´ Convert to degrees only 38/60 =. 6333 => 12º 42. 6333’ 42. 6333/60 => 12. 710555º Convert back to degrees/minutes/seconds. 710555 X 60 = 42. 6333 => 12º 42. 6333’. 6333 x 60 = 37. 998 => 12º 42´ 38´´

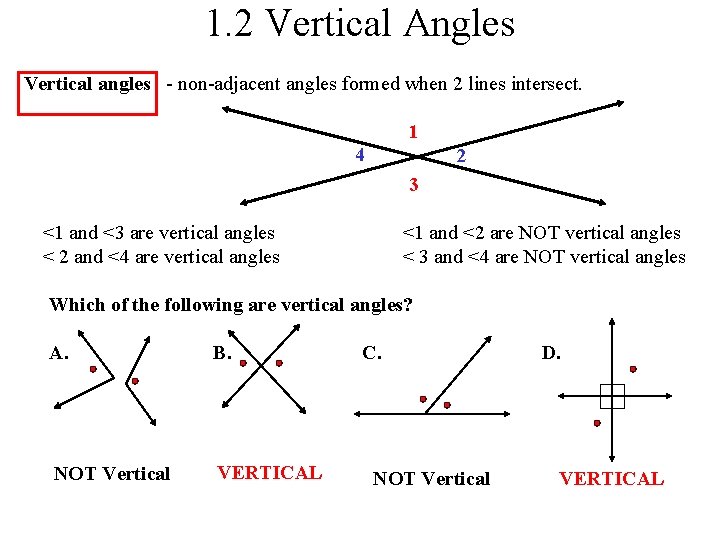
1. 2 Vertical Angles Vertical angles - non-adjacent angles formed when 2 lines intersect. 1 4 2 3 <1 and <3 are vertical angles < 2 and <4 are vertical angles <1 and <2 are NOT vertical angles < 3 and <4 are NOT vertical angles Which of the following are vertical angles? A. B. NOT Vertical VERTICAL C. NOT Vertical D. VERTICAL

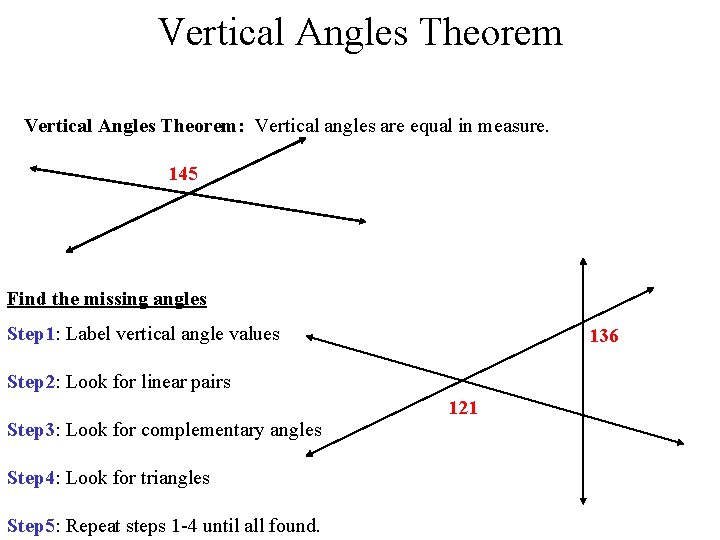
Vertical Angles Theorem: Vertical angles are equal in measure. 145 Find the missing angles Step 1: Label vertical angle values 136 Step 2: Look for linear pairs Step 3: Look for complementary angles Step 4: Look for triangles Step 5: Repeat steps 1 -4 until all found. 121

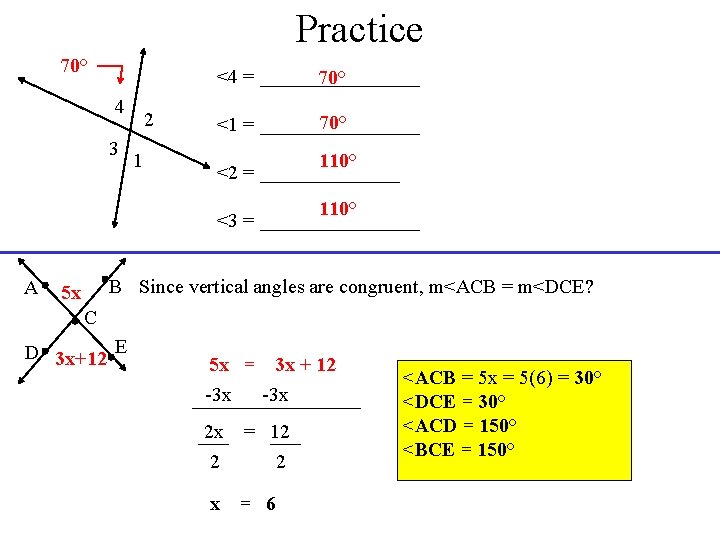
Practice 70° <4 = ________ 70° 4 3 2 1 70° <1 = ________ 110° <2 = _______ 110° <3 = ________ A B Since vertical angles are congruent, m<ACB = m<DCE? 5 x C D 3 x+12 E 5 x = 3 x + 12 -3 x 2 x 2 = 12 2 x = 6 <ACB = 5 x = 5(6) = 30° <DCE = 30° <ACD = 150° <BCE = 150°

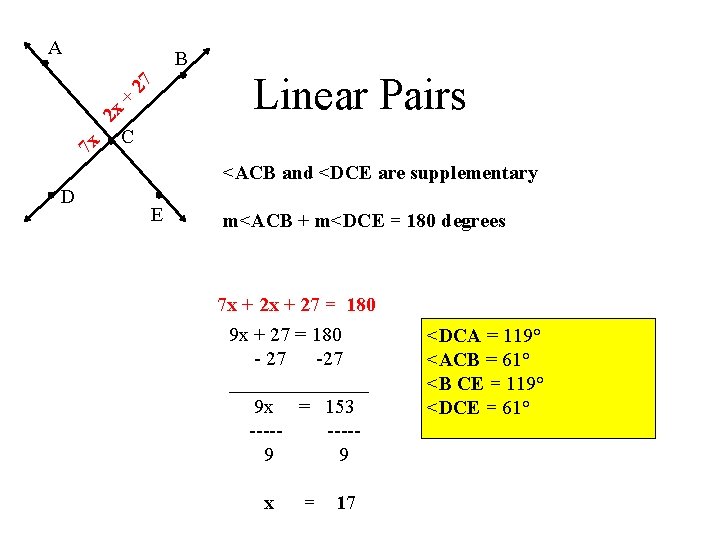
A B 7 x 2 x + 27 Linear Pairs C <ACB and <DCE are supplementary D E m<ACB + m<DCE = 180 degrees 7 x + 27 = 180 9 x + 27 = 180 - 27 -27 _______ 9 x = 153 ----9 9 x = 17 <DCA = 119° <ACB = 61° <B CE = 119° <DCE = 61°

Recall From Geometry: Parallel Lines Cut by a Transversal 2 1 4 3 6 5 8 7 If two parallel lines are cut by a transversal then • Corresponding angles are congruent. (Ex: <2 and <6) • • Alternate interior angles are congruent (Ex: <3 and <5) Alternate exterior angles are congruent (Ex: <1 and <7) • • Same side interior angles are supplementary (Ex: <3 and <6) Same side exterior angles are supplementary (Ex: <2 and <7)

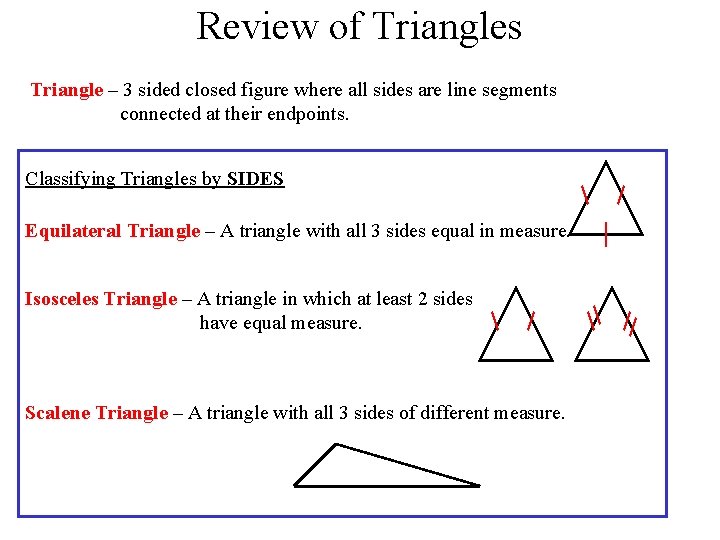
Review of Triangles Triangle – 3 sided closed figure where all sides are line segments connected at their endpoints. Classifying Triangles by SIDES Equilateral Triangle – A triangle with all 3 sides equal in measure. Isosceles Triangle – A triangle in which at least 2 sides have equal measure. Scalene Triangle – A triangle with all 3 sides of different measure.

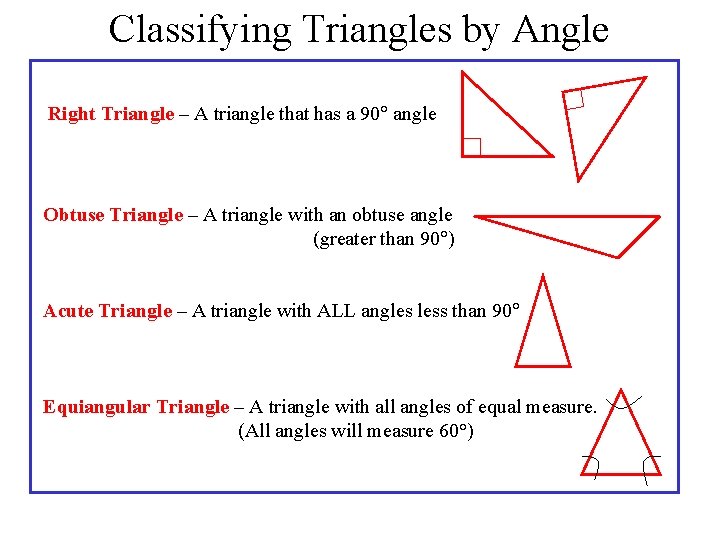
Classifying Triangles by Angle Right Triangle – A triangle that has a 90 angle Obtuse Triangle – A triangle with an obtuse angle (greater than 90 ) Acute Triangle – A triangle with ALL angles less than 90 Equiangular Triangle – A triangle with all angles of equal measure. (All angles will measure 60°)

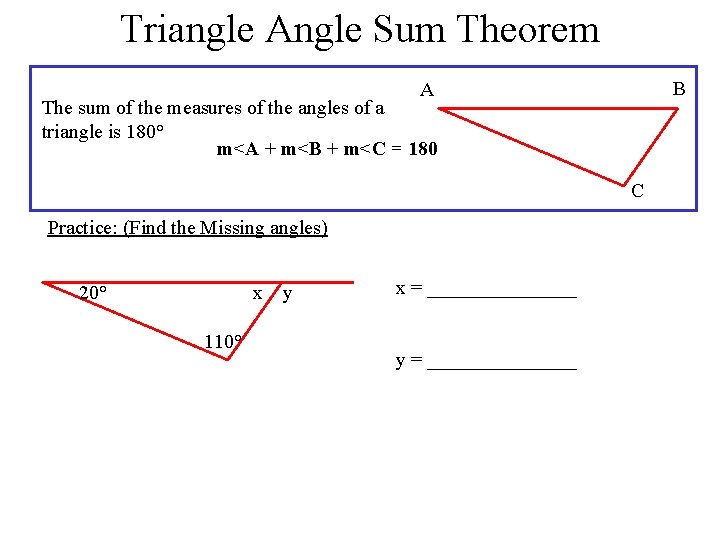
Triangle Angle Sum Theorem B A The sum of the measures of the angles of a triangle is 180° m<A + m<B + m<C = 180 C Practice: (Find the Missing angles) 20° x 110° y x = ________ y = ________

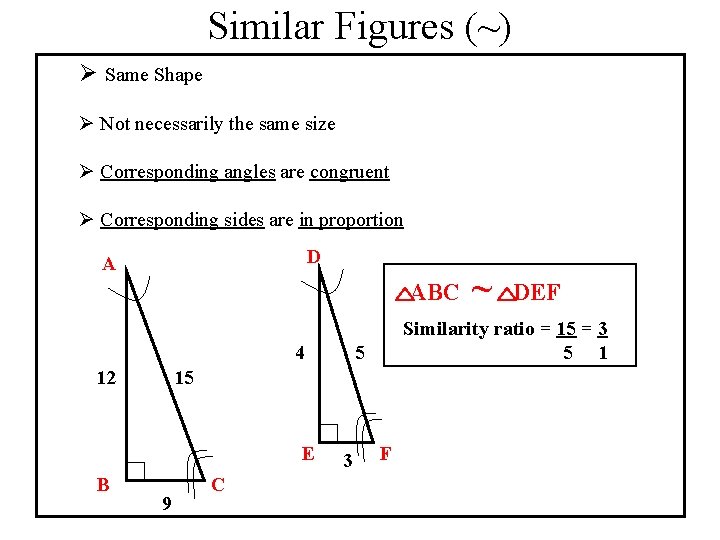
Similar Figures (~) Ø Same Shape Ø Not necessarily the same size Ø Corresponding angles are congruent Ø Corresponding sides are in proportion D A ABC 4 12 B 5 9 C 3 DEF Similarity ratio = 15 = 3 5 1 15 E ~ F

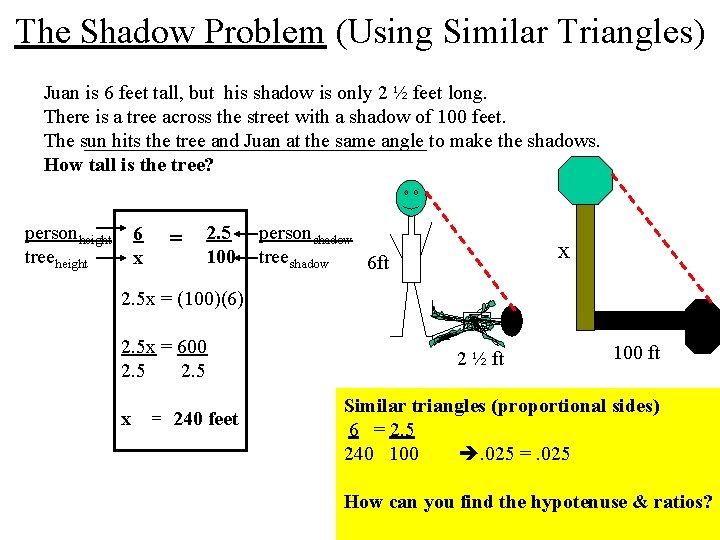
The Shadow Problem (Using Similar Triangles) Juan is 6 feet tall, but his shadow is only 2 ½ feet long. There is a tree across the street with a shadow of 100 feet. The sun hits the tree and Juan at the same angle to make the shadows. How tall is the tree? personheight treeheight 6 x = 2. 5 100 personshadow treeshadow 6 ft x 2. 5 x = (100)(6) 2. 5 x = 600 2. 5 x = 240 feet 2 ½ ft 100 ft Similar triangles (proportional sides) 6 = 2. 5 240 100 . 025 =. 025 How can you find the hypotenuse & ratios?

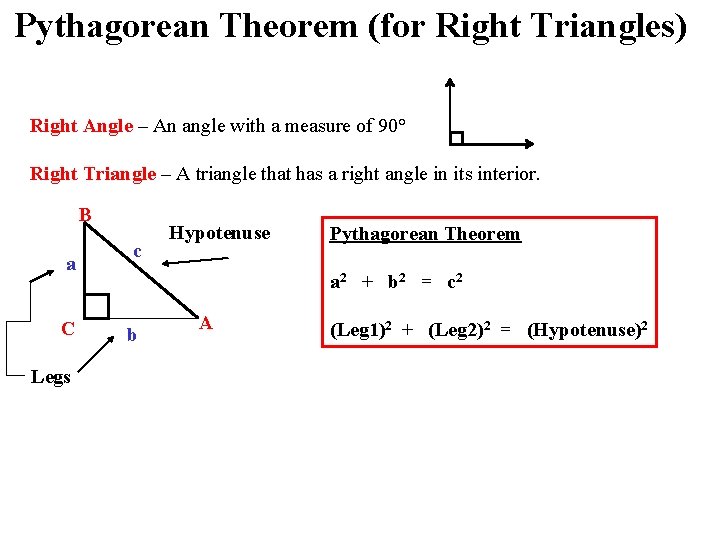
Pythagorean Theorem (for Right Triangles) Right Angle – An angle with a measure of 90° Right Triangle – A triangle that has a right angle in its interior. B a C Legs c Hypotenuse Pythagorean Theorem a 2 + b 2 = c 2 b A (Leg 1)2 + (Leg 2)2 = (Hypotenuse)2

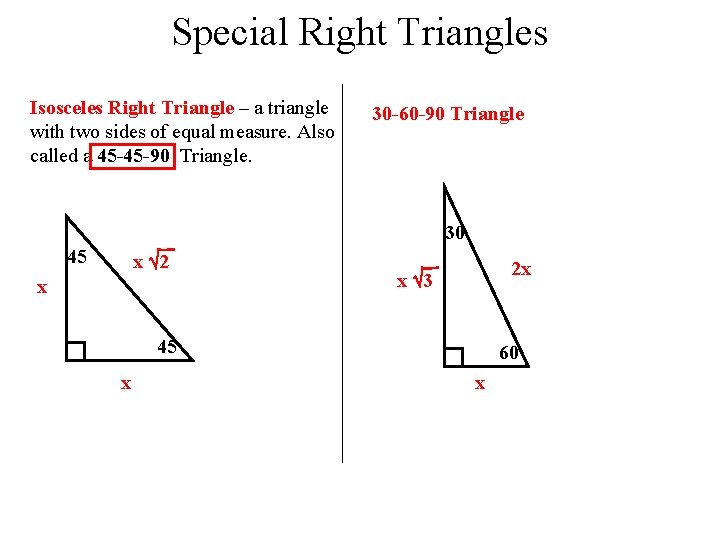
Special Right Triangles Isosceles Right Triangle – a triangle with two sides of equal measure. Also called a 45 -45 -90 Triangle. 30 -60 -90 Triangle 30 45 x 2 x x 3 45 x 60 x

1. 3/2. 1 Six Trig Functions for Right Triangles sin ( ) = Opposite csc ( ) = Hypotenuse Opposite cos ( ) = Adjacent sec ( ) = Hypotenuse [secant] Adjacent tan ( ) = Opposite cot( ) = Adjacent Opposite Note: is an Acute angle. 12 [cosecant] 13 5 [cotangent] sin ( ) = 12 13 csc( ) = 13 12 cos( ) = 5 13 sec( ) = 13 5 tan( ) = 12 / 5 cot( ) = 5 / 12

Trig Functions - Any Angle - Any Quadrant 90 degrees P(x, y) r 180 degrees Quadrant II sin( ) = opposite/hypotenuse = y/r cos( ) =adjacent/hypotenuse = -x/r tan( ) = opposite/adjacent = y/(-x) Quadrant III sin( ) = opposite/hypotenuse = -y/r cos( ) =adjacent/hypotenuse = -x/r tan( ) = opposite/adjacent = (-y)/(-x) x y 0 degrees Quadrant I sin( ) = opposite/hypotenuse = y/r 270 degrees cos( ) =adjacent/hypotenuse = x/r tan( ) = opposite/adjacent = y/x Quadrant IV sin( ) = opposite/hypotenuse = -y/r cos( ) =adjacent/hypotenuse = x/r tan( ) = opposite/adjacent = (-y)/x

Trig Functions of Quadrantal Angles P(0, y) 90 degrees 180 degrees P(-x, 0) P(0, -y) 270 degrees sin(90) = y/r = y/y = 1 cos(90) = 0/r = 0 tan(90) = y/0 = Undefined sin (0) = 0/r = 0 cos (0) = x/r = x/x = 1 tan (0) = 0/x = 0 sin (270) = -y/r = -y/y = -1 sin(180) = 0/r = 0 cos (270) = 0/r = 0 cos(180) = -x/r = -x/x = -1 tan (270) = -y/0 = Undefined tan(180) = 0/(-x) = 0 (See Page 27 for a Complete list for all 6 trigonometric functions. )

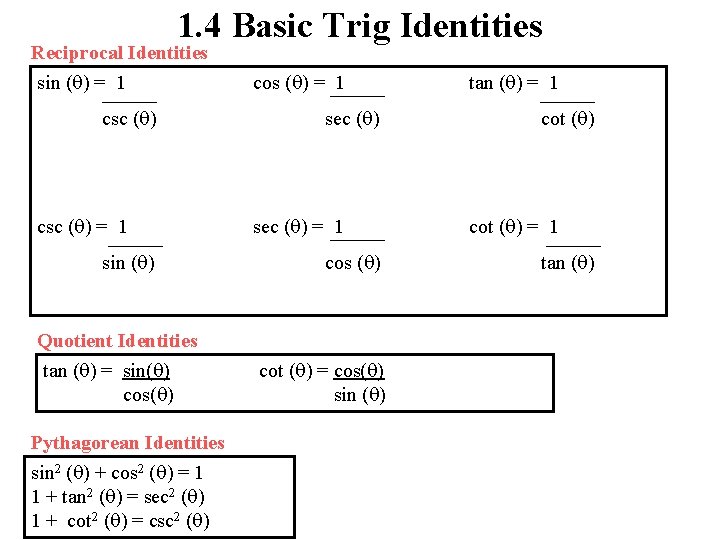
1. 4 Basic Trig Identities Reciprocal Identities sin ( ) = 1 csc ( ) = 1 sin ( ) Quotient Identities tan ( ) = sin( ) cos( ) Pythagorean Identities sin 2 ( ) + cos 2 ( ) = 1 1 + tan 2 ( ) = sec 2 ( ) 1 + cot 2 ( ) = csc 2 ( ) cos ( ) = 1 sec ( ) = 1 cos ( ) cot ( ) = cos( ) sin ( ) tan ( ) = 1 cot ( ) = 1 tan ( )