What is Trigonometry and where is it used

What is Trigonometry and where is it used in real life? • Trigonometry traditionally means the “measurement of triangles” – Relationships among sides and angles of triangles – Used in development of astronomy, navigation, and surveying • With development of Calculus and physical sciences in 17 th century, a different perspective arose – people began to view trigonometric relationships as functions. – Applications include physical phenomena including rotations and vibrations, sound waves, light rays, planetary orbits, vibrating strings, pendulums, orbits of atomic particles, etc…

Lesson 4. 1 Trigonometrey: Angles

What is an angle? An angle is determined by rotating a ray (half-line) about its endpoint. The measure of an angle is determined by the amount of rotation from the initial side (starting position) to the terminal side (ending position) An angle is in standard position when the vertex is at the origin and the initial side coincides with the positive x-axis A positive angle has a counterclockwise rotation A negative angle has a clockwise rotation

What are some other definitions I need to remember from geometry? • Supplementary angles are two angles that add up to 180ᴼ • Complementary angles are two angles that add up to 90ᴼ

Reviewing names of Angles…

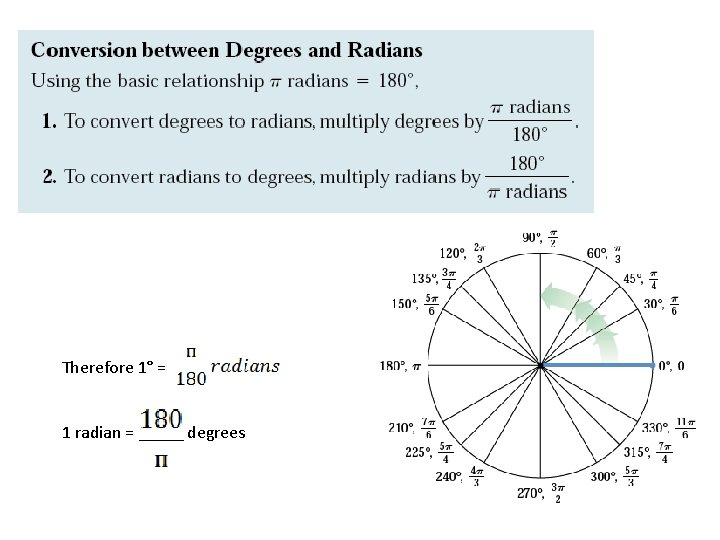
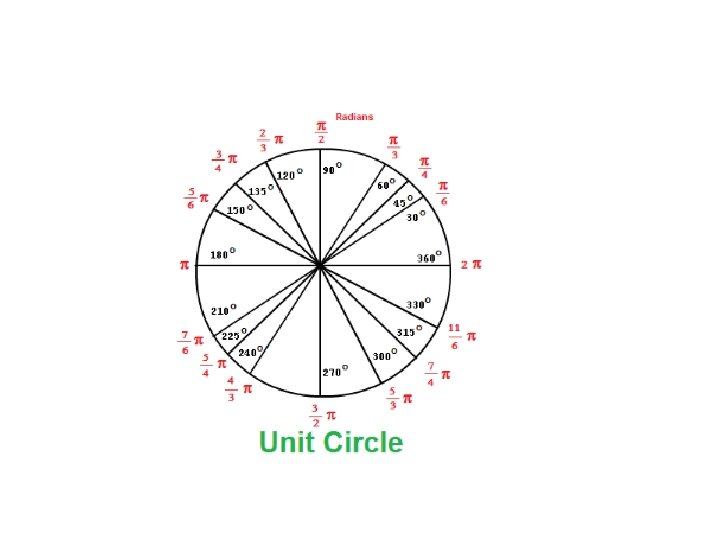
There are two ways of measuring angles • Degrees • Radians

Degree Measure • A full revolution (counterclockwise) around circle corresponds to 360ᴼ degrees. • A half rotation is 180ᴼ

What is Radian Measure? One radian is the measure of a central angle such that the length of the intercepted arc is the same length as the radius. Wh Because the circumference of a circle is C = 2πr, The arc length of one full rotation is S = 2πr e and re r = r s= arc adius len gth =s Ɵ

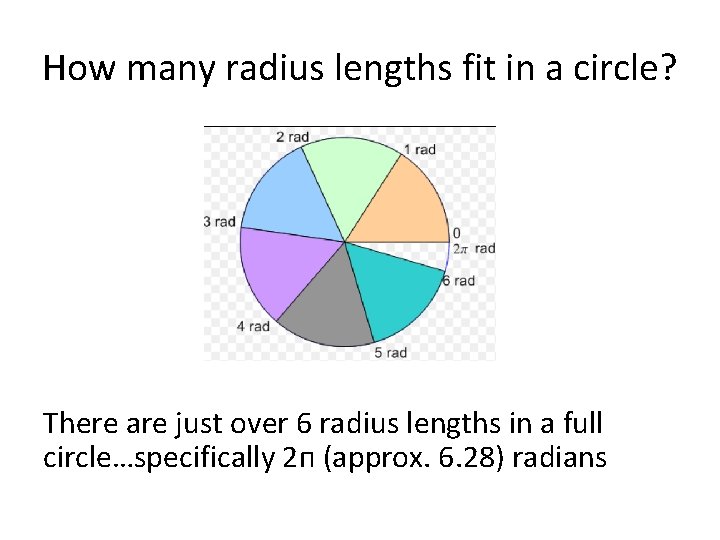
How many radius lengths fit in a circle? There are just over 6 radius lengths in a full circle…specifically 2 п (approx. 6. 28) radians

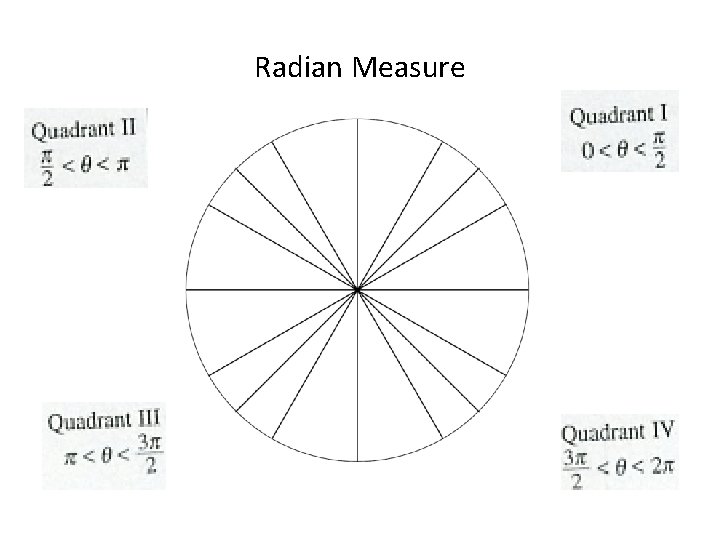
Radian Measure

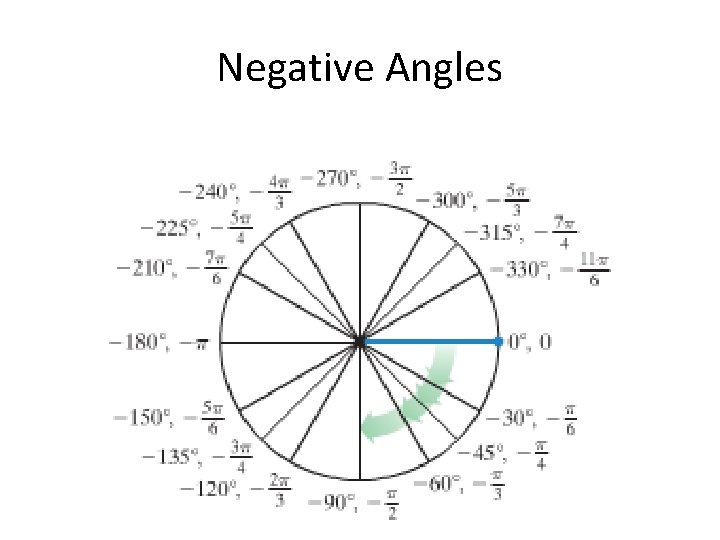
Negative Angles

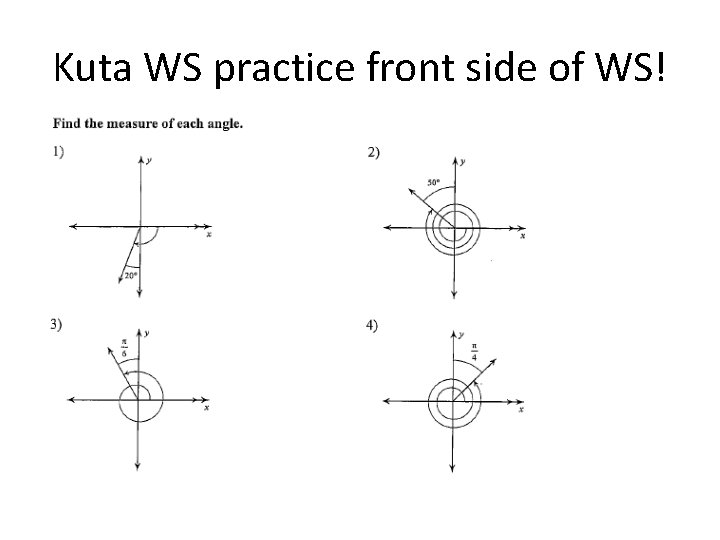
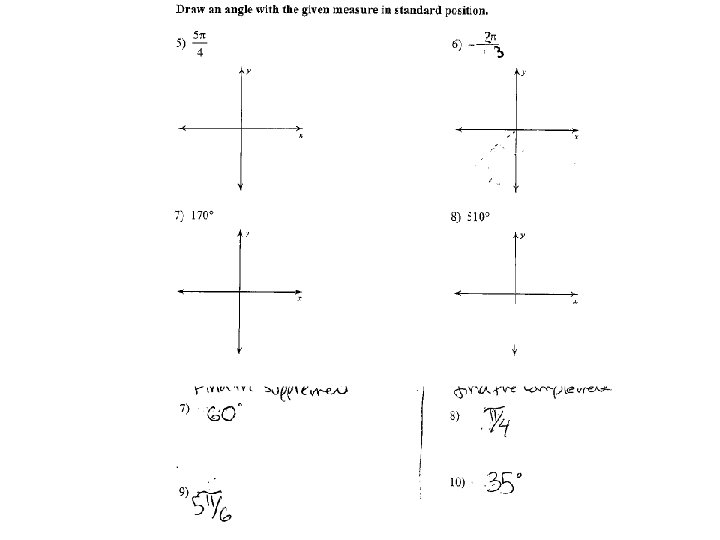
Kuta WS practice front side of WS!

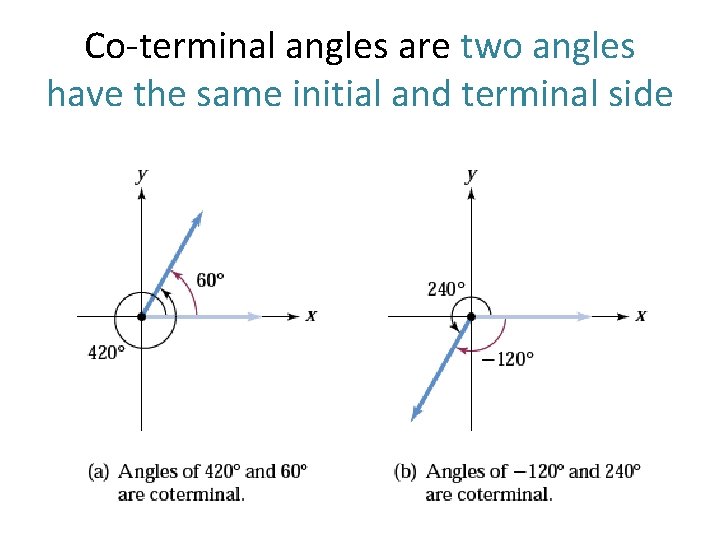
Co-terminal angles are two angles have the same initial and terminal side

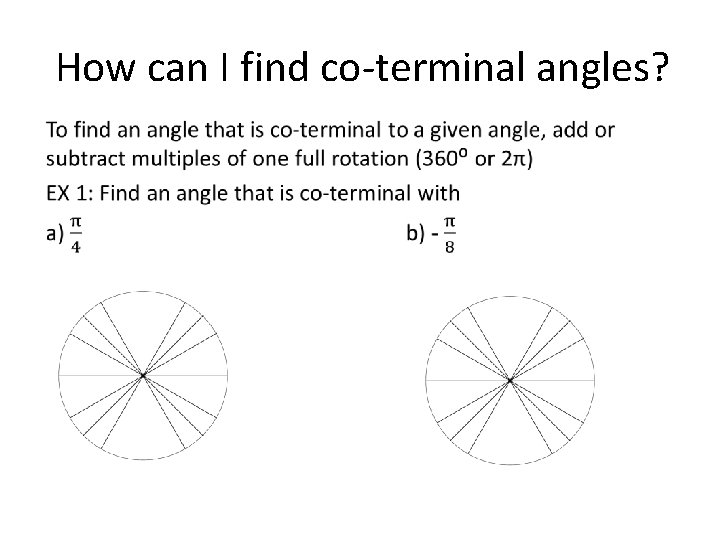
How can I find co-terminal angles? •

You Try! •

Warm Up to PII Describe in WORDS how would you convert 24 feet to inches. Then do the conversion. Show all work.

Therefore 1° = 1 radian = degrees

EX 1 a) Convert 120ᴼ to radians •

HW 4. 1 A Pg 265 #3 -8 all, 11 -13 all, 15 -18 all, 23, 27 -30 all

You Try!

EX 2 : Convert angle measure to decimal degree form 5° 40’ 12’’ You Try! 34° 30’ 36’’

What is Linear and Angular Speed? • Time usually in seconds

EX 3: A circle has a radius of 4 inches. Find the length of the arc intercepted by a central angle of 240°, as shown in the picture. Solution:

You Try! Find the radian measure of the central angle of a circle of radius 22 feet and an arc length of 10 feet.

EX 4: The second hand of a clock is 10. 2 cm long, as shown in the figure. Find the linear speed of the tip of this second hand. In our formula for linear speed, we have Step 1: Find the arc length using circumference formula since we’re not given an angle. S = C = 2πr Step 2: Find our time. Since this is a clock, the hand will take 60 seconds to rotate Step 3: Pop into formula

EX 5: Finding angular speed

You Try! a) The second hand of a clock is 8 cm long. Find the linear speed of the tip of the second hand as it passes around the clock face. b) The circular blade on a saw rotates at 24 rev/min. Find the angular speed in radians/sec.

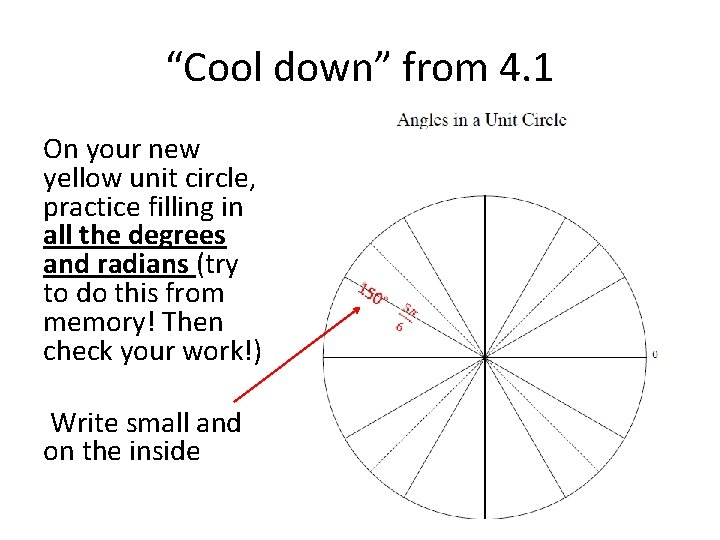
“Cool down” from 4. 1 On your new yellow unit circle, practice filling in all the degrees and radians (try to do this from memory! Then check your work!) Write small and on the inside

HW 4. 1 B Pg 266 #31, 32, 35, 36, 47 -61 odd, 71, 72, 7783 odd, 96, 97