What is the most realistic singlecompartment neuron model

What is the most realistic single-compartment neuron model? Romain Brette romain. brette@inserm. fr

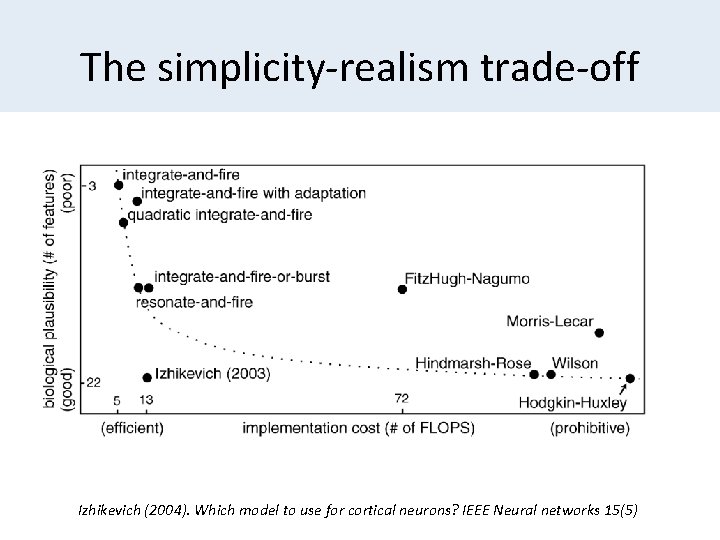
The simplicity-realism trade-off Izhikevich (2004). Which model to use for cortical neurons? IEEE Neural networks 15(5)

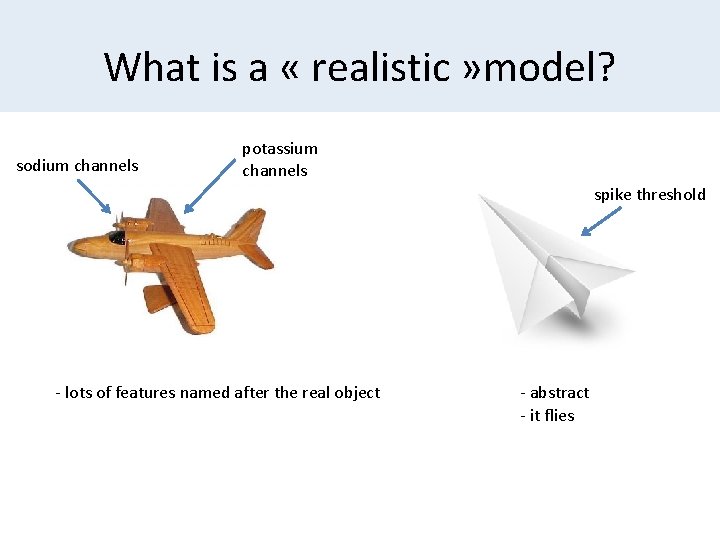
What is a « realistic » model? sodium channels potassium channels spike threshold - lots of features named after the real object - abstract - it flies

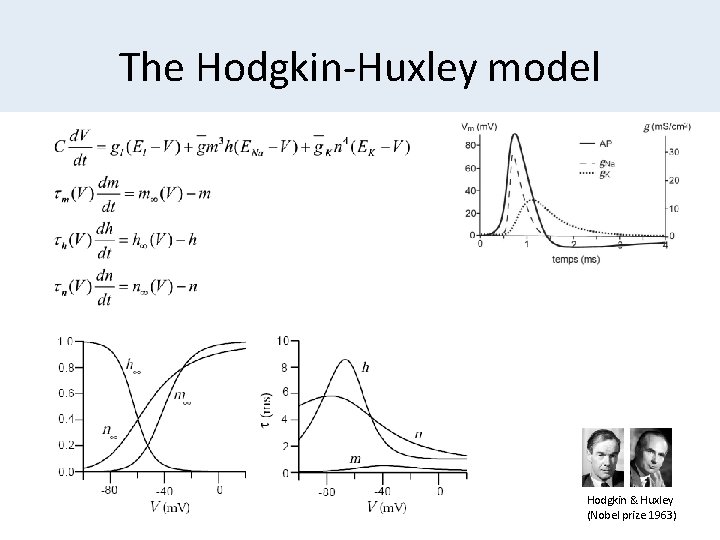
The Hodgkin-Huxley model Hodgkin & Huxley (Nobel prize 1963)

The Hodgkin-Huxley model Model of the space clamped giant squid axon Hodgkin & Huxley (Nobel prize 1963)

In what sense is it « realistic » ? several equations and variables although phenomenological! but you can make predictions about Vm, and about Na and K currents

In what sense is it « realistic » ? several equations and variables although phenomenological! you can predict voltage-clamp measurements

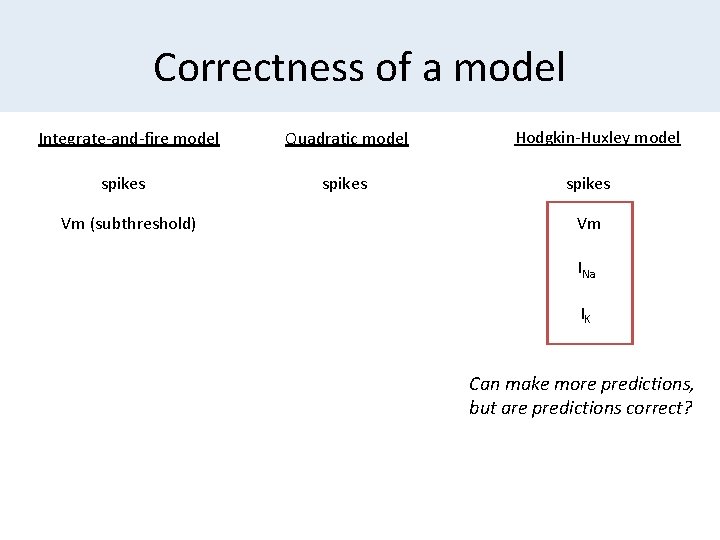
The empirical content of a model Karl Popper: “I define the empirical content of a statement p as the class of its potential falsifiers” (The logic of scientific discovery, 1935). In other words: what a model can potentially predict Integrate-and-fire model spikes Vm (subthreshold) Quadratic model spikes Hodgkin-Huxley model spikes Vm INa IK

Empirical content of neuron models empirical content multicompartmental Hodgkin-Huxley model single-compartment Hodgkin-Huxley model integrate-and-fire model exponential integrate-and-fire model quadratic integrate-and-fire model

Correctness of a model Integrate-and-fire model spikes Vm (subthreshold) Quadratic model spikes Hodgkin-Huxley model spikes Vm INa IK Can make more predictions, but are predictions correct?

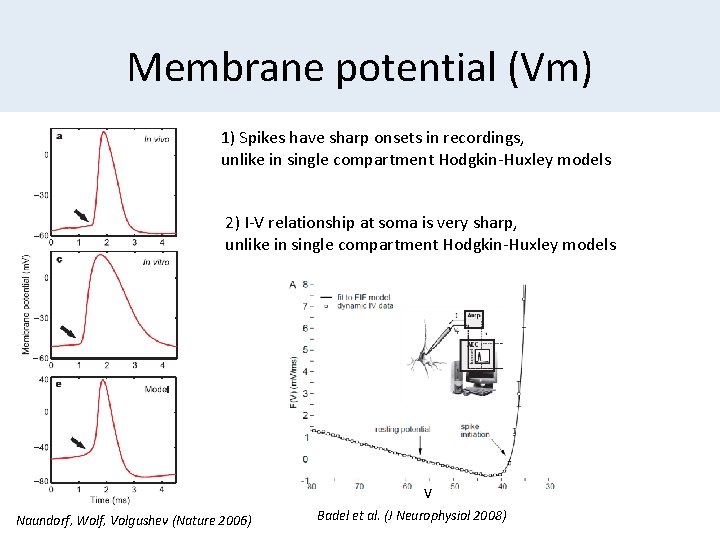
Membrane potential (Vm) 1) Spikes have sharp onsets in recordings, unlike in single compartment Hodgkin-Huxley models 2) I-V relationship at soma is very sharp, unlike in single compartment Hodgkin-Huxley models V Naundorf, Wolf, Volgushev (Nature 2006) Badel et al. (J Neurophysiol 2008)

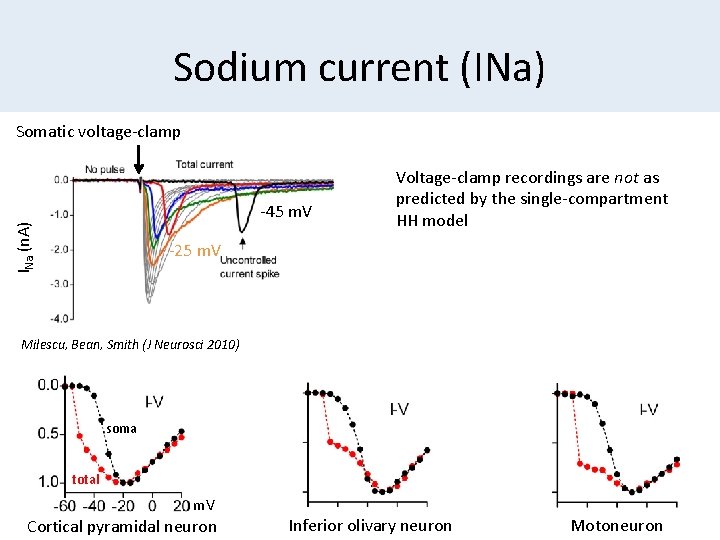
Sodium current (INa) Somatic voltage-clamp INa (n. A) -45 m. V Voltage-clamp recordings are not as predicted by the single-compartment HH model -25 m. V Milescu, Bean, Smith (J Neurosci 2010) soma total m. V Cortical pyramidal neuron Inferior olivary neuron Motoneuron

Correctness of the HH model Integrate-and-fire model spikes Vm (subthreshold) Hodgkin-Huxley model spikes Vm INa IK The additional empirical content is not correct!

Correctness of the HH model Hodgkin-Huxley model Integrate-and-fire model spikes Vm (subthreshold) Vm INa IK The additional empirical content is not correct! How about spikes?

Predicting spikes The INCF competition Gerstner & Naud (Science 2009)

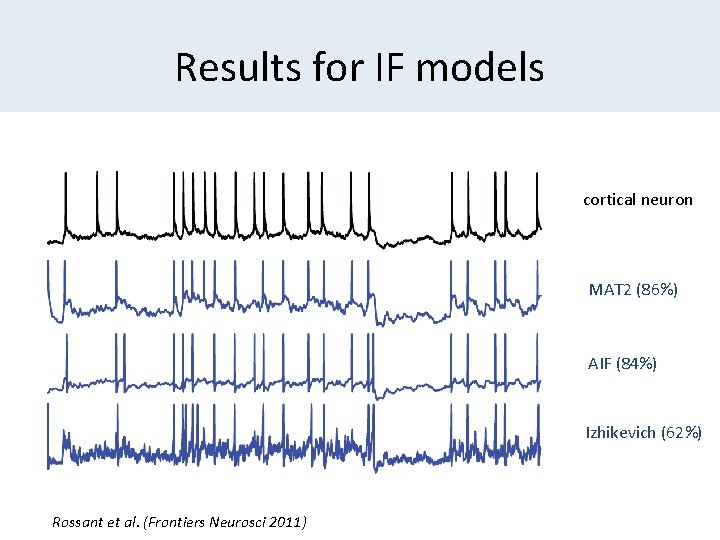
Results for IF models cortical neuron MAT 2 (86%) AIF (84%) Izhikevich (62%) Rossant et al. (Frontiers Neurosci 2011)

And the Hodgkin-Huxley model? • We did not manage to fit it • However, we did fit an approximation of it, the adaptive exponential IF model is the « slope factor » = Na activation slope ka Patch-clamp measurements: ka = 6 m. V Best prediction of spikes: = 0 m. V the best fit is an IF model! Fourcaud-Trocme et al. (J Neurosci 2003) Brette & Gerstner (J Neurophysiol 2005)

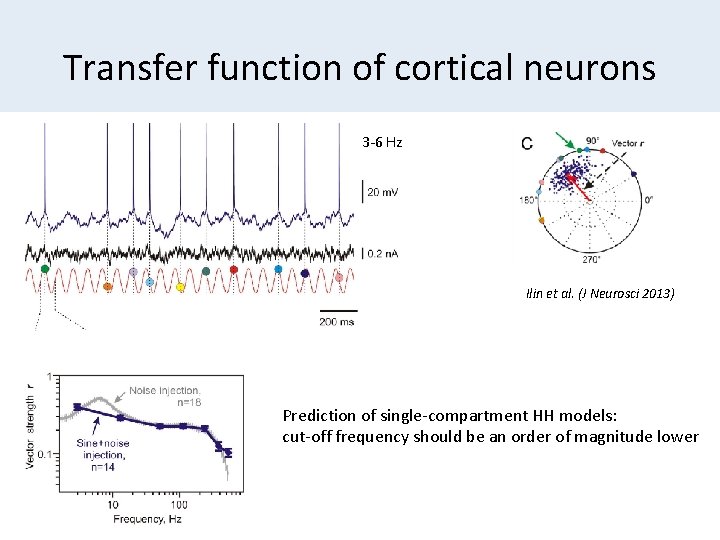
Transfer function of cortical neurons 3 -6 Hz Ilin et al. (J Neurosci 2013) Prediction of single-compartment HH models: cut-off frequency should be an order of magnitude lower

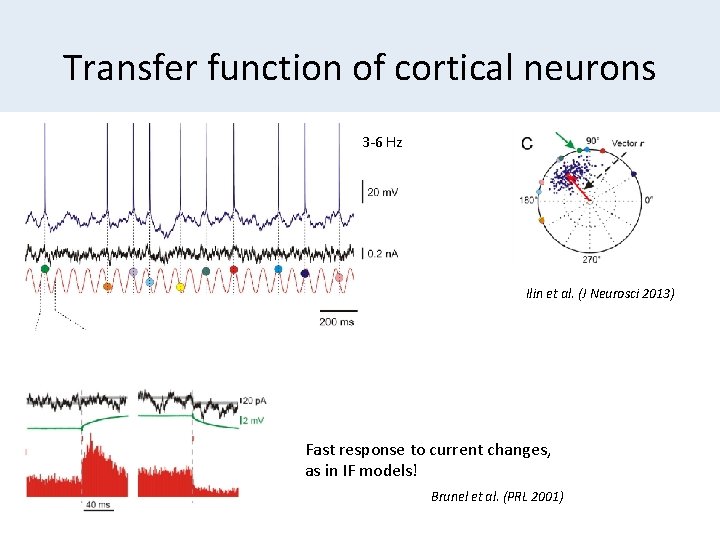
Transfer function of cortical neurons 3 -6 Hz Ilin et al. (J Neurosci 2013) Fast response to current changes, as in IF models! Brunel et al. (PRL 2001)

Correctness of the HH model Integrate-and-fire model spikes Vm (subthreshold) Hodgkin-Huxley model spikes Vm INa IK

Correctness of the HH model Integrate-and-fire model spikes Vm (subthreshold) Hodgkin-Huxley model spikes Vm INa IK Spikes are also not well predicted by the single-compartment HH model!

Correctness of neuron models correctness integrate-and-fire model exponential integrate-and-fire model single-compartment Hodgkin-Huxley model quadratic integrate-and-fire model But how is this possible ? ? ?

Spikes are initiated in the axon Stuart, Schiller, Sakmann (J Physiol 1997)

Spikes are initiated in the axon Debanne et al. (Phys Rev 2011) Stuart, Schiller, Sakmann (J Physiol 1997)

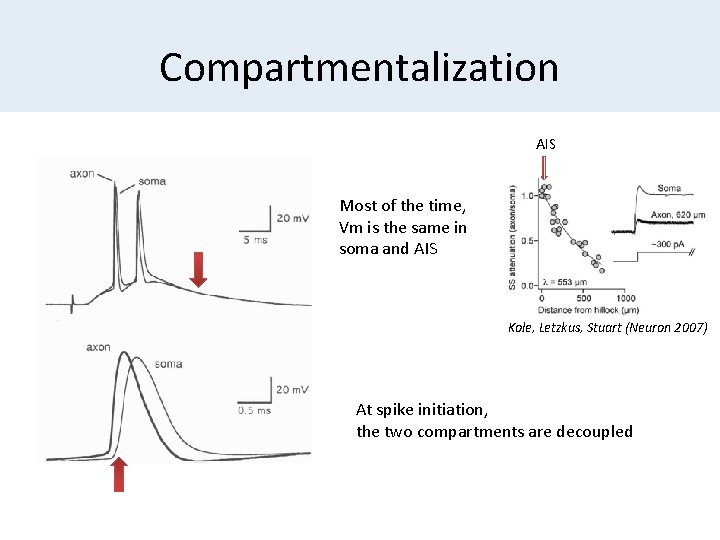
Compartmentalization AIS Most of the time, Vm is the same in soma and AIS Kole, Letzkus, Stuart (Neuron 2007) At spike initiation, the two compartments are decoupled

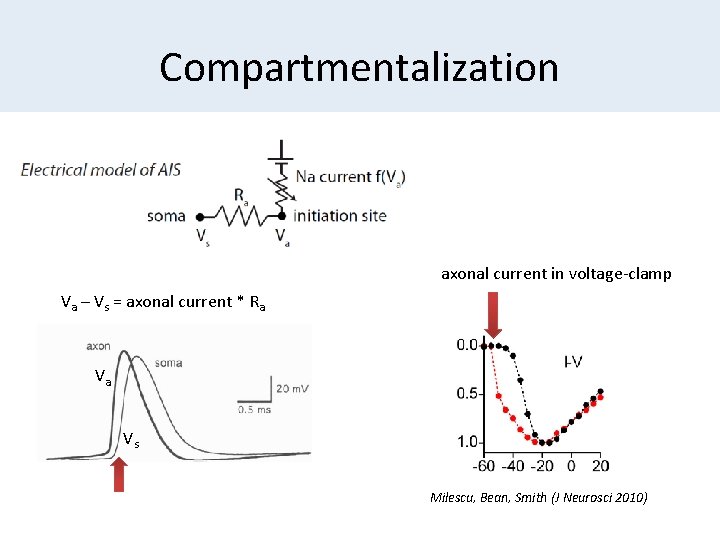
Compartmentalization axonal current in voltage-clamp Va – Vs = axonal current * Ra Va Vs Milescu, Bean, Smith (J Neurosci 2010)

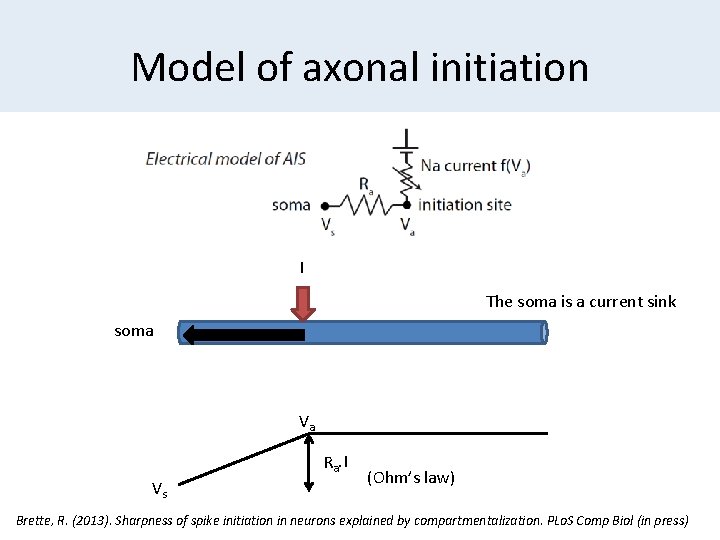
Model of axonal initiation I The soma is a current sink soma Va Ra. I Vs (Ohm’s law) Brette, R. (2013). Sharpness of spike initiation in neurons explained by compartmentalization. PLo. S Comp Biol (in press)

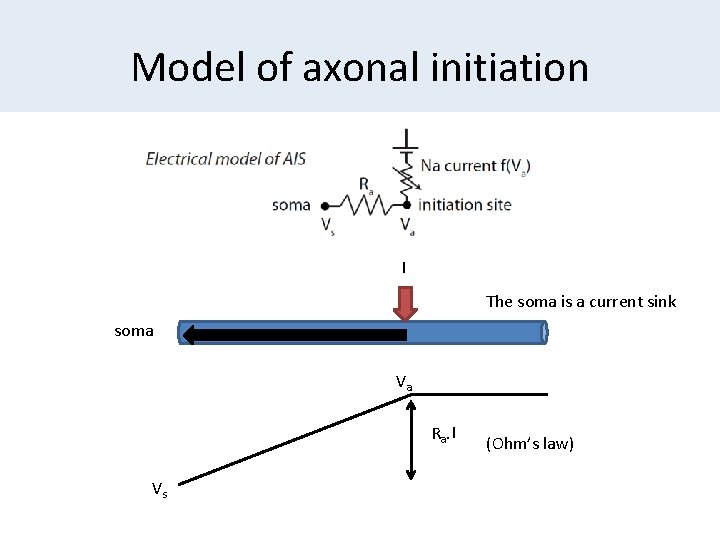
Model of axonal initiation I The soma is a current sink soma Va Ra. I Vs (Ohm’s law)

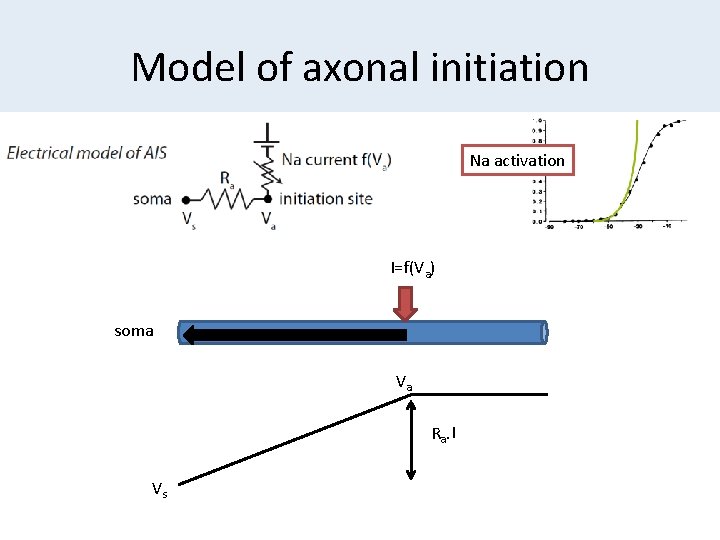
Model of axonal initiation Na activation I=f(Va) soma Va Ra. I Vs

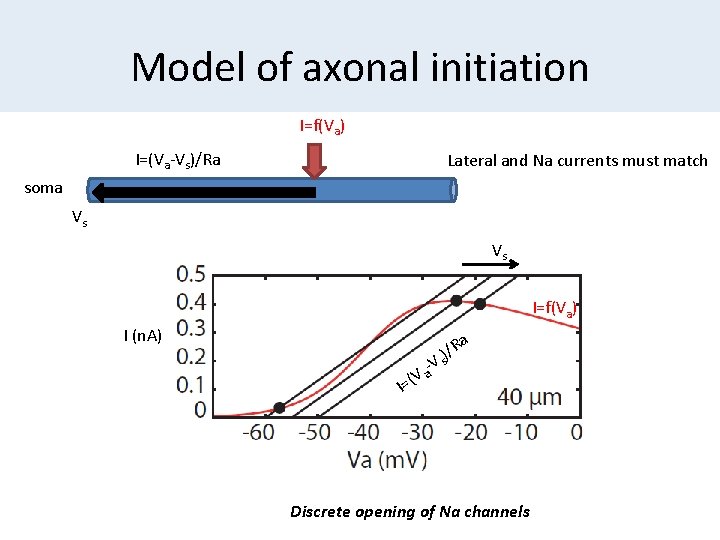
Model of axonal initiation I=f(Va) I=(Va-Vs)/Ra Lateral and Na currents must match soma Vs Vs I=f(Va) I (n. A) a a V ( I= /R ) s V Discrete opening of Na channels

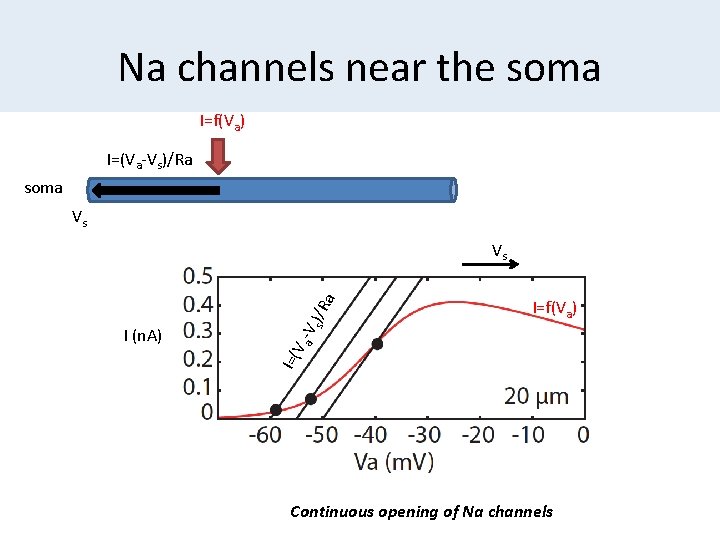
Na channels near the soma I=f(Va) I=(Va-Vs)/Ra soma Vs I=f(Va) I=( V I (n. A) a -V s )/R a Vs Continuous opening of Na channels

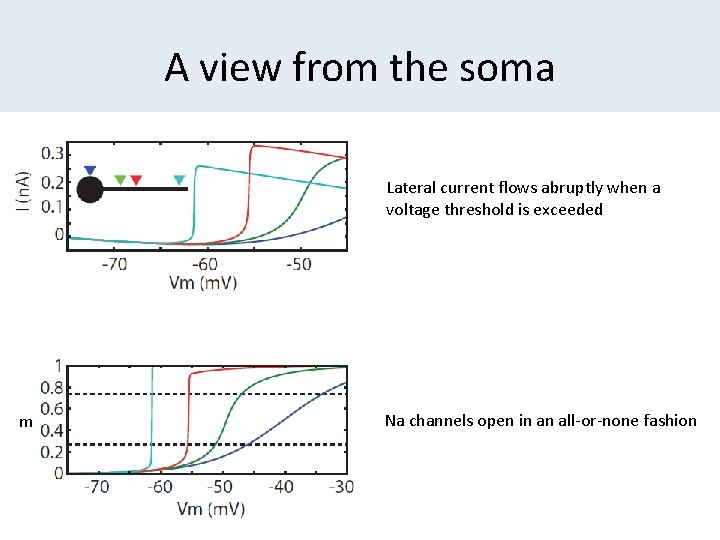
A view from the soma Lateral current flows abruptly when a voltage threshold is exceeded m Na channels open in an all-or-none fashion

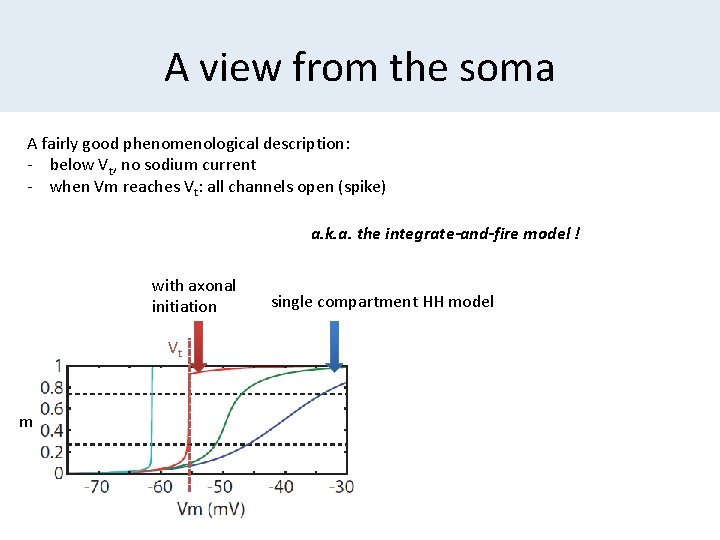
A view from the soma A fairly good phenomenological description: - below Vt, no sodium current - when Vm reaches Vt: all channels open (spike) a. k. a. the integrate-and-fire model ! with axonal initiation Vt m single compartment HH model

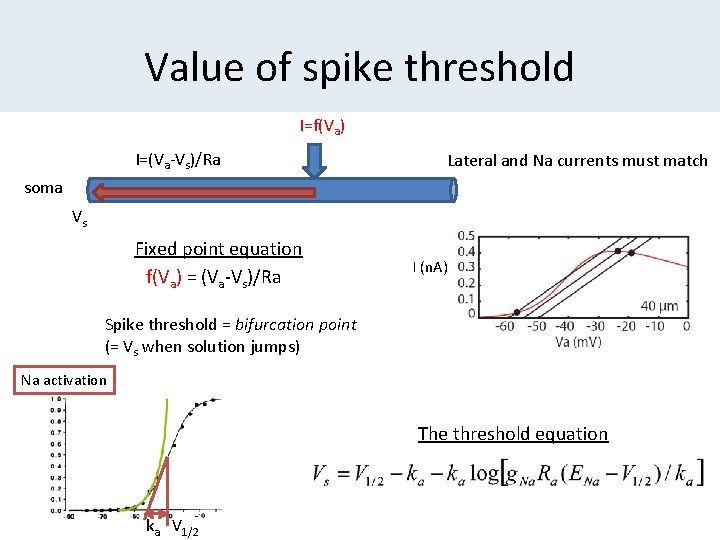
Value of spike threshold I=f(Va) I=(Va-Vs)/Ra Lateral and Na currents must match soma Vs Fixed point equation f(Va) = (Va-Vs)/Ra I (n. A) Spike threshold = bifurcation point (= Vs when solution jumps) Na activation The threshold equation ka V 1/2

Conclusion Single-compartment Hodgkin-Huxley model looks good but doesn’t fly! Integrate-and-fire model it flies! Brette R (2015). What Is the Most Realistic Single-Compartment Model of Spike Initiation? PLo. S Comput Biol. 2015 Apr 9; 11(4): e 1004114. Brette, R. (2013). Sharpness of spike initiation in neurons explained by compartmentalization. PLo. S Comp Biol, doi: 10. 1371/journal. pcbi. 1003338.