What is the language of single cells What

What is the language of single cells? What are the elementary symbols of the code? Most typically, we think about the response as a firing rate, r(t), or a modulated spiking probability, P(r = spike|s(t)). Two extremes of description: A Poisson model, where spikes are generated randomly with rate r(t). However, most spike trains are not Poisson (refractoriness, internal dynamics). Fine temporal structure might be meaningful. àConsider spike patterns or “words”, e. g. • symbols including multiple spikes and the interval between • retinal ganglion cells: “when” and “how much”

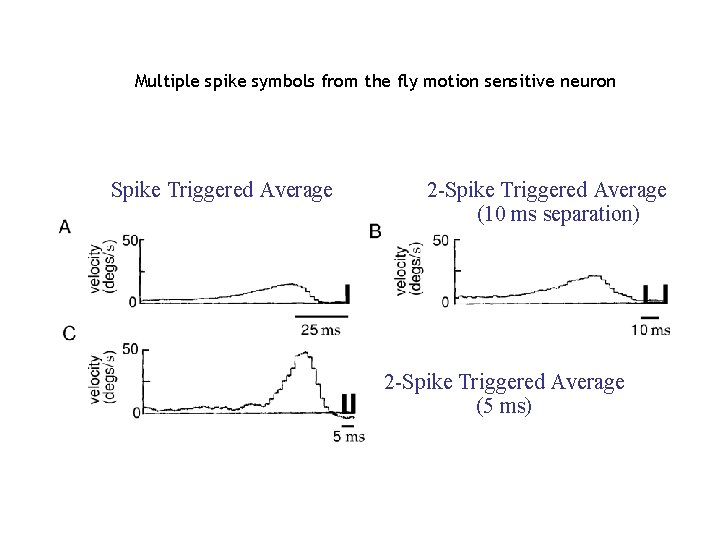
Multiple spike symbols from the fly motion sensitive neuron Spike Triggered Average 2 -Spike Triggered Average (10 ms separation) 2 -Spike Triggered Average (5 ms)

Spike statistics Stochastic process that generates a sequence of events: point process Probability of an event at time t depends only on preceding event: renewal process All events are statistically independent: Poisson process Poisson: r(t) = r independent of time, probability to see a spike only depends on the time you watch. PT[n] = (r. T)n exp(-r. T)/n! Exercise: the mean of this distribution is r. T the variance of this distribution is also r. T. The Fano factor = variance/mean = 1 for Poisson processes. The Cv = coefficient of variation = STD/mean = 1 for Poisson Interspike interval distribution P(T) = r exp(-r. T)

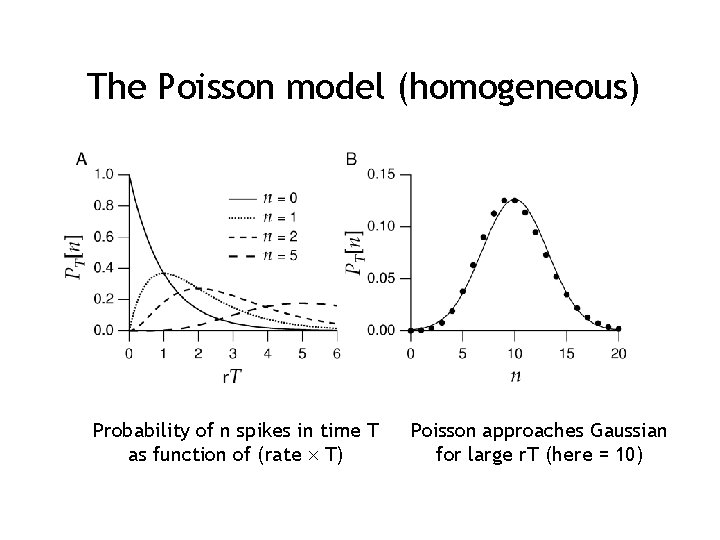
The Poisson model (homogeneous) Probability of n spikes in time T as function of (rate T) Poisson approaches Gaussian for large r. T (here = 10)

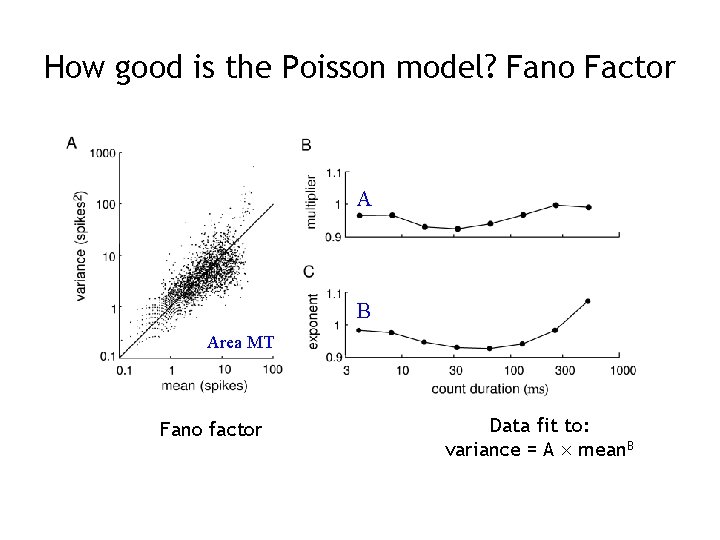
How good is the Poisson model? Fano Factor A B Area MT Fano factor Data fit to: variance = A mean. B

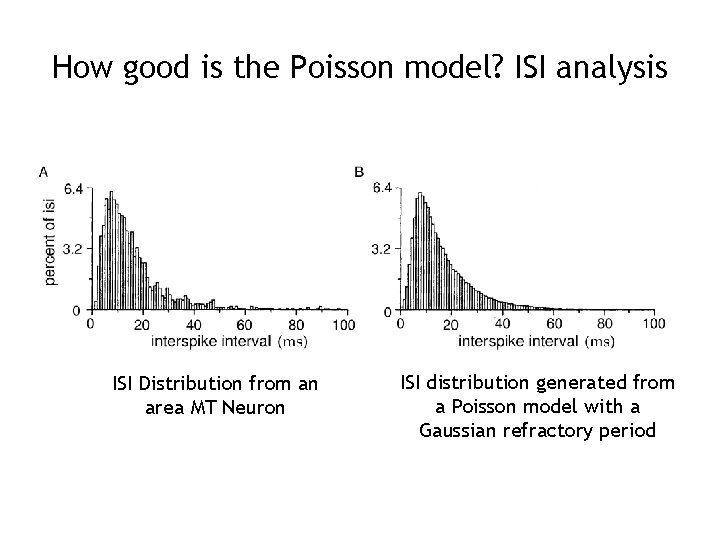
How good is the Poisson model? ISI analysis ISI Distribution from an area MT Neuron ISI distribution generated from a Poisson model with a Gaussian refractory period

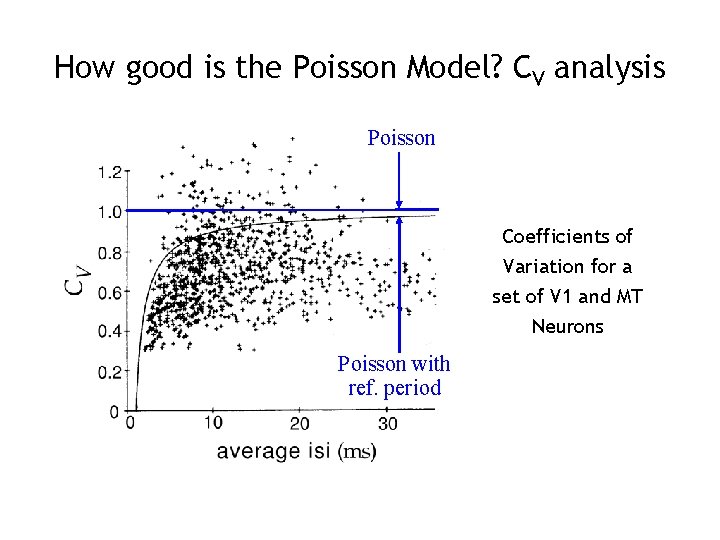
How good is the Poisson Model? CV analysis Poisson Coefficients of Variation for a set of V 1 and MT Neurons Poisson with ref. period

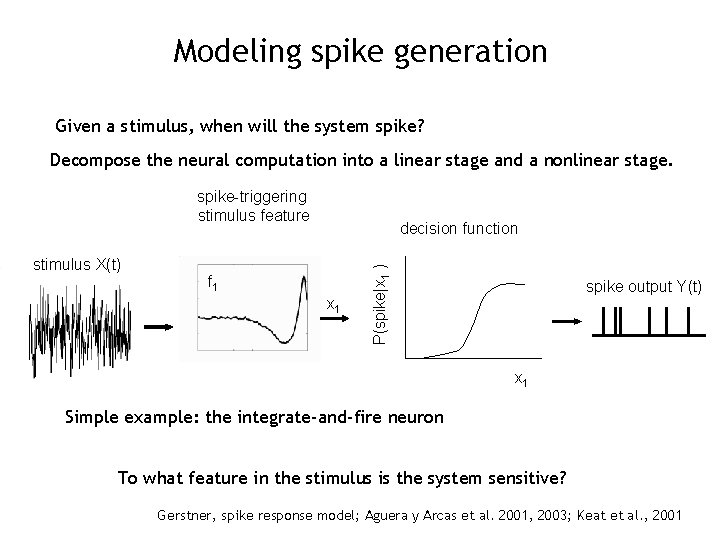
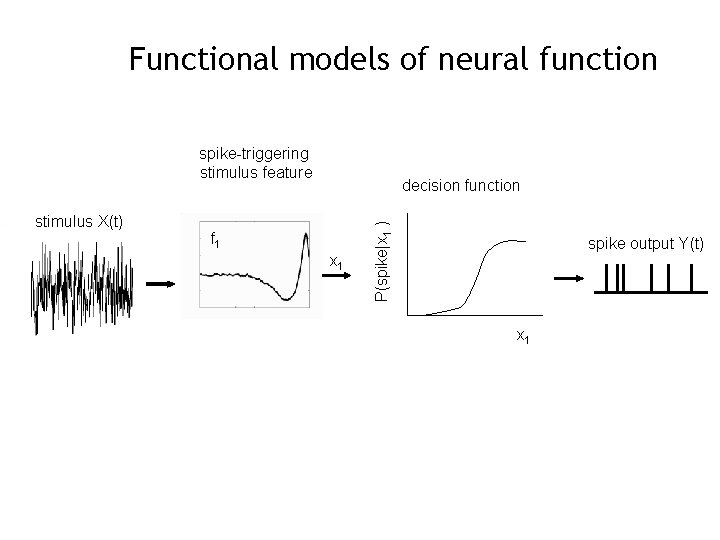
Modeling spike generation Given a stimulus, when will the system spike? Decompose the neural computation into a linear stage and a nonlinear stage. spike-triggering stimulus feature f 1 x 1 P(spike|x 1 ) stimulus X(t) decision function spike output Y(t) x 1 Simple example: the integrate-and-fire neuron To what feature in the stimulus is the system sensitive? Gerstner, spike response model; Aguera y Arcas et al. 2001, 2003; Keat et al. , 2001

Predicting the firing rate Let’s start with a rate response, r(t) and a stimulus, s(t). The optimal linear estimator is closest to satisfying Want to solve for K. Multiply by s(t-t’) and integrate over t: Note that we have produced terms which are simply correlation functions: Given a convolution, Fourier transform: Now we have a straightforward algebraic equation for K(w): Solving for K(t),

Predicting the firing rate Going back to: For white noise, the correlation function Css(t) = s 2 d(t), So K(t) is simply Crs(t).

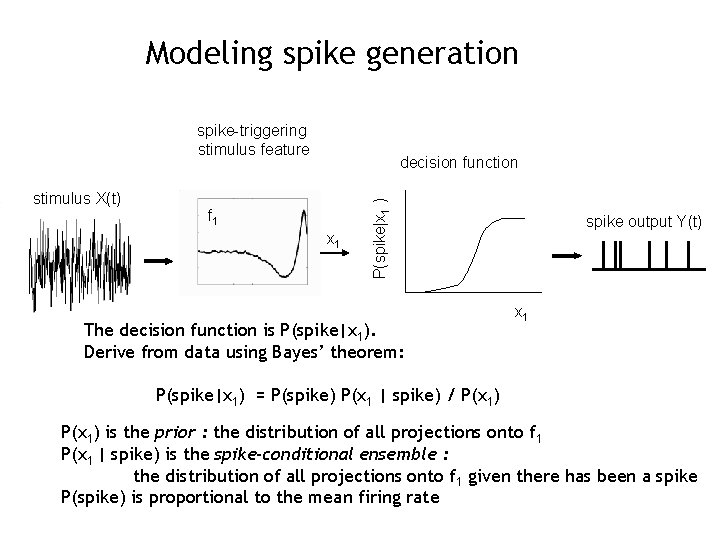
Modeling spike generation spike-triggering stimulus feature f 1 x 1 P(spike|x 1 ) stimulus X(t) decision function The decision function is P(spike|x 1). Derive from data using Bayes’ theorem: spike output Y(t) x 1 P(spike|x 1) = P(spike) P(x 1 | spike) / P(x 1) is the prior : the distribution of all projections onto f 1 P(x 1 | spike) is the spike-conditional ensemble : the distribution of all projections onto f 1 given there has been a spike P(spike) is proportional to the mean firing rate

Models of neural function spike-triggering stimulus feature f 1 x 1 P(spike|x 1 ) stimulus X(t) decision function spike output Y(t) x 1 Weaknesses

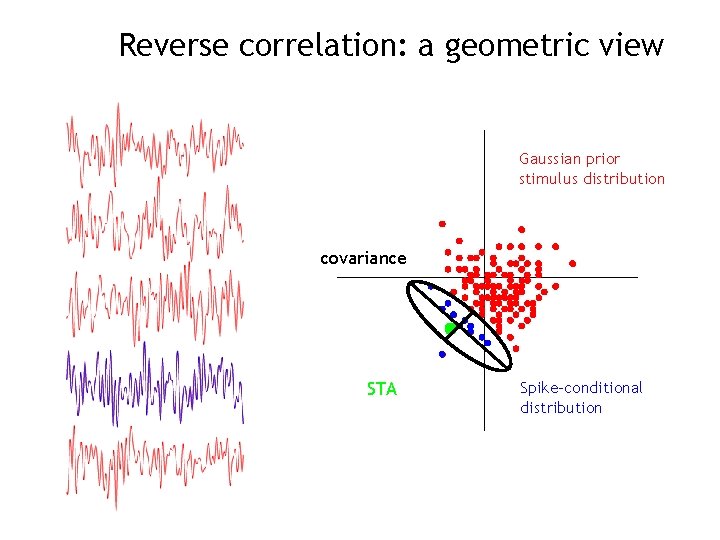
Reverse correlation: a geometric view Gaussian prior stimulus distribution covariance STA Spike-conditional distribution

Dimensionality reduction The covariance matrix is simply Cij = < S(t – ti) S(t - tj)> - < STA(t - ti) STA (t - tj)> - < I(t - ti) I(t - tj)> Stimulus prior Properties: • If the computation is low-dimensional, there will be a few eigenvalues significantly different from zero • The number of eigenvalues is the relevant dimensionality • The corresponding eigenvectors span the subspace of the relevant features Bialek et al. , 1997

Functional models of neural function spike-triggering stimulus feature f 1 x 1 P(spike|x 1 ) stimulus X(t) decision function spike output Y(t) x 1

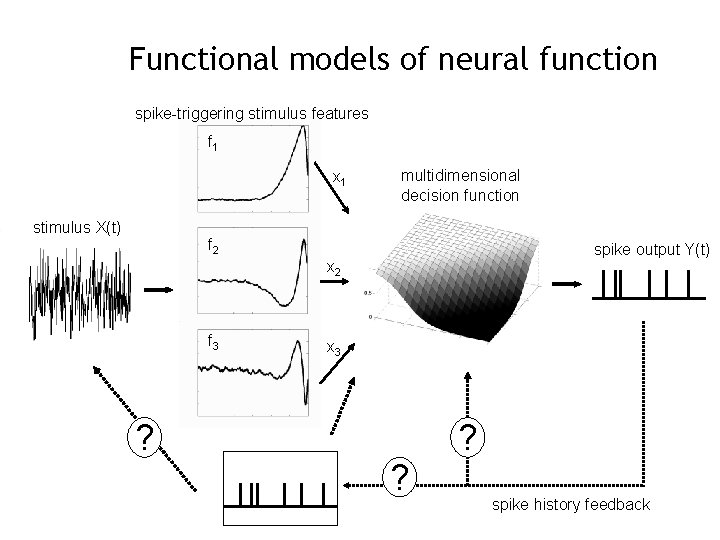
Functional models of neural function spike-triggering stimulus features f 1 x 1 stimulus X(t) f 2 x 2 f 3 x 3 multidimensional decision function spike output Y(t)

Functional models of neural function spike-triggering stimulus features f 1 x 1 stimulus X(t) multidimensional decision function f 2 spike output Y(t) x 2 f 3 ? x 3 ? ? spike history feedback

Covariance analysis Let’s develop some intuition for how this works: the Keat model Keat, Reinagel, Reid and Meister, Predicting every spike. Neuron (2001) • Spiking is controlled by a single filter • Spikes happen generally on an upward threshold crossing of the filtered stimulus expect 2 modes, the filter F(t) and its time derivative F’(t)

Covariance analysis

Covariance analysis Let’s try some real neurons: rat somatosensory cortex (Ras Petersen, Mathew Diamond, SISSA: Sf. N 2003). Record from single units in barrel cortex

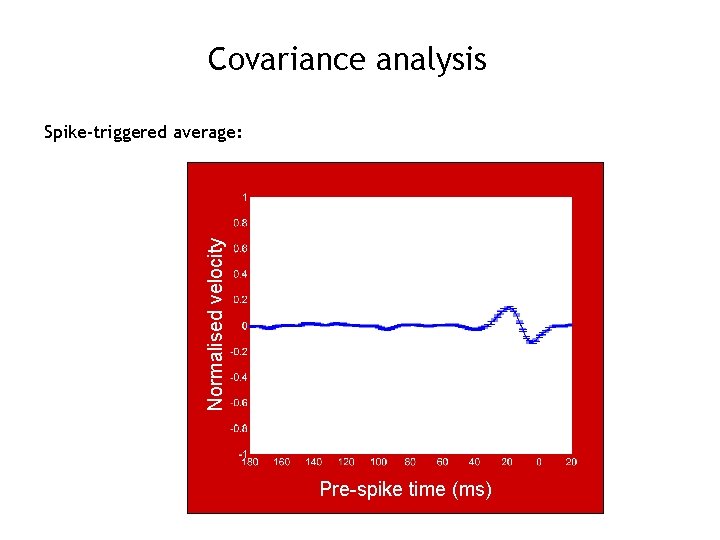
Covariance analysis Normalised velocity Spike-triggered average: Pre-spike time (ms)

Covariance analysis Is the neuron simply not very responsive to a white noise stimulus?

Covariance analysis Prior Spiketriggered Difference

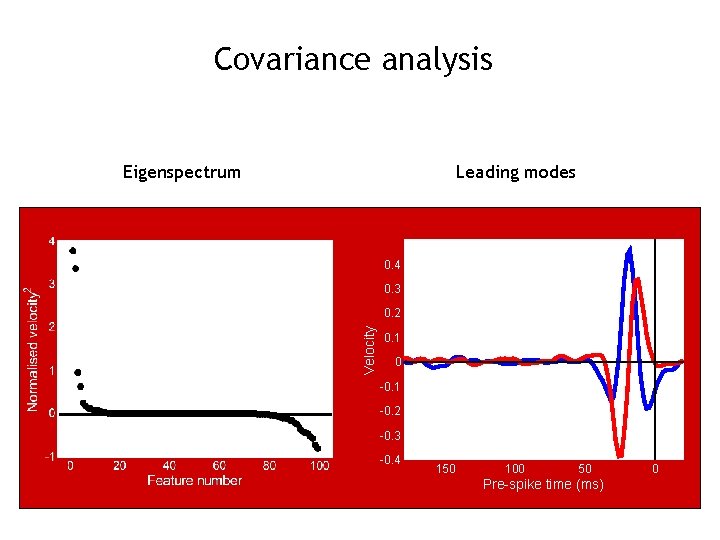
Covariance analysis Eigenspectrum Leading modes 0. 4 0. 3 Velocity 0. 2 0. 1 0 -0. 1 -0. 2 -0. 3 -0. 4 150 100 50 Pre-spike time (ms) 0

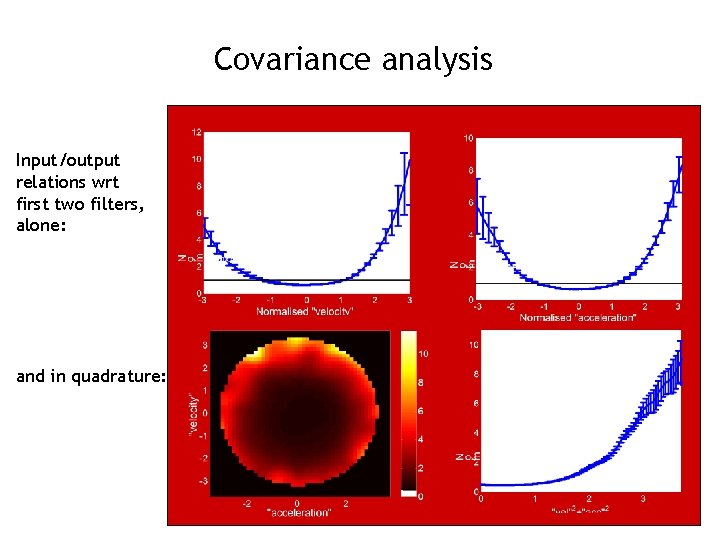
Covariance analysis Input/output relations wrt first two filters, alone: and in quadrature:

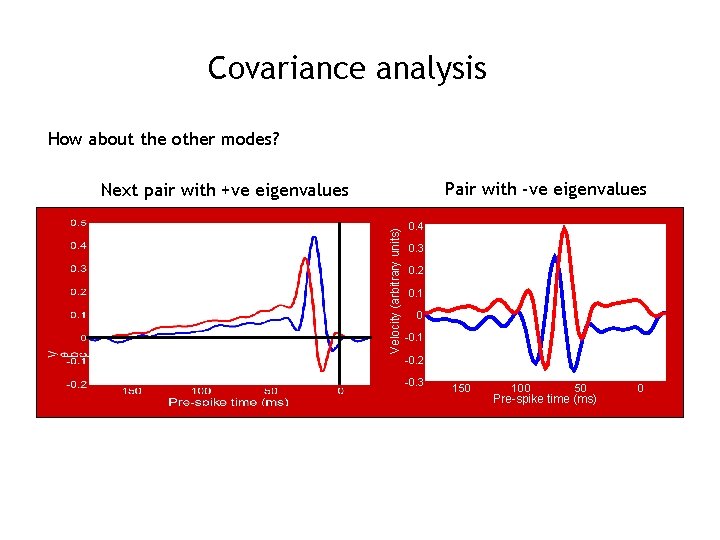
Covariance analysis How about the other modes? Pair with -ve eigenvalues Velocity (arbitrary units) Next pair with +ve eigenvalues 0. 4 0. 3 0. 2 0. 1 0 -0. 1 -0. 2 -0. 3 150 100 50 Pre-spike time (ms) 0

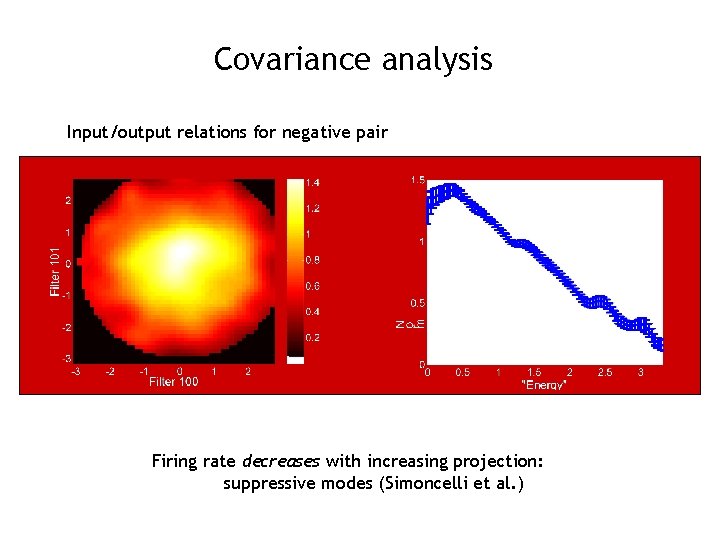
Covariance analysis Input/output relations for negative pair Firing rate decreases with increasing projection: suppressive modes (Simoncelli et al. )