What is the Fastest Sorting Algorithm A Computer

What is the Fastest Sorting Algorithm? A Computer Science Project by Timothy Hewitt

About Me I am a 9 th grade, self-professed, computer geek. I enjoy physics, chemistry, as well as all types of math. A few of the FLVS courses I've completed include Algebra II, Computer Programming 1, and M/J Comprehensive Science 3. I'm currently taking Physical Science and AP Computer Science A.

Project Introduction This project attempts to tackle, in a real-life scenario, which of the common sorting algorithms is the fastest. I was inspired to do this particular question because I was just finishing up the section on sorting in AP Computer Science when I decided to participate in the science fair. My theory is that the merge sort will be faster overall even though other methods will be faster on certain arrangements of data.

Definitions n – the number of items in a list Iteration – one execution of the code inside a loop k – number of iterations of a loop that have been executed log – short for logarithm, mathematical inverse of exponents Python – the programming language I used to do this project

Hypothesis My hypothesis is that the merge sort will be the fastest overall because of it's low and constant theoretical runtime of n log n, while other methods may be faster on specific orderings of input data.

Initial Research Selection Sort The selection sort finds the smallest remaining item and then swaps it with the next location to be filled. Since it uses two nested loops, it runs in quadratic time (for a list of length n, it takes n 2 iterations to complete). After k iterations of the main loop, the first k elements are in their final sorted position.

Initial Research Insertion Sort The insertion sort takes each item in the list and inserts the item where it's sorted when compared to the previous elements. This algorithm also runs in quadratic time since it too uses two nested loops. After k iterations of the outer loop, the first k elements will be sorted, but not in their final locations.

Initial Research Merge Sort The merge sort is a recursive algorithm, it uses itself in it's definition. The algorithm takes a list and splits it, then merge sorts both halves. When done, it merges the two lists back together so that the items are in the right order. This algorithm runs in n log n time because of it's recursive nature. This algorithm's theoretical runtime does not differ based on the order of the data.

Initial Research Quicksort The quicksort is also recursive, but it instead selects one element, then puts all of the elements less than that element on one side, and all the ones greater than it on the other, it then quicksorts both of the sides. This algorithm does the best on an evenly mixed list, running in n log n time theoreticaly. The worst case is an ordered list, where it goes to quadratic time, no matter which direction the data is arranged.

Initial Research Real-life Application Sorting methods are used everywhere Web Searches Playlist Ordering Employee Searches Database Queries and each situation may need a different style of algorithm. Based on this research, my hypothesis that the merge sort will be the fastest overall even if other

Materials & Procedure Materials Procedure Computer with python 2. 7 installed – Download here 1. Exit all running programs, status updaters and background applications Experiment Program – Download here 2. Run test program 3. Crunch the numbers!

What does the program do? Each algorithm is used on three sets of data, ascending, mixed, and descending. In order to have a useful time, a copy of the data is sorted 1000 times per trial, as a single sort would be too fast to measure. The program does five trials per data set, for each sorting method, resulting in 60 data points.

Data Ascending When the data was in ascending order, the insertion sort was almost instantaneous, at 130. 9 milliseconds Take a look at how close the quicksort and selection sort are, demonstrating how a quicksort increases to quadratic time.

Data Mixed Now, for the mixed data, the quicksort had this in the bag, at 450. 3 milliseconds. Check out how much slower the inserion sort is, as well as how little the merge sort changed, only a tenth of a second or so.

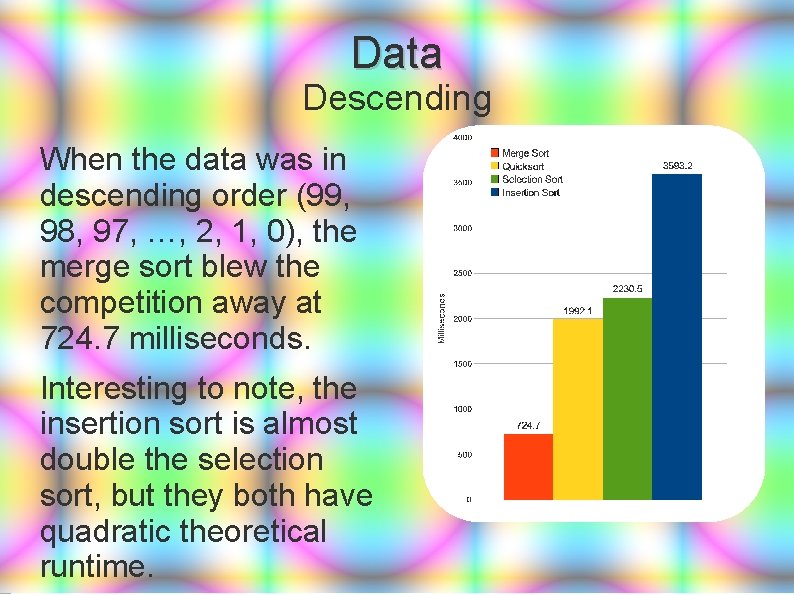
Data Descending When the data was in descending order (99, 98, 97, …, 2, 1, 0), the merge sort blew the competition away at 724. 7 milliseconds. Interesting to note, the insertion sort is almost double the selection sort, but they both have quadratic theoretical runtime.

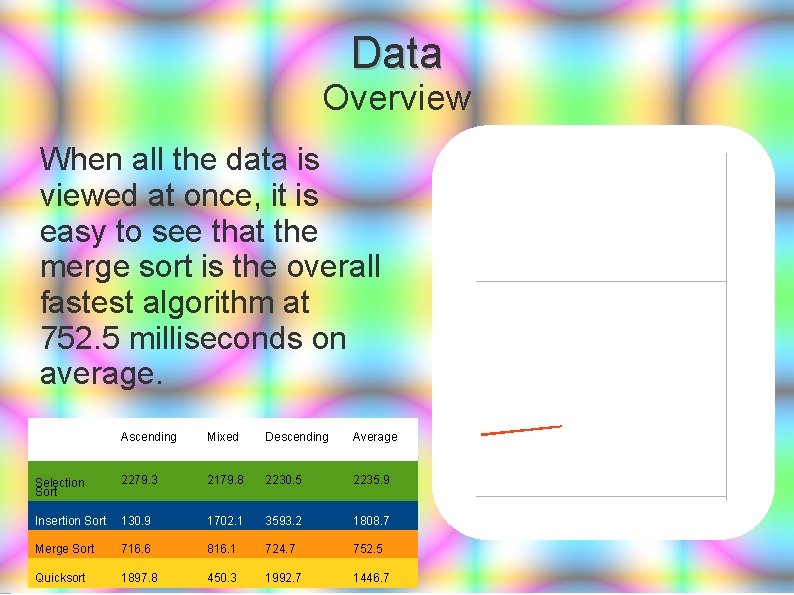
Data Overview When all the data is viewed at once, it is easy to see that the merge sort is the overall fastest algorithm at 752. 5 milliseconds on average. Ascending Mixed Descending Average Selection Sort 2279. 3 2179. 8 2230. 5 2235. 9 Insertion Sort 130. 9 1702. 1 3593. 2 1808. 7 Merge Sort 716. 6 816. 1 724. 7 752. 5 Quicksort 1897. 8 450. 3 1992. 7 1446. 7

Discussion The runtime for an insertion sort shoots up once a single element is out of a place, as it now has to do many more comparisons and moves. Much time can be shaved off of a quicksort algorithm by adding in another method to find a suitable midpoint, but I elected to use the basic implementation. While the exact times may differ on another computer, the end result of this experiment should be the same because the same algorithms are being tested.

Conclusion Through this experiment, I found that while the inserton sort (avg. 1808. 7 millis. ) and quicksort (avg. 1446. 7 millis. ) both had very fast times in some places, they were much slower on other arrangements. This leaves the selection sort and the merge sort, both very stable, but the merge sort was much faster, 752. 5 milliseconds versus 2235. 9 milliseconds, making it the fastest of the algorithms that I tested. This result supports the hypothesis that I posed earlier.

Acknowledgements • Both my parents, for giving advice on the presentation itself. • Mr. Jordan, my Computer Programming 1 and AP Computer Science teacher, for improving my coding abilities. • Guido van Rossum, creator of Python, for making such a powerful, simple, and easy to use programming language.

Bibliography Conrado Martinez, "quicksort", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed. , U. S. National Institute of Standards and Technology. 24 August 2009. (accessed 3/21/2011) Available from: http: //www. nist. gov/dads/HTML/quicksort. html Paul E. Black, "insertion sort", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed. , U. S. National Institute of Standards and Technology. 24 January 2011. (accessed 3/21/2011) Available from: http: //www. nist. gov/dads/HTML/insertion. Sort. html Paul E. Black, "selection sort", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed. , U. S. National Institute of Standards and Technology. 24 August 2009. (accessed 3/21/2011) Available from: http: //www. nist. gov/dads/HTML/selection. Sort. html Paul E. Black, "merge sort", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed. , U. S. National Institute of Standards and Technology. 24 August 2009. (accessed 3/21/2011) Available from: http: //www. nist. gov/dads/HTML/mergesort. html Self-experience with algorithms from AP Computer Science A, started November 2010, finishing April 2011.