What is the Best MultiStage Architecture for Object

What is the Best Multi-Stage Architecture for Object Recognition Kevin Jarrett, Koray Kavukcuoglu, Marc’ Aurelio Ranzato and Yann Le. Cun Presented by Lingbo Li ECE, Duke University Dec. 13 rd, 2010

Outline • • Introduction Model Architecture Training Protocol Experiments Ø Caltech 101 Dataset Ø NORB Dataset Ø MNIST Dataset • Conclusions

Introduction (I) Feature extraction stages: Ø A filter bank Ø A non-linear operation Ø A pooling operation Recognition architectures: • Single stage of features + supervised classifier: SIFT, Ho. G, etc. • Two or more successive stages of feature extractors + supervised classifier: convolutional networks

Introduction (II) • Q 1: How do the non-linearities that follow the filter banks influence the recognition accuracy? • Q 2: Is there any advantage to using an architecture with two successive stages of features extraction, rather than with a single stage? • Q 3: Does learning the filter banks in an unsupervised or supervised manner improve the performance over hardwired filters or even random filters?

Model Architecture (I) • Input: Output: is the j-th feature map Filter : A filter bank layer with 64 filters of size 9 x 9 :

Model Architecture (II) • • Ø Subtractive normalization operation Ø Divisive normalization operation

Model Architecture (III) • An average pooling layer with 4 x 4 down-sampling: • A max-pooling layer with 4 x 4 down-sampling:

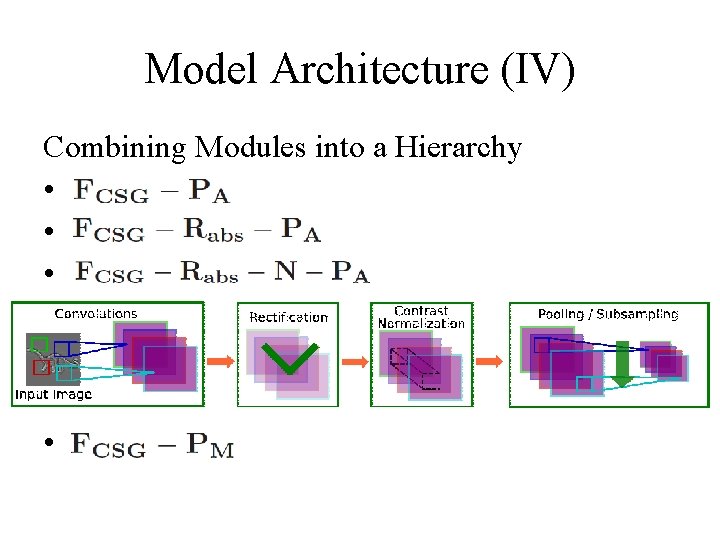
Model Architecture (IV) Combining Modules into a Hierarchy • •

Training Protocol (I) Optimal sparse coding: Under sparse condition, this problem can be written as an optimization problem: Given training samples 1) Minimize the loss function , learning proceeds: 2) Find by running a rather expensive optimization algorithm.

Training Protocol (II) Predictive Sparse Decomposition (PSD) PSD trains a regressor to approximate the sparse solution for all training samples, where Learning proceeds by minimizing the loss function where Thus, (dictionary) and optimized. (filters) are simultaneously

Training Protocol (III) A single letter: an architecture with a single stage of feature extraction followed by a classifier; A double letter: an architecture with two stages if feature extraction followed by a classifier. q Filters are set to random values and kept fixed. Classifiers are trained in supervised mode. q Filters are trained using unsupervised PSD algorithm, and kept fixed. Classifiers are trained in supervised model. q Filters are initialized with random values. The entire system (Feature stages + classifiers) is trained in supervised mode with gradient descent. q Filters are initialized with the PSD unsupervised learning algorithm. The entire system (feature stages + classifiers) is trained in supervised mode by gradient descent.

Experiments (I) – Caltech 101 • Data pre-processing: 1) 2) 3) 4) Convert to gray-scale and resize to 151 x 151 pixels; Subtract the image mean and divide by the image standard deviation; Apply subtractive/divisive normalization (N layer with c=1); Zero-padding the shorter side to 143 pixels. • Recognition rates are averaged over 5 drawings of the training set (30 images per class). • Hyper-parameters are selected to maximize the performance on the validation set of 5 samples per class taken out of the training sets.

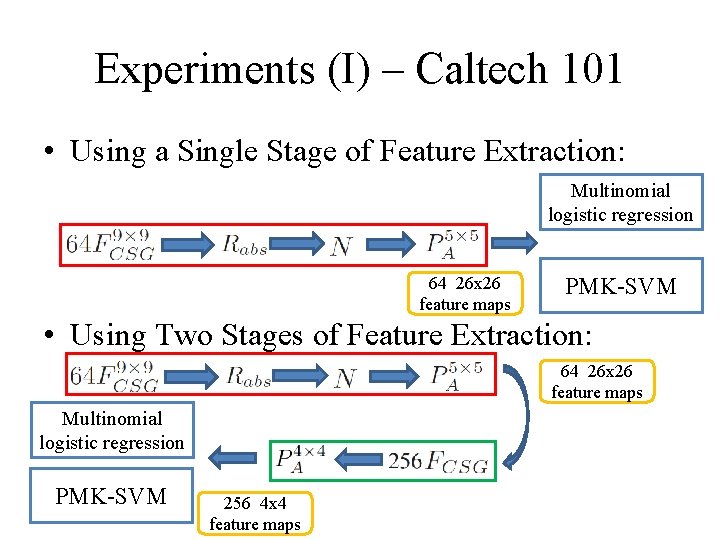
Experiments (I) – Caltech 101 • Using a Single Stage of Feature Extraction: Multinomial logistic regression 64 26 x 26 feature maps PMK-SVM • Using Two Stages of Feature Extraction: 64 26 x 26 feature maps Multinomial logistic regression PMK-SVM 256 4 x 4 feature maps

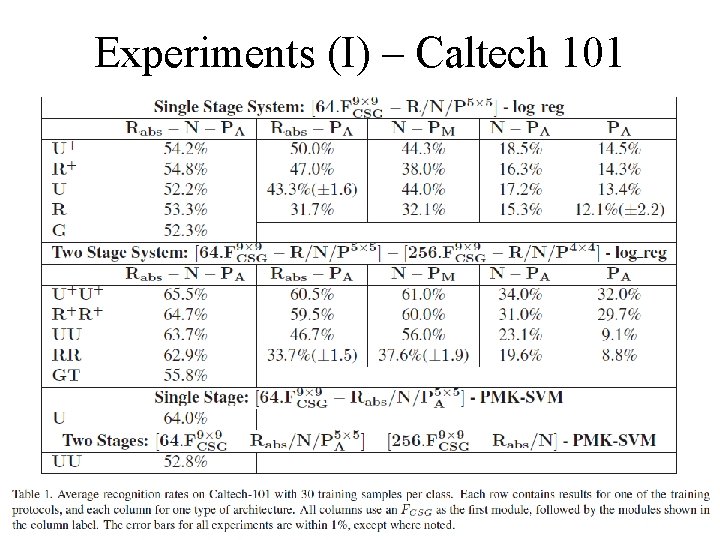
Experiments (I) – Caltech 101

Experiments (I) – Caltech 101 • Random filters and no filter learning whatsoever with can achieve decent performance; • Supervised fine tuning improves the performance; • Two-stage systems are better than their single-stage counterparts; • With rectification and normalization , unsupervised training does not improve the performance; • abs rectification is a crucial component for good performance; • Single-stage system with PMK-SVM reaches the same performance with a two-stage with logistic regression;

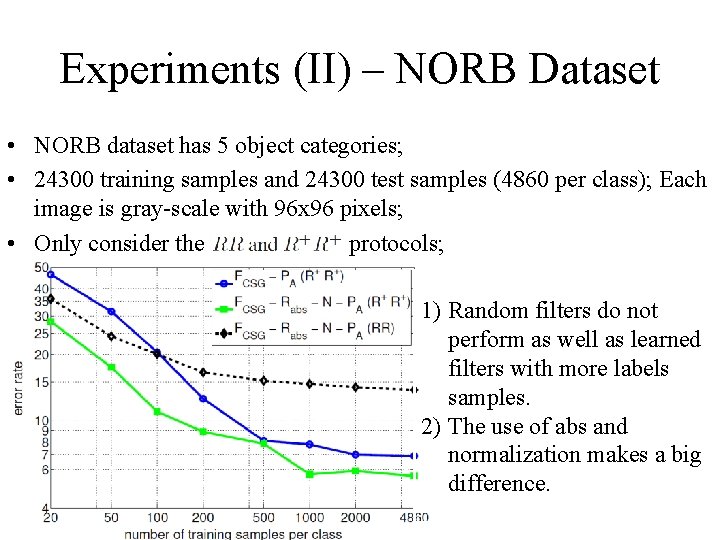
Experiments (II) – NORB Dataset • NORB dataset has 5 object categories; • 24300 training samples and 24300 test samples (4860 per class); Each image is gray-scale with 96 x 96 pixels; • Only consider the protocols; 1) Random filters do not perform as well as learned filters with more labels samples. 2) The use of abs and normalization makes a big difference.

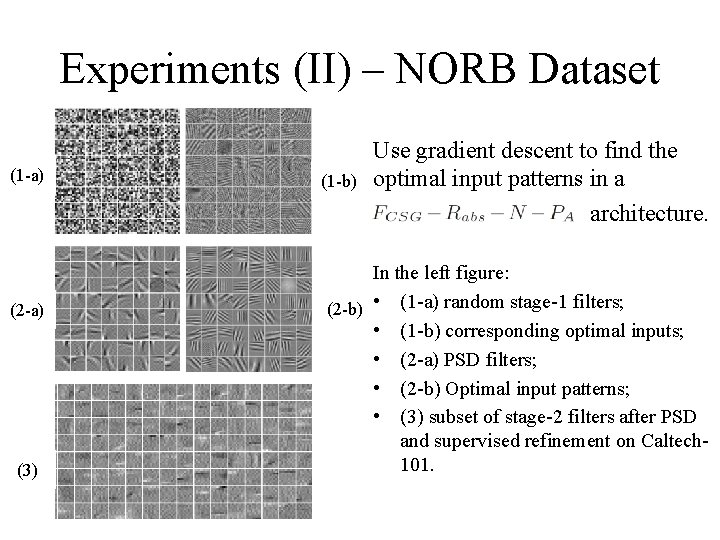
Experiments (II) – NORB Dataset (1 -a) (2 -a) (3) (1 -b) Use gradient descent to find the optimal input patterns in a architecture. In the left figure: (2 -b) • (1 -a) random stage-1 filters; • (1 -b) corresponding optimal inputs; • (2 -a) PSD filters; • (2 -b) Optimal input patterns; • (3) subset of stage-2 filters after PSD and supervised refinement on Caltech 101.

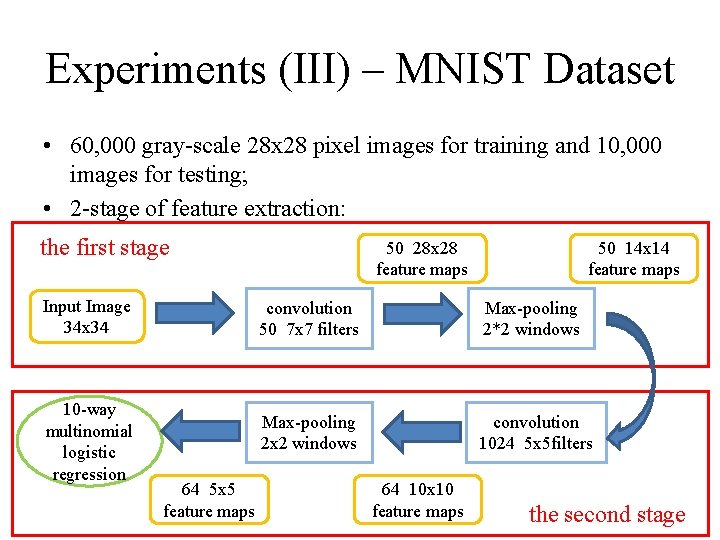
Experiments (III) – MNIST Dataset • 60, 000 gray-scale 28 x 28 pixel images for training and 10, 000 images for testing; • 2 -stage of feature extraction: the first stage Input Image 34 x 34 10 -way multinomial logistic regression 64 5 x 5 feature maps 50 28 x 28 feature maps 50 14 x 14 feature maps convolution 50 7 x 7 filters Max-pooling 2*2 windows Max-pooling 2 x 2 windows convolution 1024 5 x 5 filters 64 10 x 10 feature maps the second stage

Experiments (III) – MNIST Dataset • Parameters are trained with PSD: the only hyperparameter is tuned with a validation set of 10, 000 training samples. • The classifier is randomly initialized; • The whole system is tuned in supervised mode. • A test error rate of 0. 53% was obtained.

Conclusions (I) • Q 1: How do the non-linearities that follow the filter banks influence the recognition accuracy? 1) A rectifying non-linearity is the single most important factor. 2) A local normalization layer can also improve the performance. • Q 2: Is there any advantage to using an architecture with two successive stages of feature extraction, rather than with a single stage? 1) Two stages are better than one. 2) The performance of two-stage system is similar to that of the best single-stage systems based on SIFT and PMK-SVM.

Conclusions (II) • Q 3: Does learning the filter banks in an unsupervised or supervised manner improve the performance over hard-wired filters or even random filters? 1) Random filters yield good performance only in the case of small training set. 2) The optimal input patterns for a randomly initialized stage are similar to the optimal inputs for a stage that use learned filters. 3) The global supervised learning of filters yields good recognition rate if with the proper non-linearites. 4) Unsupervised pre-training followed by supervised refinement yields the best overall accuracy.