What is the Appropriate Index Formula to Estimate

What is the Appropriate Index Formula to Estimate Producer Price Change? December 11, 2020 Robert Martin Jonathan Weinhagen 1 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

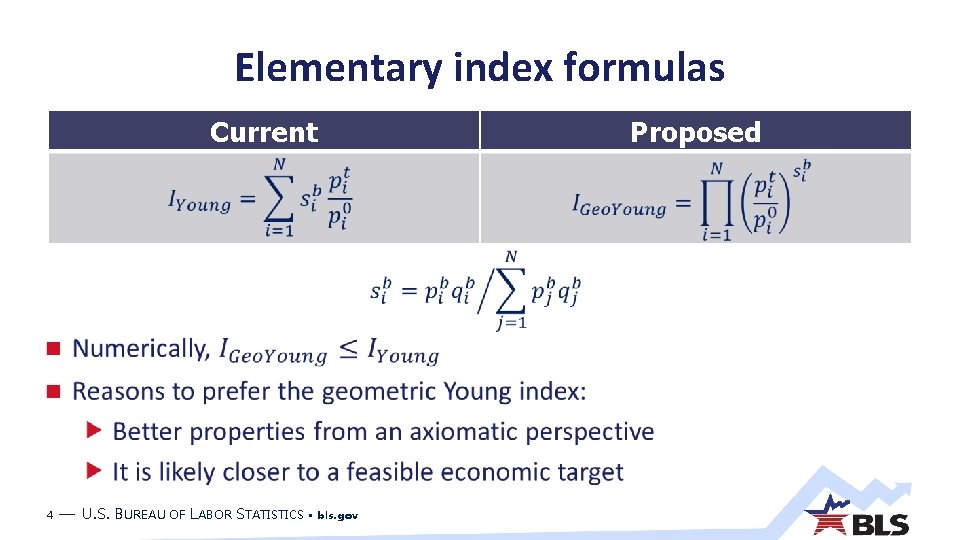
Summary PPI currently uses a modified Laspeyres formula for all indexes Industry Commodity Final Demand - Intermediate Demand (FD-ID) Net inputs to industry Specifically, the Young formula is used at the elementary level We are proposing using the geometric Young for elementary indexes 2 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

Background In the 1990 s, the Consumer Price index switched from a modified Laspeyres to a weighted geometric mean for most elementary-level price indexes PPI chose not to make this change because the Laspeyres index is a lower bound for a certain theoretical output price index Mathematically, a geometric mean index will be less than or equal to a Laspeyres index However, other axiomatic and economic arguments are more favorable to the geometric mean 3 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

Elementary index formulas Current 4 — U. S. BUREAU OF LABOR STATISTICS • bls. gov Proposed

Axiomatic factors Time-reversal test “…the same result should be obtained…whether the change is measured forward in time, from 0 to t, or backward in time, from t to 0. ” IMF, 2004 – Young – Geometric Young The Young index’s failure is interpreted as an upward bias 5 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

Axiomatic factors (continued) Transitivity (or circularity) test: “The chained index between two periods should equal the direct index between the same two periods. ” – IMF, 2004 – Young – Geometric Young Does not necessarily imply direction of bias The axiomatic approach favors the geometric Young index also has upward “formula bias” when prices bounce (Reinsdorf, 1998) 6 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

Economic approach to output price indexes The Laspeyres index is a lower bound to theoretical Fixed- Input Output Price Index (FIOPI) based on reference period technology and inputs FIOPI: Measures the revenue change if inputs and technology were fixed between periods (i. e. , if firms could only adjust their mix of outputs in response to relative price changes) Different theoretical FIOPI exist for different productive capacities (levels of inputs and technology) In general, they are impractical to estimate 7 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

Economic approach (continued) 8 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

Simulations with PPI microdata We calculate monthly elementary-level indexes using: Current formula (Young) Proposed formula (Geometric Young) These are aggregated to create higher-level indexes (6 -digit commodity, 6 -digit industry, and FD-ID indexes) Upper level aggregation uses current modified Laspeyres (Lowe) methodology This presentation focuses on 6 -digit commodity and FD indexes 9 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

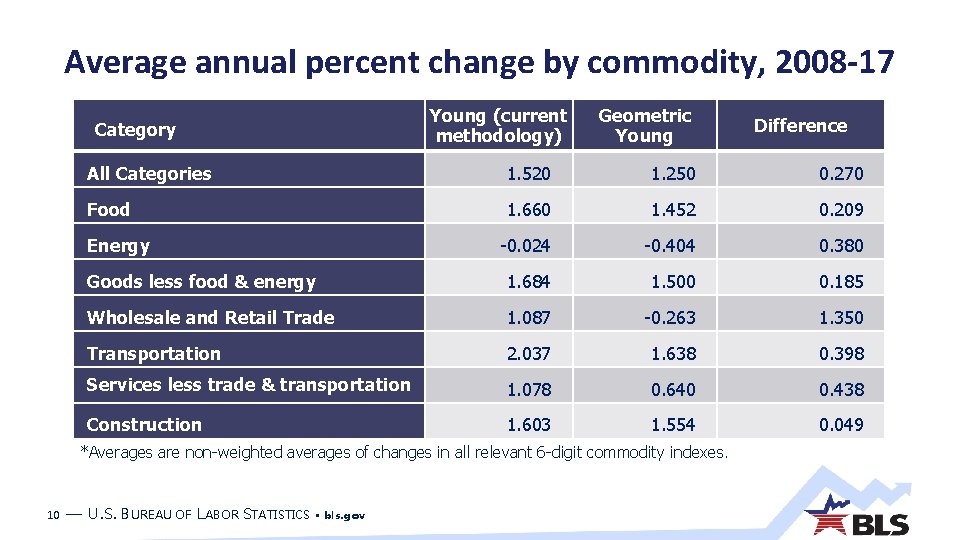
Average annual percent change by commodity, 2008 -17 Young (current methodology) Category Geometric Young All Categories 1. 520 1. 250 0. 270 Food 1. 660 1. 452 0. 209 -0. 024 -0. 404 0. 380 Goods less food & energy 1. 684 1. 500 0. 185 Wholesale and Retail Trade 1. 087 -0. 263 1. 350 Transportation 2. 037 1. 638 0. 398 Services less trade & transportation 1. 078 0. 640 0. 438 Construction 1. 603 1. 554 0. 049 Energy *Averages are non-weighted averages of changes in all relevant 6 -digit commodity indexes. 10 Difference — U. S. BUREAU OF LABOR STATISTICS • bls. gov

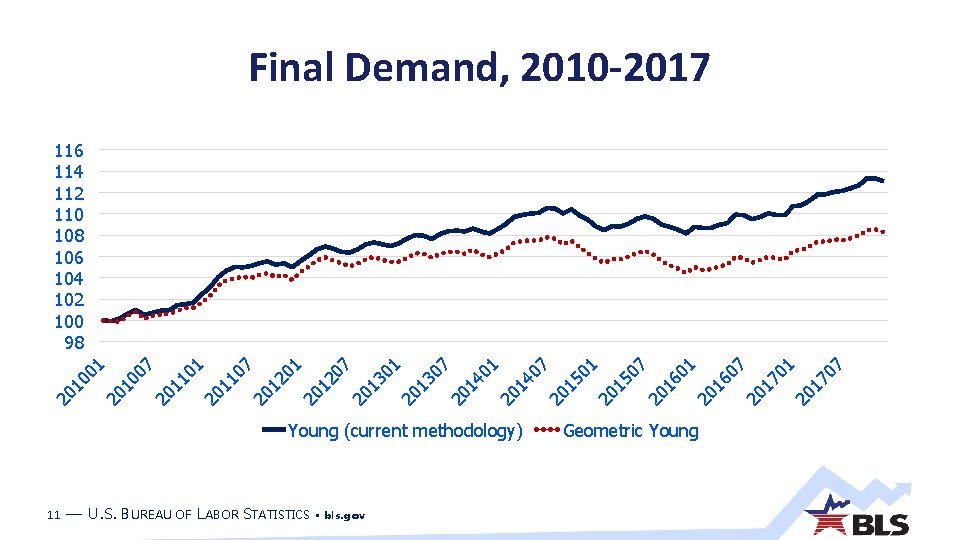
Final Demand, 2010 -2017 Young (current methodology) 11 — U. S. BUREAU OF LABOR STATISTICS • bls. gov Geometric Young 07 20 17 01 20 17 07 20 16 01 20 16 07 20 15 01 20 15 07 20 14 01 20 14 07 20 13 01 20 13 07 20 12 01 20 12 07 20 11 01 20 11 07 20 10 01 116 114 112 110 108 106 104 102 100 98

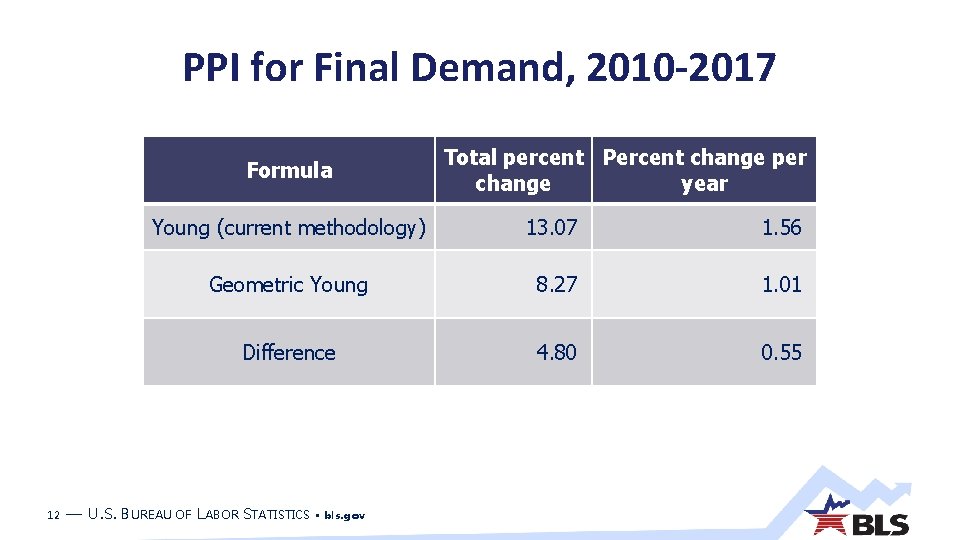
PPI for Final Demand, 2010 -2017 Formula 12 Total percent Percent change per change year Young (current methodology) 13. 07 1. 56 Geometric Young 8. 27 1. 01 Difference 4. 80 0. 55 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

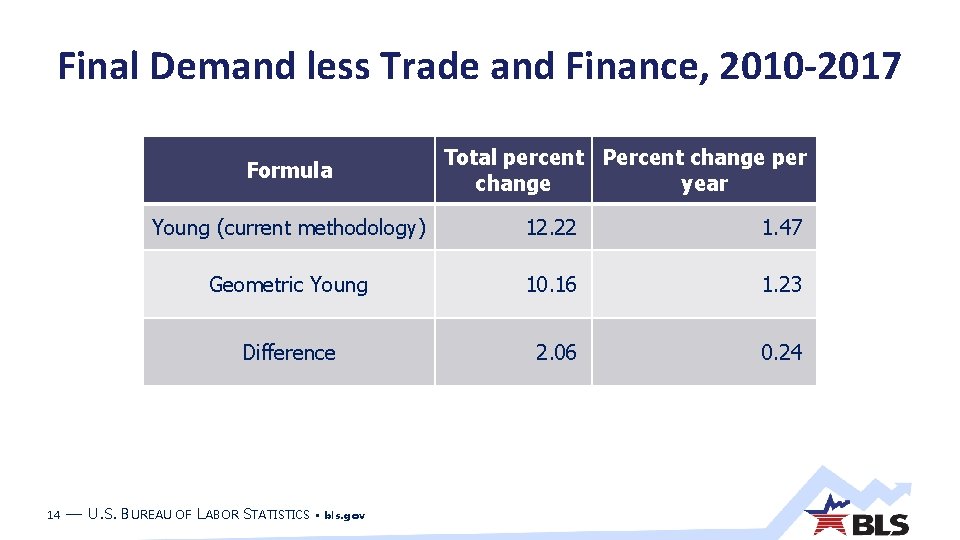
Final Demand less Trade and Finance, 2010 -2017 Young (current methodology) 13 — U. S. BUREAU OF LABOR STATISTICS • bls. gov Geometric Young 07 20 17 01 20 17 07 20 16 01 20 16 07 20 15 01 20 15 07 20 14 01 20 14 07 20 13 01 20 13 07 20 12 01 20 12 07 20 11 01 20 11 07 20 10 01 116 114 112 110 108 106 104 102 100 98

Final Demand less Trade and Finance, 2010 -2017 Formula 14 Total percent Percent change per change year Young (current methodology) 12. 22 1. 47 Geometric Young 10. 16 1. 23 Difference 2. 06 0. 24 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

A closer look at margin prices Ignoring Trade and Finance, formula differences line up with estimates for CPI data (e. g. , Boskin 1996) Trade and Finance PPIs are based in part on gross margins Margin prices tend to exhibit Higher dispersion in general More extreme values Greater dispersion leads to greater formula differences 15 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

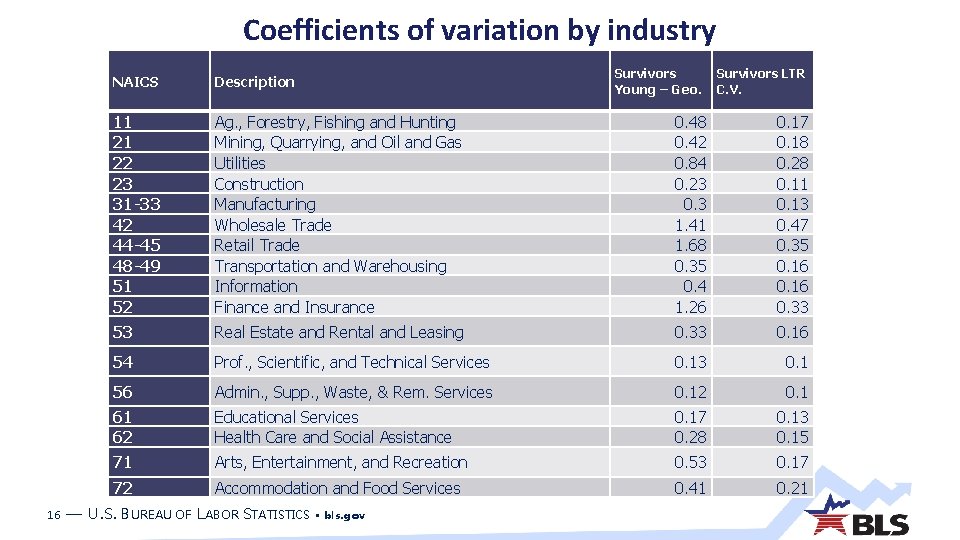
Coefficients of variation by industry 16 Survivors Young – Geo. Survivors LTR C. V. NAICS Description 11 21 22 23 31 -33 42 44 -45 48 -49 51 52 Ag. , Forestry, Fishing and Hunting Mining, Quarrying, and Oil and Gas Utilities Construction Manufacturing Wholesale Trade Retail Trade Transportation and Warehousing Information Finance and Insurance 0. 48 0. 42 0. 84 0. 23 0. 3 1. 41 1. 68 0. 35 0. 4 1. 26 0. 17 0. 18 0. 28 0. 11 0. 13 0. 47 0. 35 0. 16 0. 33 53 Real Estate and Rental and Leasing 0. 33 0. 16 54 Prof. , Scientific, and Technical Services 0. 13 0. 1 56 Admin. , Supp. , Waste, & Rem. Services 0. 12 0. 1 61 62 Educational Services Health Care and Social Assistance 0. 17 0. 28 0. 13 0. 15 71 Arts, Entertainment, and Recreation 0. 53 0. 17 72 Accommodation and Food Services 0. 41 0. 21 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

Extreme values and geometric means Dispersion is a concern if it is driven by extreme values Compared to an arithmetic mean, a geometric mean is: Less sensitive to large extreme values (price relatives) More sensitive to small (i. e. , close to zero) extreme values Despite superior axiomatic and economic properties, the geometric Young may perform poorly when there are price relatives close to zero Meaning it may not reflect the central tendency of the elementary cell 17 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

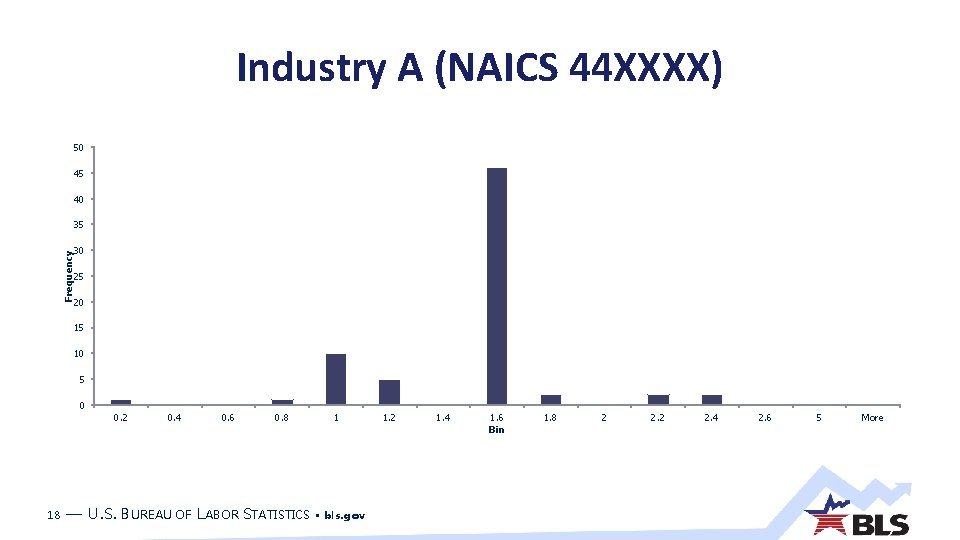
Industry A (NAICS 44 XXXX) 50 45 40 35 Frequency 30 25 20 15 10 5 0 0. 2 18 0. 4 0. 6 0. 8 — U. S. BUREAU OF LABOR STATISTICS 1 • bls. gov 1. 2 1. 4 1. 6 Bin 1. 8 2 2. 4 2. 6 5 More

Industry A (NAICS 44 XXXX) From December 2007 to December 2008 Young index increased 52. 3 percent Geometric Young index increased 25. 3 percent Difference of 26. 9 percentage points Excluding the lowest and highest relatives: Young index increased 61. 4 percent Geometric Young index increased 57. 7% Difference is only 3. 7 percentage points 19 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

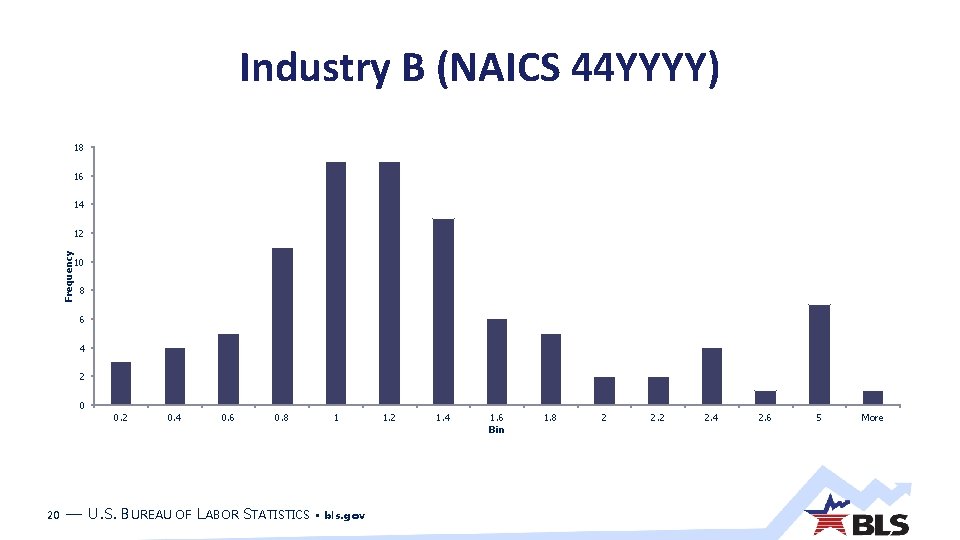
Industry B (NAICS 44 YYYY) 18 16 14 Frequency 12 10 8 6 4 2 0 0. 2 20 0. 4 0. 6 0. 8 — U. S. BUREAU OF LABOR STATISTICS 1 • bls. gov 1. 2 1. 4 1. 6 Bin 1. 8 2 2. 4 2. 6 5 More

Industry B (NAICS 44 YYYY) From December 2007 to June 2014 Young index increased 14. 1 percent Geometric Young index fell 9. 1 percent Difference of 23. 2 percentage points Excluding the lowest and highest relatives, the difference is 19. 4 percentage points (+11. 2% versus -8. 1%) Excluding the top five highest and lowest relatives, the difference is 14. 6 percentage points (+16% vs. +1. 4%) 21 — U. S. BUREAU OF LABOR STATISTICS • bls. gov still

Implications formula choice We examined the 20 industry/cycles with the largest formula differences. For about 75 percent, general dispersion seems to drive the differences rather than extreme values We then repeated the full index simulations with bounds of 0. 05 and 20 on the monthly relatives Average Trade index gaps decrease by only 0. 015 percentage points per year. Bounds of 0. 25 and 4 decrease average gap by add’l 0. 026 Extreme values do not appear to explain much of the formula differences 22 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

Summary and recommendations We propose adopting a geometric Young formula for all elementary PPI This would resolve axiomatic and numerical issues with the current Young formula The geometric Young index may be closer to a feasible economic target (the FIOPI based on intermediate inputs and technology) Extreme margin changes do not appear to be driving results 23 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

Contact Information Jonathan Weinhagen Senior Economist Producer Price Index Program www. bls. gov/ppi 202 -691 -7709 weinhagen. jonathan@bls. gov 24 — U. S. BUREAU OF LABOR STATISTICS • bls. gov

References IMF/ILO/OECD/Eurostat/UNECE/World Bank. 2004. Producer Price Index Manual: Theory and Practice. Edited by P. Armknecht. Washington, DC: International Monetary Fund. https: //www. imf. org/external/pubs/ft/ppi/2010/manual/ppi. pdf. Reinsdorf, Marshall B. 1998. "Formula Bias and Within-Stratum Substitution Bias in the U. S. CPI. " The Review of Economics and Statistics (MIT Press) 80 (2): 175 -187. doi: 10. 1162/003465398557375. Diewert, W. Erwin. 1983. "The Theory of the Output Price Index and the Measurement of Real Output Change. " In Price Level Measurement, edited by W. Erwin and C. Montmarquette Diewert, 1049 -1113. Ottawa: Statistics Canada. 25 — U. S. BUREAU OF LABOR STATISTICS • bls. gov