What is RSA RSA is a system employed

What is RSA • RSA is a system employed to create the encrypted message in which the key used for encryption is different from that used to decrypt. • It is employed in all situations that require security, such as the use of cash payments, in passwords of e-mail, in digital encryption and is the most well-known algorithm for asymmetric encryption.

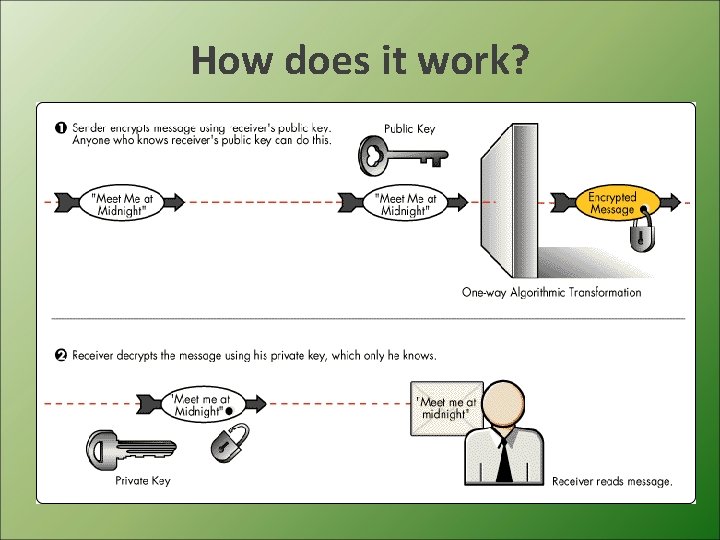
How does it work?

Why RSA was created? The RSA system has been created to answer to the necessity of a stringent security in today's society. In previous encryption methods, in fact, there were the "pass key" between the sender and the receiver of the message. The RSA system, however, uses two keys: a public key and a private key to decrypt

The creation of RSA The researchers then began looking for a one-way mathematical function (a function which tends to be difficult invertible) in the arithmetic clock and also the mathematicians studied the inverse operations, the multiplication of two numbers and their factorization.

The inventors The aim was reached by three U. S. researchers at MIT in 1977, Adi Shamir, Ron Rivest, Leonard Adleman.

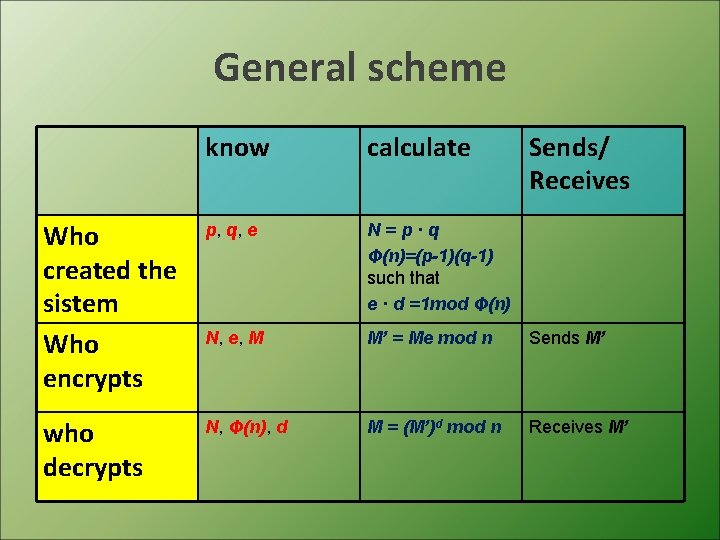
System numbers of RSA • p and q, two prime numbers • n, product of p and q • Φ (n) = (p-1) (q-1) • e, public key divisor of Φ (n) • d, secret key such that e · d = 1 mod Φ (n) • M, plaintext message • M’, encrypted message

How can you create a RSA system? • • choose two prime numbers, p and q calculate n = p · q calculate Φ (n) = (p-1) (q-1) calculate e and d such that e · d = 1 modΦ (n)

How can you apply the RSA system? Ø To encrypt: • consider the message M • calculate M’= Me • M’ is the encrypted message Ø To decrypt: • consider the message M’ • calculate M = (M’)d • M is the decrypted message

General scheme know calculate Sends/ Receives Who created the sistem Who encrypts p, q, e N=p·q Φ(n)=(p-1)(q-1) such that e · d =1 mod Φ(n) N, e, M M’ = Me mod n Sends M’ who decrypts N, Φ(n), d M = (M’)d mod n Receives M’

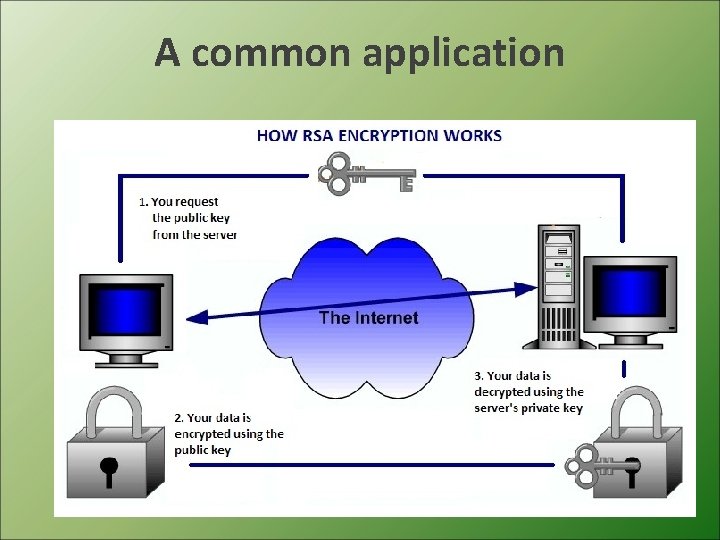
A common application