What is quantum in quantum randomness Alexia Auffves


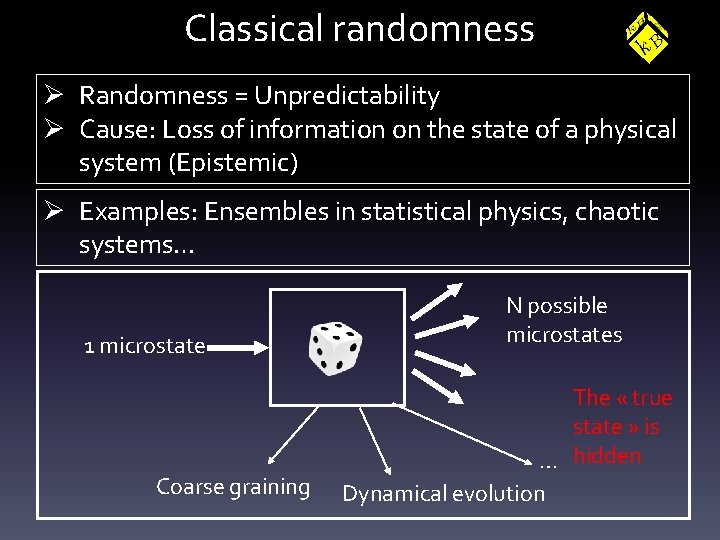






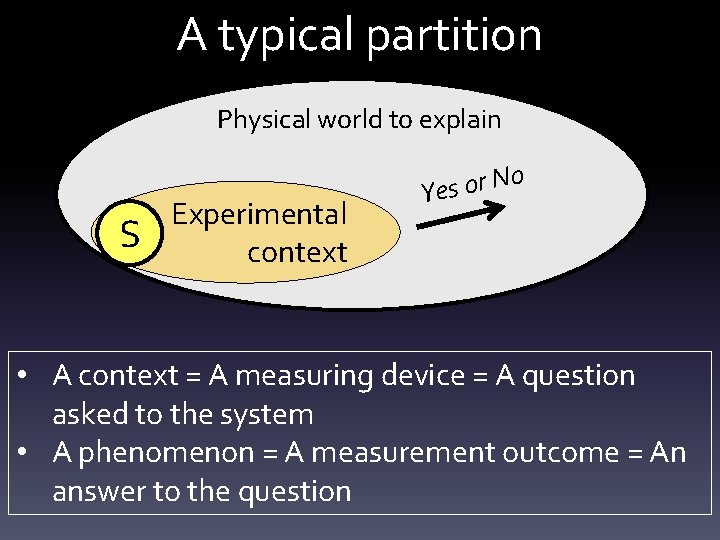






















![Step 2: Call ontology for help Pvj|ui = Tr[P’i RP’’j. R] Depends on Cu Step 2: Call ontology for help Pvj|ui = Tr[P’i RP’’j. R] Depends on Cu](https://slidetodoc.com/presentation_image_h/110b3abfa44ef8bd902a8c177d889c4b/image-70.jpg)
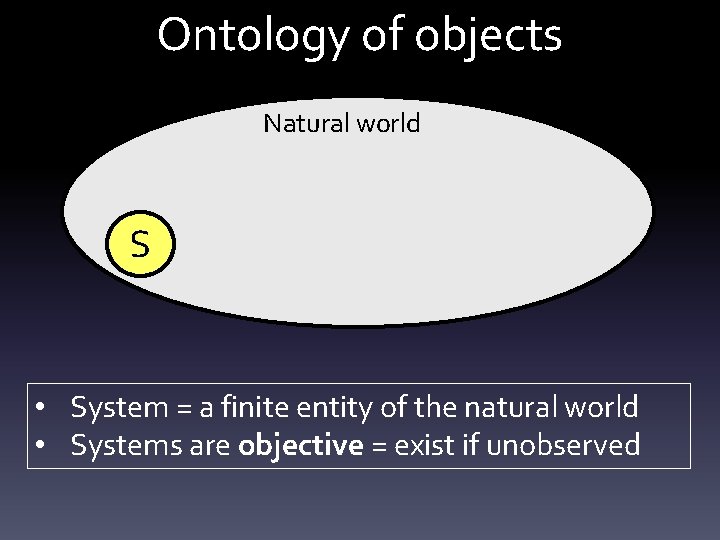
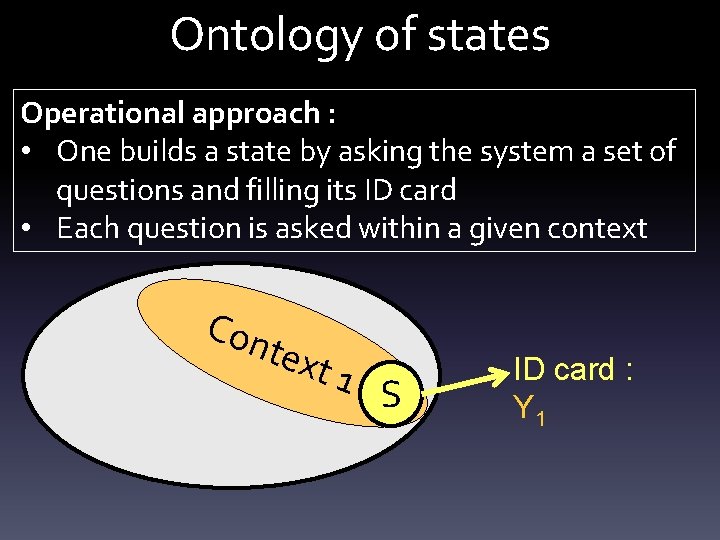
![Step 3: Chase the contradiction Wanted: R(Ui, Vj) • • • Tr[R 2 P’k]=N Step 3: Chase the contradiction Wanted: R(Ui, Vj) • • • Tr[R 2 P’k]=N](https://slidetodoc.com/presentation_image_h/110b3abfa44ef8bd902a8c177d889c4b/image-71.jpg)
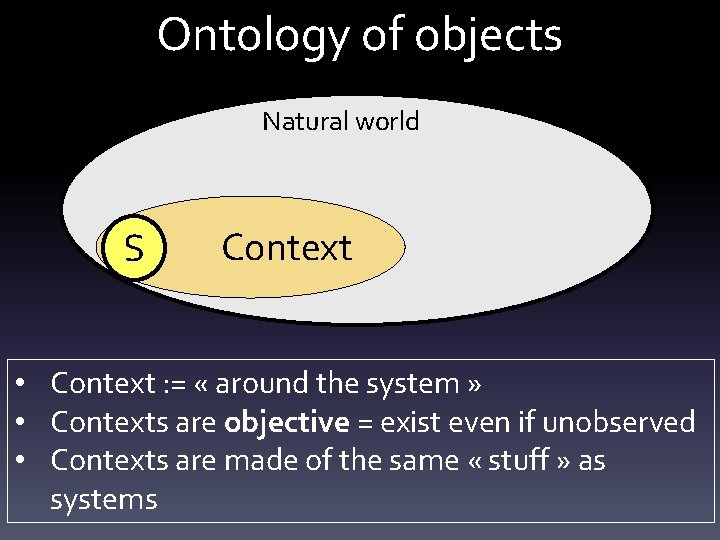
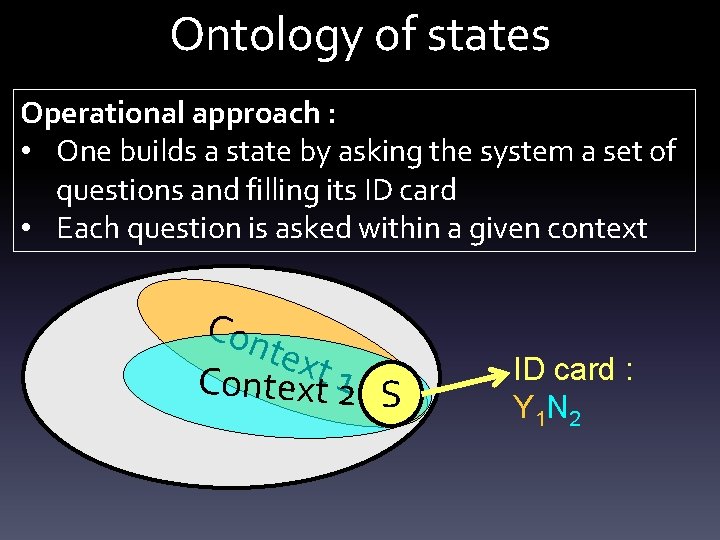
![Step 4: Unitary matrices Pvj|ui = Tr[Pi Σ+PjΣ] Σ = [Pvj|ui 1/2 exp(iφvj|ui) ] Step 4: Unitary matrices Pvj|ui = Tr[Pi Σ+PjΣ] Σ = [Pvj|ui 1/2 exp(iφvj|ui) ]](https://slidetodoc.com/presentation_image_h/110b3abfa44ef8bd902a8c177d889c4b/image-72.jpg)
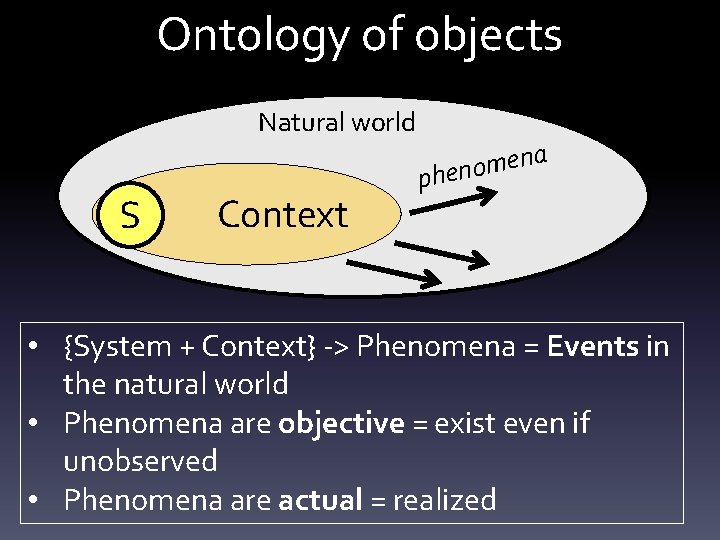
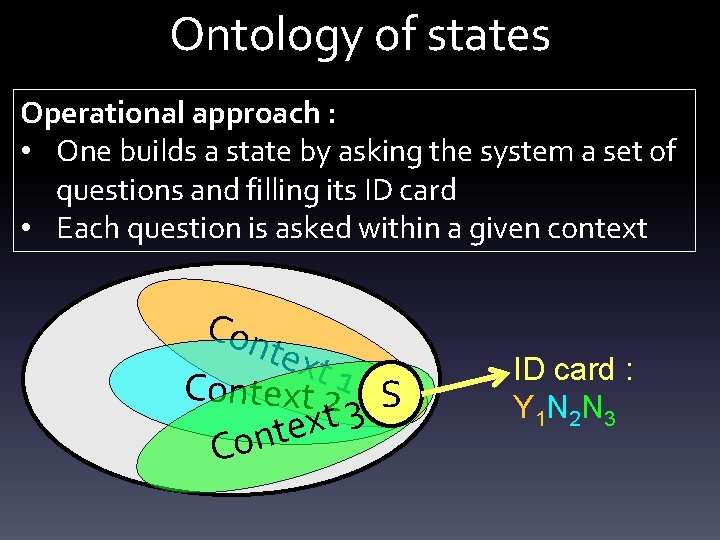
![And finally: Usual quantum formalism • Pvj|ui = Tr[Pi Σv|u+PjΣv|u] • Pvj|ui = Tr[Σv|u. And finally: Usual quantum formalism • Pvj|ui = Tr[Pi Σv|u+PjΣv|u] • Pvj|ui = Tr[Σv|u.](https://slidetodoc.com/presentation_image_h/110b3abfa44ef8bd902a8c177d889c4b/image-73.jpg)
- Slides: 73

What is quantum in quantum randomness? Alexia Auffèves Institut Néel, CNRS & Université Grenoble Alpes P. Grangier (I. Optique), N. Farouki (CEA Grenoble) Concepts of probabilities in the Sciences ESI, 29 -30 October, Vienna, Austria

Context • Yesterday’s talks: About subjective/objective probabilities + mathematical properties NO Pics from S. Zabell’s talk • Today we shall consider the precursor of probabilities = Randomness and its causes => No mathematical formalism • Focus on physical theories built on randomness

Classical randomness Ø Randomness = Unpredictability Ø Cause: Loss of information on the state of a physical system (Epistemic) Ø Examples: Ensembles in statistical physics, chaotic systems… 1 microstate Coarse graining N possible microstates The « true state » is … hidden Dynamical evolution

Quantum randomness? Ø Naïve early interpretation: Heisenberg microscope Ø Randomness due to interaction of a microscopic object with the macroscopic experimental context Ø The system has a hidden state Ø The state is perturbed by the measurement Ø Irreducible coarse-graining Ø Quantum randomness looks very classical!

Quantum randomness? Ø 2 fundamental quantum features: 1. Contextuality: Phenomena depend on the state of the (experimental) context around the system => Philosophical position: Contextual objectivity 2. Quantization: Experimental signals are discrete 1. How to think quantum randomness in a contextual world? Challenge: Intuitions on randomness are non-contextual 2. Can we relate quantum randomness and quantization? What is quantum in quantum randomness?

Outline • A new ontology for quantum mechanics: The « CSM » approach • Randomness in a contextual world • Quantum physics vs thermodynamics

Outline • A new ontology for quantum mechanics: The « CSM » approach • Randomness in a contextual world • Quantum physics vs thermodynamics Ontology: What is, by opposition of what we can know (epistemology)

1 philosopher + 2 physicists • Our motivation: Introduction of the « quantum stuff » with words and concepts • Our philosophical position: Realist and objectivist (there is a world that exists out there, and we can know it)

Our methodology Knowing that • Ontology is never demonstrated, but postulated • Postulates are (often) based on intuitions • Intuitions are (always) based on custom We shall • Deconstruct classical intuitions (based on classical phenomenology) • Rebuild a new ontology, by induction from quantum phenomenology

Ontology of objects Natural world S • System = a finite entity of the natural world • Systems are objective = exist if unobserved

Ontology of objects Natural world S Context • Context : = « around the system » • Contexts are objective = exist even if unobserved • Contexts are made of the same « stuff » as systems

Ontology of objects Natural world S Context a n e m heno p • {System + Context} -> Phenomena = Events in the natural world • Phenomena are objective = exist even if unobserved • Phenomena are actual = realized

A typical partition Physical world to explain S Experimental context o N r o s Ye • A context = A measuring device = A question asked to the system • A phenomenon = A measurement outcome = An answer to the question

Ontology of states Operational approach : • One builds a state by asking the system a set of questions and filling its ID card • Each question is asked within a given context Con text 1 S ID card : Y 1

Ontology of states Operational approach : • One builds a state by asking the system a set of questions and filling its ID card • Each question is asked within a given context Context 12 S ID card : Y 1 N 2

Ontology of states Operational approach : • One builds a state by asking the system a set of questions and filling its ID card • Each question is asked within a given context Context 2 1 S 3 t x e t n Co ID card : Y 1 N 2 N 3

Classical phenomenology I can obtain repeatably the same answers to the same questions S 3 t x e t n Co ID card : Y 1 N 2 N 3

Classical phenomenology I can obtain repeatably the same answers to the same questions Context 2 S ID card : Y 1 N 2 N 3

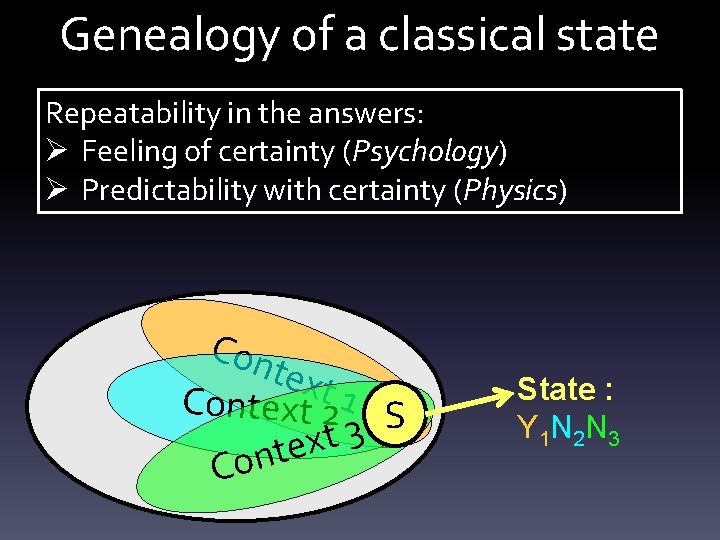
Genealogy of a classical state Repeatability in the answers: Ø Feeling of certainty (Psychology) Ø Predictability with certainty (Physics) Con text Context 2 1 S 3 t x e t n Co State : Y 1 N 2 N 3

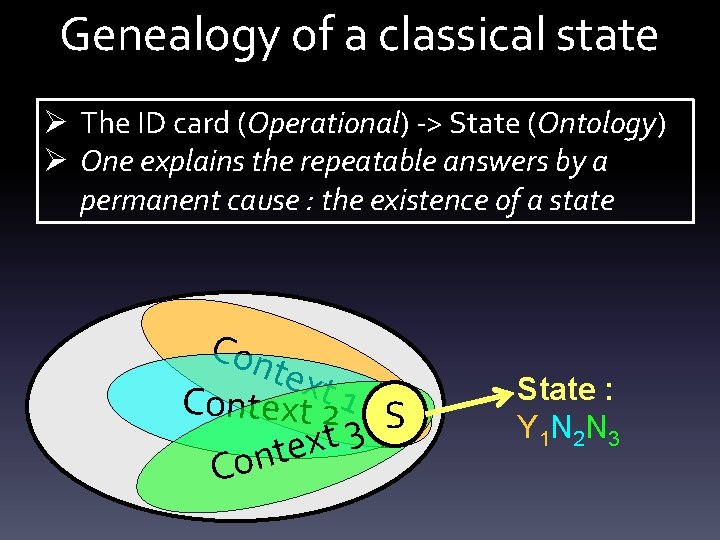
Genealogy of a classical state Ø The ID card (Operational) -> State (Ontology) Ø One explains the repeatable answers by a permanent cause : the existence of a state Con text Context 2 1 S 3 t x e t n Co State : Y 1 N 2 N 3

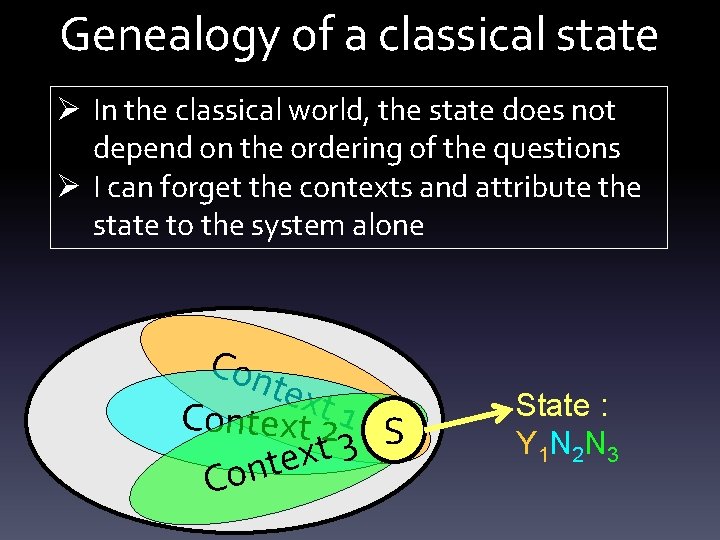
Genealogy of a classical state Ø In the classical world, the state does not depend on the ordering of the questions Ø I can forget the contexts and attribute the state to the system alone Con text Context 2 1 S 3 t x e t n Co State : Y 1 N 2 N 3

Genealogy of a classical state Ø In the classical world, the state does not depend on the ordering of the questions : Ø I can forget the contexts and attribute the state to the system alone Ø Non contextual state S State : Y 1 N 2 N 3

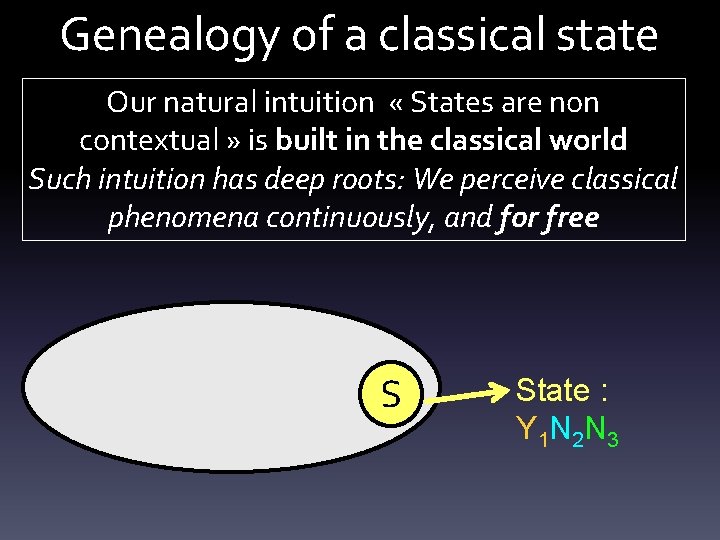
Genealogy of a classical state Our natural intuition « States are non contextual » is built in the classical world Such intuition has deep roots: We perceive classical phenomena continuously, and for free S State : Y 1 N 2 N 3

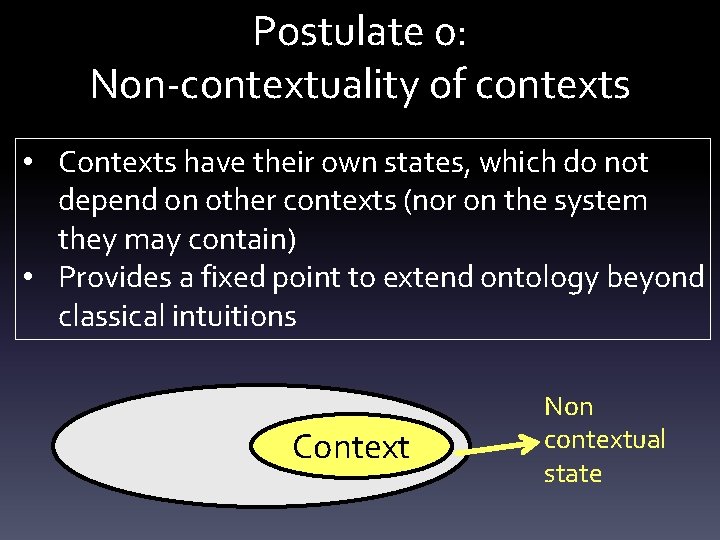
Postulate 0: Non-contextuality of contexts • Contexts have their own states, which do not depend on other contexts (nor on the system they may contain) • Provides a fixed point to extend ontology beyond classical intuitions Context Non contextual state

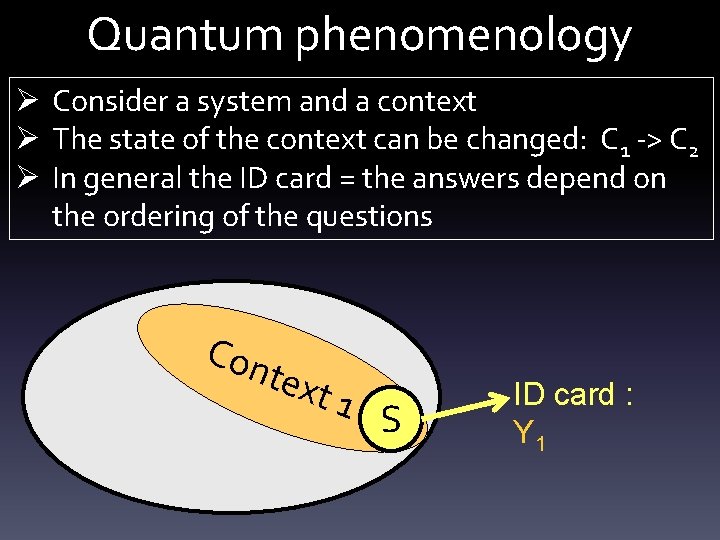
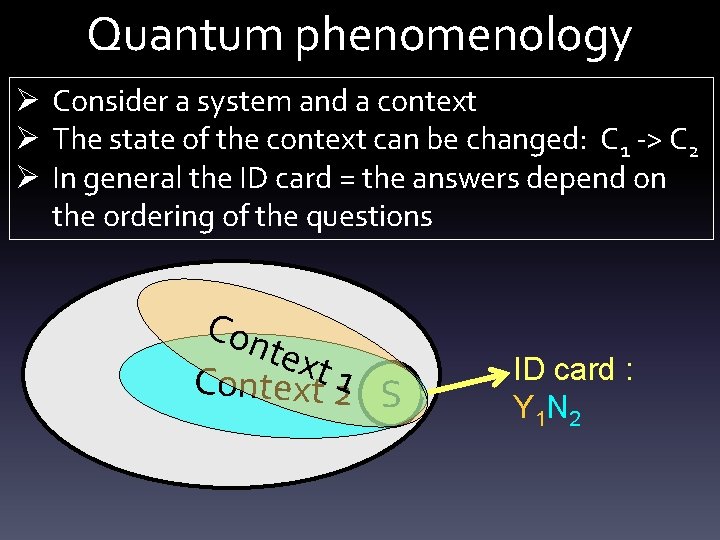
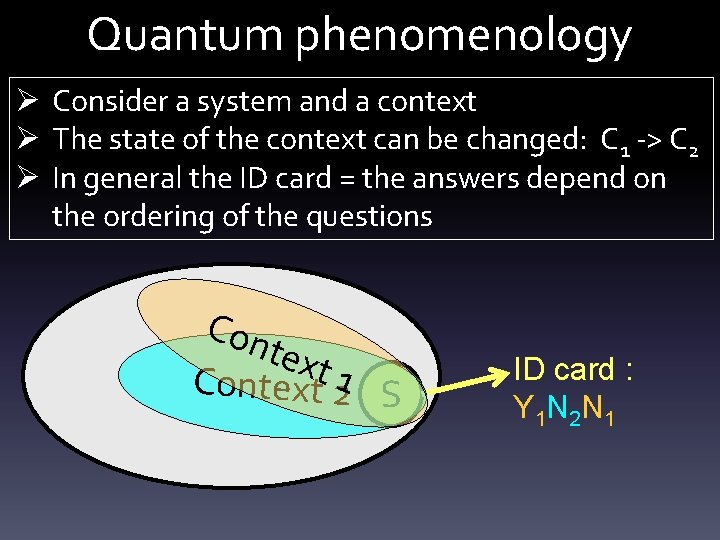
Quantum phenomenology Ø Consider a system and a context Ø The state of the context can be changed: C 1 -> C 2 Ø In general the ID card = the answers depend on the ordering of the questions Con text 1 S ID card : Y 1

Quantum phenomenology Ø Consider a system and a context Ø The state of the context can be changed: C 1 -> C 2 Ø In general the ID card = the answers depend on the ordering of the questions Con text Context 21 S ID card : Y 1 N 2

Quantum phenomenology Ø Consider a system and a context Ø The state of the context can be changed: C 1 -> C 2 Ø In general the ID card = the answers depend on the ordering of the questions Con text Context 21 S ID card : Y 1 N 2 N 1

Example: Single photon • System: Single photon • Context: Polarizing Beam Splitter (PBS) • Question 1= PBS: {H, V} V H S Ø Transmitted

Example: Single photon • • System: Single photon Context: Polarizing Beam Splitter (PBS) Question 1= PBS: {H, V} Question 2= PBS: {D, A} V H D A V H S Ø Tr Ø Reflected

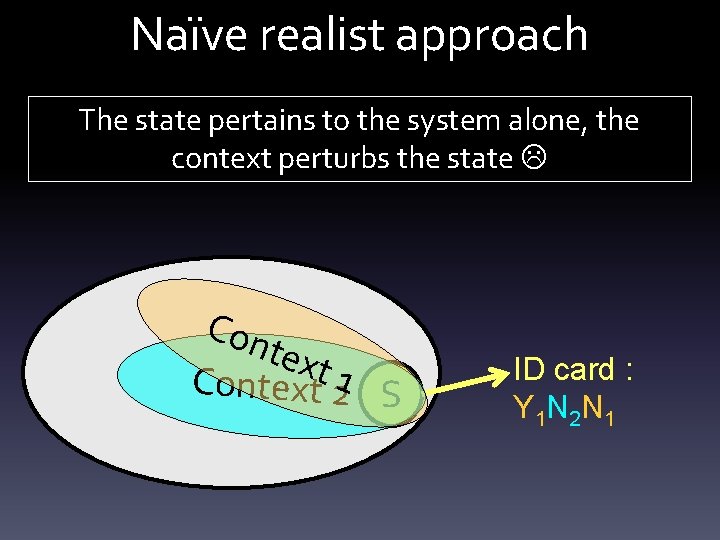
Naïve realist approach The state pertains to the system alone, the context perturbs the state Con text Context 21 S ID card : Y 1 N 2 N 1

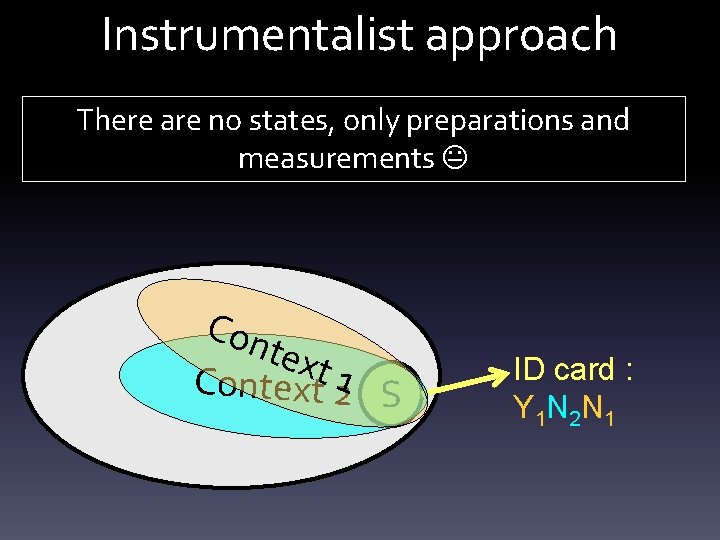
Instrumentalist approach There are no states, only preparations and measurements Con text Context 21 S ID card : Y 1 N 2 N 1

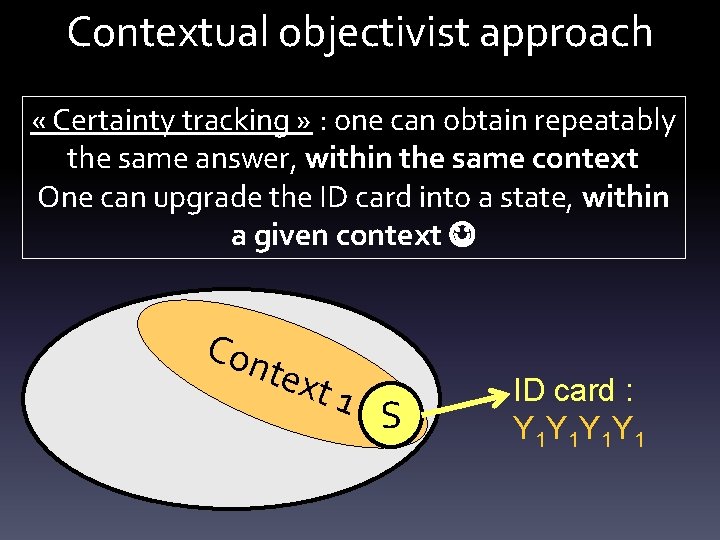
Contextual objectivist approach « Certainty tracking » : one can obtain repeatably the same answer, within the same context One can upgrade the ID card into a state, within a given context Con text 1 S ID card : Y 1 Y 1

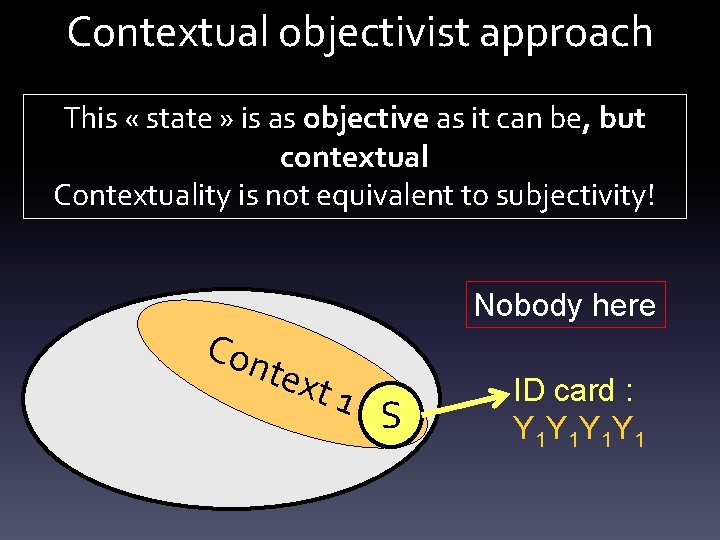
Contextual objectivist approach This « state » is as objective as it can be, but contextual Contextuality is not equivalent to subjectivity! Con Nobody here text 1 S ID card : Y 1 Y 1

Postulate 1 : C-S-M Ø Ø A « state » labels both a system and a context A contextual state is further called a modality Modalities are as objective as classical states Contextual objectivity • Within a given context, modalities are mutually exclusive • Two modalities pertaining to two different contexts are not necessarily exclusive Auffèves and Grangier, Foundations of Physics 46: 121– 137 (2016) Grangier & Auffe ves, 2018 What is quantum in quantum randomness? Phil. Trans. R. Soc. A 376: 20170322.

Postulate 2 : Elementary systems are characterized by a fixed, discrete number N of exclusive modalities (Quantization/ « Discreteness » of modalities) N is independant of the context. A critical- and textbook - partition of the world : A context around an elementary system with N exclusive modalities M 1 C S M 2 M N

Example: single photon • Context : A PBS with neutral axes {H, V}. • Modality : « transmitted » or « reflected » V H V H S • A photon has no state by itself => A photon + polarizer have, and it is a modality. • A « coherent superposition » is a modality in another contexts: |H>+|V> = |D>

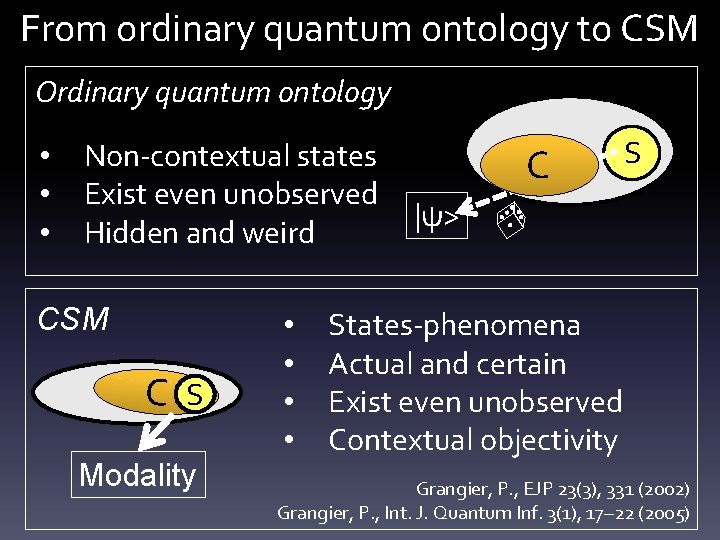
From ordinary quantum ontology to CSM Ordinary quantum ontology • • • Non-contextual states Exist even unobserved |ψ> Hidden and weird CSM C S Modality • • C S States-phenomena Actual and certain Exist even unobserved Contextual objectivity Grangier, P. , EJP 23(3), 331 (2002) Grangier, P. , Int. J. Quantum Inf. 3(1), 17– 22 (2005)

Outline • A new ontology for quantum mechanics: The « CSM » approach • Randomness in a contextual world • Quantum physics vs thermodynamics

Motivation Relate randomness, contextuality and quantization Challenge: Randomness in the classical world presupposes that systems have states Considered partition of the world : A context around an elementary system with N exclusive modalities M 1 C S M 2 M N

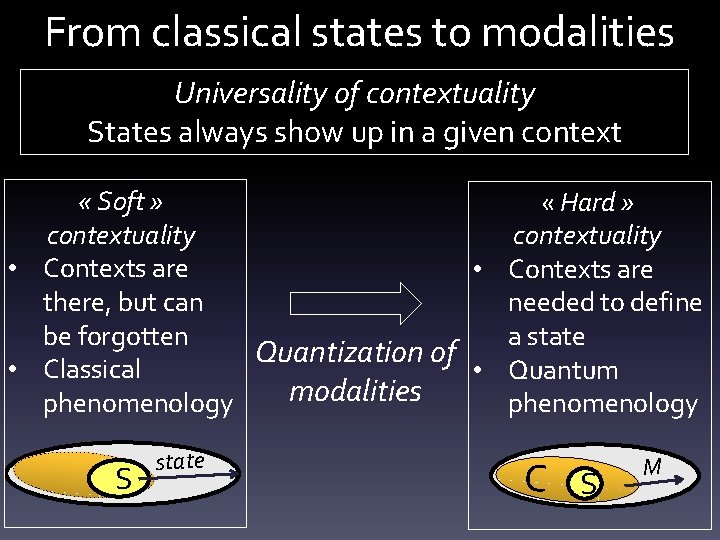
From classical states to modalities Universality of contextuality States always show up in a given context « Soft » « Hard » contextuality • Contexts are there, but can needed to define be forgotten a state Quantization of • Classical • Quantum modalities phenomenology S state C S M

Claim Ø Universality of contextuality Ø Discreteness of modalities for elementary systems « Hard contextuality » Ø Non commutation of the questions Ø Unpredictability of the answer as the context changes Ø Ontological randomness

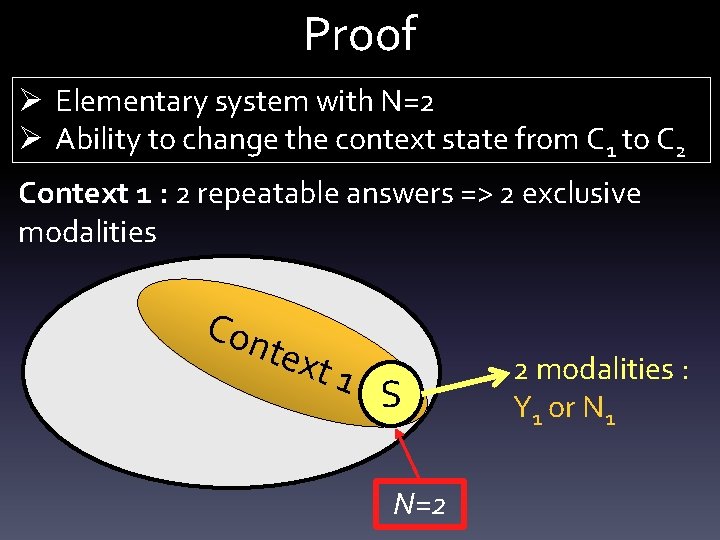
Proof Ø Elementary system with N=2 Ø Ability to change the context state from C 1 to C 2 Context 1 : 2 repeatable answers => 2 exclusive modalities Con text 1 S N=2 2 modalities : Y 1 or N 1

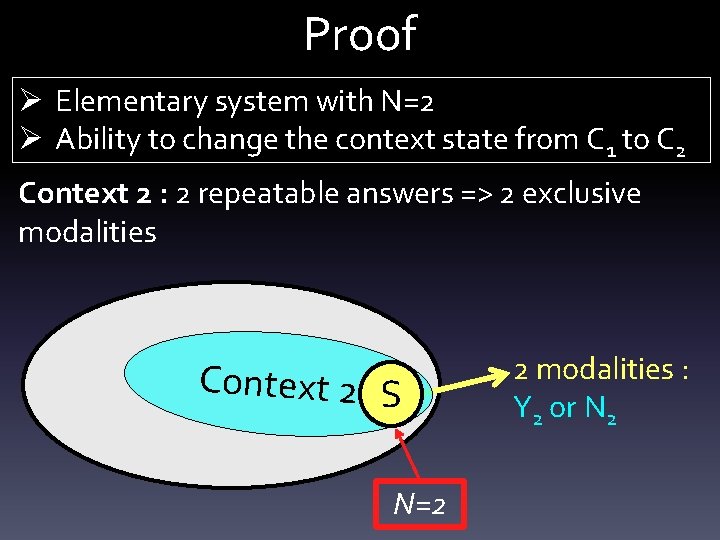
Proof Ø Elementary system with N=2 Ø Ability to change the context state from C 1 to C 2 Context 2 : 2 repeatable answers => 2 exclusive modalities Context 2 S N=2 2 modalities : Y 2 or N 2

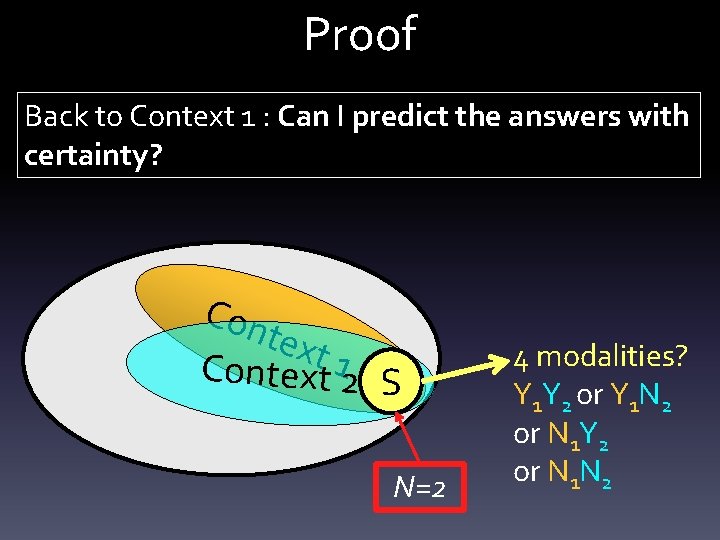
Proof Back to Context 1 : Can I predict the answers with certainty? Con text Context 12 S N=2 4 modalities? Y 1 Y 2 or Y 1 N 2 or N 1 Y 2 or N 1 N 2

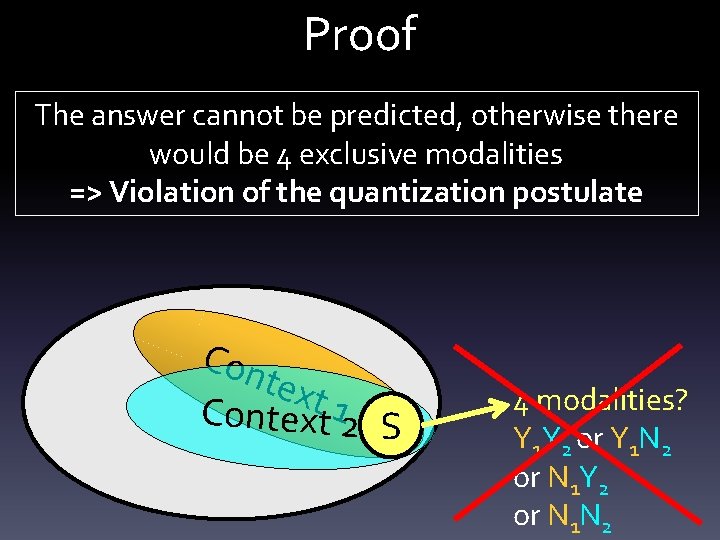
Proof The answer cannot be predicted, otherwise there would be 4 exclusive modalities => Violation of the quantization postulate Con text Context 1 2 S 4 modalities? Y 1 Y 2 or Y 1 N 2 or N 1 Y 2 or N 1 N 2

Ontological randomness Ø Universal contextuality Ø System with discrete modalities Ø Ability to change the context state Conflict: Less certain answers allowed, than possible answers to possible questions • Non-commutation of the questions • Unpredictable answers • Ontological randomness Core quantum features

Towards quantum randomness Ø Universal contextuality Ø System with discrete modalities Ø Ability to change the context state continuously To be described: random change of modality Ø Quantum randomness (Born’s rule) Ø Hard contextuality Ø Quantum formalism: Hilbert spaces, unitary transformations and Born’s rule Auffèves & Grangier, Scientific Reports 43365 (2017)

Outline • A new ontology for quantum mechanics: the « CSM » approach • Randomness in a contextual world • Quantum physics vs thermodynamics

Context and motivation «Classical thermodynamics » = • Statistical physics (XIXth century) • Stochastic thermodynamics (XXth) are based on probabilities & randomness Ø These theories have inspired concepts and research programs in quantum mechanics Ø Was the transposition fruitful? ? ?

Statistical physics Systems = large amounts of particles + degrees of freedom The real state = the micro-state (hidden, below) • Emergence of the macroscopic world by « coarse graining » the microscopic world • Avering probabilities due to epistemic randomness • Reductionist program

Zurek’s program for quantum mechanics Assumption: Schrödinger equation > Measurement postulate Goal: Emergence of the classical from the quantum without needing the measurement postulate

CSM and the classical-quantum boundary • Context around a system • Reduce the number of modalities of the system ---- Elementary system

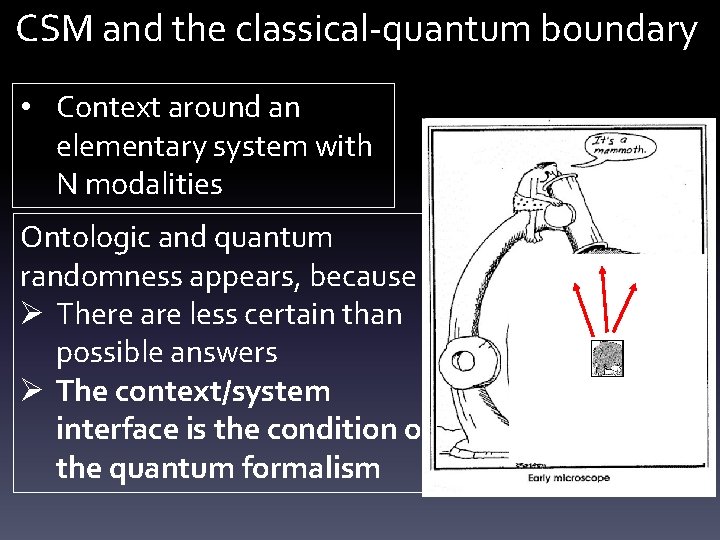
CSM and the classical-quantum boundary • Context around an elementary system with N modalities Ontologic and quantum randomness appears, because Ø There are less certain than possible answers Ø The context/system interface is the condition of the quantum formalism

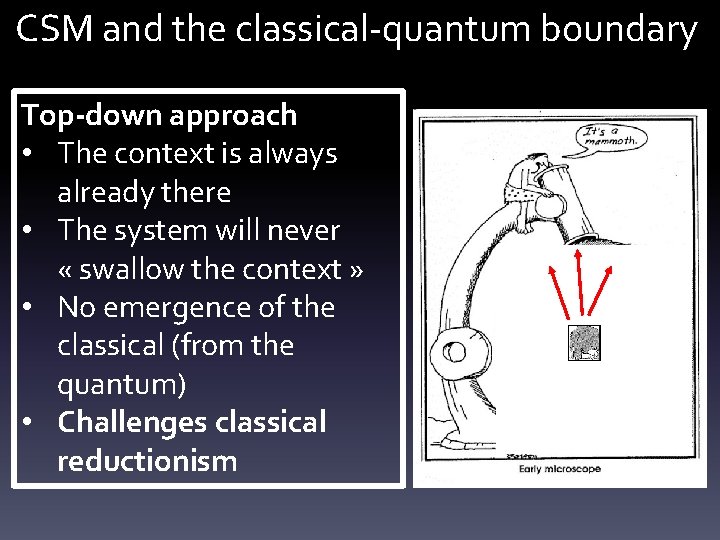
CSM and the classical-quantum boundary Top-down approach • The context is always already there • The system will never « swallow the context » • No emergence of the classical (from the quantum) • Challenges classical reductionism

The 2 alea • Epistemic randomness • Information loss due to coarsegraining • Bottom up approach • From microscopic to macroscopic • Ontological randomness • Unpredictability due to contextuality + quantization • Top down approach • From macroscopic to microscopic

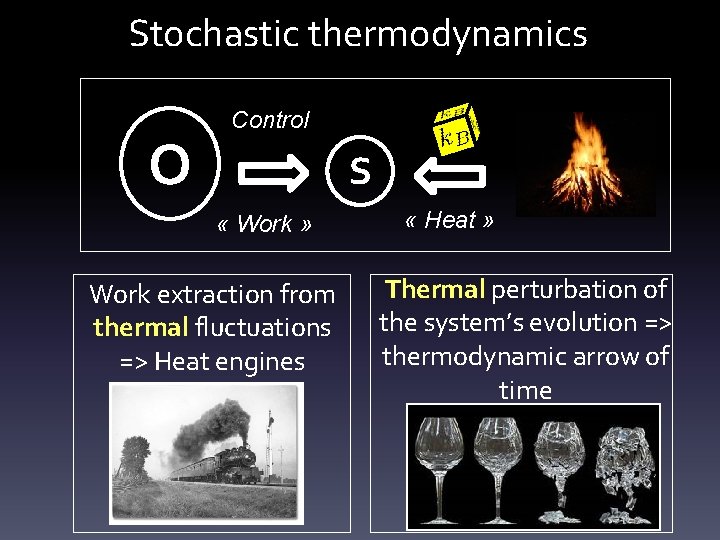
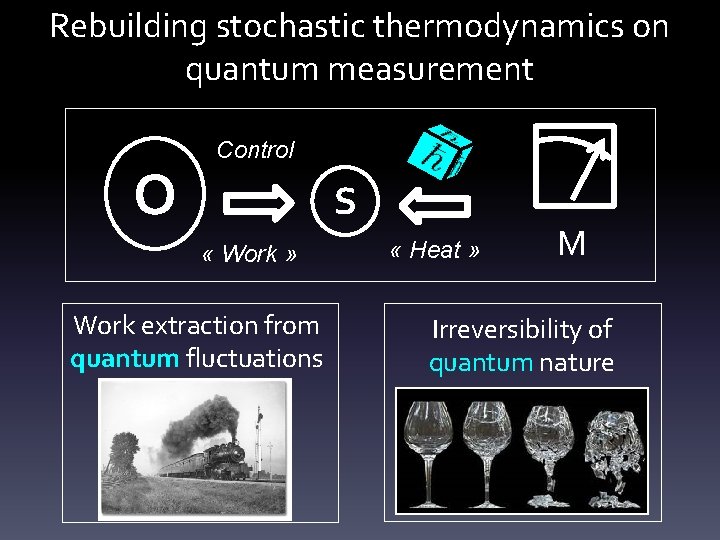
Stochastic thermodynamics O Control S « Work » « Heat » Stochastic thermodynamics = science of control against noise • Noise as a resource: engines • Noise as a lack of control: time arrow Pioneering approaches: Noise source was thermal

Stochastic thermodynamics O Control S « Work » Work extraction from thermal fluctuations => Heat engines « Heat » Thermal perturbation of the system’s evolution => thermodynamic arrow of time

Quantum stochastic thermodynamics? Hilbert space O Control S « Work » « Heat » • Quantum supremacy on heat engines performances? Impact of quantum coherence? • Irreversibility and fluctuation theorems in the quantum regime?

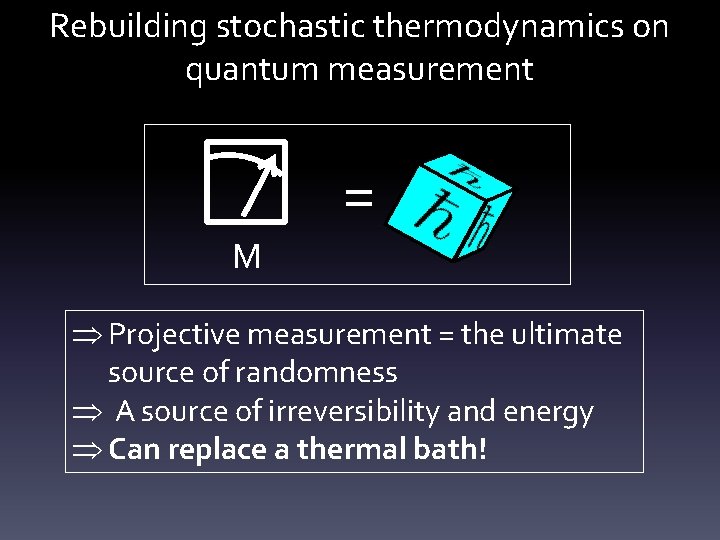
Rebuilding stochastic thermodynamics on quantum measurement = M Projective measurement = the ultimate source of randomness A source of irreversibility and energy Can replace a thermal bath!

Rebuilding stochastic thermodynamics on quantum measurement O Control S « Work » Work extraction from quantum fluctuations « Heat » M Irreversibility of quantum nature

Rebuilding stochastic thermodynamics on quantum measurement Featured in phys. org, Nature Research Highlights

Conclusions CSM approach: Quantum randomness is due to contextuality and quantization Unlike classical randomness (epistemic) quantum randomness is ontological The classical world does not emerge from the quantum: The quantum formalism essentially relies on a classical context

Outlooks Get CSM out of the lab! Context -> Environment Rethink epistemology vs ontology, given contextual objectivity Control O S M 1 C 1 S C 2 M 2 « Fertility » of the approach: rebuild quantum thermodynamics on M quantum randomness

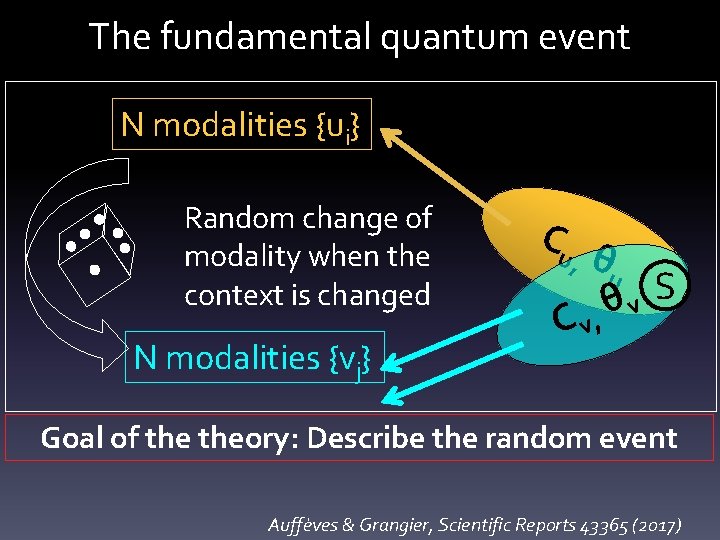
The fundamental quantum event N modalities {ui} Random change of modality when the context is changed N modalities {vj} Cu θu S θ v C v, , Goal of theory: Describe the random event Auffèves & Grangier, Scientific Reports 43365 (2017)

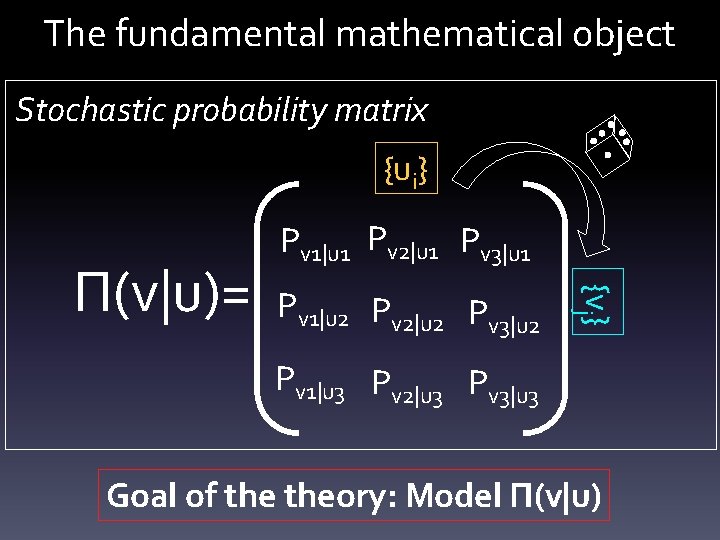
The fundamental mathematical object Stochastic probability matrix {ui} Pv 1|u 2 Pv 2|u 2 Pv 3|u 2 {vj} Π(v|u)= Pv 1|u 1 Pv 2|u 1 Pv 3|u 1 Pv 1|u 3 Pv 2|u 3 Pv 3|u 3 Goal of theory: Model Π(v|u)

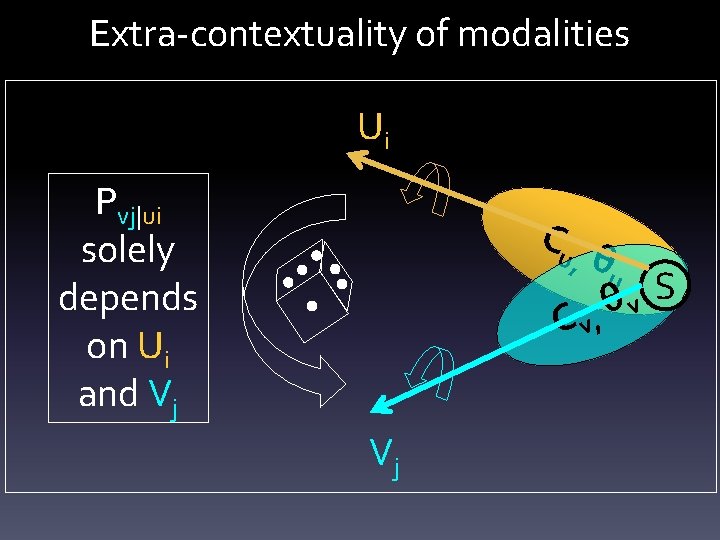
Extra-contextuality of modalities Ui Pvj|ui solely depends on Ui and Vj Cu θu S θ v C v, , Vj

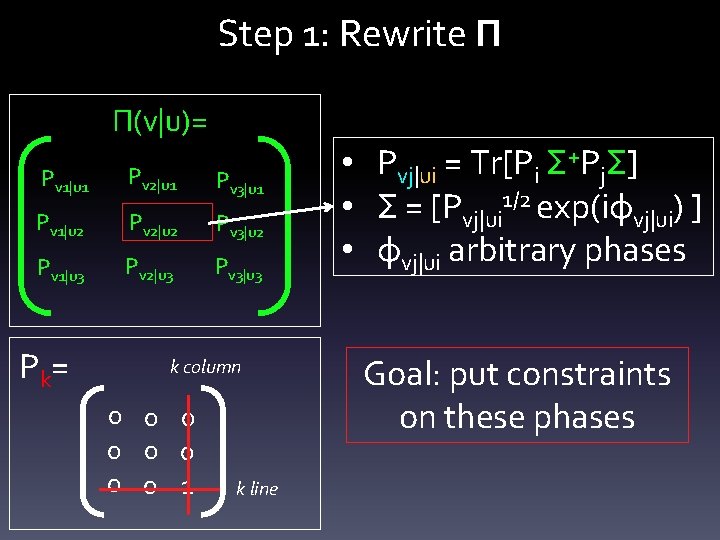
Step 1: Rewrite Π Π(v|u)= Pv 1|u 1 Pv 2|u 1 Pv 3|u 1 Pv 1|u 2 Pv 2|u 2 Pv 3|u 2 Pv 1|u 3 Pv 2|u 3 Pv 3|u 3 Pk= k column 0 0 0 0 1 k line • Pvj|ui = Tr[Pi Σ+PjΣ] • Σ = [Pvj|ui 1/2 exp(iφvj|ui) ] • φvj|ui arbitrary phases Goal: put constraints on these phases

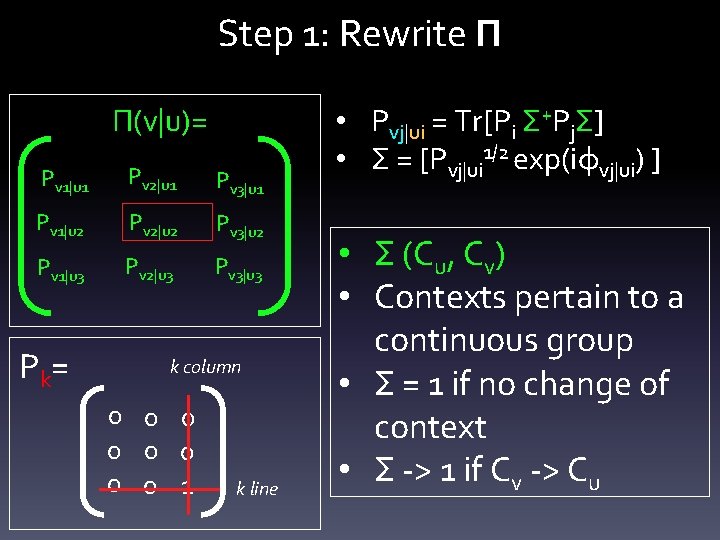
Step 1: Rewrite Π Π(v|u)= Pv 1|u 1 Pv 2|u 1 Pv 3|u 1 Pv 1|u 2 Pv 2|u 2 Pv 3|u 2 Pv 1|u 3 Pv 2|u 3 Pv 3|u 3 Pk= k column 0 0 0 0 1 k line • Pvj|ui = Tr[Pi Σ+PjΣ] • Σ = [Pvj|ui 1/2 exp(iφvj|ui) ] • Σ (Cu, Cv) • Contexts pertain to a continuous group • Σ = 1 if no change of context • Σ -> 1 if Cv -> Cu

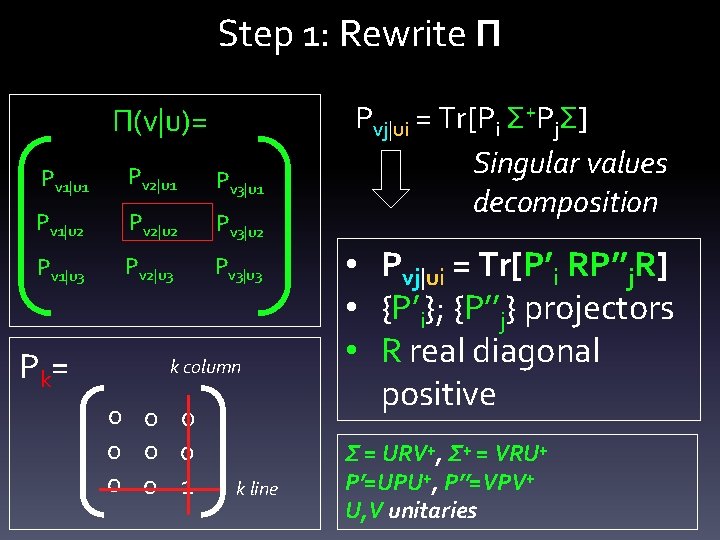
Step 1: Rewrite Π Π(v|u)= Pv 1|u 1 Pv 2|u 1 Pv 3|u 1 Pv 1|u 2 Pv 2|u 2 Pv 3|u 2 Pv 1|u 3 Pv 2|u 3 Pv 3|u 3 Pk= k column 0 0 0 0 1 k line Pvj|ui = Tr[Pi Σ+PjΣ] Singular values decomposition • Pvj|ui = Tr[P’i RP’’j. R] • {P’i}; {P’’j} projectors • R real diagonal positive Σ = URV+, Σ+ = VRU+ P’=UPU+, P’’=VPV+ U, V unitaries
![Step 2 Call ontology for help Pvjui TrPi RPj R Depends on Cu Step 2: Call ontology for help Pvj|ui = Tr[P’i RP’’j. R] Depends on Cu](https://slidetodoc.com/presentation_image_h/110b3abfa44ef8bd902a8c177d889c4b/image-70.jpg)
Step 2: Call ontology for help Pvj|ui = Tr[P’i RP’’j. R] Depends on Cu and Cv Identity for stochastic matrices Pvj|ui = Tr[P’i RP’’j. R] • R, P’i , P’’j depend on Ui Extraand Vj only contextuality • R, P’i , P’’j invariant when of modalities Cu -> Cu’ and Cv -> Cv’ keeping Ui and Vj unchanged
![Step 3 Chase the contradiction Wanted RUi Vj TrR 2 PkN Step 3: Chase the contradiction Wanted: R(Ui, Vj) • • • Tr[R 2 P’k]=N](https://slidetodoc.com/presentation_image_h/110b3abfa44ef8bd902a8c177d889c4b/image-71.jpg)
Step 3: Chase the contradiction Wanted: R(Ui, Vj) • • • Tr[R 2 P’k]=N Tr[R 2]=N For each k Tr[(R 2 -1)P’k]=0 N linear equations D=Det [|Um, n|2] Either R=1, or D=0 • Suppose R(Cu , Cv) ≠ 1 => D(Cu , Cv)=0 • Cu -> C’u ; Cv -> C’v => D≠ 0 => R(C’u , C’v)=1 • R depends on the whole contexts ABSURD => R=1
![Step 4 Unitary matrices Pvjui TrPi ΣPjΣ Σ Pvjui 12 expiφvjui Step 4: Unitary matrices Pvj|ui = Tr[Pi Σ+PjΣ] Σ = [Pvj|ui 1/2 exp(iφvj|ui) ]](https://slidetodoc.com/presentation_image_h/110b3abfa44ef8bd902a8c177d889c4b/image-72.jpg)
Step 4: Unitary matrices Pvj|ui = Tr[Pi Σ+PjΣ] Σ = [Pvj|ui 1/2 exp(iφvj|ui) ] Σ = URV+, Σ+ = VRU+ U, V unitaries R=1 => Σ = Σ+= Σ-1 Real matrices? Continuity of contexts Continuous path relating identity and permutation Σ = complex, unitary matrix
![And finally Usual quantum formalism Pvjui TrPi ΣvuPjΣvu Pvjui TrΣvu And finally: Usual quantum formalism • Pvj|ui = Tr[Pi Σv|u+PjΣv|u] • Pvj|ui = Tr[Σv|u.](https://slidetodoc.com/presentation_image_h/110b3abfa44ef8bd902a8c177d889c4b/image-73.jpg)
And finally: Usual quantum formalism • Pvj|ui = Tr[Pi Σv|u+PjΣv|u] • Pvj|ui = Tr[Σv|u. Pi Σv|u+Pj] V j • • • Ui, Vj = Rays in a Hilbert space Change of context = Σv|u unitary Probabilities follow Born’s rule Ui