What is Q Interpretation 1 intercept Interpretation 2





- Slides: 13

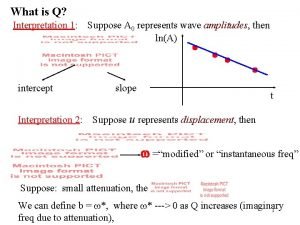
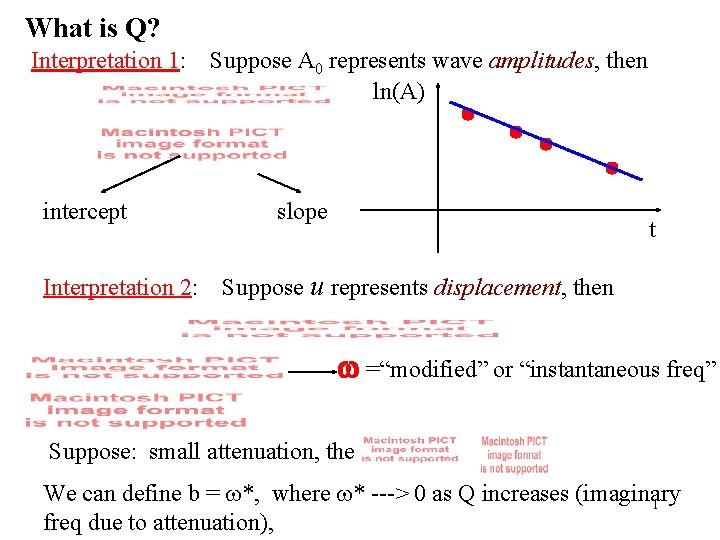
What is Q? Interpretation 1: intercept Interpretation 2: Suppose A 0 represents wave amplitudes, then ln(A) slope t Suppose u represents displacement, then w =“modified” or “instantaneous freq” Suppose: small attenuation, the We can define b = w*, where w* ---> 0 as Q increases (imaginary 1 freq due to attenuation),

Relation with velocity: Imaginary velocity due to attenuation So Q is a quantity that defines the relationship between real and imaginary frequency (or velocity) under the influence of attenuation. Interpretation 3: Q is the number of cycles the oscillations take to decay to a certain amplitude level. So amplitude at time tn (after n cycles) 2

Attenuation and Physical Dispersion (continued…) Different interpretations of Q (quality factor): (1) As a damping term Q = w 0/g (2) As a fraction between imaginary and real frequencies (or imaginary velocity to real velocity) (3) As the number of cycles for a wave to decay to a certain amplitude. If n = Q, then (4) Connection with t* (for body wave). 1 number that describes Q structure of several layers (5) Energy formula 3

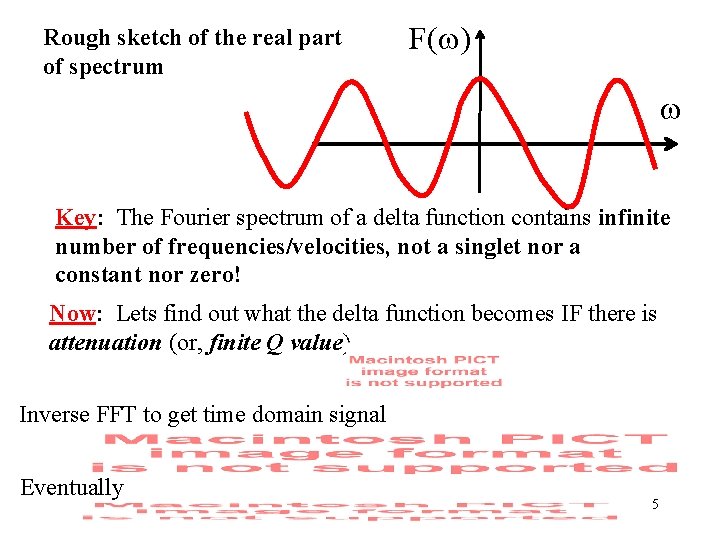
Effects of Q (assume the SAME Q value) dependencies (2) Physical dispersion: different frequency component travels at different times, hence causing broadening of phase pulse. Lets assume a Dirac delta function: area = 1, infinite height. u(x, t) spectrum t

Rough sketch of the real part of spectrum F(w) w Key: The Fourier spectrum of a delta function contains infinite number of frequencies/velocities, not a singlet nor a constant nor zero! Now: Lets find out what the delta function becomes IF there is attenuation (or, finite Q value). Inverse FFT to get time domain signal Eventually 5

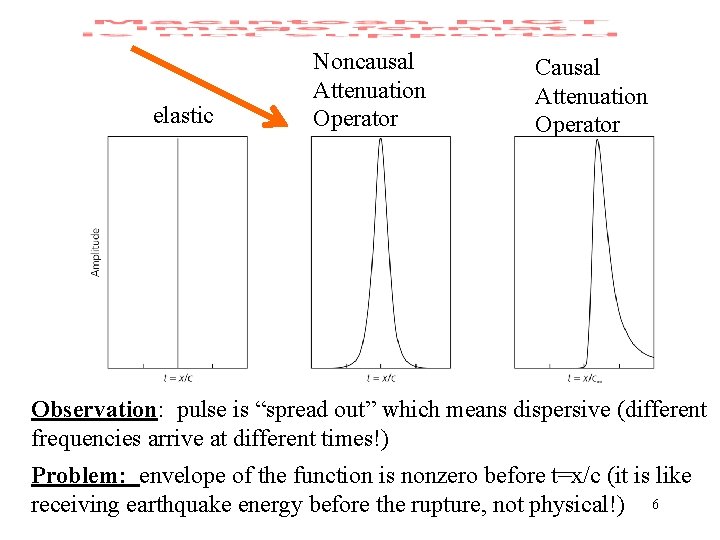
elastic Noncausal Attenuation Operator Causal Attenuation Operator Observation: pulse is “spread out” which means dispersive (different frequencies arrive at different times!) Problem: envelope of the function is nonzero before t=x/c (it is like receiving earthquake energy before the rupture, not physical!) 6

How to make this process causal? One of the often-cited solutions: Azimi’s Attenuation Law: Where does it come from? Answer: Derived under the following causality condition: Physical Models of Anelasticity In an nutshell, Earth is composed of lots of Viscoelastic (or Standard Linear) Solids 7

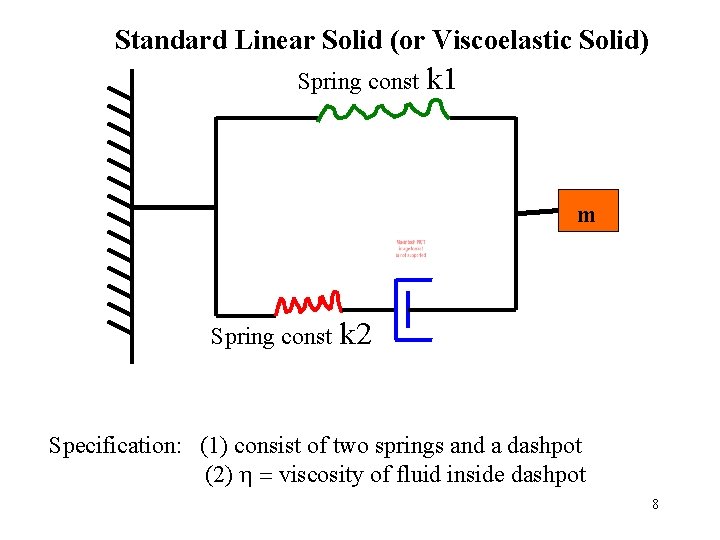
Standard Linear Solid (or Viscoelastic Solid) Spring const k 1 m Spring const k 2 Specification: (1) consist of two springs and a dashpot (2) h = viscosity of fluid inside dashpot 8

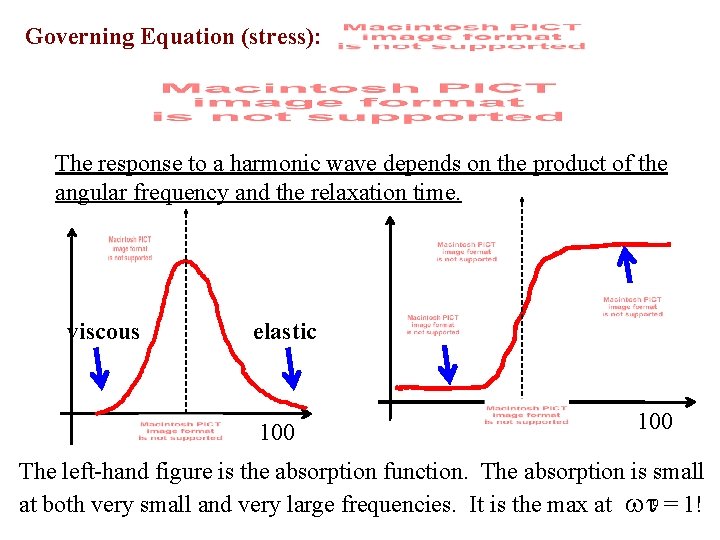
Governing Equation (stress): The response to a harmonic wave depends on the product of the angular frequency and the relaxation time. viscous elastic 100 The left-hand figure is the absorption function. The absorption is small at both very small and very large frequencies. It is the max at wt 9 = 1!

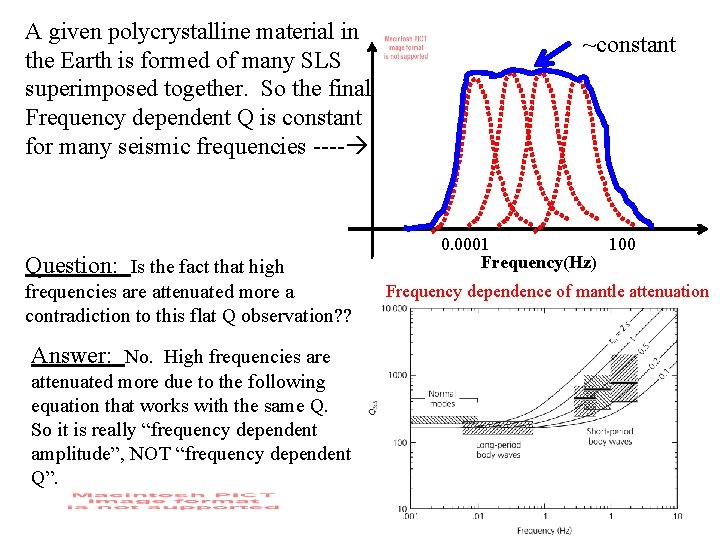
A given polycrystalline material in the Earth is formed of many SLS superimposed together. So the final Frequency dependent Q is constant for many seismic frequencies ---- Question: Is the fact that high frequencies are attenuated more a contradiction to this flat Q observation? ? ~constant 100 0. 0001 Frequency(Hz) Frequency dependence of mantle attenuation Answer: No. High frequencies are attenuated more due to the following equation that works with the same Q. So it is really “frequency dependent amplitude”, NOT “frequency dependent Q”. 10

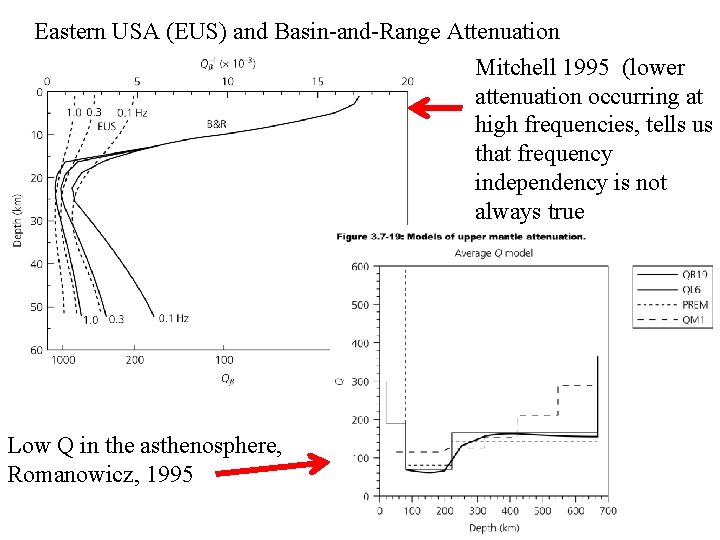
Eastern USA (EUS) and Basin-and-Range Attenuation Mitchell 1995 (lower attenuation occurring at high frequencies, tells us that frequency independency is not always true Low Q in the asthenosphere, Romanowicz, 1995 11

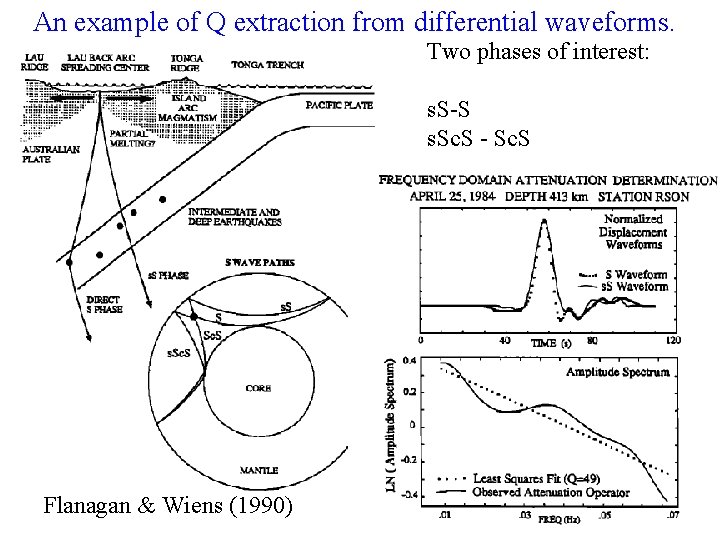
An example of Q extraction from differential waveforms. Two phases of interest: s. S-S s. Sc. S - Sc. S Flanagan & Wiens (1990) 12

Key Realization: The two waveforms are similar in nature, mainly differing by the segment in the above source (the small depth phase segment) Approach: Spectral division of S from SS, then divide out the 13 accounts for the Crustal operator (a function in freq that of the additional propagation in a normal crust) Spectral dividing S and R will leave the attenuation term A(w) (slope = =t/2 Q, t = time diff of s. S-S)
 X intercept form
X intercept form X intercept and y intercept
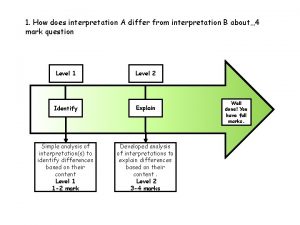
X intercept and y intercept How does interpretation b differ from interpretation a
How does interpretation b differ from interpretation a How to write an equation in slope intercept form
How to write an equation in slope intercept form Survey method of data collection
Survey method of data collection How to change standard form to slope intercept form
How to change standard form to slope intercept form X and y math
X and y math Slope intercept form jeopardy
Slope intercept form jeopardy Unit 2 linear equations
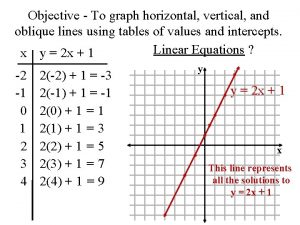
Unit 2 linear equations Horizontal vertical oblique
Horizontal vertical oblique Point-slope form definition geometry
Point-slope form definition geometry Sequential intercept model template
Sequential intercept model template Y=ax^2 parabola
Y=ax^2 parabola The music store
The music store