What is Physics The study of matter energy

What is Physics? • The study of matter, energy, and the interaction between them • Physics is about asking fundamental questions and trying to answer them by observing, hypothesizing, experimenting, and communicating • Physics involves the study of the physical world from the largest of scales (e. g. the universe as a whole) to the smallest of scales (e. g. subatomic particles) • Can you be more specific? . See http: //www. physics. org/article-questions. asp? id=18

What do Physicists Study?

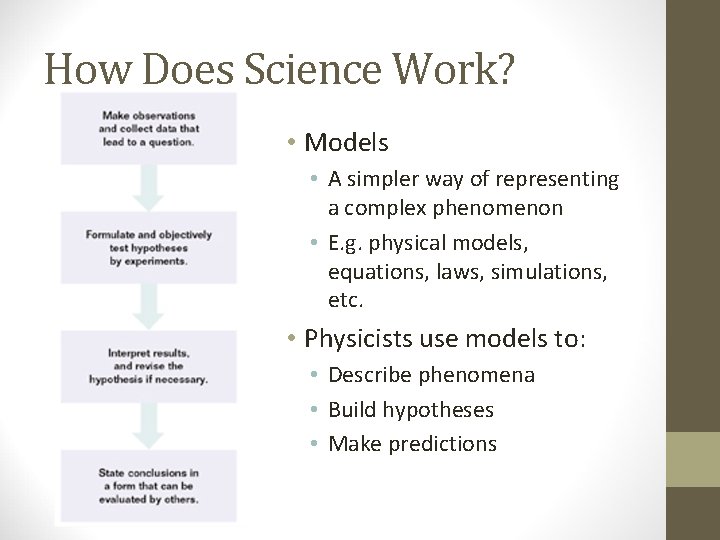
How Does Science Work? • Models • A simpler way of representing a complex phenomenon • E. g. physical models, equations, laws, simulations, etc. • Physicists use models to: • Describe phenomena • Build hypotheses • Make predictions

Two Types of Science • Basic science involves questions and research about the fundamental nature of the physical world • Applied science involves questions with a view toward solving a problem

1. 2 Measurement in Experiments

Learning Objectives • • List basic SI units and quantities they describe Convert measurements to scientific notation Distinguish between accuracy & precision Use significant figures in measurements & calculations

Numbers as Measurements • In science, numbers represent measurements • Numbers involve three things • Magnitude how much? • Dimensions length, mass, time • Units of what?

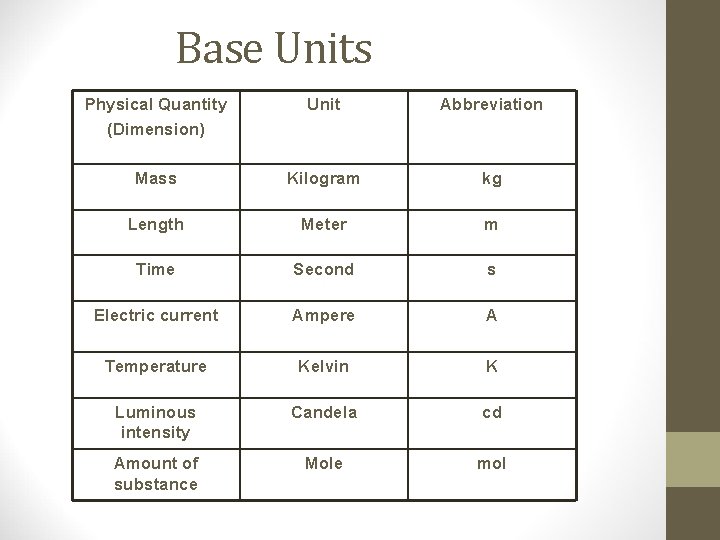
The SI system • The standard measurement system for science • Formerly called the metric system • Base units • Basic units that are not a combination of some other units • Derived units • Are combinations of base units

Base Units Physical Quantity (Dimension) Unit Abbreviation Mass Kilogram kg Length Meter m Time Second s Electric current Ampere A Temperature Kelvin K Luminous intensity Candela cd Amount of substance Mole mol

Derived units • Derived units are combinations of base units Base Unit Derived Unit m (length) m 3 (volume) kg (mass) m (length) s (time) N (newton) force 1 N = 1 kg∙m s 2

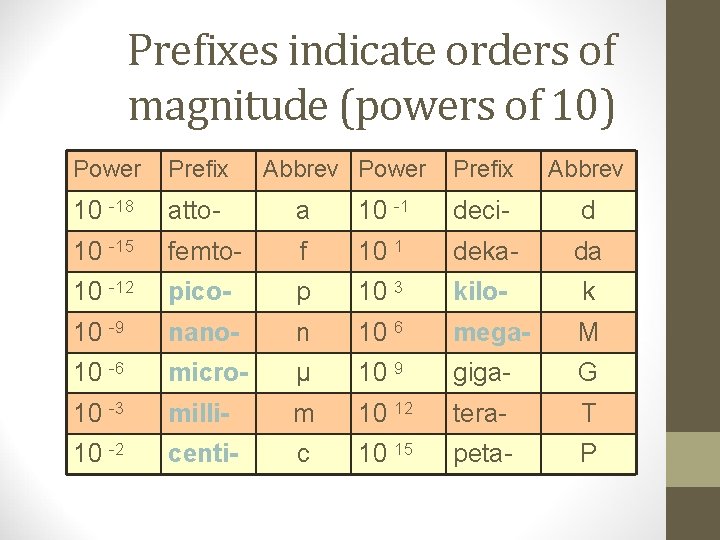
Prefixes indicate orders of magnitude (powers of 10) Power Prefix Abbrev 10 -18 atto- a 10 -1 deci- d 10 -15 femto- f 10 1 deka- da 10 -12 pico- p 10 3 kilo- k 10 -9 nano- n 10 6 mega- M 10 -6 micro- μ 10 9 giga- G 10 -3 milli- m 10 12 tera- T 10 -2 centi- c 10 15 peta- P

Converting Prefixes & Units • The main idea: multiply the given unit by a conversion factor yielding the desired unit • Conversion factor: a ratio of two units that is an equivalent to 1. • Example: convert millimeters to meters 1 mm x 10 -3 m = 1 x 10 -3 m 1 mm Practice 1 A, #1 -5

Converting units of area and units of volume • How many cm 2 are in 1 m 2? • How many cm 3 are in 1 m 3? • How many in 3 are in 1 L? • 1 in = 2. 54 cm • 1 L = 103 m. L • 1 m. L = 1 cm 3

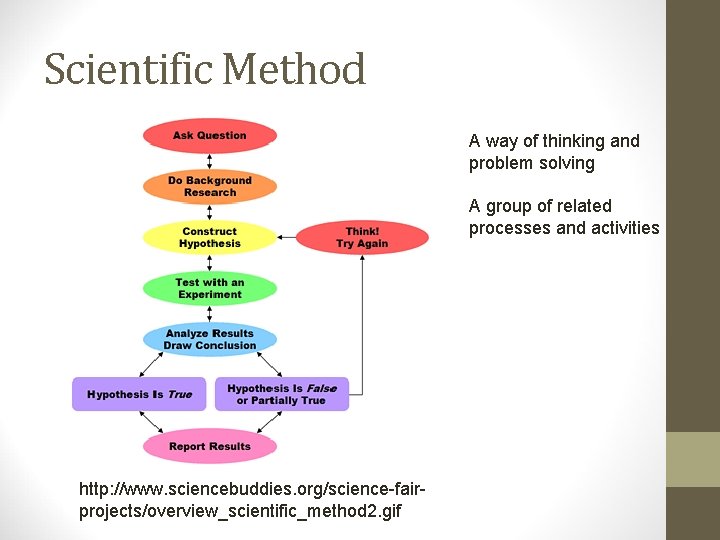
Scientific Method A way of thinking and problem solving A group of related processes and activities http: //www. sciencebuddies. org/science-fairprojects/overview_scientific_method 2. gif

Scientific Method: Important Terms • Law vs. Theory • Describes vs. explains • Fact & Observation • a scientific fact is an objective and verifiable observation • Hypothesis • Tentative explanation • testable • Experiment • Test of the hypothesis

Accuracy & Precision • Accuracy • Nearness of a measurement to the true value • Precision • Degree of exactness or refinement of a measurement • Repeatability of a measurement

Precision • describes the limit of exactness of a measuring instrument • Significant figures reflect certainty of a measurement • Are figures that are known because they are measured

Significant Figures • Represent measured numbers (numbers known with certainty) and one final estimated digit • Reflect the precision of an instrument • Must be reported properly • Require special handling in calculations

Rules to determine significant digits 1. All non-zeros ARE 2. All zeros between non-zeros ARE 3. Zeros in front of non-zeros ARE NOT 4. Final zeros to right of decimal ARE 5. Final zeros without a decimal ARE NOT 6. Final zeros to left of decimal ARE

How many significant figures? • 50. 3 • 3. 0025 • 0. 892 • 0. 0008 • 57. 00 • 2. 000000 • 1000 • 20. 001 3426 210 6. 58 x 103 1. 534 x 10 -4 2. 00 x 107 5000. 30

Rules of calculating with significant figures 1. 2. 3. When adding & subtracting, final answer must have fewest decimal places present in the calculation. When multiplying & dividing, final answer must have fewest significant digits present in the calculation. Number of figures in a constant or exact numbers are do not affect calculations involving sig figs.

Uncertainty in Measurement • • No measurement is correct with 100% precision. All measurements are approximations Therefore, all measurements have a degree of uncertainty This means that measurements should be described with their degree of uncertainty

Uncertainty in measurement defines the range in which the true value is found. • Estimated uncertainty • ± one half smallest increment of measurement • E. g. a ruler graduated in 0. 1 cm units would be reported as 5. 2 ± 0. 05 cm • So the true value of the measurement lies between 5. 2 - 0. 05 and 5. 2 - 0. 05 cm • The actual value is between 5. 15 cm and 5. 25 cm

Is this diamond yours? • Use estimated uncertainty to answer this question • You have a diamond with a mass of 8. 17 grams, measured on a scale with a precision of 0. 01 g • You lend the diamond to a friend, who returns it. The returned diamond measures 8. 16 g • Assuming the balance is operating properly, is the diamond yours? • Why or why not?

Fractional and percent uncertainty • Fractional uncertainty • Helps describe the degree of uncertainty relative to the amount being measured • Is the estimated uncertainty divided by the measurement • In this example it is 0. 05/5. 2 =. 0096 cm • What happens to fractional uncertainty as the magnitude of the measure increases? • Percent uncertainty • = fractional uncertainty x 100 • 0. 0096 = 0. 96% • Measurement is reported as 5. 2 ± 0. 96%

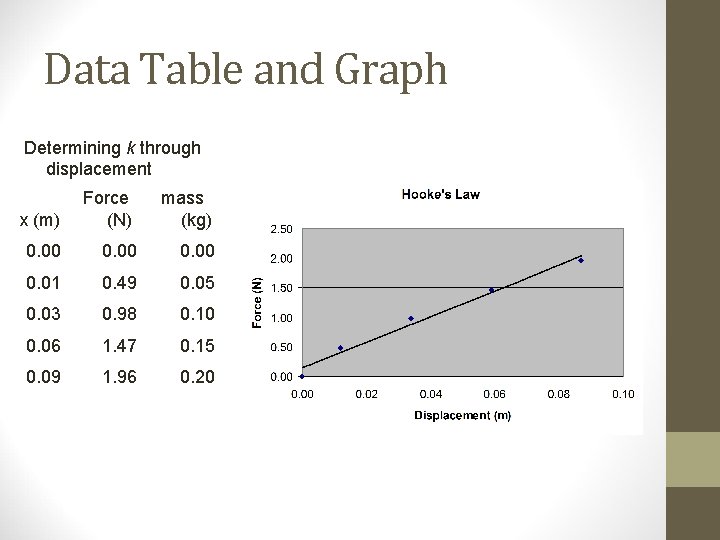
1. 3 Language of Physics • Mathematics is the language of physics • Data is collected in a table form • Data is graphed to show relationship of independent & dependent variables

Data Table and Graph Determining k through displacement x (m) Force (N) mass (kg) 0. 00 0. 01 0. 49 0. 05 0. 03 0. 98 0. 10 0. 06 1. 47 0. 15 0. 09 1. 96 0. 20

Equations indicate relationships of variables

Evaluating Physics Equations • Dimensional analysis can give you clues how to solve a problem • Dimensional analysis can help check many types of problems because… • Dimensions can be treated as algebraic quantities • Example: derive a formula for speed • Example: How long would it take a car to travel 725 km at a speed of 88 km/h?

Order of Magnitude Estimates • Physics often uses very large and very small numbers • Using powers of ten as estimates of the numbers can help estimate and check your answers • Example: from the previous problem,

Order of Magnitude Estimates • What would be a reasonable order of magnitude estimate for…. • The length of a soccer field in meters? • The mass of a sparrow in kg? • The length of a fly meters? • How much time would it take for a fly to fly from one end of the school building to the other?