What is oscillatory motion Oscillatory motion occurs when



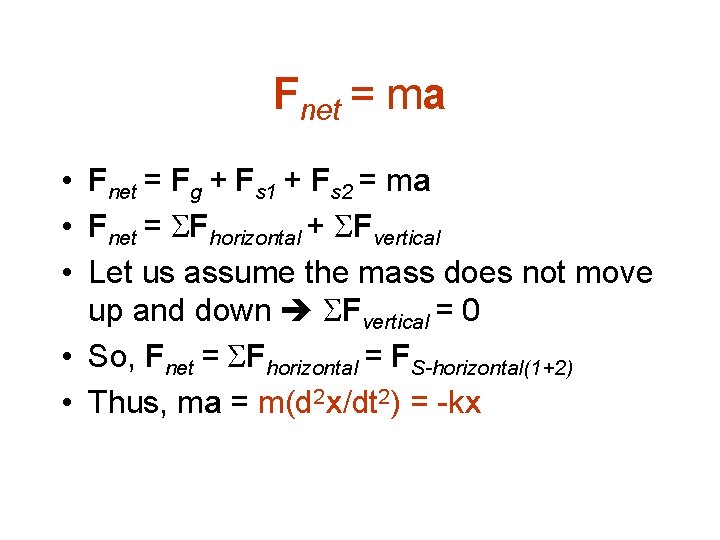











- Slides: 20

What is oscillatory motion? • Oscillatory motion occurs when a force acting on a body is proportional to the displacement of the body from equilibrium. F x • The Force acts towards the equilibrium position causing a periodic back and forth motion.

What are some examples? • • Pendulum Spring-mass system Vibrations on a stringed instrument Molecules in a solid Electromagnetic waves AC current Many other examples…

What do these examples have in common? • Time-period, T. This is the time it takes for one oscillation. • Amplitude, A. This is the maximum displacement from equilibrium. • Period and Amplitude are scalers.

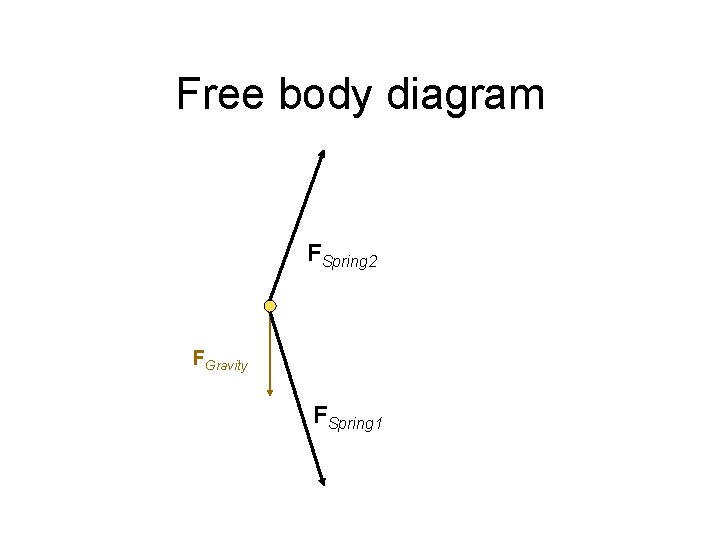
Forces • Consider a mass with two springs attached at opposite ends… • We want to find an equation for the motion. • How should we start? • Free-body diagram!!

Free body diagram FSpring 2 FGravity FSpring 1
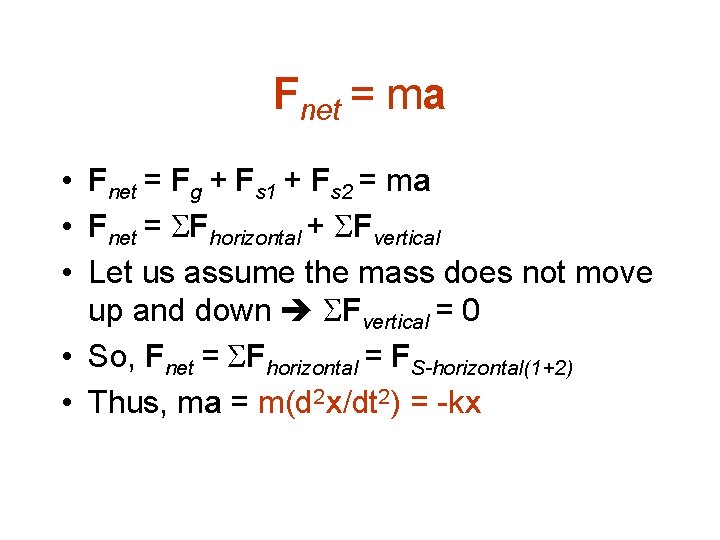
Fnet = ma • Fnet = Fg + Fs 1 + Fs 2 = ma • Fnet = Fhorizontal + Fvertical • Let us assume the mass does not move up and down Fvertical = 0 • So, Fnet = Fhorizontal = FS-horizontal(1+2) • Thus, ma = m(d 2 x/dt 2) = -kx

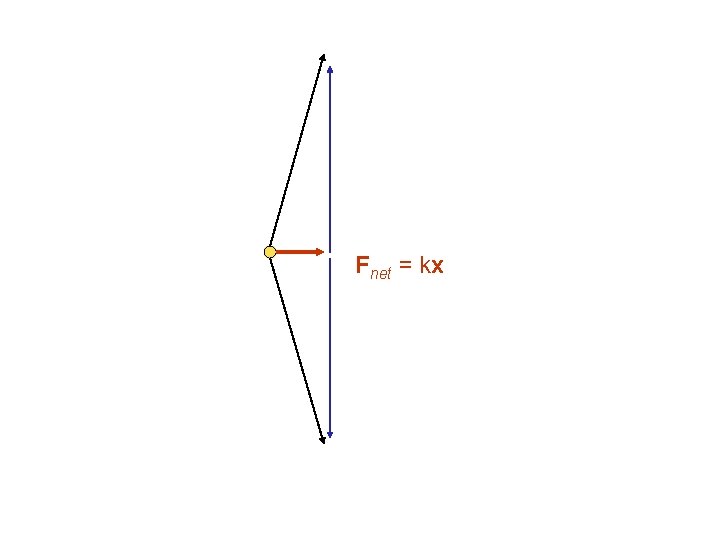
Fnet = kx

ma = m(d 2 x/dt 2) = -kx • Let k/m = (d 2 x/dt 2) + x = 0 • This is the second order differential equation for a harmonic oscillator. It is your friend. It has a unique solution…

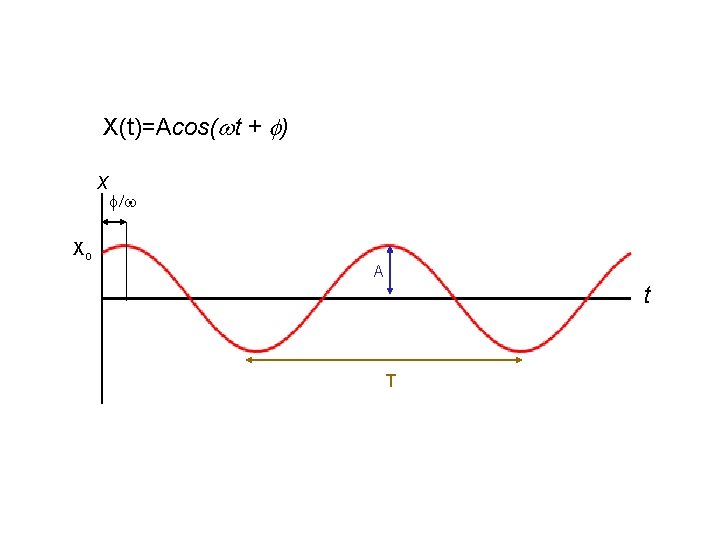
Simple Harmonic motion • The displacement for a simple harmonic oscillator in one dimension is… x(t) = Acos( t + § is the angular frequency. It is constant. § is the phase constant. It depends on the initial conditions. • What is the velocity? • What is the acceleration?

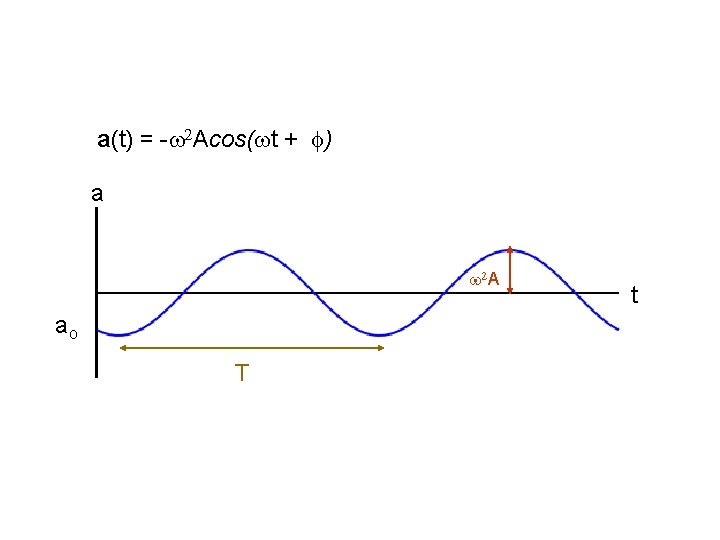
• Velocity: differentiate x with respect to t. dx/dt = v(t) = - Asin( t + ) • Acceleration: differentiate v with respect to t. dv/dt = a(t) = - Acos( t + )

X(t)=Acos( t + ) x Xo A t T

a(t) = - Acos( t + ) a A ao T t t

Using data • The accelerometer will give us all the information we need to confirm our analysis • We can measure all the parameters of this particular system and use them to predict the results of the accelerometer.

What can we measure without the accelerometer? • • • The mass, m Hooke’s constant, k That’s all! T = 2 / = 2 m/k)1/2 (Recall = k/m) Everything else depends on the initial conditions. What does this tell us? • The time period, T, is independent of the initial conditions!

Energy • The system operates at a particular frequency, v, regardless of the energy of the system. v = 1/T = 2 (k/m)1/2 • The energy of the system is proportional to the square of the amplitude. E = (1/2)k. A 2

Proof of E=(1/2)k. A 2 • Kinetic Energy = (1/2)mv 2 V = SIN( t + ) (1/2)M A SIN 2 ( t + ) • Elastic potential energy U=(1/2)kx 2 x = Acos( t + ) U (1/2)k. A 2 cos 2. /( t + )

E=K+U= (1/2)k. A 2[sin 2 ( t + ) + cos 2 ( t + )] = (1/2)k. A 2

Damping • Simple harmonic motion is really a simplified case of oscillatory motion where there is no friction (remember our FBD) • For small to medium data sets this will not affect our results noticeably.

for the rest of class. . . • We are going to find k and m and compare to the results of the accelerometer

Some cool oscillatory motion websites • • http: //www. phy. ntnu. edu. tw/ntnujava/viewtopic. php? t=236 http: //www. kettering. edu/~drussell/Demos/SHO/mass. html http: //farside. ph. utexas. edu/teaching/301/lectures/node 136. html http: //www. physics. uoguelph. ca/tutorials/shm/Q. shm. html