WHAT IS GEOMETRY GEOMETRY FROM THE ANCIENT GREEK

WHAT IS GEOMETRY ? GEOMETRY (FROM THE ANCIENT GREEK: ΓΕΩΜΕΤΡΊΑ; GEO- "EARTH", -METRON "MEASUREMENT") IS A BRANCH OF MATHEMATICS CONCERNED WITH QUESTIONS OF SHAPE, SIZE, RELATIVE POSITION OF FIGURES, AND THE PROPERTIES OF SPACE. A MATHEMATICIAN WHO WORKS IN THE FIELD OF GEOMETRY IS CALLED A GEOMETER.

KEY WORDS • PARALLEL • PERPENDICULAR BISECTOR • ANGLE BISECTOR • PARALLELOGRAM • BASE • HEIGHT

PLANES A PLANE CAN BE THOUGHT OF AS A TWO-DIMENSIONAL FLAT SURFACE, HAVING LENGTH AND WIDTH, BUT NO HEIGHT. A PLANE EXTENDS INDEFINITELY ON ALL SIDES AND IS COMPOSED OF AN INFINITE NUMBER OF POINTS AND LINES. ONE WAY TO THINK ABOUT A PLANE IS AS A SHEET OF PAPER WITH INFINITE LENGTH AND WIDTH.

BASIC GEOMETRY TERMS POINTS IN GEOMETRY, WE USE POINTS TO SPECIFY EXACT LOCATIONS. THEY ARE GENERALLY DENOTED BY A NUMBER OR LETTER. BECAUSE POINTS SPECIFY A SINGLE, EXACT LOCATION, THEY ARE ZERO-DIMENSIONAL. IN OTHER WORDS, POINTS HAVE NO LENGTH, WIDTH, OR HEIGHT. IT MAY BE HELPFUL TO THINK OF A POINT AS A MINISCULE "DOT" ON A PIECE OF PAPER. POINTS A, B, AND C

LINES IN GEOMETRY MAY BE THOUGHT OF AS A “STRAIGHT” LINE THAT CAN BE DRAWN ON PAPER WITH PENCIL AND RULER. A LINE IS ONE-DIMENSIONAL, HAVING LENGTH, BUT NO WIDTH OR HEIGHT. A LINE EXTENDS INDEFINITELY IN BOTH DIRECTION.

LINES SEGMENTS LINE SEGMENT IS A PART OF A LINE THAT IS BOUNDED BY TWO DISTINCT END POINTS, AND CONTAINS EVERY POINT ON THE LINE BETWEEN ITS ENDPOINTS.

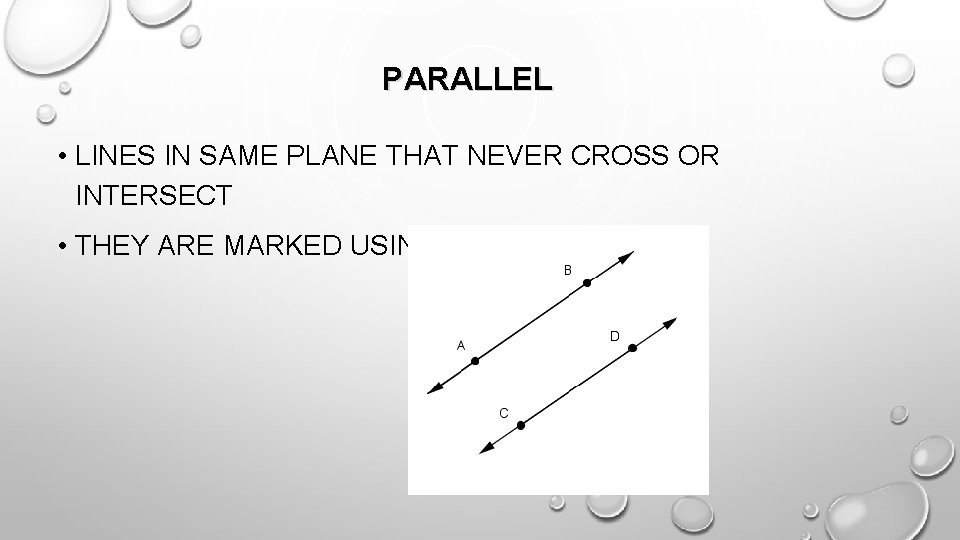
PARALLEL • LINES IN SAME PLANE THAT NEVER CROSS OR INTERSECT • THEY ARE MARKED USING “ARROWS”

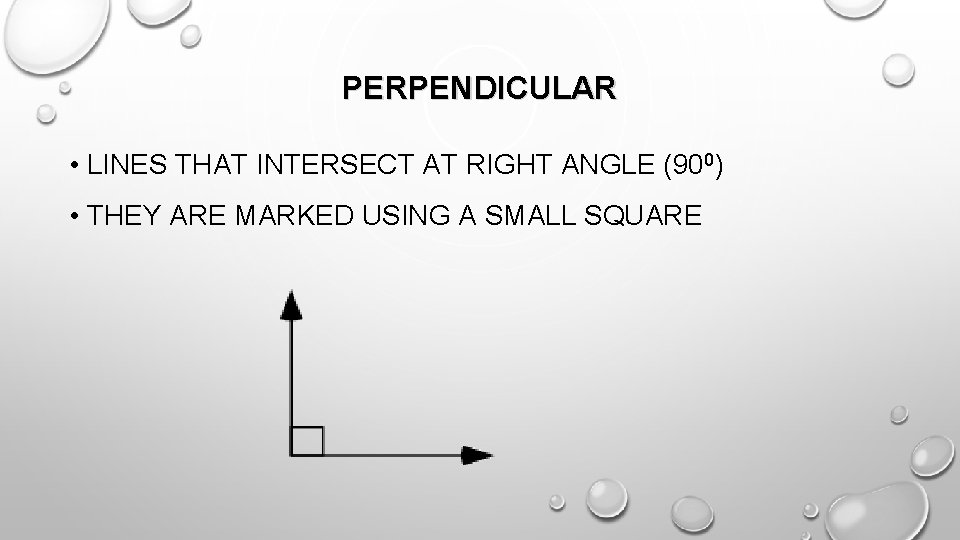
PERPENDICULAR • LINES THAT INTERSECT AT RIGHT ANGLE (900) • THEY ARE MARKED USING A SMALL SQUARE

PERPENDICULAR BISECT • BI MEANS “TWO” SECT MEANS “CUT”. SO, TO BISECT MEANS TO CUT IN TWO • PERPENDICULAR BISECT • A LINE THAT DIVIDES A LINE SEGMENT IN HALF AND IS AT RIGHT ANGLES TO IT. • EQUAL LINE SEGMENTS ARE MARKED WITH “HASH” MARKS

DRAW A PERPENDICULAR BISECTOR A BRIDGE OVER A RIVER NEEDS A PERPENDICULAR SUPPORT UNDER IT. DRAW THE SUPPORT IN THE MIDDLE OF THE BRIDGE. (CREATE USING COMPASS, USING A RULER AND RIGHT TRIANGLES, AND USING PAPER FOLDING. )

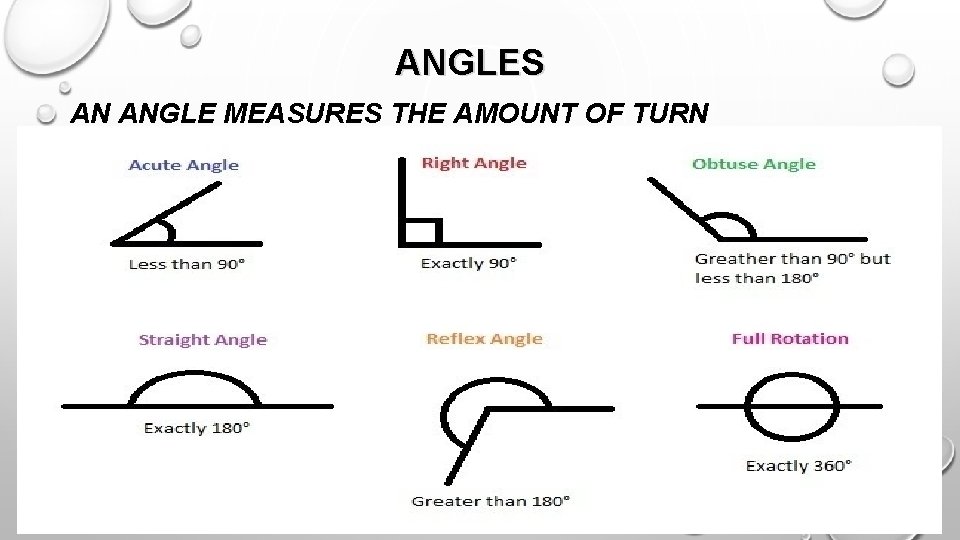
ANGLES AN ANGLE MEASURES THE AMOUNT OF TURN

PARALLELOGRAM

PARALLELOGRAM => A FOUR-SIDED FIGURE WITH OPPOSITE SIDES PARALLEL AND EQUAL IN LENGTH BASE => A SIDE OF A TWO-DIMENSIONAL CLOSED FIGURE. COMMON SYMBOL IS B HEIGHT => THE PERPENDICULAR DISTANCE FROM THE BASE TO THE OPPOSITE SIDE. COMMON SYMBOL IS H

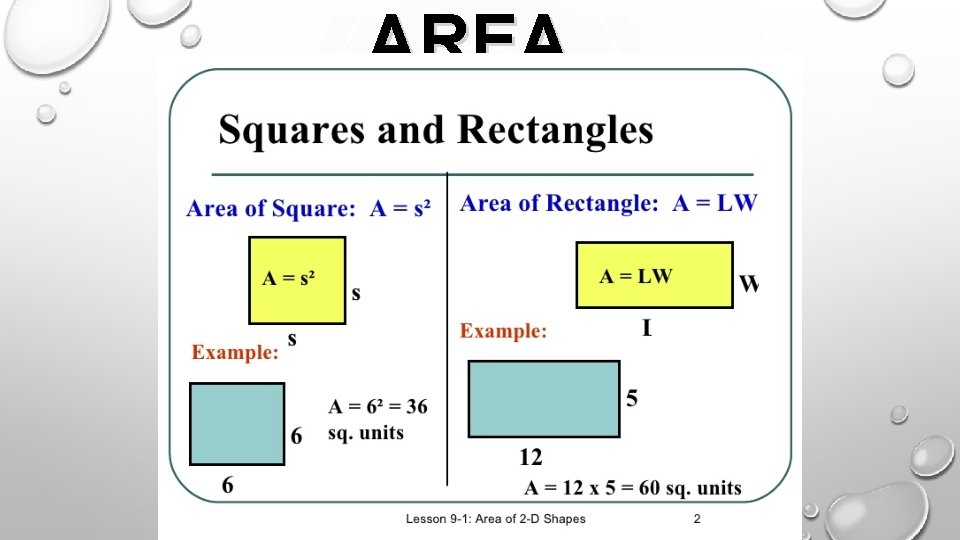
AREA

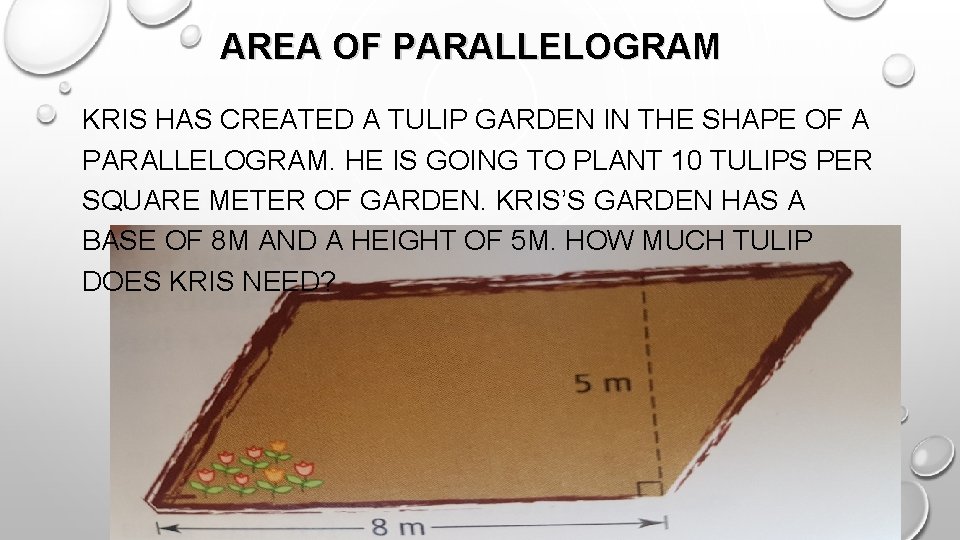
AREA OF PARALLELOGRAM KRIS HAS CREATED A TULIP GARDEN IN THE SHAPE OF A PARALLELOGRAM. HE IS GOING TO PLANT 10 TULIPS PER SQUARE METER OF GARDEN. KRIS’S GARDEN HAS A BASE OF 8 M AND A HEIGHT OF 5 M. HOW MUCH TULIP DOES KRIS NEED?

TRIANGLE