What is Computer Science About Part 1 Computational

What is Computer Science About? Part 1: Computational Thinking

Main Points • There is more to Computer Science than just programming. • Computer Science is about computational thinking and algorithms. • We try to formalize activities into repeatable procedures and concrete decisions. • Generalizing a procedure into an abstract algorithm helps us recognize if there are known solutions, and how complex the problem is. • Programming is just translating an algorithm into a specific syntax.

Some definitions. . . • Computational thinking – translating processes/procedures into step-by-step activities with well-defined choice points and decision criteria • Design and analysis of algorithms – expression of a procedure in terms of operations on abstract data structures like graphs, lists, strings, and trees – finite number of steps (clear termination conditions; it has to halt) – is the algorithm correct? – are all cases handled, or might it fail on certain inputs? – how much time will it take? how much space (memory)? • Programming – translating algorithms into a specific language • Software engineering – managing the development and life-cycle of a system, including design/specification, documentation, testing, use of components/libraries, release of new/updated versions – usually a team effort

Computational Thinking • CT has infused into all kinds of fields from cooking and sports, to transportation, medical diagnosis, and particle physics • Many intelligent activities are often ill-defined, and CT is about formalizing them into concrete decisions and repeatable procedures – Think about how to find a good place to eat in a new town • ask a friend? desired type of food? consult Zagat’s? look for restaurant with many cars in the parking lot? – Think about how choose a book to read • interest? availability? recommendations? reviews? – “Finding Waldo” (how do you search for shapes in images? )

Google’s ideas on Computational Thinking http: //www. google. com/edu/computational-thinking/what-is-ct. html Four components: Example: baking a cake Computationally: DECOMPOSITION breaking a problem into (decoupled) sub-problems mixing dry ingredients, then wet ingredients divide-and-conquer PATTERN RECOGNITION crack egg 1, identifying repeatable crack egg 2, operations crack egg 3. . . for/while-loops, sub-routines GENERALIZATION and ABSTRACTION baking chocolate cake or carrot cake or pound cake is similar, except add/substitute a few different ingredients adding parameters to code; also, can we apply the same procedure to other data like vectors, arrays, lists, trees, graphs? ALGORITHM DESIGN formalize procedure into recipe others can use; define things like how you know when it is done (bake 30 min at 350 or until crust is “golden”. . . ) step-by-step procedure with clear initialization, decision and termination conditions

• Mechanical analogies – Think about how a thermostat does temperature control

• Mechanical analogies – Think about how a thermostat does temperature control • What are the actions that can be taken? • What are the conditions under which these actions are triggered? • What parameters affect these decisions?

• Mechanical analogies – Think about how a thermostat does temperature control • What are the actions that can be taken? • What are the conditions under which these actions are triggered? • What parameters affect these decisions? Let T be the desired or “control” temperature if temp>T, turn on Air. Conditioner if temp<T, turn on Heater

• Mechanical analogies – Think about how a thermostat does temperature control • What are the actions that can be taken? • What are the conditions under which these actions are triggered? • What parameters affect these decisions? Let D be the acceptable range of temp. variation if temp>T+D, turn on Air. Conditioner if temp<T-D, turn on Heater

• Mechanical analogies – Think about how a thermostat does temperature control • What are the actions that can be taken? • What are the conditions under which these actions are triggered? • What parameters affect these decisions? if if temp>T+D, temp<T-D, AC on and HE on and turn on temp<T, temp>T, Air. Conditioner Heater turn AC off turn HE off

• Mechanical analogies – Think about how a thermostat does temperature control • What are the actions that can be taken? • What are the conditions under which these actions are triggered? • What parameters affect these decisions? – Think about how a soda machine works • Keep accepting coins till enough for item • Dispense item (if avail. ), then make change – Think about the decision policy for an elevator – Think about the pattern of traffic signals at an intersection (with sensors) • How do lights depend on cars waiting? Pedestrians?
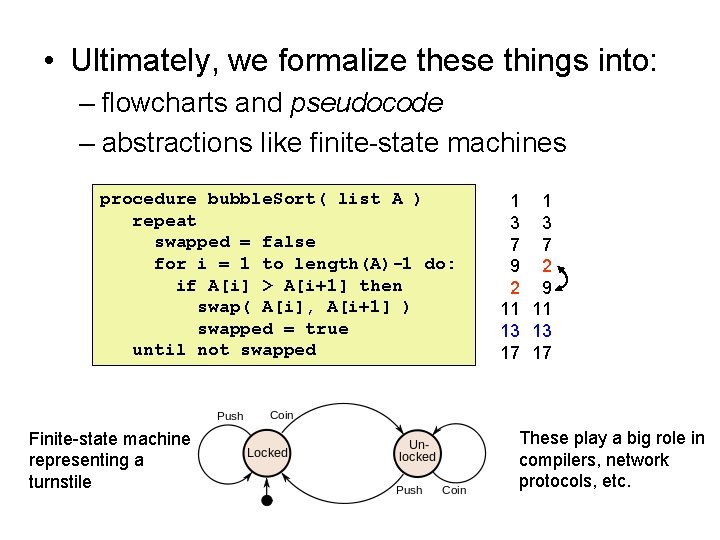
• Ultimately, we formalize these things into: – flowcharts and pseudocode – abstractions like finite-state machines procedure bubble. Sort( list A ) repeat swapped = false for i = 1 to length(A)-1 do: if A[i] > A[i+1] then swap( A[i], A[i+1] ) swapped = true until not swapped Finite-state machine representing a turnstile 1 1 3 3 7 7 9 2 2 9 11 11 13 13 17 17 These play a big role in compilers, network protocols, etc.

The “Earliest” Known Algorithm • Euclid’s algorithm for determining the GCD (greatest common denominator) – also known as the Chinese Remainder Theorem • Problem: given two integers m and n, find the largest integer d that divides each of them • Example: 4 divides 112 and 40; is it the GCD? (no, 8 is)

• Euclid’s algorithm: repeatedly divide the smaller into the larger number and replace with the remainder GCD(a, b): if a<b, swap a and b while b>0: let r be the remainder of a/b a←b, b←r return a 1. 2. 3. 4. a=112, b=40, a/b=2 with rem. 32 a=40, b=32, a/b=1 with rem. 8 a=32, b=8, a/b=4 with rem. 0 a=8, b=0, return 8 • Questions a Computer Scientist would ask: – Does it halt? (note how a always shrinks with each pass). – Is it correct? – Is there a more efficient way to do it (that uses fewer steps)?

. . . UCLA 92 Stanford 80 – Okla. St 55 Iowa 61 – Indiana 83 Mich. St 82. . . • While monitoring a stream of basketball scores, keep track of the 3 highest scores – Impractical to just save them all and sort – How would you do it?

. . . UCLA 92 Stanford 80 – Okla. St 55 Iowa 61 – Indiana 83 Mich. St 82. . . • Algorithm design often starts with representation – Imagine keeping 3 slots, A B C for the highest scores seen so far – Define the “semantics” or an “invariant” to maintain: • A > B > C > all other scores

. . . UCLA 92 Stanford 80 – Okla. St 55 Iowa 61 – Indiana 83 Mich. St 82. . . • Algorithm design often starts with representation – Imagine keeping 3 slots, A B C for the highest scores seen so far – Define the “semantics” or an “invariant” to maintain: • A > B > C > all other scores – With each new game score (p, q) (e. g. Aggies 118, Longhorns 90) if p>A then C=B, B=A, A=p else if p>B, then C=B, B=p else if p>C, then C=p repeat this “shifting” with q p A B A p B A B p

. . . UCLA 92 Stanford 80 – Okla. St 55 Iowa 61 – Indiana 83 Mich. St 82. . . • Algorithm design often starts with representation – Imagine keeping 3 slots, A B C for the highest scores seen so far – Define the “semantics” or an “invariant” to maintain: • A > B > C > all other scores – With each new game score (p, q) (e. g. Aggies 118, Longhorns 90) if p>A then C=B, B=A, A=p else if p>B, then C=B, B=p else if p>C, then C=p repeat this “shifting” with q – Questions to consider: p A B A p B A B p • What happens initially before A, B, and C are defined? • What happens with ties? • Should A, B, and C represent distinct games, or could 2 of them come from the same game?

Spell-checking • Given a document as a list of words, wi, identify misspelled words and suggest corrections – Simple approach: use a dictionary • for each wi, scan dictionary in sorted order – Can you do it faster? (doc size N x dict size D) • Suppose we sort both lists • Sorting algs usually take N log 2 N time – Example: if doc has ~10, 000 words, sort in ~132, 000 steps – Assume you can call a sort sub-routine (reuse of code) – Note: you will learn about different sorting algorithms (and related data structures like trees and hash tables) and analyze their computational efficiency in CSCE 221 • Can scan both lists in parallel (takes D steps) – (D + N log N < ND)
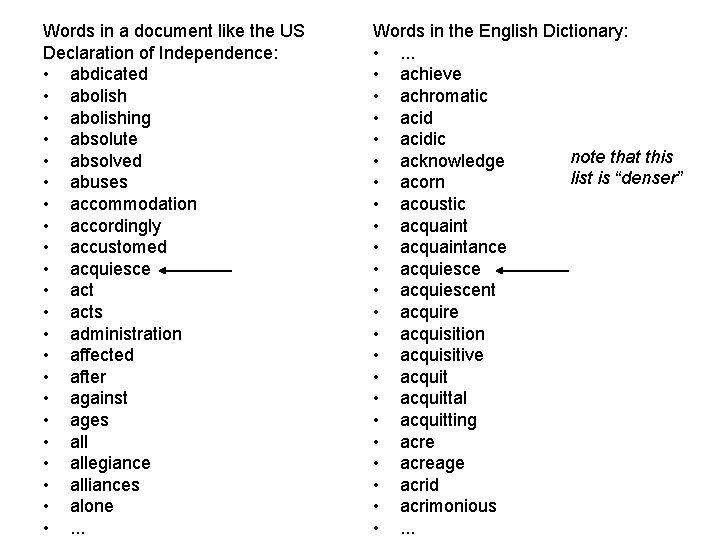
Words in a document like the US Declaration of Independence: • abdicated • abolishing • absolute • absolved • abuses • accommodation • accordingly • accustomed • acquiesce • acts • administration • affected • after • against • ages • allegiance • alliances • alone • . . . Words in the English Dictionary: • . . . • achieve • achromatic • acidic note that this • acknowledge list is “denser” • acorn • acoustic • acquaintance • acquiescent • acquire • acquisition • acquisitive • acquittal • acquitting • acreage • acrid • acrimonious • . . .

• A harder problem: suggesting spelling corrections – Requires defining “closest match” • Fewest different letters? same length? – occupashun occupation – occurence occurrence occupashun ||||||***| d=3 occupation occupashun ||||****** d=6 occurrence occupashun |||***|**| d=5 occl-usion • “Edit distance”: – Formal def: # diff letters + # gap spaces – Minimal dist over all possible gap placements calculated by Dynamic Programming • How to efficiently find all words in dictionary with minimal distance? – Does context matter? • Used as noun or verb (affect vs. effect) • Compliment vs. complement • Principle vs. principal

Summary about Computational Thinking • CT is about transforming (often ill-defined) activities into concrete, well-defined procedures. – A finite sequence of steps anybody could follow, with well-defined decision criteria and termination conditions • Take-home message: the following components are important to computational thinking: 1. 2. 3. 4. 5. Decomposition Identifying patterns and repetition Abstraction and generalization Choosing a representation for the data Defining all decision criteria
- Slides: 22