What is Calculus Calculus involves mathematics that deals

What is Calculus? • Calculus involves mathematics that deals with rates of change that are not constant. • In Algebra, you work with constant rates of change. • In the formula (rate)(time) = (distance), the rate is a constant rate. There is only one problem. . .

A few things move at a constant velocity, but many don’t. . .

Here is a case of a sharp decrease in velocity.

Here, this bungee jumper experiences acceleration, followed by deceleration

Differential Equations: The Study of Rates of Change • In the study of differential equations, we are able to take a rate equation and “solve it”. • To “solve” a differential equation means to write the equation in the form that does not contain rates. • Have you ever heard of “exponential growth”?

Exponential Growth • Exponential Growth occurs when the rate of growth of some “thing”is directly proportional to the amount of that “thing” present. • Example: Plants in a garden grow exponentially. • A possible equation describing this growth could be • dy/dt = 0. 10 y where y = the mass of the plant after “t” days and the plant increases in mass approximately 10% (0. 10) each day. • What is dy/dt?

What is dy/dt? • dy/dt is the “Rate of Growth” of the plant measured in mass units per time. • For example if y = 20 grams, dy/dt = 0. 1(20) = 2 grams of new growth per day. But the next day, the mass of the plant is about 22 grams so, dy/dt = 0. 1(22) = 2. 2 grams of growth and so on. . . • The growth rate keeps growing! What is the solution?

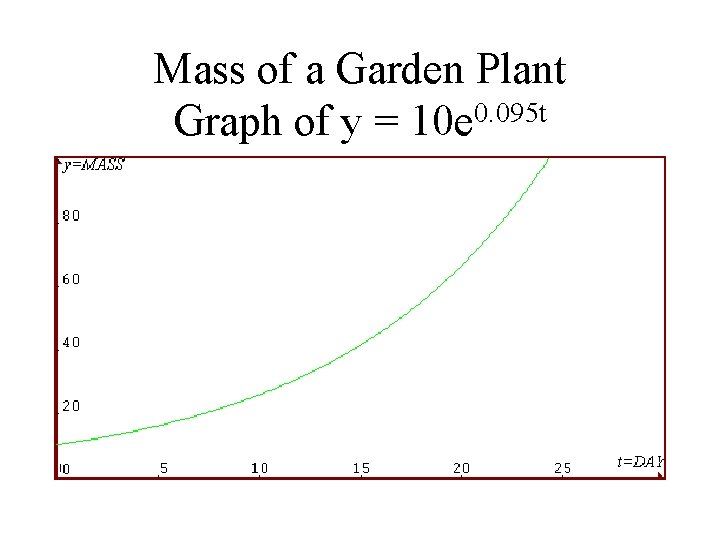
The Solution • Using “techniques” from Calculus, we may “solve” the differential equation dy/dt=0. 10 y to get the equation • y = 10 e 0. 095 t where we use y=10 for day 0. • A “picture” is worth a lot here!

Mass of a Garden Plant Graph of y = 10 e 0. 095 t

How Bad Shocks Affects Car Ride Quality • We can use Calculus and Differential Equations to actually simulate the ride of a car with bad shock absorbers! • In the suspension system of a car, there are two major components: 1) Springs to cushion the ride. 2) Shocks to “dampen” the bounce.

Vertical Acceleration in a Car Ride When Hitting a Bump • When you hit a bump while driving a car, there is a lot of “up and down” change in position and acceleration and deceleration occurring. We use dy/dt to represent the change in position with respect to time and we use d 2 y/dt 2 to represent acceleration.

Equation For This System • The second order differential equation is m* d 2 y/dt 2 + kd*dy/dt + ks*y = 0 where m = mass of rear end of vehicle kd = the damping coefficient due to the shocks ks = the spring coefficient • Note that “damping” is primarily achieved by the shock absorber but additional damping occurs due to frictional heat losses. • After looking up a value for “m” and experimentally determining kd and ks, the equation obtained is 24. 2*d 2 y/dt 2 + 400*dy/dt + 2400*y = 0

Comparison of Solutions Graphed Good Shocks 24. 2*d 2 y/dt 2 + 400*dy/dt + 2400*y = 0 Bad Shocks 24. 2*d 2 y/dt 2 + 200*dy/dt + 2400*y = 0 Very Bad Shocks 24. 2*d 2 y/dt 2 + 100*dy/dt + 2400*y = 0 Note: For this problem, the “solutions” are obtained “graphically”.

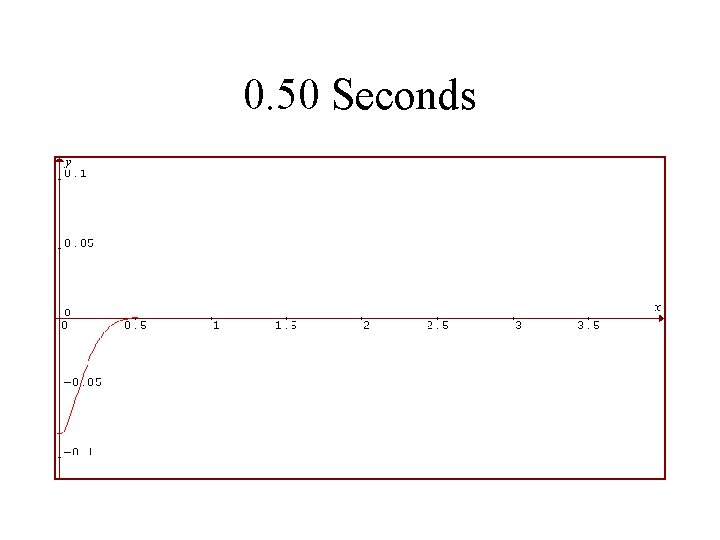
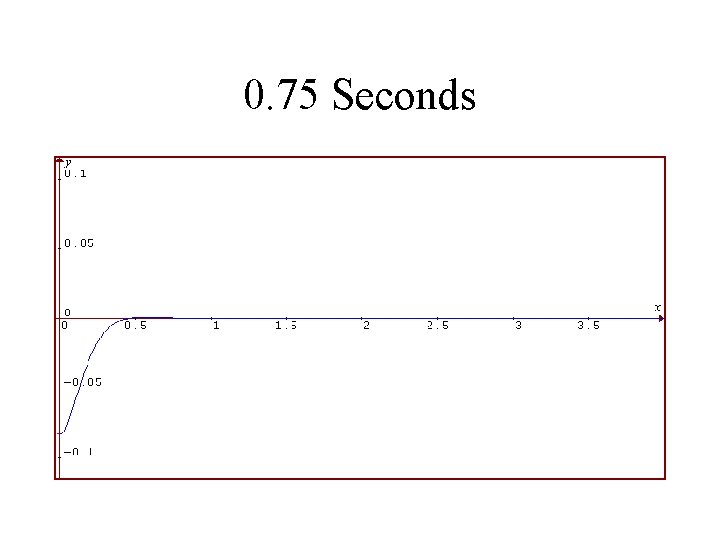
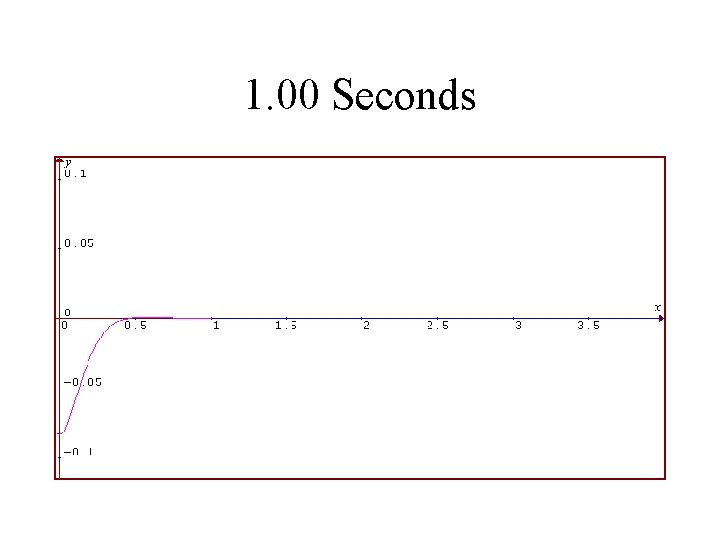
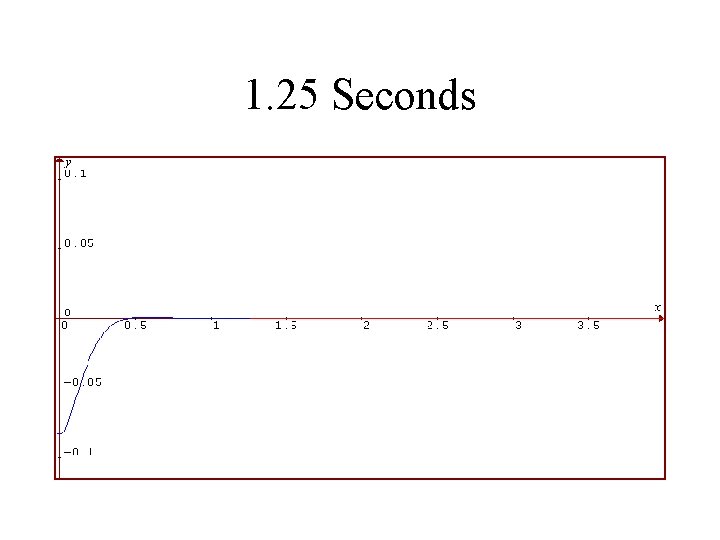
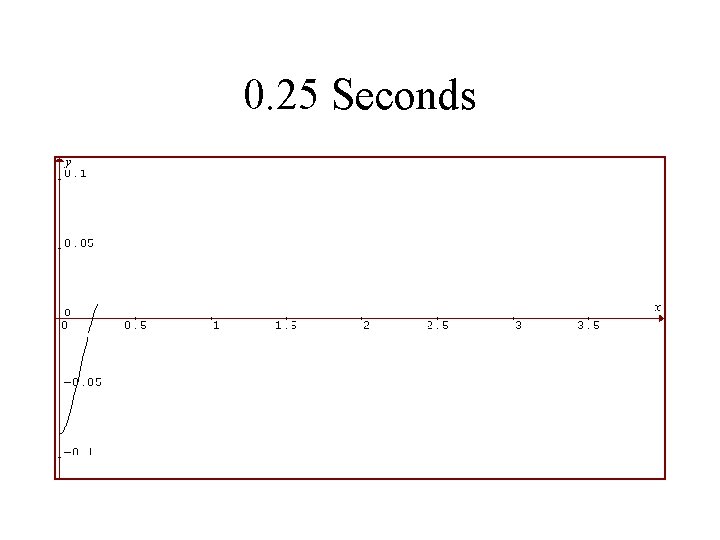
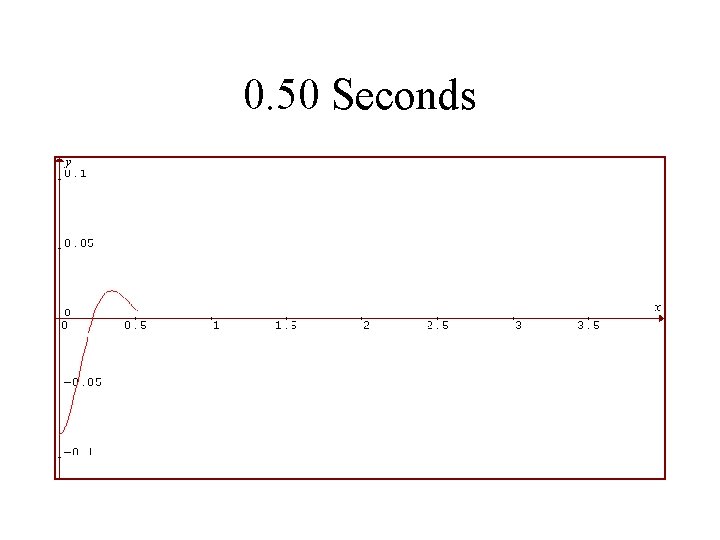
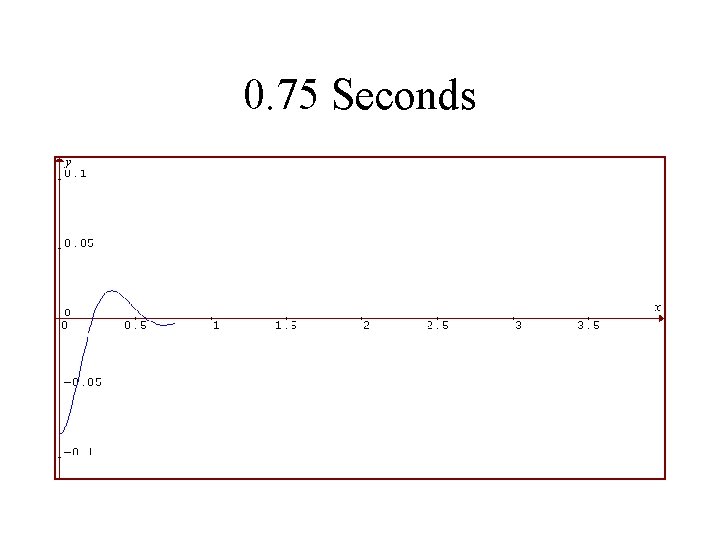
1986 Toyota Celica Suspension System Rear Shocks in Good Condition Vertical Displacement of Rear in Feet is Plotted Against Time in Seconds

0. 25 Seconds

0. 50 Seconds

0. 75 Seconds

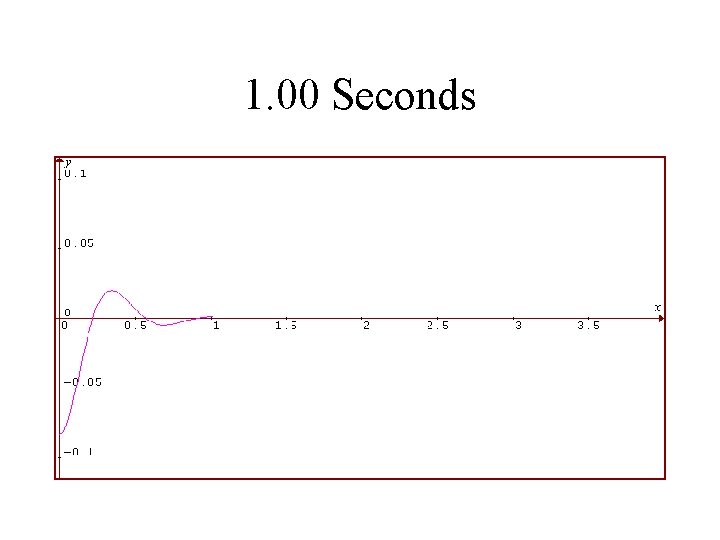
1. 00 Seconds

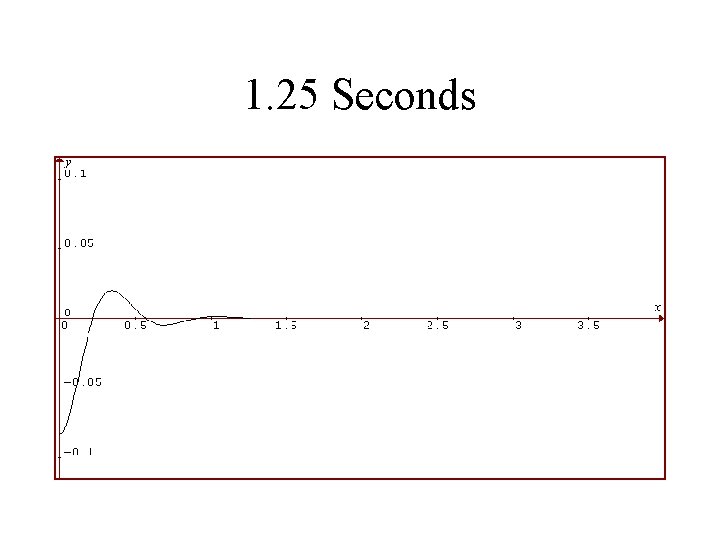
1. 25 Seconds

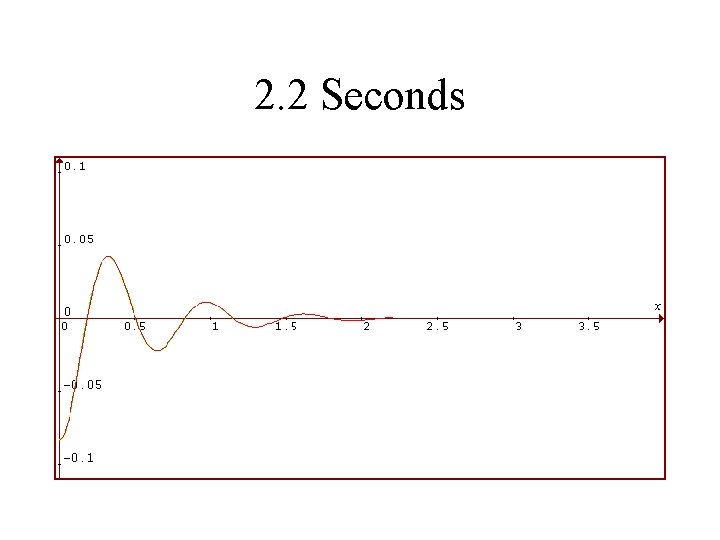
1986 Toyota Celica Suspension System Rear Shocks in BAD Condition Viscosity is 1/2 as Much Vertical Displacement of Rear in Feet is Plotted Against Time in Seconds

0. 25 Seconds

0. 50 Seconds

0. 75 Seconds

1. 00 Seconds

1. 25 Seconds

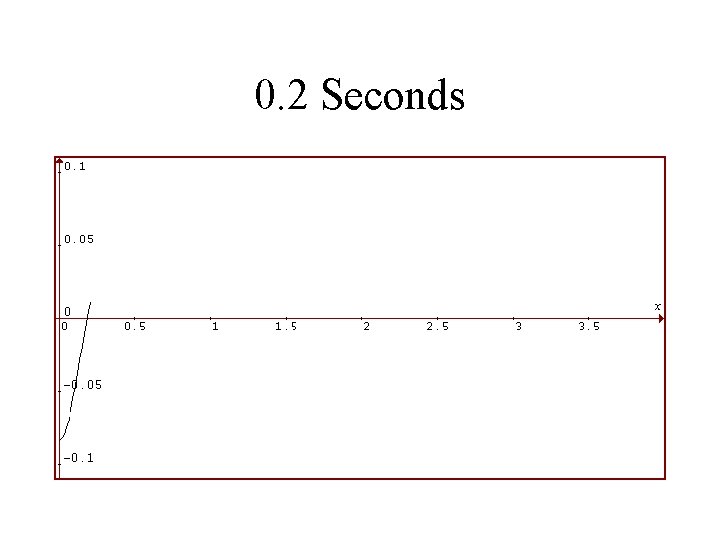
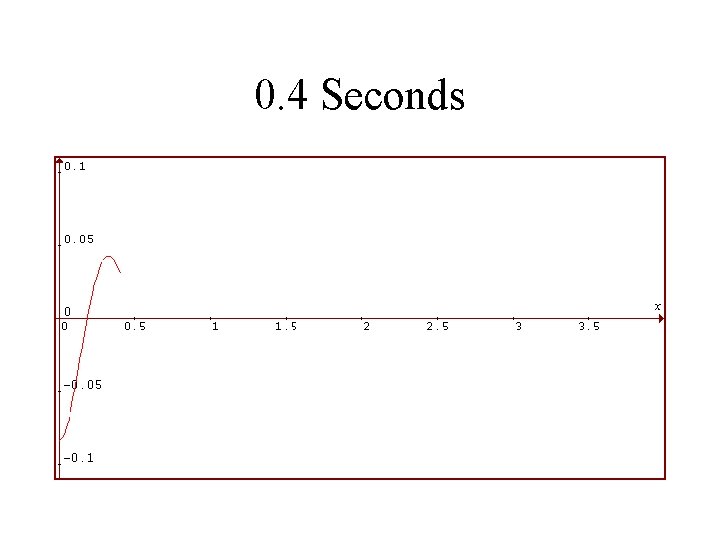
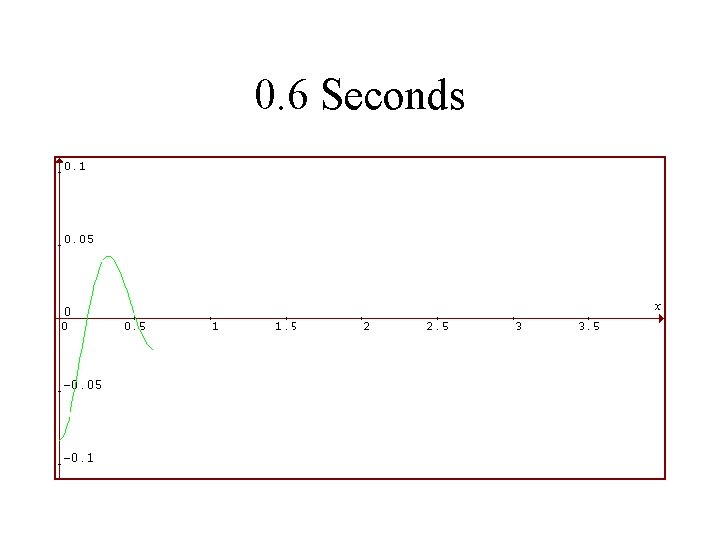
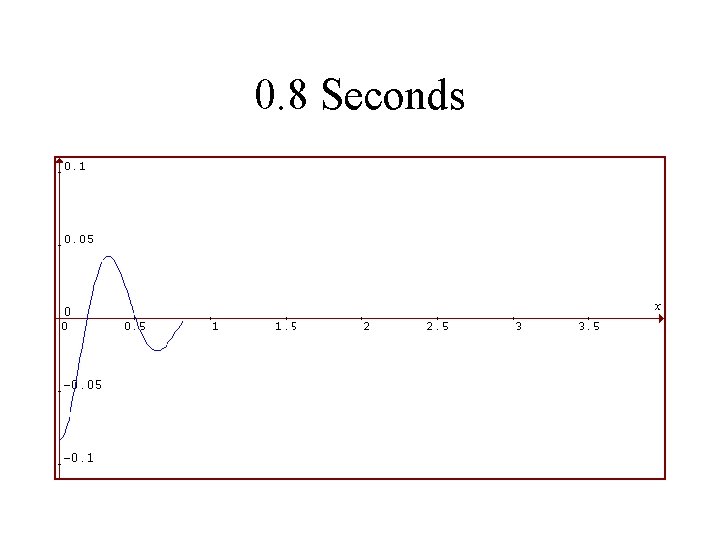
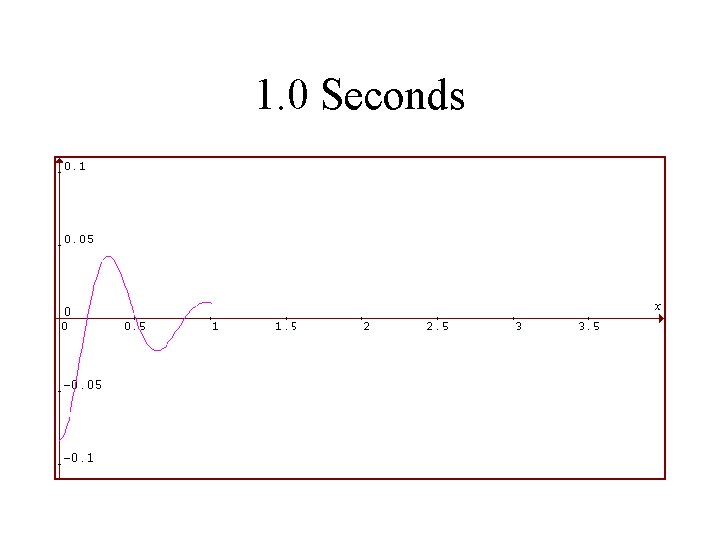
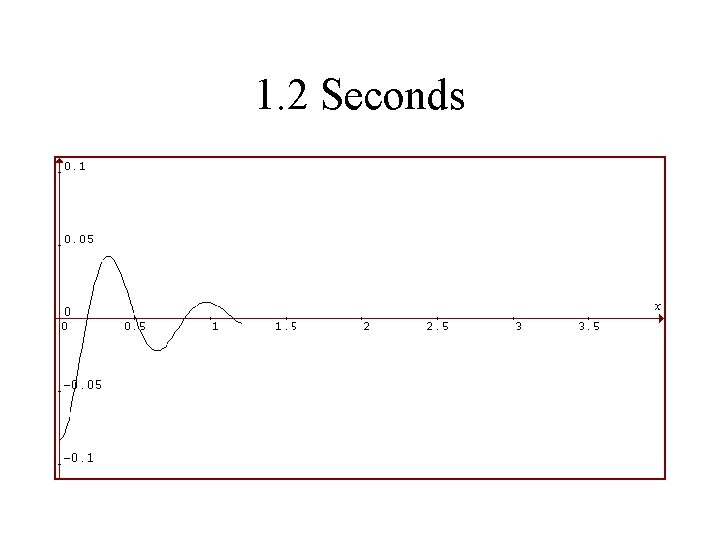
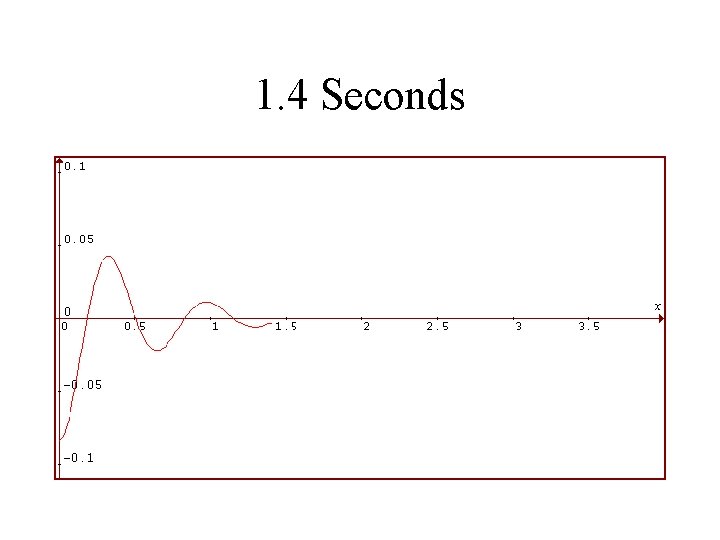
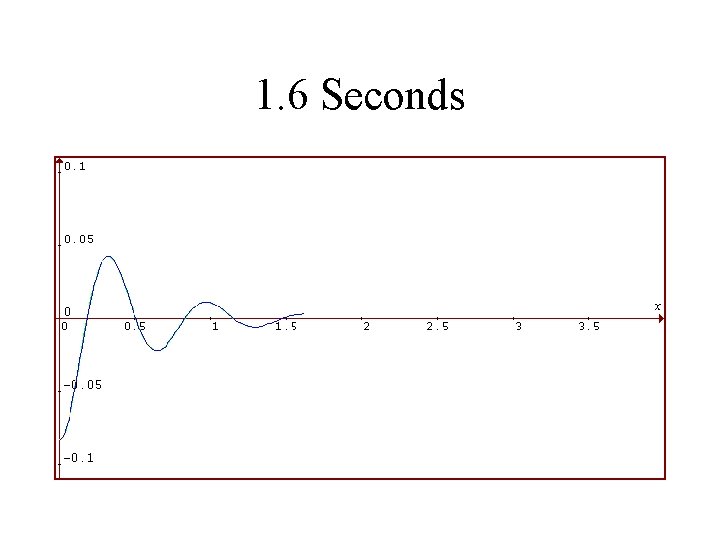
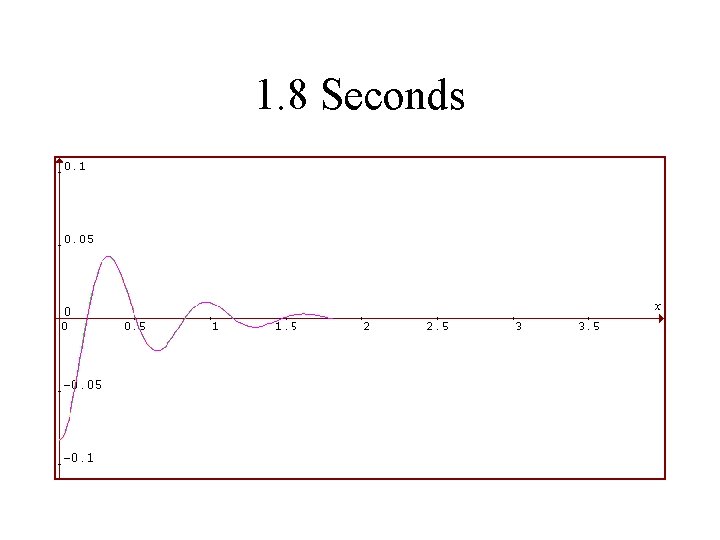
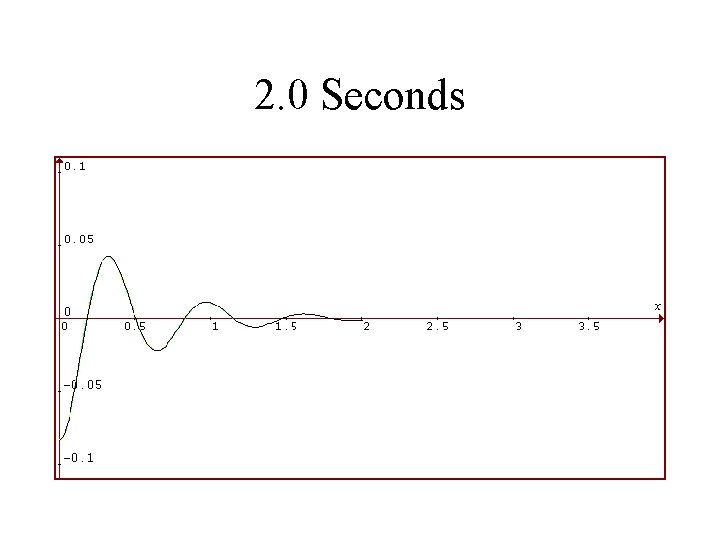
1986 Toyota Celica Suspension System Rear Shocks in VERY BAD Condition Viscosity is 1/4 as Much Vertical Displacement of Rear in Feet is Plotted Against Time in Seconds

0. 2 Seconds

0. 4 Seconds

0. 6 Seconds

0. 8 Seconds

1. 0 Seconds

1. 2 Seconds

1. 4 Seconds

1. 6 Seconds

1. 8 Seconds

2. 0 Seconds

2. 2 Seconds