What is astronomy Greek word astronomia Asteri star

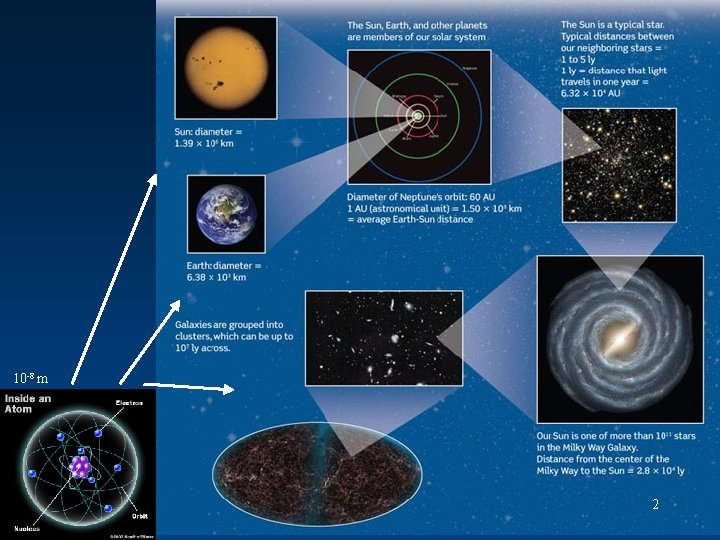
What is astronomy? • Greek word astronomia – Asteri = star – Nomos = law, principle, act • The study of the cosmos (at all scales). What scales are relevant to astronomy? 1

10 -8 m 2

How astronomy works In astronomy, we make observations and measurements: Angles, Motions, Morphologies, Brightnesses, Spectra Etc. We interpret and explain in terms of physics: Mechanics, atomic and molecular processes, radiation properties thermodynamic properties, etc. Through which we learn about nature and history of the cosmos: Structure and evolution of stars, galaxies, galaxy clusters, origin and expansion of the universe Our theories in turn motivate the next observations, thus our understanding is continually being refined. 3

Angles, Powers of Ten, Units in Astronomy 4

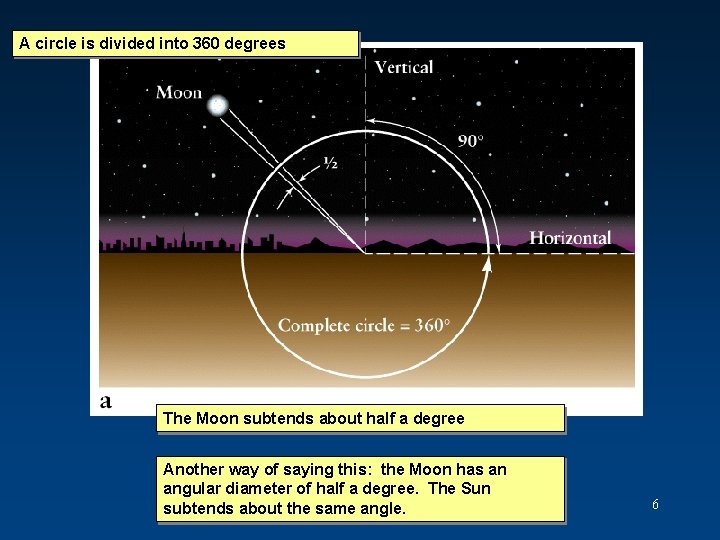
Angles Astronomers use angular measure to describe: • • the locations of celestial objects on the sky the apparent size of an object separation between objects movement of objects on the sky (later: to convert to actual sizes, separations, motions, must know distance to object!) 5

A circle is divided into 360 degrees The Moon subtends about half a degree Another way of saying this: the Moon has an angular diameter of half a degree. The Sun subtends about the same angle. 6

How to estimate angles Extend your arm, and use your hand fingers like this: Is this what you expected for the Moon’s angular diameter? 7

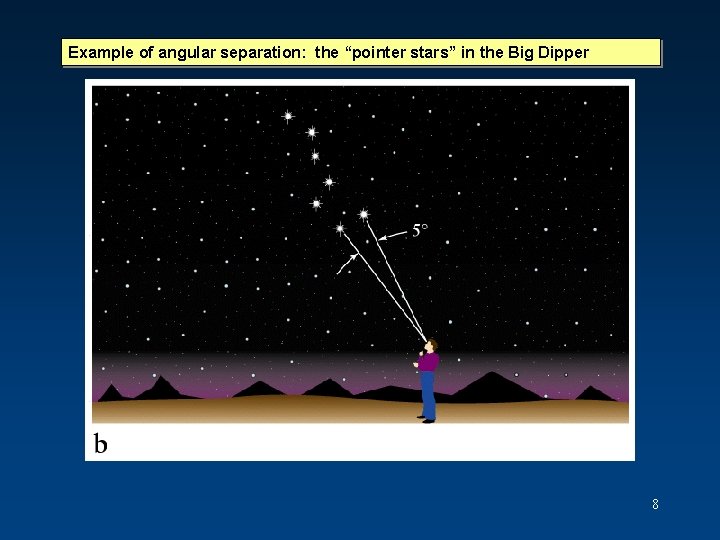
Example of angular separation: the “pointer stars” in the Big Dipper 8

How do we express smaller angles? We subdivide the degree into 60 arcminutes (a. k. a. minutes of arc): 1 = 60 arcmin = 60’ An arcminute is split into 60 arcseconds (a. k. a. seconds of arc): 1’ = 60 arcsec = 60” An arcsecond is split into 1000 milli-arcseconds (yes, we need these) 9

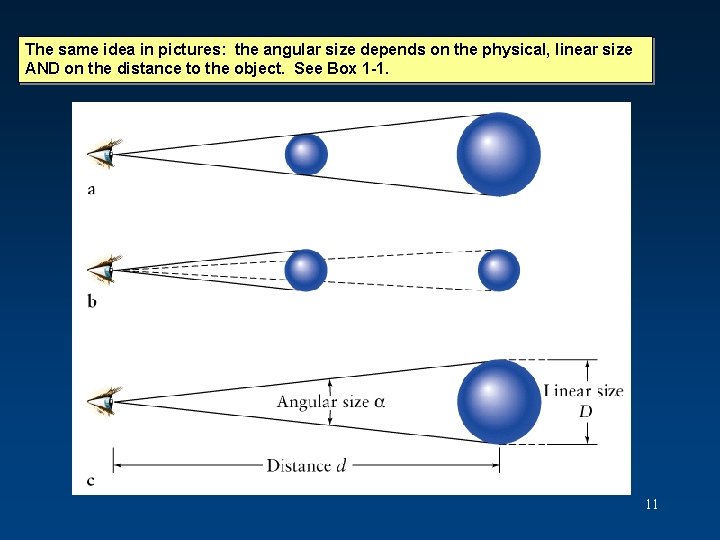
The small-angle formula Relation between angular size, physical size, and distance to an object: where D = linear size of an object a = angular size of the object (in arcsec) d = distance to the object (in same units as D) 206, 265 is the number of arcseconds in a circle divided by 2 (i. e. it is the number of arcseconds in a radian). Where does this formula come from? 10

The same idea in pictures: the angular size depends on the physical, linear size AND on the distance to the object. See Box 1 -1. 11

Examples The Moon is at a distance of about 384, 000 km. If it subtends 0. 5°, from the small-angle formula, its diameter is about 3400 km. The resolution of your eye is about 1’. What length can you resolve at a distance of 10 m? 12

Powers-of-ten notation • Astronomy deals with very big and very small numbers – we talk about galaxies AND atoms! • Example: distance to the Sun is about 150, 000, 000 meters. Inconvenient to write! • Use “powers-of-ten”, or “exponential notation”. All the zeros are consolidated into one term consisting of 10 followed by an exponent, written as a superscript. Eg. , 150, 000, 000 = 1. 5 x 1011 13

Examples: powers-of-ten notation 100 = 10 x 10 = 102 150 = 1. 5 x 100 = 1. 5 x 102 84, 500, 000 = 8. 45 x 107 10 -2 = 1/100 0. 032 = 3. 2/100 = 3. 2 x 10 -2 0. 0000045 = 4. 5 x 10 -6 14

Arithmetic with powers-of-ten notation To multiply numbers, add exponents: Examples: 10 x 100 = 101 x 102 = 1000 = 10 x 10 = 103 (2 x 104) x (3 x 105) = (2 x 3) x 104+5 = 6 x 109 To divide numbers, subtract exponents: Example: (6 x 106) / (3 x 104) = (6/3) x 106 -4 = 2 x 102 15

Some familiar numbers in powers-of-ten notation: prefix One thousand = 1000 = 103 One million = 1, 000 = 106 One billion = 1, 000, 000 = 109 kilo mega giga One one-hundredth = 0. 01 = 10 -2 One one-thousandth = 0. 001 = 10 -3 One one-millionth = 0. 000001= 10 -6 centi milli micro 16

Important note on Significant Figures A significant figure is any digit in a number when it is written in scientific notation. For example, 3. 14159 = 3. 14159 x 100, has six significant figures but so does 0. 0000314159 = 3. 14159 x 10 -5. 2. 850 has four significant figures, but 2. 85 has only three. The last zero is telling you that digit is not 1 or something else, but 2. 85 could be representing 2. 851, rounded off. It is important in calculations to keep only significant figures, e. g. 1. 2/1. 1 = 1. 1, even though calculator says 1. 09090909…, the input numbers were only know to 1 sig fig, so the answer is too. 17

Units in astronomy Every physical quantity has units associated with it (don’t ever leave them off!). Astronomers use the metric system, • distances in meters • masses in kg • time in s • temperature in °C or K and a few special units (see later). 18

Size estimate Atom: 10 -8 m 19

Size estimate Child: 100 m 20

Size estimate Earth: 107 m 21

Size estimate Sun: 109 m 22

Size estimate Galaxy: 1021 m 23

Size estimate The visible Universe: 1026 m 24

Special distance units: light-year • A light-year is the distance the light travels in one year. Speed of light is 3 x 108 m/s. In one year, light travels about 9. 5 x 1015 m. NB: a distance, not a time. • Example, light takes 4. 22 years to travel from Earth to Proxima Centauri, the nearest star beyond the solar system => Proxima Centauri is 4. 22 light-years away. • Hence we see this star as it was 4. 22 years ago. 25

The visible Universe • If the Universe is 13. 8 Gyr old, we cannot know anything about objects for which the light would have had to travel more than 13. 8 billion lightyears to get to us (those signals have not yet had enough time to reach us) R~13. 8 billion lyr …all objects whose light has traveled less than 13. 8 billion light-years to reach us. 26

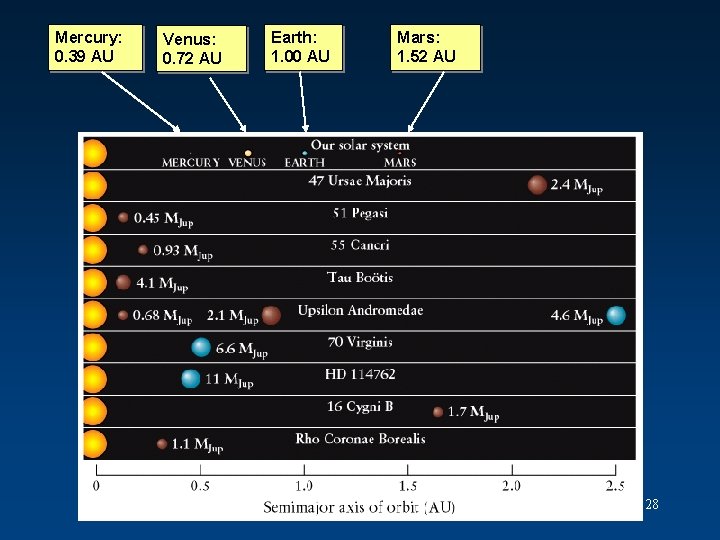
The Astronomical Unit (AU) 1 Astronomical Unit = 1 AU = the average distance between the Earth and the Sun = 1. 496 x 108 km. Why? It’s convenient for interplanetary distances! Example: The average distance between Jupiter and the Sun is 5. 2 AU. Isn’t that simpler than 7. 8 x 108 km ? 27

Mercury: 0. 39 AU Venus: 0. 72 AU Earth: 1. 00 AU Mars: 1. 52 AU 28

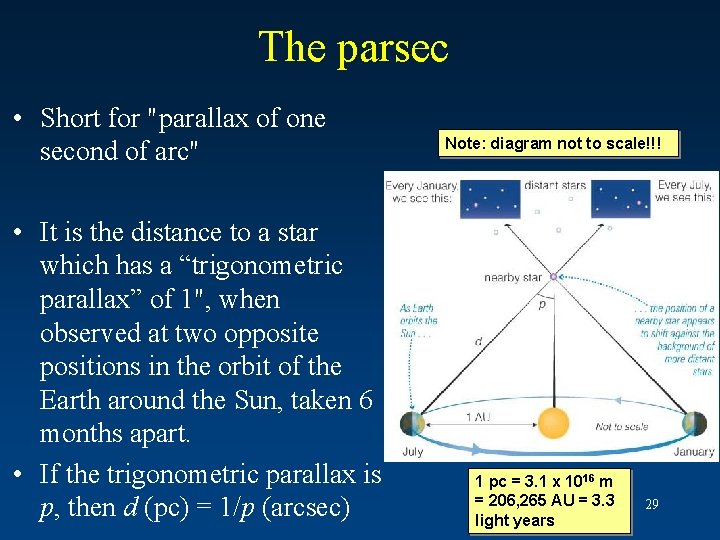
The parsec • Short for "parallax of one second of arc" • It is the distance to a star which has a “trigonometric parallax” of 1", when observed at two opposite positions in the orbit of the Earth around the Sun, taken 6 months apart. • If the trigonometric parallax is p, then d (pc) = 1/p (arcsec) Note: diagram not to scale!!! 1 pc = 3. 1 x 1016 m = 206, 265 AU = 3. 3 light years 29

30