What is Algorithm Complexity 2 3 Algorithm Complexity

What is Algorithm Complexity? 2. 3 Algorithm Complexity The algorithmic complexity of a computation is some measure of how difficult it is to perform the computation. (문제 계산(computation)이 얼마나 어려운가를 나타내는 측정치이다. ) Measures some aspect of cost of computation (in a general sense of cost). (계산을 위한 비용에 대한 측정치이다. ) Common complexity measures: • Time complexity: # of operations or steps required • Space complexity: # of memory bits required Page 2 Discrete Mathematics by Yang-Sae Moon

Complexity Depends on Input 2. 3 Algorithm Complexity Most algorithms have different complexities for inputs of different sizes. (E. g. searching a long list takes more time than searching a short one. ) (대부분의 알고리즘은 입력의 크기에 따라 복잡도가 달라진다. 당연!) Therefore, complexity is usually expressed as a function of input length. (따라서, 복잡도는 입력의 크기/길이에 대한 함수로 표현한다. ) This function usually gives the complexity for the worstcase input of any given length. (복잡도를 나타내는 함수는 통상 입력 크기가 최악인 경우를 고려한다. ) Page 3 Discrete Mathematics by Yang-Sae Moon

Example: Max Algorithm 2. 3 Algorithm Complexity procedure max(a 1, a 2, …, an: integers) v : = a 1 {largest element so far} for i : = 2 to n {go thru rest of elems} if ai > v then v : = ai {found bigger? } {at this point v’s value is the same as the largest integer in the list} return v Problem: Find the exact order of growth ( ) of the worstcase time complexity of the max algorithm. Assume that each line of code takes some constant time every time it is executed. Page 4 Discrete Mathematics by Yang-Sae Moon

Complexity Analysis of Max Algorithm (1/2) 2. 3 Algorithm Complexity procedure max(a 1, a 2, …, an: integers) v : = a 1 t 1 for i : = 2 to n t 2 if ai > v then v : = ai return v t 3 t 4 Times for each execution of each line. (각 line을 하나의 수행으로 볼 때의 시간) What’s an expression for the exact total worst-case time? (Not its order of growth. ) (최악의 경우, 정확한 수행 시간을 어떻게 될까? ) Page 5 Discrete Mathematics by Yang-Sae Moon

Complexity Analysis of Max Algorithm (2/2) 2. 3 Algorithm Complexity procedure max(a 1, a 2, …, an: integers) v : = a 1 t 1 for i : = 2 to n t 2 if ai > v then v : = ai t 3 return v t 4 Times for each execution of each line. (각 line을 하나의 수행으로 볼 때의 시간) Worst case execution time: Page 6 Discrete Mathematics by Yang-Sae Moon

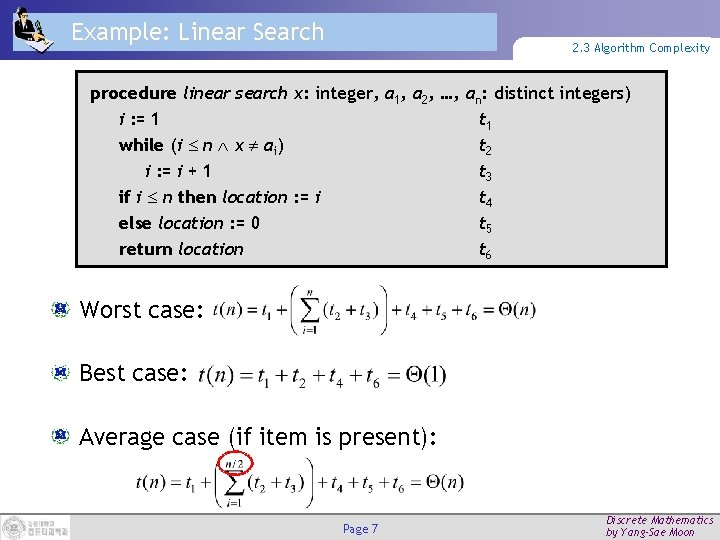
Example: Linear Search 2. 3 Algorithm Complexity procedure linear search x: integer, a 1, a 2, …, an: distinct integers) i : = 1 t 1 while (i n x ai) t 2 i : = i + 1 t 3 if i n then location : = i t 4 else location : = 0 t 5 return location t 6 Worst case: Best case: Average case (if item is present): Page 7 Discrete Mathematics by Yang-Sae Moon

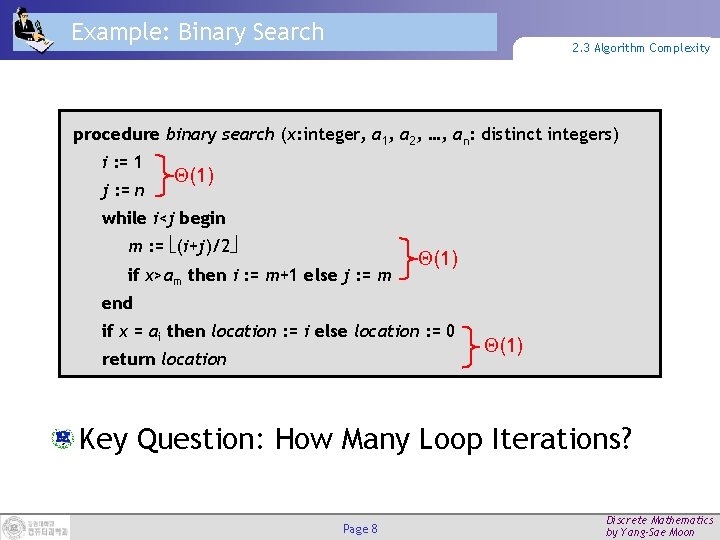
Example: Binary Search 2. 3 Algorithm Complexity procedure binary search (x: integer, a 1, a 2, …, an: distinct integers) i : = 1 j : = n (1) while i<j begin m : = (i+j)/2 if x>am then i : = m+1 else j : = m (1) end if x = ai then location : = i else location : = 0 return location (1) Key Question: How Many Loop Iterations? Page 8 Discrete Mathematics by Yang-Sae Moon

Binary Search Analysis 2. 3 Algorithm Complexity Suppose n=2 k. Original range from i=1 to j=n contains n elements. Each iteration: Size j i+1 of range is cut in half. (매번 검색 범위(j-i+1)의 절반(½)씩 줄여 나간다. ) Loop terminates when size of range is 1=20 (i=j). (검색 범위의 변화: 2 k 2 k-1 2 k-2 … 21 20, 결국 반복 횟수 = k) Therefore, number of iterations is k = log 2 n = (log 2 n)= (log n) (반복 횟수 = k이고, log 2 n = log 22 k이므로…) Even for n 2 k (not an integral power of 2), time complexity is still (log 2 n) = (log n). Page 9 Discrete Mathematics by Yang-Sae Moon

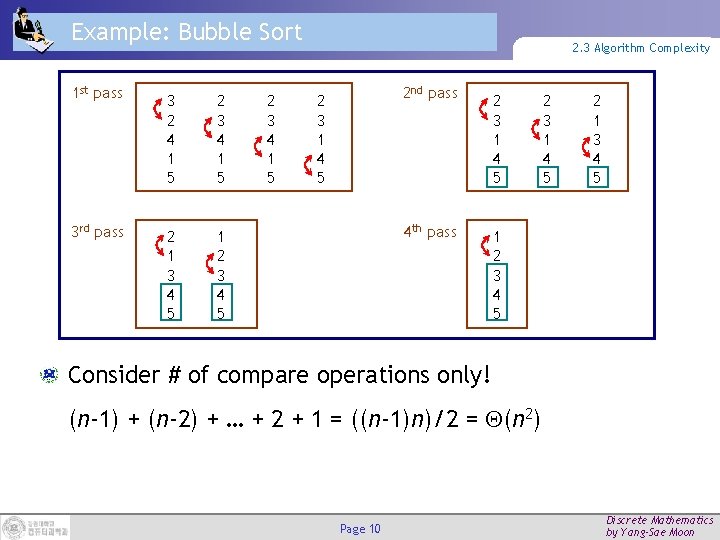
Example: Bubble Sort 1 st pass 3 2 4 1 5 2 3 4 1 5 3 rd pass 2 1 3 4 5 1 2 3 4 5 2 3 4 1 5 2. 3 Algorithm Complexity 2 3 1 4 5 2 nd pass 2 3 1 4 5 4 th pass 1 2 3 4 5 2 3 1 4 5 2 1 3 4 5 Consider # of compare operations only! (n-1) + (n-2) + … + 2 + 1 = ((n-1)n)/2 = (n 2) Page 10 Discrete Mathematics by Yang-Sae Moon

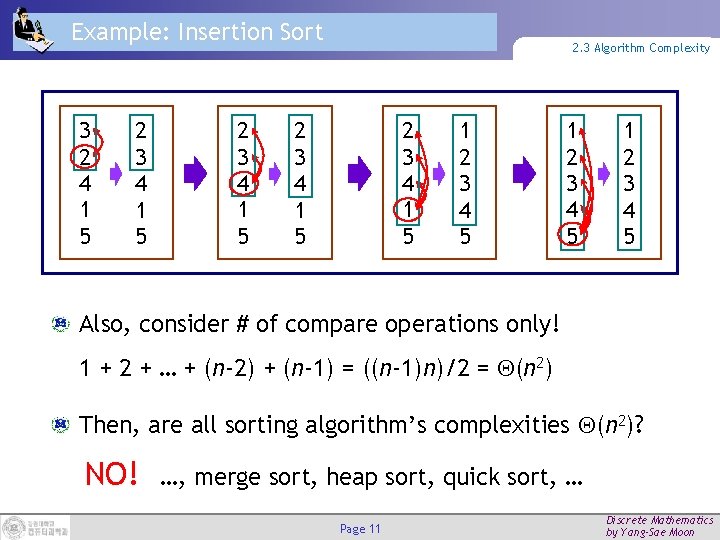
Example: Insertion Sort 3 2 4 1 5 2 3 4 1 5 2. 3 Algorithm Complexity 2 3 4 1 5 1 2 3 4 5 Also, consider # of compare operations only! 1 + 2 + … + (n-2) + (n-1) = ((n-1)n)/2 = (n 2) Then, are all sorting algorithm’s complexities (n 2)? NO! …, merge sort, heap sort, quick sort, … Page 11 Discrete Mathematics by Yang-Sae Moon

Names for Some Orders of Growth (1) Constant (log n) Logarithmic (n) Linear (n log n) Polylogarithmic (nc) Polynomial (cn), c>1 Exponential (n!) Factorial Page 12 2. 3 Algorithm Complexity Discrete Mathematics by Yang-Sae Moon

Tractable versus Intractable 2. 3 Algorithm Complexity A problem or algorithm with at most polynomial time complexity is considered tractable (or feasible). P is the set of all tractable problems. (Polynomial 복잡도를 가지면, 풀만한(풀기 쉬운) 문제라 여기며, 이러한 문제들 의 집합을 P라 나타낸다. ) A problem or algorithm that has more than polynomial complexity is considered intractable (or infeasible). (Polynomial 복잡도 이상이면 풀기 어려운 문제라 여긴다. ) But, note that • n 1, 000 is technically tractable, but really impossible. • clog log n is technically intractable, but easy. Page 13 Discrete Mathematics by Yang-Sae Moon

Unsolvable Problems 2. 3 Algorithm Complexity Alan Turing discovered in the 1930’s that there are problems unsolvable by any algorithm. (튜링은 “어떠한 알고리즘으로도 풀 수 없는 문제가 있음”을 밝혔다. ) Example: the halting problem. • Given an arbitrary algorithm and its input, will that algorithm eventually halt, or will it continue forever in an “infinite loop? ” (주어진 알고리즘이 결국 정지하는지의 여부를 판단하는 문제는 결국 풀 수가 없다. ) Page 14 Discrete Mathematics by Yang-Sae Moon

P versus NP (1/3) 2. 3 Algorithm Complexity P is the set of all tractable problems. (i. e. , the problems have at most polynomial time complexity. ) (통상적으로 polynomial complexity를 가지면 P이다. ) NP is the set of problems for which there exists a tractable algorithm for checking solutions to see if they are correct. • In other words, NP is the set of decision problems for which a given proposed solution for a given input can be checked quickly (in polynomial time) to see if it really is a solution. • 주어진 입력에 대해 제시된 솔루션이 바른 해인지의 여부를 빠르게(polynomial time) 판단할 수 있는 알고리즘이 존재하는 문제들의 집합이 NP이다. • 통상적으로 exponential/factorial complexity를 가지면 NP이다. Page 15 Discrete Mathematics by Yang-Sae Moon

P versus NP (2/3) - skip 2. 3 Algorithm Complexity NP-complete is the term used to describe decision problems that are the hardest ones in NP in the sense that, if there were a polynomialbounded algorithm for an NP complete problem, then there would be a polynomial-bounded algorithm for each problem in NP. • NP중에서도 어려운 문제들이란 용어를 의미하며, 하나의 NP-complete 문제가 풀리면 (P가 되면), 관련된 수많은 모든 NP-complete 문제가 동시에 풀리게 된다. • 많은 학자들은 어려운 많은 문제들에 대해서 NP-complete임을 증명(특정 문제가 다른 NP-complete 문제로 해석(변경)될 수 있음을 보임)하였다. Page 16 Discrete Mathematics by Yang-Sae Moon

P versus NP (3/3) - skip 2. 3 Algorithm Complexity We know P NP, but the most famous unproven conjecture in computer science is that this inclusion is proper (i. e. , that P NP rather than P=NP). Whoever first proves it will be famous! Page 17 Discrete Mathematics by Yang-Sae Moon

Computer Time Examples #ops(n) log 2 n n n log 2 n n 2 2 n n=10 3. 3 ns 10 ns 33 ns 100 ns 1. 024 s n=106 19. 9 ns 1 ms 19. 9 ms 16 m 40 s 10301, 004. 5 Gyr n! 3. 63 ms Ouch! 2. 3 Algorithm Complexity Assume time = 1 ns (10 9 second) per operation You should carefully design algorithms and write programs! Page 18 Discrete Mathematics by Yang-Sae Moon

Homework #3 2. 3 Algorithm Complexity Page 19 Discrete Mathematics by Yang-Sae Moon