What is a Vector AB and CD have

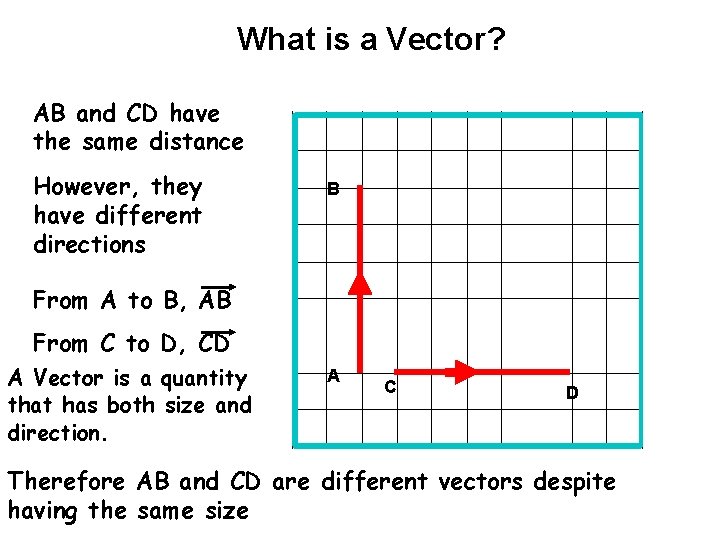
What is a Vector? AB and CD have the same distance However, they have different directions B From A to B, AB From C to D, CD A Vector is a quantity that has both size and direction. A C D Therefore AB and CD are different vectors despite having the same size

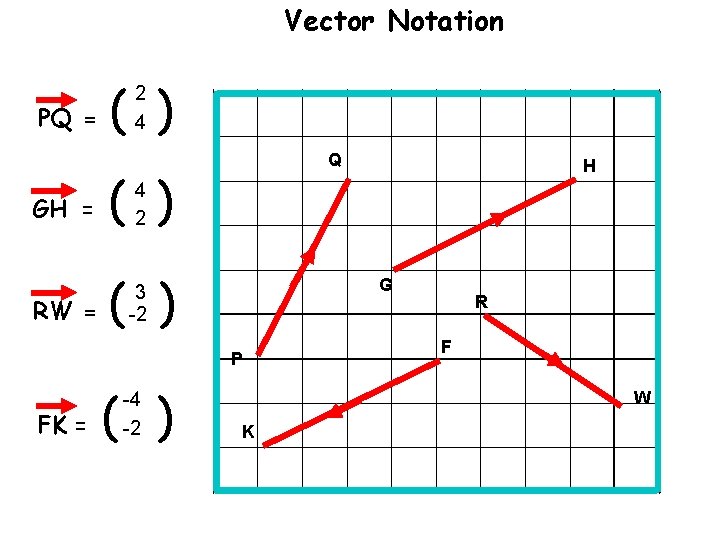
Vector Notation PQ = ( ) 2 4 GH = ( ) RW = ( ) Q 4 2 G 3 -2 P FK = H ( ) -4 -2 R F W K

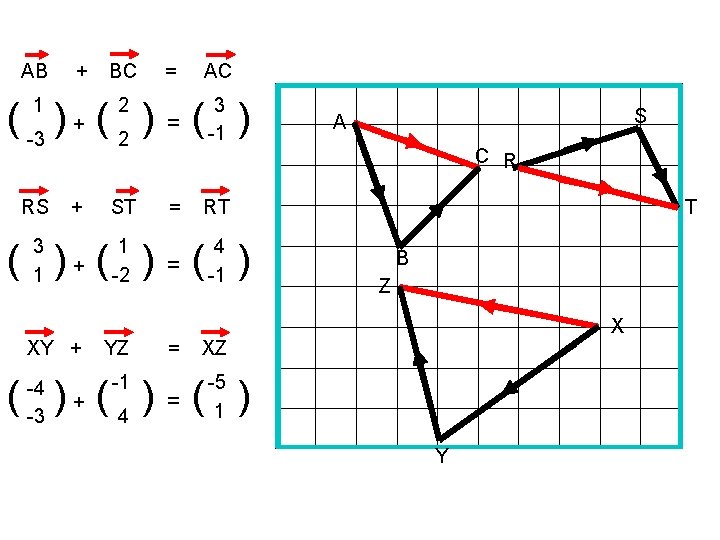
Addition of Vectors RT = (-2 ) TS = ( ) 5 S -1 6 You can add these column vectors to find RS by adding the corresponding points R T The diagram shows RT + TS = RS ( ) 5 -2 + ( )=( -1 6 5 + -1 -2 + 6 ) = ( ) 4 4

B can also be written as a small letter The vector AB a A a a a -a If vectors are the same size and have the same direction they can be labelled with the same letter If there are two vectors of the same size but one is going in the opposite direction you can indicate this by putting a negative sign in front of the letter

Subtraction of Vectors 3 -4 -4 p= ( ) q= ( -5 ) So we get p + -q or p - q p-q To find p – q subtract the corresponding points p-q = = 3 -4 -4 ( ) - ( -5 ) ( 3 - -4 -4 - -5 7 1 ( ) ) p -qq =

Multiplying a Vector by a Scalar The diagram shows that the vector a has been multiplied by a scalar 2 to get 2 a a= 3 3 ( ) 2 a = ( 2 x 3 a 6 6 2 a )=( ) -½a The vector a has been multiplied by a scalar - ½. This means that - ½ a is half as long as a and in the opposite direction. So we get …. . -½x 3 -½a= -½x 3 ( )=( -1 ½ )

6 s = ( -2 ) t = Write the following as column Vectors: a) 2 s b) - t c) -3 t d) - ½ s e) s – t f) 3 t – s g) -4(2 t – 3 s) ( -3 4 )

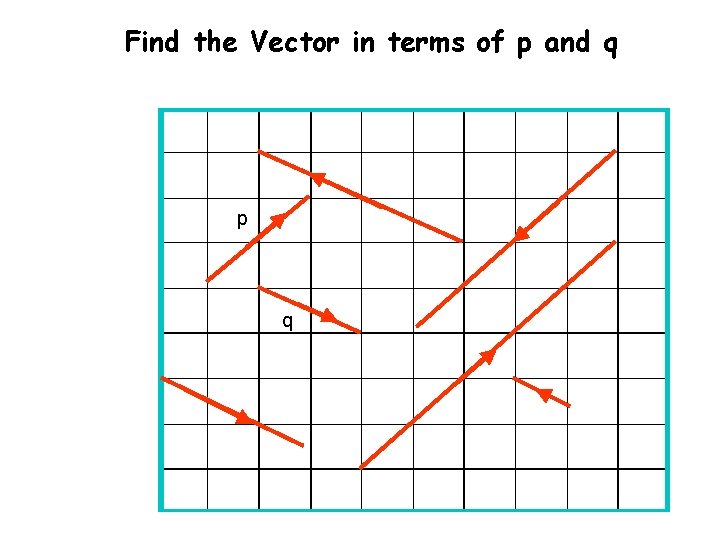
Find the Vector in terms of p and q p q

The vector PQ = q – p Q Finding the midpoint of PQ …… OM = p + ½ PQ M q P = p + ½ (q – p) p =p+½q–½p =½p+½q = ½ (p + q) O

OA = 4 p + 3 q and OB = 3 p -2 q B M A Find AB in terms of p and q AB = - (4 p + 3 q) + 3 p – 2 q AB = -4 p – 3 q + 3 p – 2 q AB = -p - 5 q Find the position vector of the midpoint of AB Position vector of midpoint of AB is ½ (a + b) = ½ [(4 p + 3 q) + (3 p – 2 q)] = ½ [ 7 p + q ] O

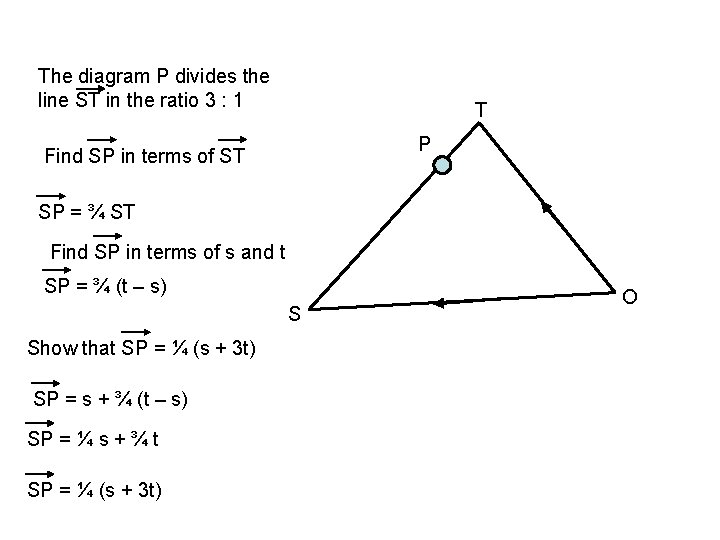
The diagram P divides the line ST in the ratio 3 : 1 T P Find SP in terms of ST SP = ¾ ST Find SP in terms of s and t SP = ¾ (t – s) S Show that SP = ¼ (s + 3 t) SP = s + ¾ (t – s) SP = ¼ s + ¾ t SP = ¼ (s + 3 t) O

C F G B A K H M E N J L