What is a Truss A structure composed of

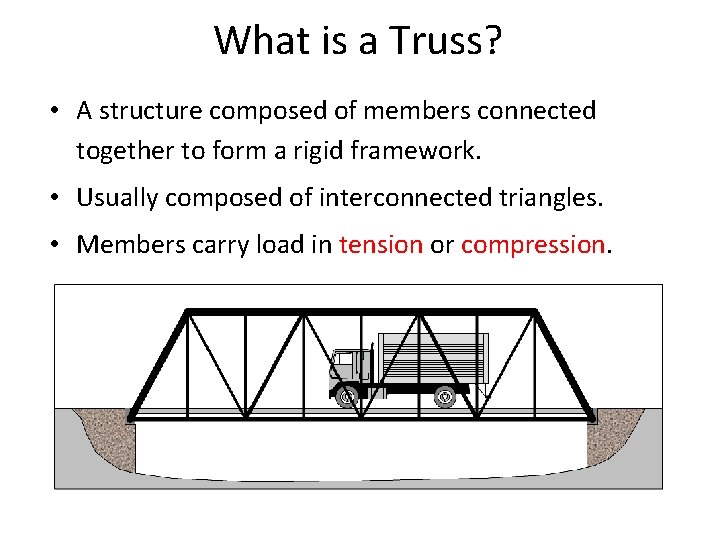
What is a Truss? • A structure composed of members connected together to form a rigid framework. • Usually composed of interconnected triangles. • Members carry load in tension or compression.

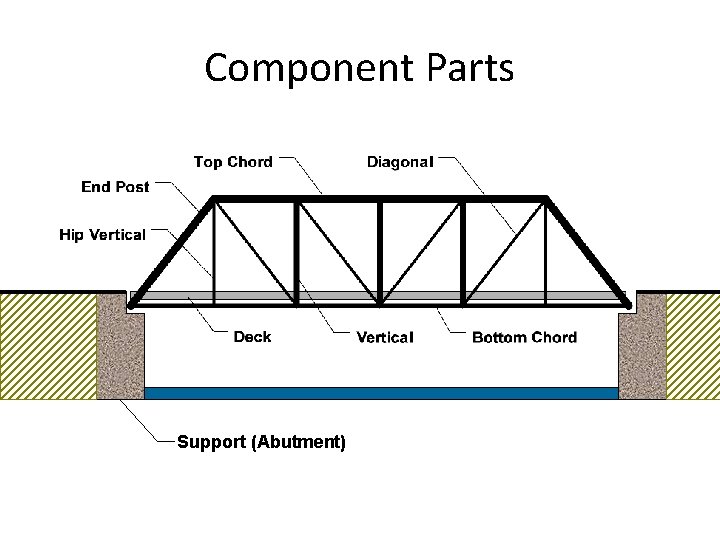
Component Parts Support (Abutment)

Standard Truss Configurations

Types of Structural Members These shapes are called cross-sections.

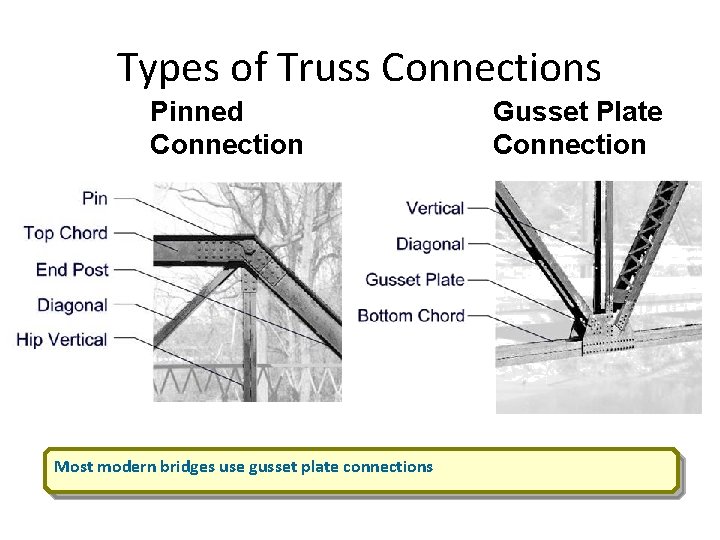
Types of Truss Connections Pinned Connection Most modern bridges use gusset plate connections Gusset Plate Connection

Forces, Loads, & Reactions • Force – A push or pull. • Load – A force applied to a structure. Self-weight of structure, weight of vehicles, pedestrians, snow, wind, etc. • Reaction – A force developed at the support of a structure to keep that structure in equilibrium. Forces are represented mathematically as VECTORS.

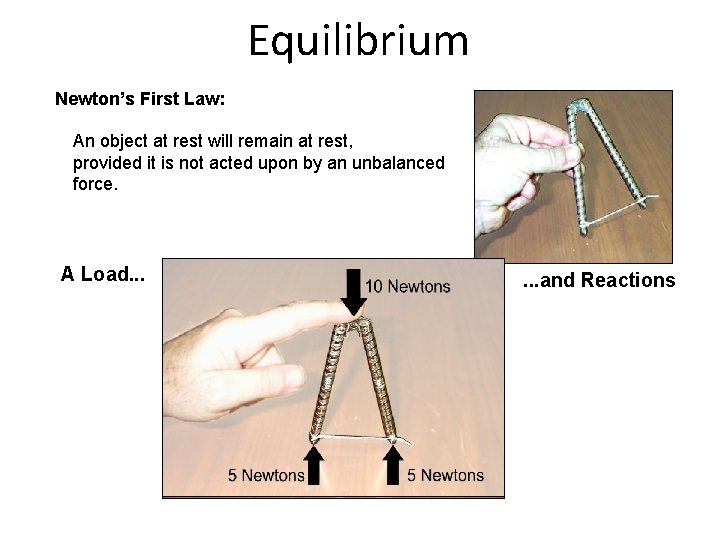
Equilibrium Newton’s First Law: An object at rest will remain at rest, provided it is not acted upon by an unbalanced force. A Load. . . and Reactions

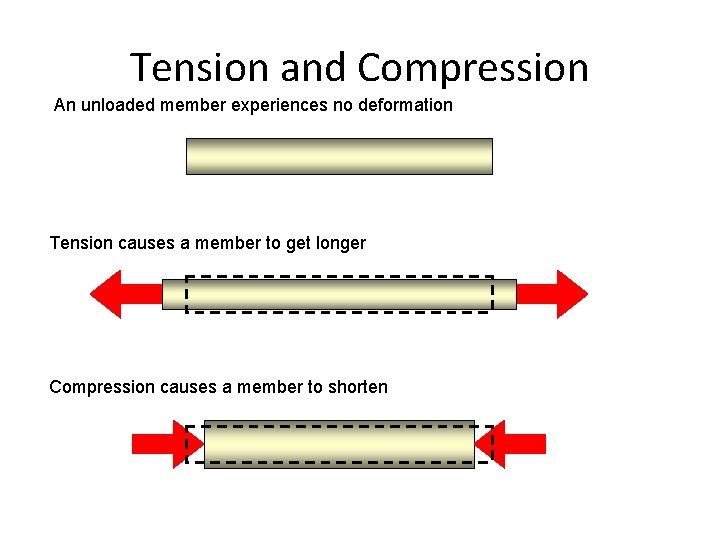
Tension and Compression An unloaded member experiences no deformation Tension causes a member to get longer Compression causes a member to shorten

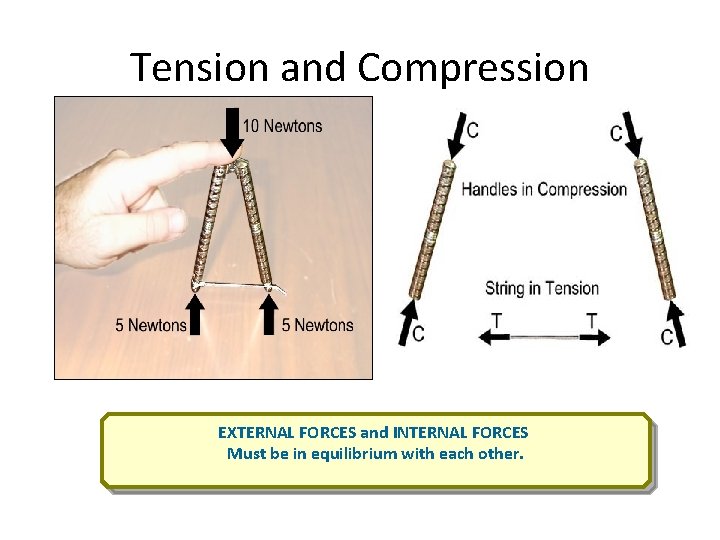
Tension and Compression EXTERNAL FORCES and INTERNAL FORCES Must be in equilibrium with each other.

Structural Analysis • For a given load, find the internal forces (tension and compression) in all members. • Why? • Procedure: – Model the structure: • Define supports • Define loads • Draw a free body diagram. – Calculate reactions. – Calculate internal forces using “Method of Joints. ”

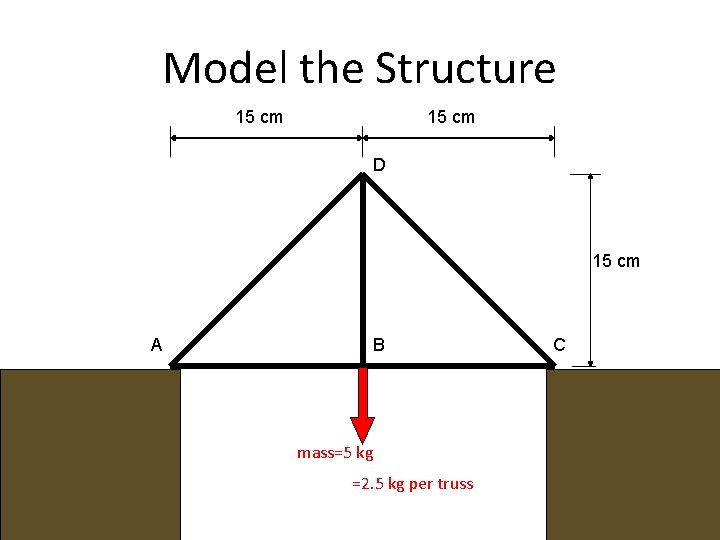
Model the Structure 15 cm D 15 cm A B mass=5 kg =2. 5 kg per truss C

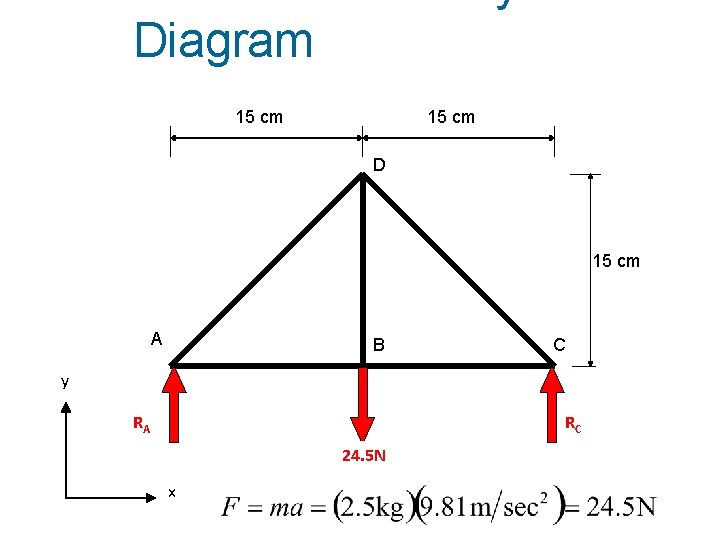
Diagram 15 cm D 15 cm A B C y RA RC mass=2. 5 kg 24. 5 N x

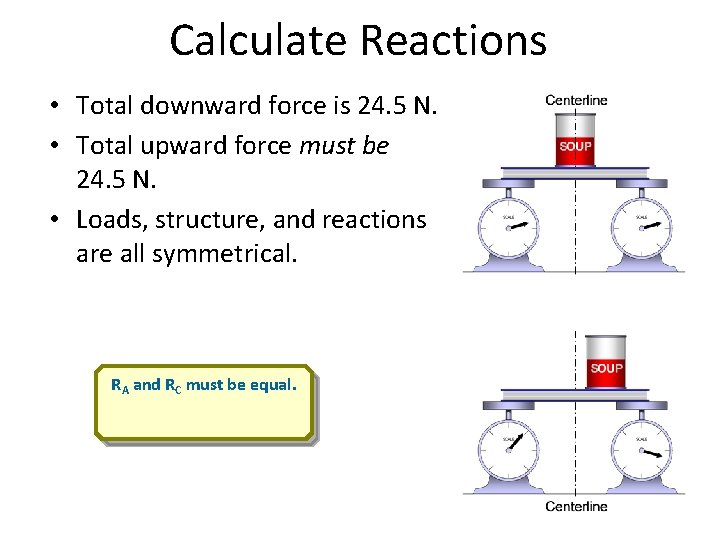
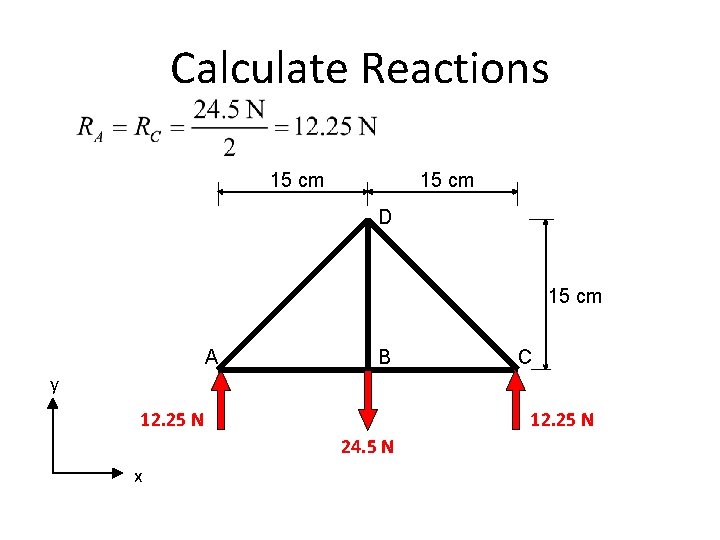
Calculate Reactions • Total downward force is 24. 5 N. • Total upward force must be 24. 5 N. • Loads, structure, and reactions are all symmetrical. RA and RC must be equal.

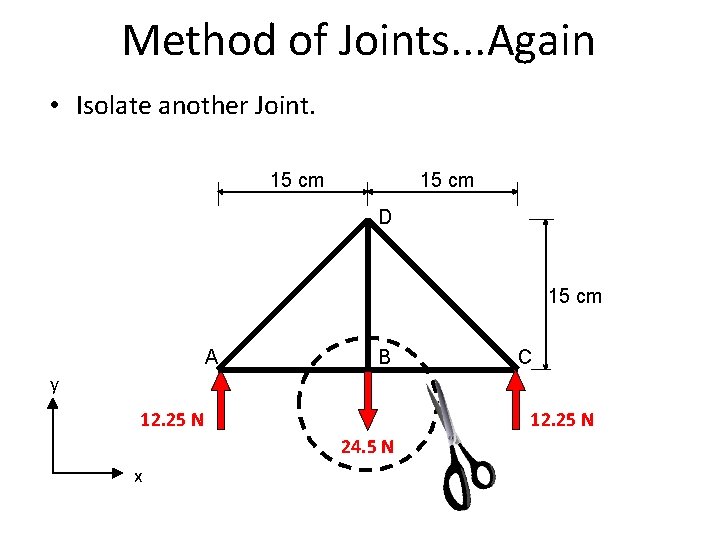
Calculate Reactions 15 cm D 15 cm A B C y 12. 25 RN A x 24. 5 N N R 12. 25 C

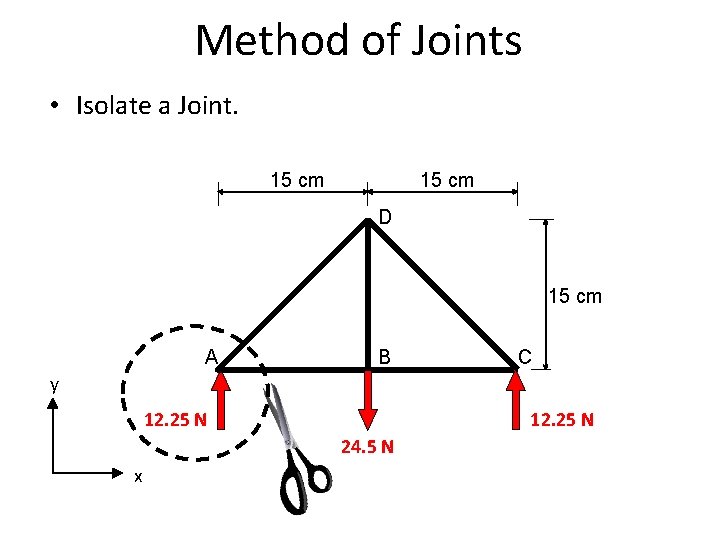
Method of Joints • Isolate a Joint. 15 cm D 15 cm A B C y 12. 3 NN 12. 25 24. 5 N x N R 12. 25 C

Method of Joints o Isolate a Joint. o Draw a free body diagram of the joint. n n n Include any external loads of reactions applied at the joint. Include unknown internal forces at every point where a member was cut. Assume unknown forces in tension. FAD A y FAB 12. 25 N x o Solve the Equations of Equilibrium for the Joint. EXTERNAL FORCES and INTERNAL FORCES Must be in equilibrium with each other.

Equations of Equilibrium • The sum of all forces acting in the x-direction must equal zero. FAD A y FAB 12. 25 N • The sum of all forces acting in the y-direction must equal zero. x • For forces that act in a diagonal direction, we must consider both the x-component and the ycomponent of the force.

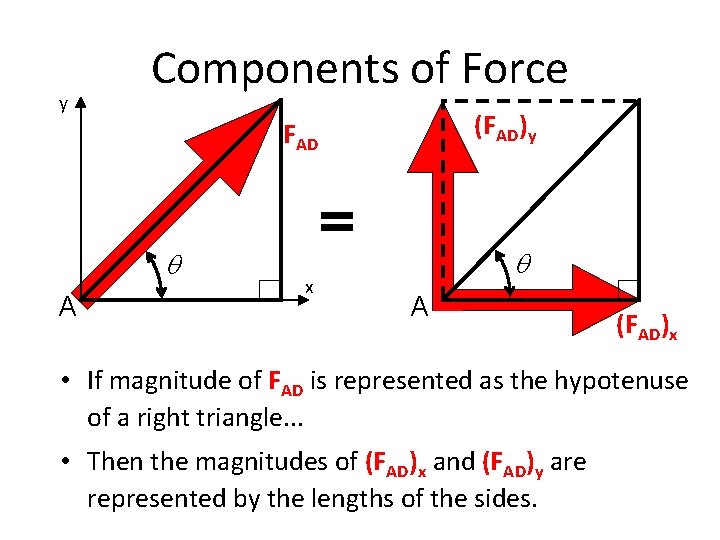
y Components of Force (FAD)y FAD q A x q A (FAD)x • If magnitude of FAD is represented as the hypotenuse of a right triangle. . . • Then the magnitudes of (FAD)x and (FAD)y are represented by the lengths of the sides.

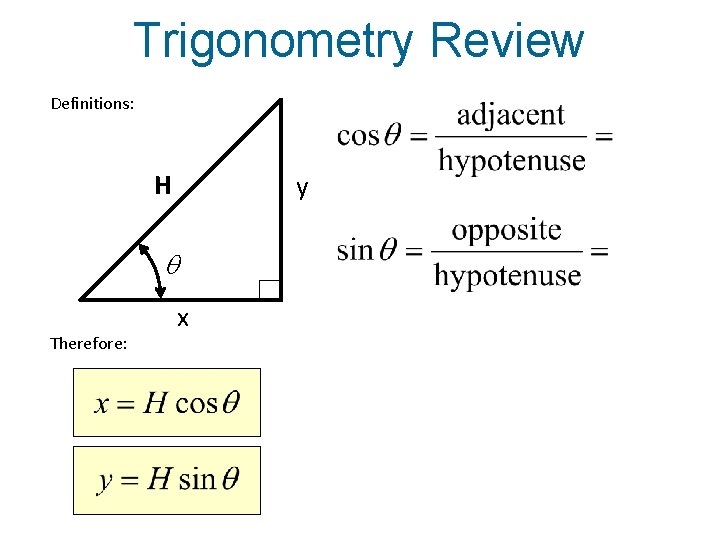
Trigonometry Review Definitions: H y q Therefore: x

Components of Force y (FAD)y FAD 45 o? q= A Therefore: x 45 o? q= A (FAD)x

Equations of Equilibrium 0. 707 FAD A y FAB 12. 3 N ? FAD 0. 707 FAD x FAB=12. 25 N (tension) FAD=17. 3 N (compression)

Method of Joints. . . Again • Isolate another Joint. 15 cm D 15 cm A B C y 12. 25 N 24. 5 N x N R 12. 25 C

Equations of Equilibrium FBD FAB FBC=12. 25 N (tension) B y 24. 5 N x FBD=24. 5 N (tension) FBC

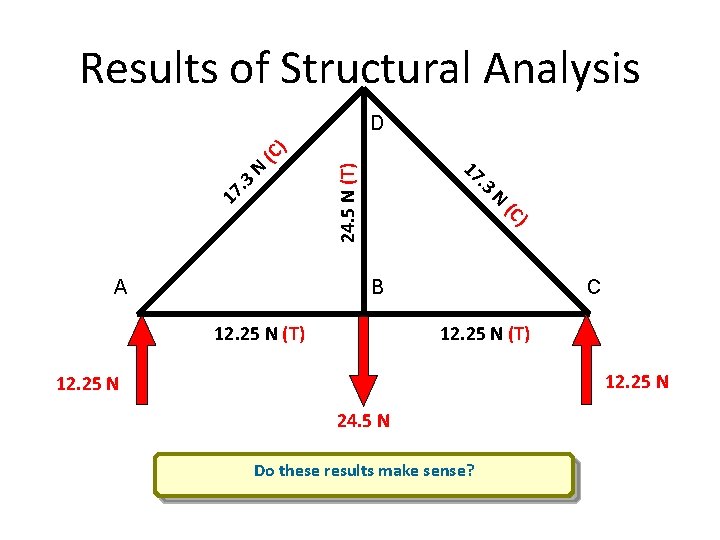
Results of Structural Analysis. 3 24. 5 N (T) N 17 . 3 ) (C A 17 N (C ) D B 12. 25 N (T) C 12. 25 N (T) 12. 25 N 24. 5 N Do these results make sense?

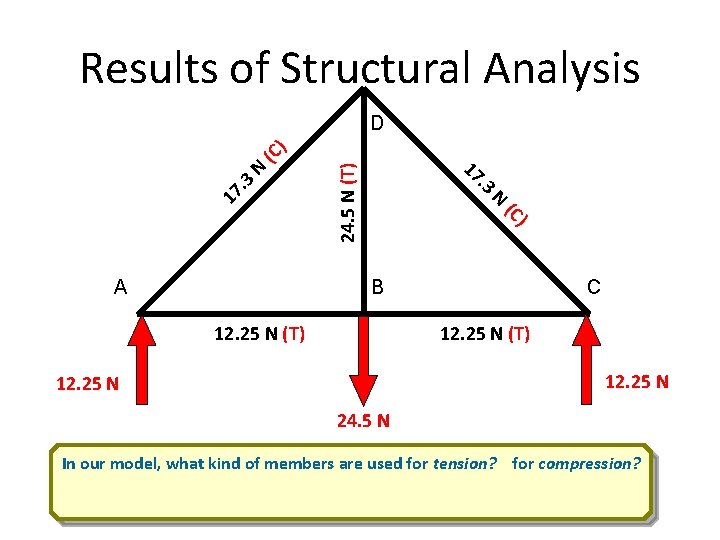
Results of Structural Analysis. 3 24. 5 N (T) N 17 . 3 ) (C A 17 N (C ) D B 12. 25 N (T) C 12. 25 N (T) 12. 25 N 24. 5 N In our model, what kind of members are used for tension? for compression?