What is a right triangle hypotenuse leg right

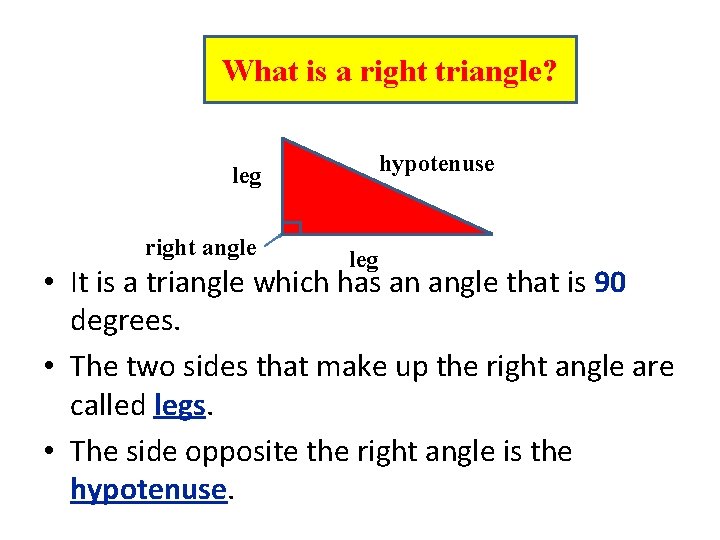
What is a right triangle? hypotenuse leg right angle leg • It is a triangle which has an angle that is 90 degrees. • The two sides that make up the right angle are called legs. • The side opposite the right angle is the hypotenuse.

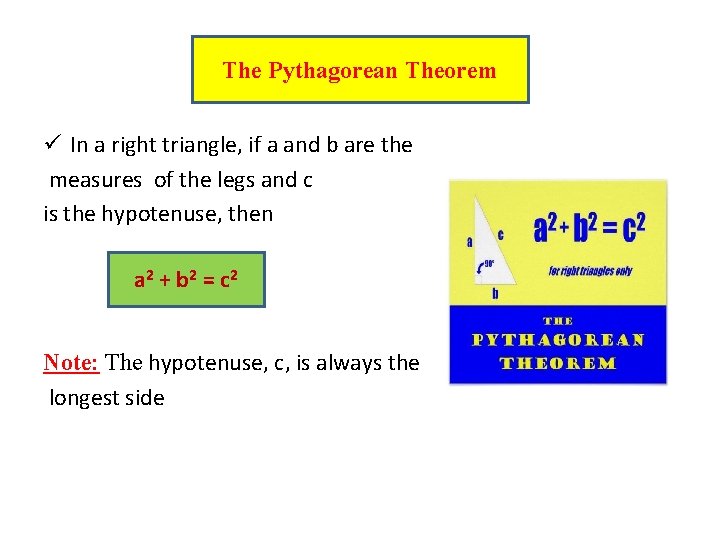
The Pythagorean Theorem ü In a right triangle, if a and b are the measures of the legs and c is the hypotenuse, then a 2 + b 2 = c 2 Note: The hypotenuse, c, is always the longest side

Proof of the Pythagorean Theorem Area of Whole Square: • It is a big square, with each side having a length of a+b, so the total area is: Area = side 2 = (a+b)2 • Area of the Pieces Now let's add up the areas of all the smaller pieces: First, the smaller (tilted) square has an area of Area = c 2 And there are four triangles; each one has an area of 1/2 ab So all four of them combined is A = 4(½ab) = 2 ab So, adding up the tilted square and the 4 triangles gives: A = c 2+2 ab

Both Areas Must Be Equal The area of the large square is equal to the area of the tilted square and the 4 triangles. This can be written as: (a+b) 2 = c 2 + 2 ab • Now, let us rearrange this to see if we can get the Pythagoras theorem: Start with: (a+b) 2 = c 2 + 2 ab Expand (a+b) 2 a 2+b 2+2 ab = c 2 + 2 ab Subtract "2 ab" from both sides: a 2+ b 2 = c 2 a 2 + b 2 = c 2 Pythagorean Theorem

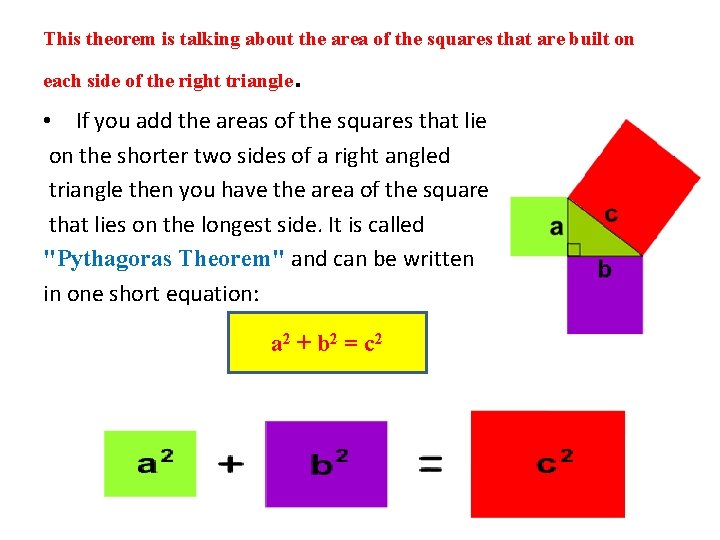
This theorem is talking about the area of the squares that are built on each side of the right triangle . • If you add the areas of the squares that lie on the shorter two sides of a right angled triangle then you have the area of the square that lies on the longest side. It is called "Pythagoras Theorem" and can be written in one short equation: a 2 + b 2 = c 2

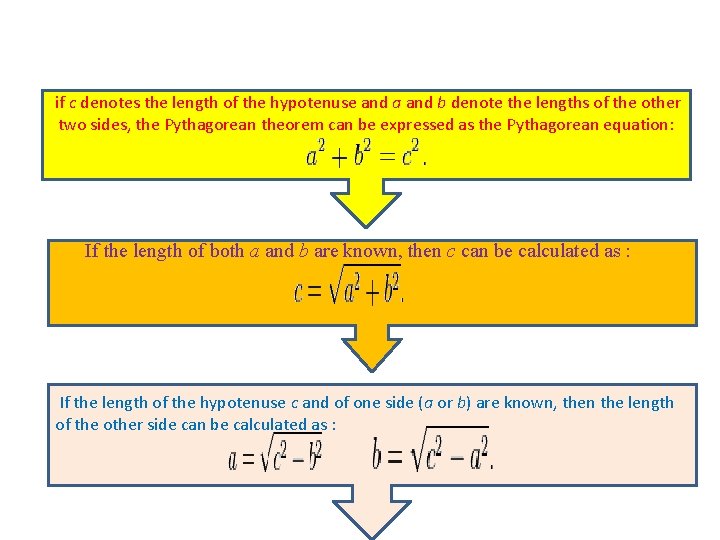
if c denotes the length of the hypotenuse and a and b denote the lengths of the other two sides, the Pythagorean theorem can be expressed as the Pythagorean equation: If the length of both a and b are known, then c can be calculated as : If the length of the hypotenuse c and of one side (a or b) are known, then the length of the other side can be calculated as :

Pythagorean Theorem Example: • If a right triangle has sides a = 3 and b = 4 and hypotenuse c = 5 a=3 then a 2 + b 2 = c 2 32 + 42 = 52 9 + 16 = 25 25 = 25 c=5 b=4

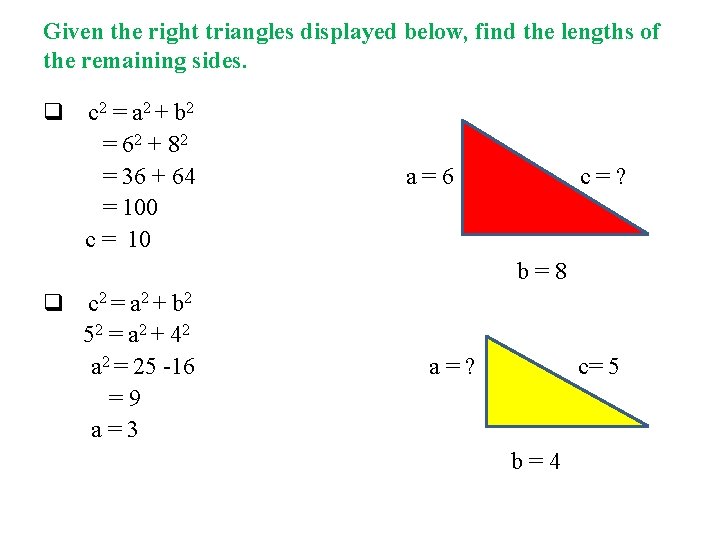
Given the right triangles displayed below, find the lengths of the remaining sides. q c 2 = a 2 + b 2 = 62 + 82 = 36 + 64 = 100 c = 10 a=6 c=? b=8 q c 2 = a 2 + b 2 52 = a 2 + 42 a 2 = 25 -16 =9 a=3 a=? c= 5 b=4

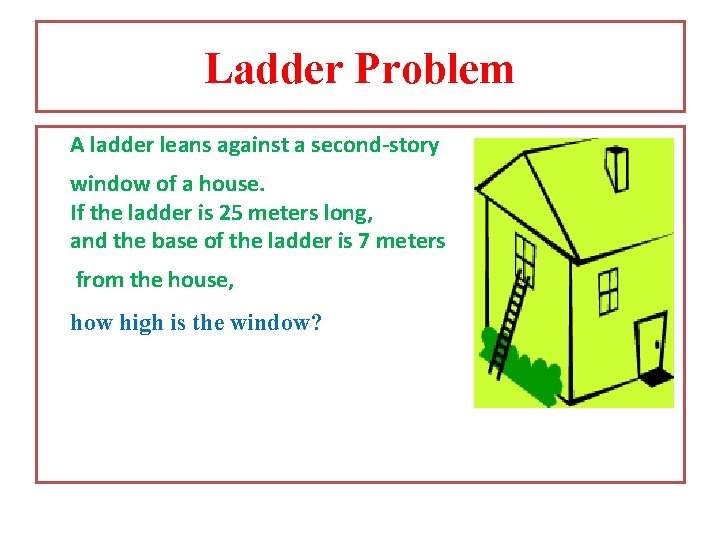
Ladder Problem A ladder leans against a second-story window of a house. If the ladder is 25 meters long, and the base of the ladder is 7 meters from the house, how high is the window?

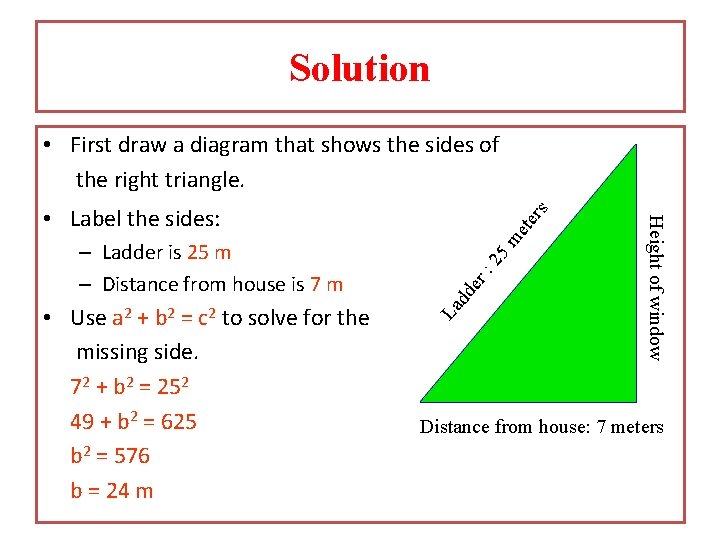
Solution • First draw a diagram that shows the sides of the right triangle. ete rs m 25 r: dd e • Use a 2 + b 2 = c 2 to solve for the missing side. 72 + b 2 = 252 49 + b 2 = 625 b 2 = 576 b = 24 m La – Ladder is 25 m – Distance from house is 7 m Height of window • Label the sides: Distance from house: 7 meters