What is a Polygon Section 3 4 A

A polygon is… • Closed figure with at least three segment sides • Sides

Naming a polygon… • Polygons are named with all endpoints in clockwise or counterclockwise

Vertices: A, B, C, D, E, and F Sides: ED, DC, CB, BA, AF,

Convex Polygon u No diagonal with points outside the polygon.

Concave or Non-convex Polygon u At least one diagonal with points outside the polygon.

Equilateral Polygon u All sides congruent

Equiangular Polygon u All angles congruent

Regular Polygon u Both equilateral and equiangular

Not Regular (Irregular) Polygon u Not equilateral nor equiangular

Number of Sides Polygon Name 4 Quadrilateral Number of Triangles Formed 2 Sum of

Number of Sides 5 Polygon Name Pentagon Number of Triangles Formed 3 Sum of

Number of Sides 6 Polygon Name Hexagon Number of Triangles Formed 4 Sum of

Names for other polygons have been proposed. Sides Name 9 Nonagon, Enneagon 11 Undecagon,

To find the interior angle sum for a regular polygon: (n – 2) 180

To find the measure of one interior angle in a regular polygon: Sum of

The sum of the measures of the exterior angles of a polygon = o

To find the measure of one exterior angle in a regular polygon: Sum of

Slides: 24

Download presentation

What is a Polygon? Section 3. 4

A polygon is… • Closed figure with at least three segment sides • Sides must intersect only at endpoints

Polygons Not Polygons

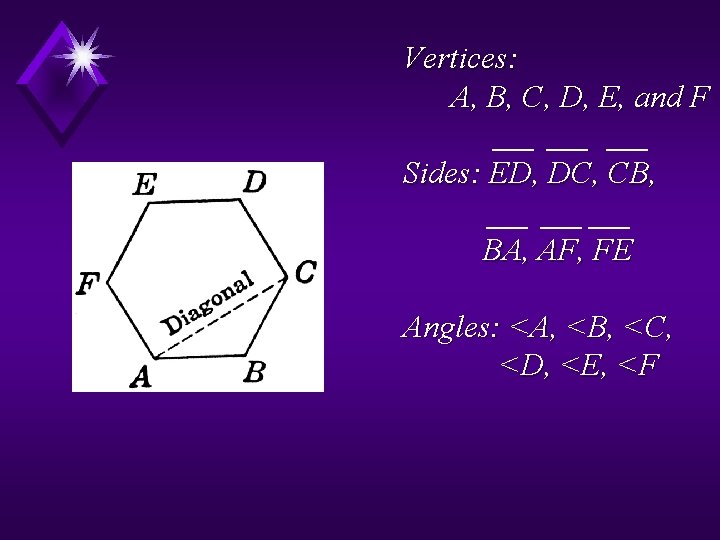
Naming a polygon… • Polygons are named with all endpoints in clockwise or counterclockwise order • Polygon ABCDEF • Polygon EDCBAF

Vertices: A, B, C, D, E, and F Sides: ED, DC, CB, BA, AF, FE Angles: <A, <B, <C, <D, <E, <F

Convex Polygon u No diagonal with points outside the polygon.

Concave or Non-convex Polygon u At least one diagonal with points outside the polygon.

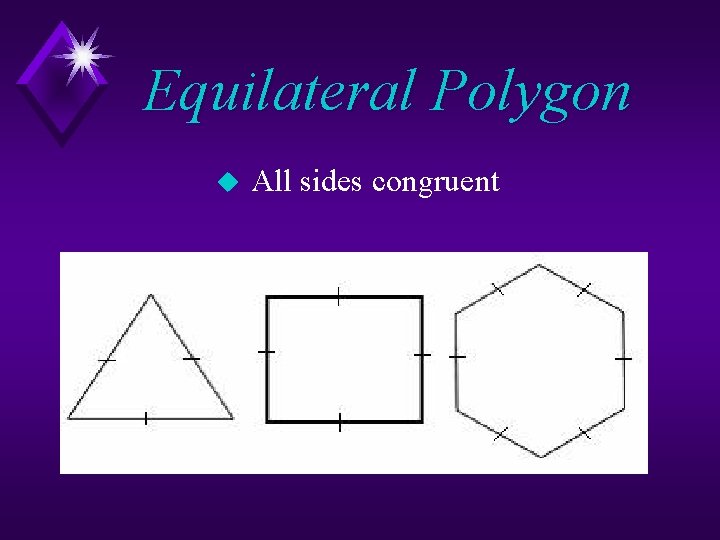
Equilateral Polygon u All sides congruent

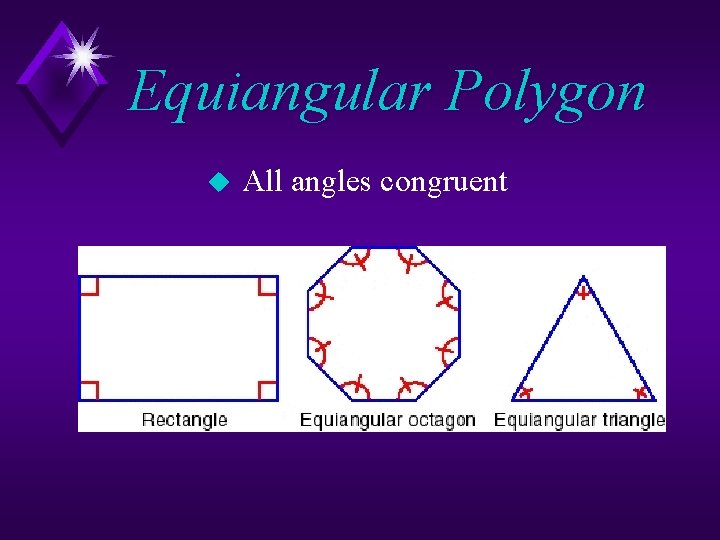
Equiangular Polygon u All angles congruent

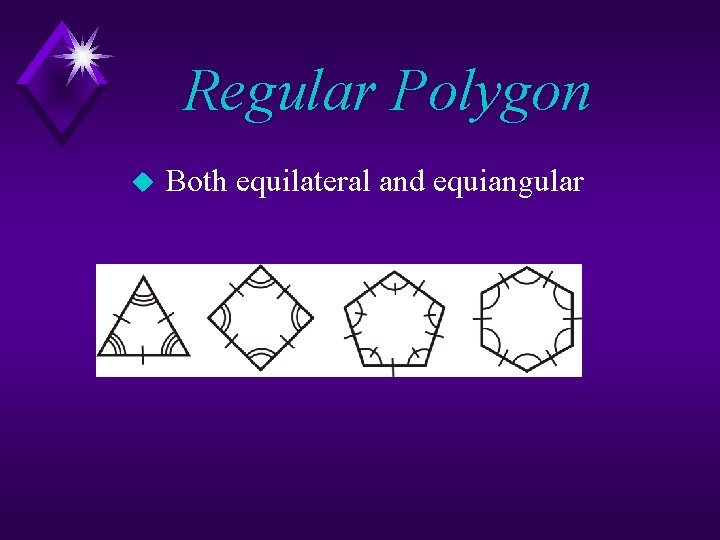
Regular Polygon u Both equilateral and equiangular

Not Regular (Irregular) Polygon u Not equilateral nor equiangular

Summary

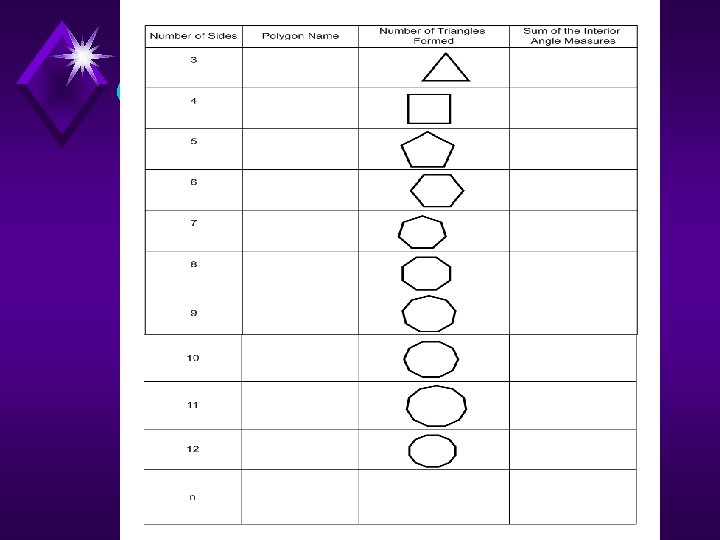
Complete the Chart

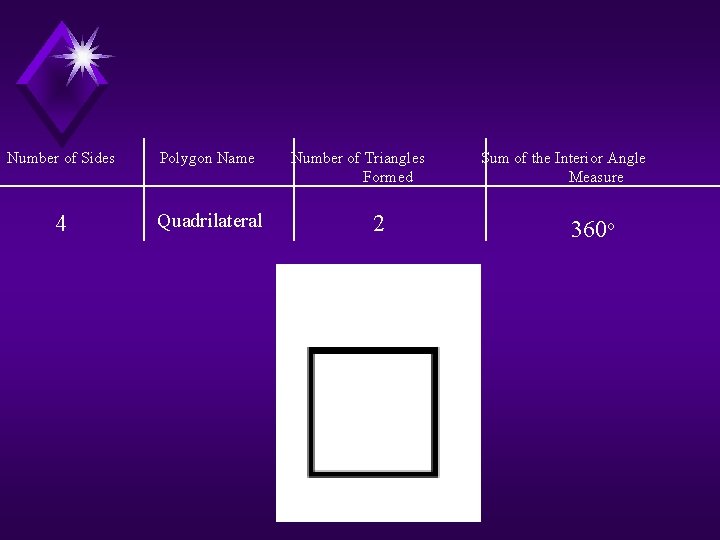
Number of Sides Polygon Name 4 Quadrilateral Number of Triangles Formed 2 Sum of the Interior Angle Measure 360 o

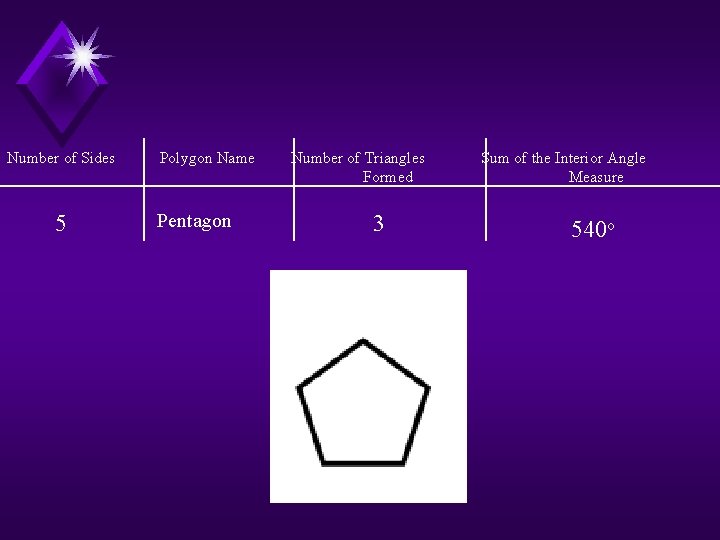
Number of Sides 5 Polygon Name Pentagon Number of Triangles Formed 3 Sum of the Interior Angle Measure 540 o

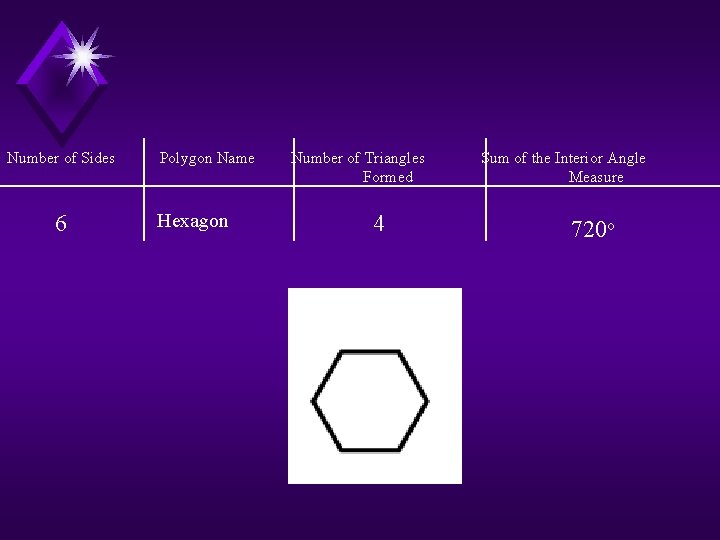
Number of Sides 6 Polygon Name Hexagon Number of Triangles Formed 4 Sum of the Interior Angle Measure 720 o

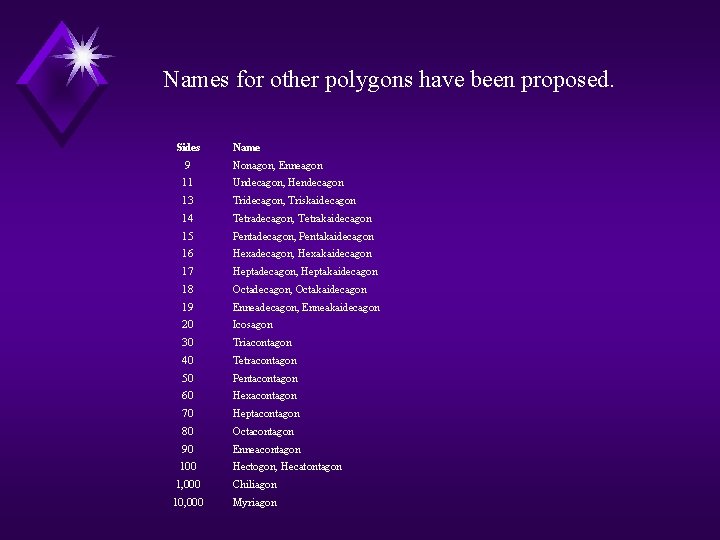
Names for other polygons have been proposed. Sides Name 9 Nonagon, Enneagon 11 Undecagon, Hendecagon 13 Tridecagon, Triskaidecagon 14 Tetradecagon, Tetrakaidecagon 15 Pentadecagon, Pentakaidecagon 16 Hexadecagon, Hexakaidecagon 17 Heptadecagon, Heptakaidecagon 18 Octadecagon, Octakaidecagon 19 Enneadecagon, Enneakaidecagon 20 Icosagon 30 Triacontagon 40 Tetracontagon 50 Pentacontagon 60 Hexacontagon 70 Heptacontagon 80 Octacontagon 90 Enneacontagon 100 Hectogon, Hecatontagon 1, 000 Chiliagon 10, 000 Myriagon

You Finish the Chart. . .

To find the interior angle sum for a regular polygon: (n – 2) 180 o where n is the number of sides

To find the measure of one interior angle in a regular polygon: Sum of interior angles Number of sides OR (n – 2) 180 o Number of sides

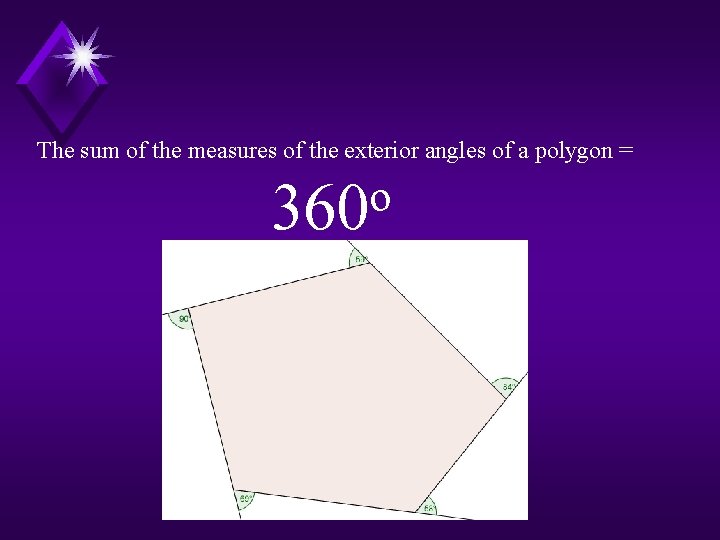
The sum of the measures of the exterior angles of a polygon = o 360

To find the measure of one exterior angle in a regular polygon: Sum of exterior angles Number of angles = 360 o n