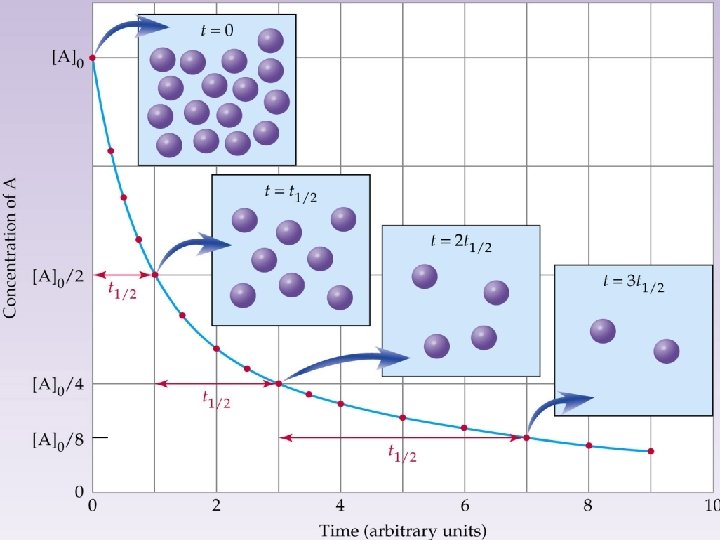
What does rate of reaction mean The speed

What does rate of reaction mean? The speed of different chemical reactions varies hugely. Some reactions are very fast and others are very slow. The speed of a reaction is called the rate of the reaction. What is the rate of these reactions? rusting baking explosion slow fast very fast

REACTION RATES • A reaction rate –measures how quickly the reactant is consumed as it coverts into product – Rates measure the speed of any change that occurs within an interval of time – The interval of time may range from fractions of a second to centuries • Rates of chemical change usually are expressed as the change in concentration of reactant over time.

CALCULATE THE AVG. RATE OF RXN

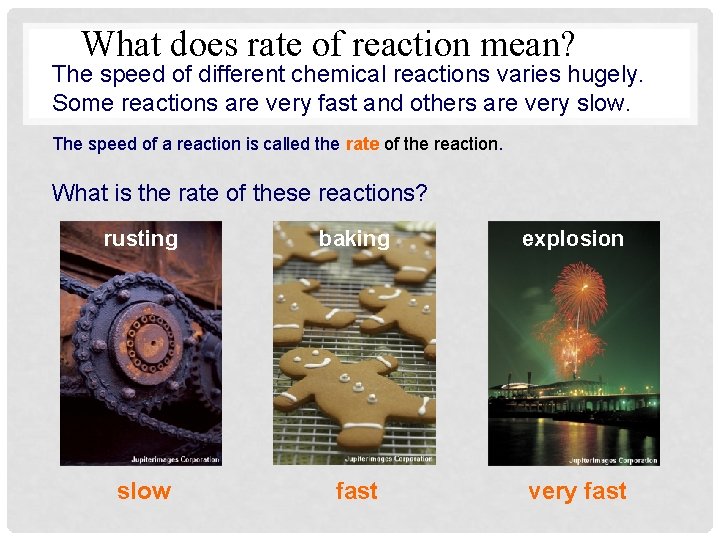
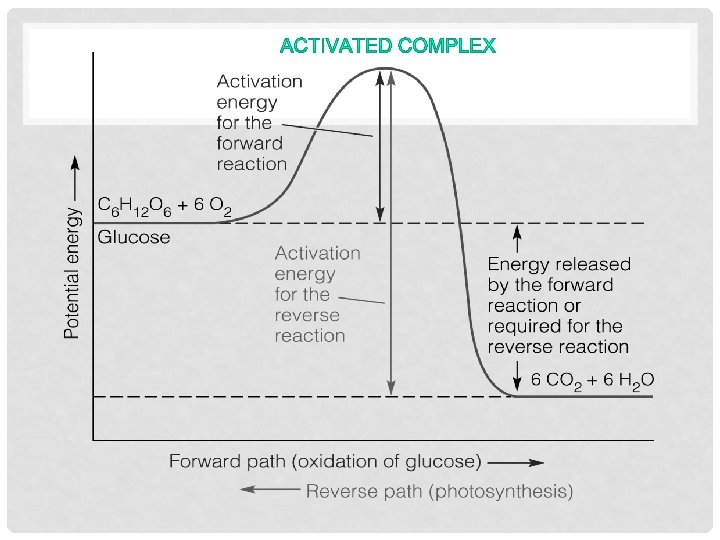
COLLISION THEORY 1. Reacting substances must collide 2. Reacting substances must collide with the correct orientations. 3. Reacting substances must collide with sufficient energy to form the activated complex

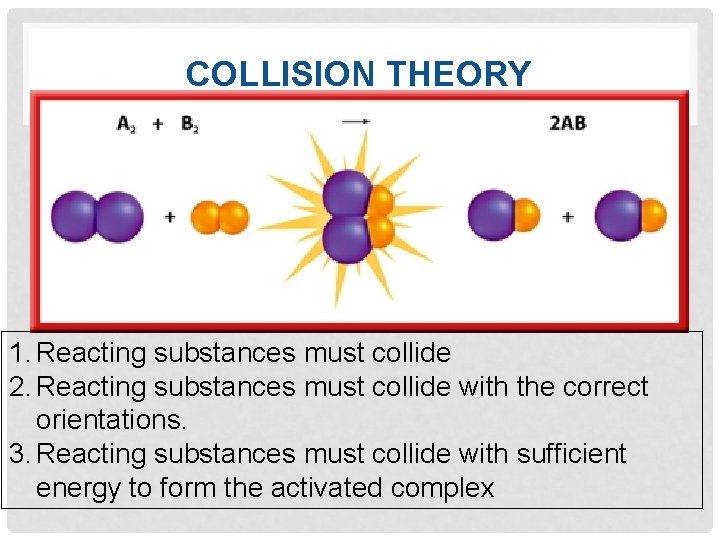
ENERGY FLOW Endothermic Rxn’s-the reactants have less potential energy than the products. Energy must be input in order to raise the particles up to the higher energy level. Energy + A + B --> AB Exothermic Rxn’s-the reactants have more potential energy than the products. The extra energy is released to the surroundings. A + B --> AB + Energy

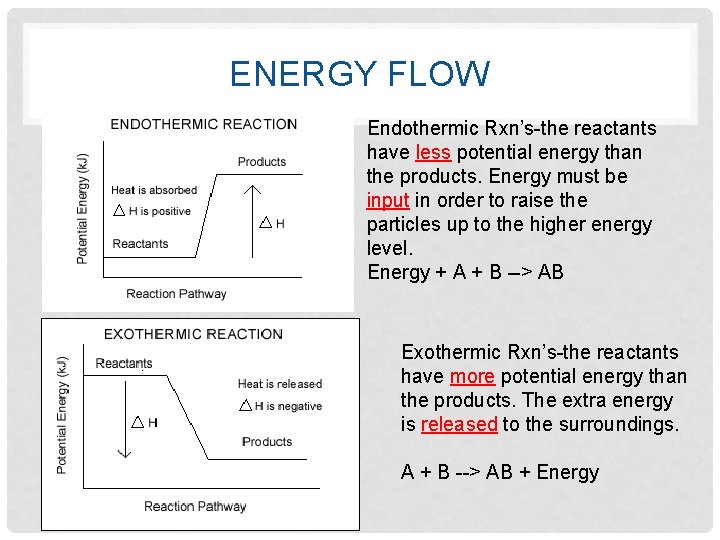
ACTIVATION COMPLEX • Activated complex-temporary, unstable arrangement of atoms that may form products or may break apart back to reactants. The ‘A. C. ’ can form both reactants and products Therefore it is referred to as the ‘transition state’

REACTIONS The minimum amount of energy needed for the particles to react is called the activation energy, and is different for each reaction. The rate of a reaction depends on two things: l the frequency of collisions between particles l the energy with which particles collide.

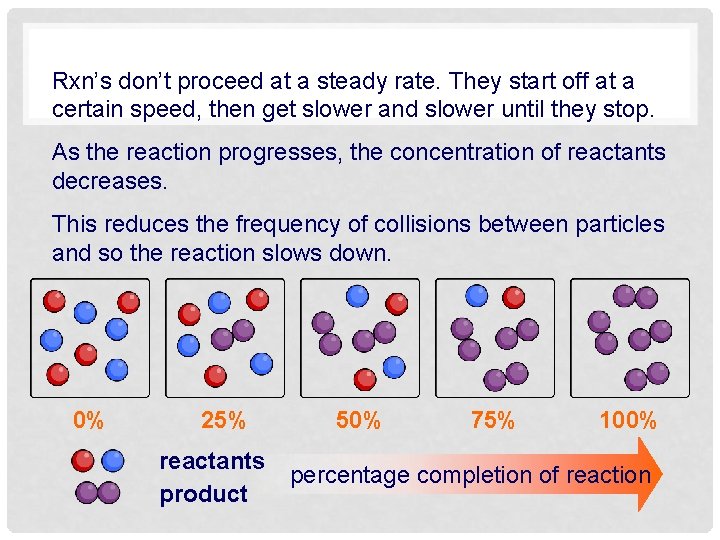
Rxn’s don’t proceed at a steady rate. They start off at a certain speed, then get slower and slower until they stop. As the reaction progresses, the concentration of reactants decreases. This reduces the frequency of collisions between particles and so the reaction slows down. 0% 25% reactants product 50% 75% 100% percentage completion of reaction

REACTANT–PRODUCT MIX

COLLISIONS AND REACTIONS: SUMMARY

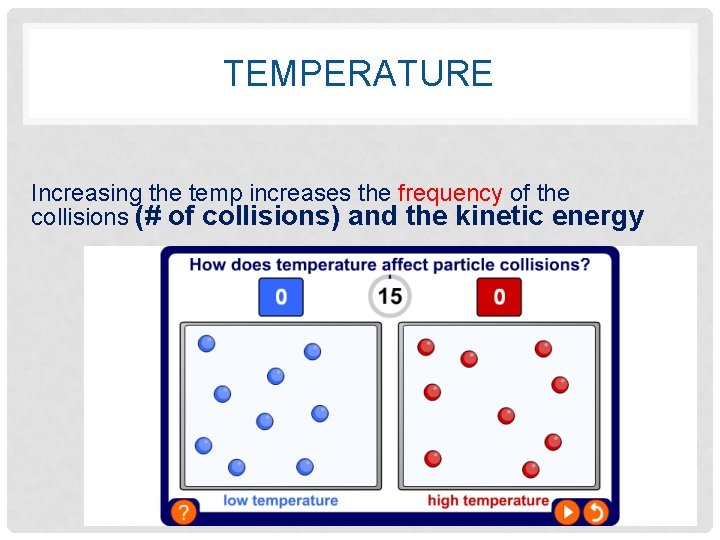
Changing the rate of reactions Anything that increases the number of successful collisions between reactant particles will speed up a reaction. What factors affect the rate of reactions? l Increased temperature l Increased concentration of dissolved reactants, and increased pressure of gaseous reactants l Increased surface area of solid reactants l Use of a catalyst.

TEMPERATURE Increasing the temp increases the frequency of the collisions (# of collisions) and the kinetic energy

CONCENTRATION • The more reacting particles you have in a given volume, the higher the rate of rxn. • Cramming more particles into a fixed volume increases the concentration of reactants,

SURFACE AREA • The smaller the particle size, the larger the surface area for a given mass of particles • The total surface area of a solid or liquid reactant has an important effect on the rate of reaction. • An increase in surface area increases the amount of the reactant exposed for collision to take place… – Which increases the collision frequency and the reaction rate.

SURFACE AREA o Increase surface area of solid-dissolve it. o Grinding solids into a fine powder also increases the surface area of reactants

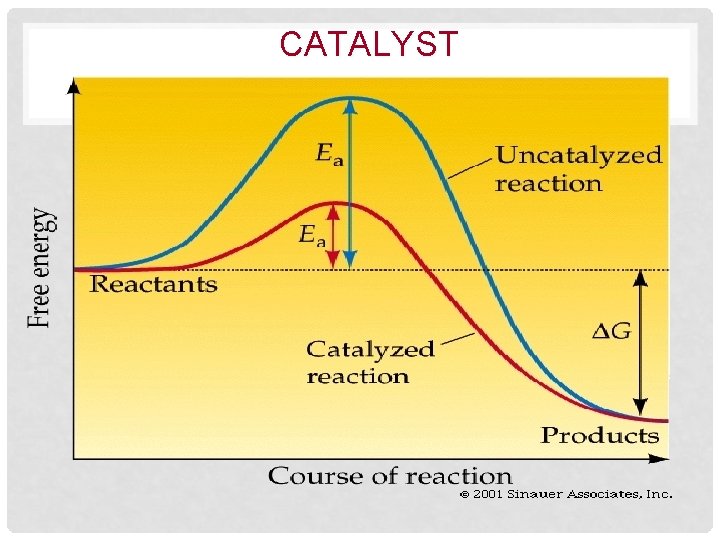
CATALYST o A catalyst is a substance that increases the rate of a rxn without being changed during the rxn • o They permit rxns to proceed at lower energy than is normally required With a lower activation energy more reactants can form products in a given amount of time.

CATALYST

CATALYST o o Heterogeneous Catalysts- exists in a physical state different than that of the rxn it catalyzes Homogeneous Catalysts-exists in the same physical state as the rxn it catalyzes

• End for regular chem

RATE LAWS • Begin for honors chem

Rate Laws • The rate of a rxn depends in part on the concentration of the reactants – Concentration is a measure of how much stuff is available to react • For a rxn in which reactant A reacts to form product B in 1 step, you can write a simple rxn eqn: A B • The speed that A forms B is dependent on how the conc of A changes over time – As the conc of A decreases the rate of the rxn generally decreases

Rate Laws • You can express the rate as the disappearance of A (DA) with respect to the change in time (Dt) • The rate of disappearance of A is therefore, proportional to the concentration or molarity (# of moles/Liter) of reactant A • This proportionality can be expressed as a constant (k) multiplied by the concentration of reactant A • n is a category that the rxn fits in called an order n k[A]

Rate Laws • This mathematical expression is called a differential rate law or just, rate law – A rate law is an expression which relates the rate of a rxn to the conc of reactants • The magnitude of the rate constant (k) depends on the conditions at which the rxn is conducted – *If reactant A reacts to form product B quickly, the value of k will be large – *If reactant A reacts to form B slowly, the value of k will be small

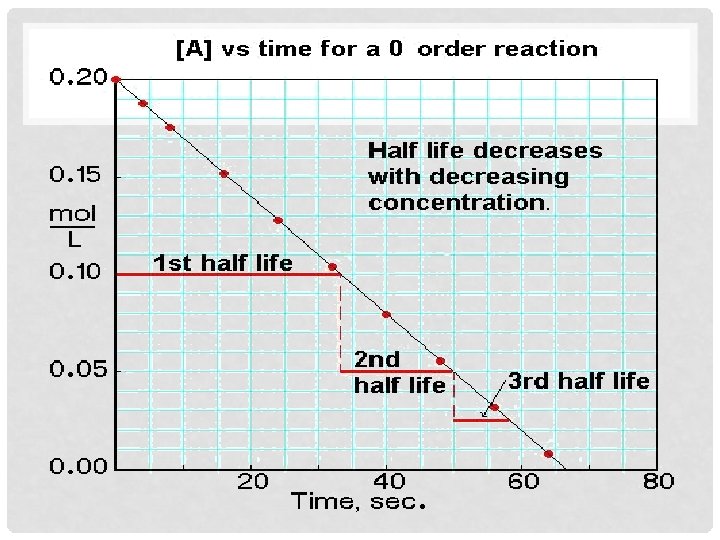
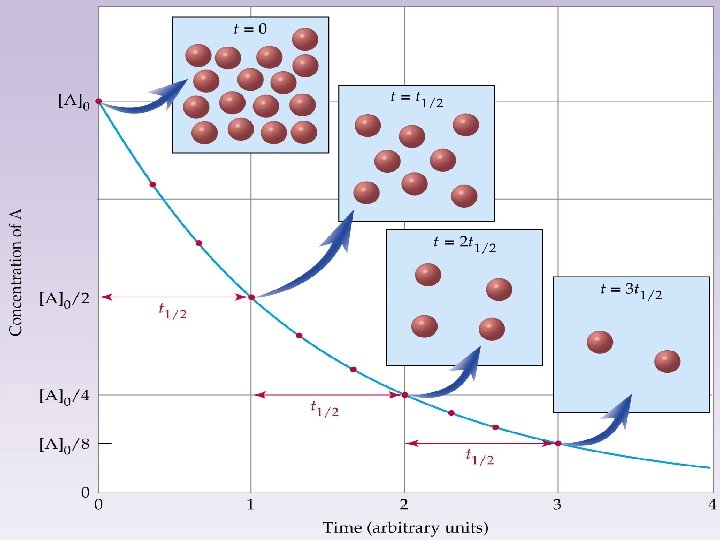
Rate Laws • Rxns are classified as either zero-order, first-order, second-order, or mixed order (higher order) rxns. – The rate of chemical rxns and the size of the rate constant (k) is dependent on the “order” of the rxn • Zero-Order Rxns – (m = 0) have a constant rate. This rate is independent of the conc of the reactants. The rate law is: k, with k having the units of M/sec. – The half-life of a zero-order reaction steadily decreases

Rate Laws • First-Order Reactions – (m = 1) has a rate proportional to the conc of one of the reactants. – A common example of a first-order rxn is the phenomenon of radioactive decay. The rate law is: k[A]1 (or B instead of A), with k having the units of sec-1. – The half life is a constant.

Rate Laws • Second-Order Reactions – (order = 2) has a rate proportional to the conc of the square of a single reactant or the product of the conc of two reactants that are first-order each. – Rate law =k[A]2 (or substitute B for A or k multiplied by the concentration of A, [A], times the concentration of B, [B]), with the units of the rate constant M-1 sec-1 – The half life steadily increases for second-order reactions

Determining Rate Laws • Rate laws can only be determined experimentally. – One way to experimentally determine the order and the rate constant is to determine a class of rate laws called Integrated Rate Laws. o Integrated Rate Laws are determined through graphical analysis. • Integrated rate laws can help us write the rate law for a reaction

Determining the Rate Law o We first gather data on how the [A] changes over time We then graph the data 3 different ways • And we look for a pattern with the data Integrated Rate Law: Zero Order • • The Zero order integrated rate law shows that its rate is independent of the [A] – Where graphing [A] vs. time is a straight line with a slope of -k

Zero Order Rate Law Integrated Rate Law k [A] = -kt + [A]0 Rate Constant Slope = - k

Integrated Rate Law: First Order • The first order integrated rate law can be used to determine [A] at any time. – Where graphing the ln[A] vs. time produces a straight line – If the graph is a straight line, then the rxn has first-order kinetics and it’s rate constant (k) = slope x (-1)

First Order Rate Law k[A] Integrated ln[A] = -kt + ln[A]0 Rate Law Rate Constant Slope = - k

Integrated Rate Law: Second Order • The second-order integrated rate law is be used to determine the [A] at any time. – If we achieve a straight line when the inverse of [A] is graphed vs. time – If 1/[A] vs time produces a linear function, the kinetics is 2 nd order and the rate constant is the slope of the line

Second Order Rate Law Integrated Rate Law k[A]2 Rate Constant Slope = k

Rate Law Zero-Order First-Order Second-Order k k[A]2 Integrated Rate Law Units of constant Linear Plot Half-Life slope= -k slope= k

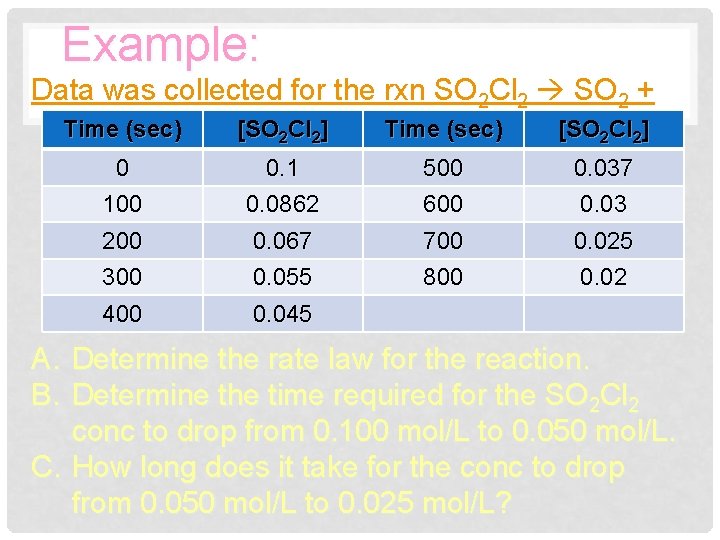
Example: Data was collected for the rxn SO 2 Cl 2 SO 2 + Cl Time [SO 2 Cl 2] Time (sec) [SO 2 Cl 2] 2: (sec) 0 100 0. 1 0. 0862 500 600 0. 037 0. 03 200 300 0. 067 0. 055 700 800 0. 025 0. 02 400 0. 045 A. Determine the rate law for the reaction. B. Determine the time required for the SO 2 Cl 2 conc to drop from 0. 100 mol/L to 0. 050 mol/L. C. How long does it take for the conc to drop from 0. 050 mol/L to 0. 025 mol/L?

[SO 2 Cl 2] vs. time Graph the data 3 different ways 0. 1 0. 09 0. 08 [SO 2 Cl 2] 0. 07 ln[SO 2 Cl 2] vs. time 0. 06 0. 05 -2 0. 04 0 100 -2. 8 700 -3 800 -2. 2 0. 03 300 400 500 600 700 800 900 -2. 4 0. 02 -2. 6 0 0 100 200 300 400 Time (sec) 500 600 1/[SO 2 Cl 2] vs. time ln[SO 2 Cl 2] 0. 01 -3. 2 -3. 4 60 -3. 6 -3. 8 50 -4 Time (sec) 40 1/[SO 2 Cl 2] 200 30 20 10 0 0 100 200 300 400 Time (sec) 500 600 700 800 Choose the one that makes a straight line

Example: The ln[SO 2 Cl 2] vs time produced a straight line when graphed. So the rxn is a first order rxn which fits the integrated law: ln[SO 2 Cl 2] = -kt + ln[SO 2 Cl 2]0 This indicates a 1 st order rxn, so our rate law is so far k[SO Cl ]1 2 2 k can be determined by negative of the slope, according to the regression line our rate law ends up as: 1 0. 002 L/mol • sec [SO 2 Cl 2] The ½ life equation that fits the integrated law for the first order rxn is… t =0. 693/k 1/2

Example: So the time it takes to go from 0. 1 mol/L to 0. 05 mol/L is calculated by… t 1/2 = 0. 693/0. 002 = 345. 6 sec To go from 0. 05 mol/L to 0. 025 mol/L it takes another 345. 6 sec, because the half-life of a 1 st order reaction is constant

Rate Laws • In some kinds of rxns, such as double replacement, 2 substances react to give products • The coefficients in the eqn for such a rxn can be represented by lower-case letters: a. A + b. B c. C + d. D • For a 1 step rxn of A+B, the rate of rxn is dependent on the concentrations of reactants A & B • It’s rate law would follow the eqn: Rate = k[A]a[B]b

Rate Laws o o o When each of the exponents a & b in the rate law equals 1, the rxn is said to be 1 st order in A, 1 st order in B, & 2 nd order overall The overall order of a rxn is the sum of the exponents for the individual reactants The rate law gives a chemist valuable information about the mechanism of a reaction • The mechanism of the rxn is the path a rxn might take to produce products

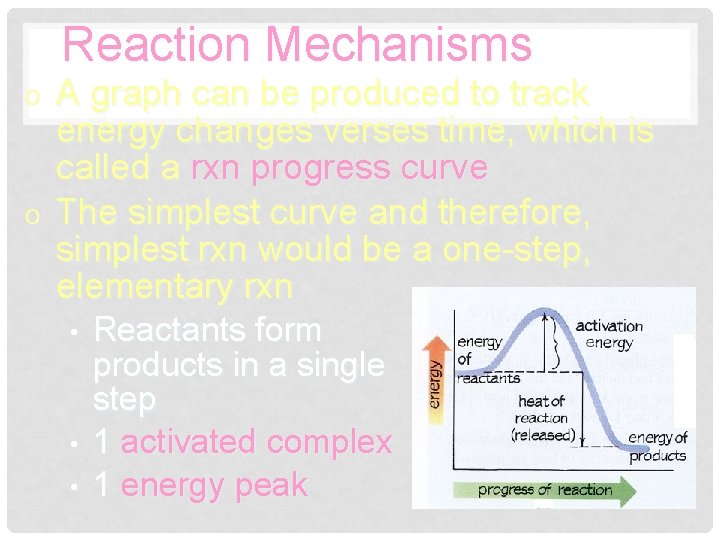
Reaction Mechanisms o o A graph can be produced to track energy changes verses time, which is called a rxn progress curve The simplest curve and therefore, simplest rxn would be a one-step, elementary rxn • • • Reactants form products in a single step 1 activated complex 1 energy peak

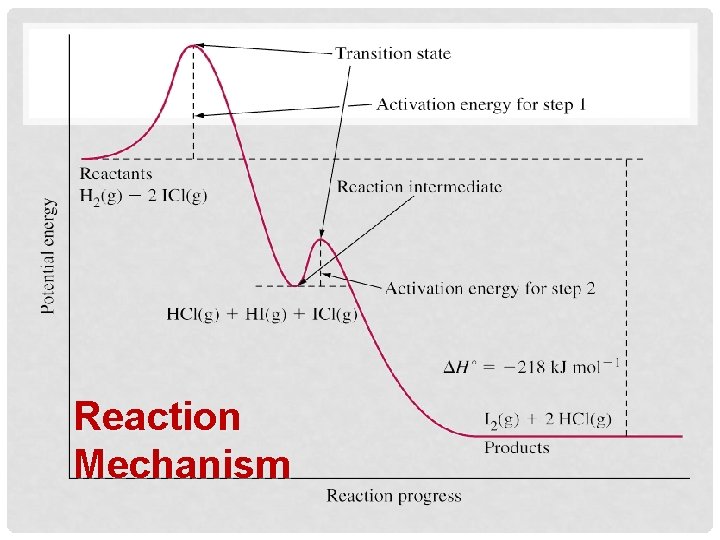
Reaction Mechanisms • For a more complex rxn, or a higher order rxn, the rxn progress curve resembles a series of hills & valleys – – The peaks correspond to the energies of the activated complexes Each valley represents an intermediate product which becomes a react of the next stage of the rxn • Intermediates have a significant lifetime compared with an activated complex – They have real ionic or molecular structures and some stability

Reaction Mechanism • Intermediate products do not appear in the overall eqn for a rxn • For example in the following overall rxn: H 2(g) + 2 ICl(g) <==> I 2(g) + 2 HCl(g) o This rxn is believed to be a 2 part rxn • There is an intermediate reaction in between the reactants and products. 1) H 2(g) + 2 ICl(g) + HI(g) 2) ICl(g) + HI(g) I 2(g) +2 HCl(g)

Reaction Mechanism

Reaction Mechanism o If a chem rxn proceeds in a sequence of steps, the rate law is determined by the slowest step because it has the lowest rate. • • The slowest step is called the ratedetermining step A mechanism can be proposed for any reaction, but the observed rate law (from experiments), must be the same as the derived rate law from a reaction mechanism

Reaction Mechanism o Consider this rxn: NO 2 + CO NO + CO 2 the rxn is believed to be a 2 step process following this mechanism Step 1: NO 2 + NO 2 NO + NOSLOW 3 • 2 2 3 Step 2: NO 3 + CO NO 2 + COFAST 2 o The 1 st step is the slower of the 2 steps and is therefore the rate-determining step Its rate law: R=k[NO 2]2