What Does a Single LightRay Reveal About a

What Does a Single Light-Ray Reveal About a Transparent Object? Chia-Yin Tsai Ashok Veeraraghavan Aswin C. Sankaranarayanan ICIP 2015

image courtesy: Huang, Juinn-Kai

Light ray correspondence ? Known entities are marked in green.

Light ray correspondence Known entities are marked in green.

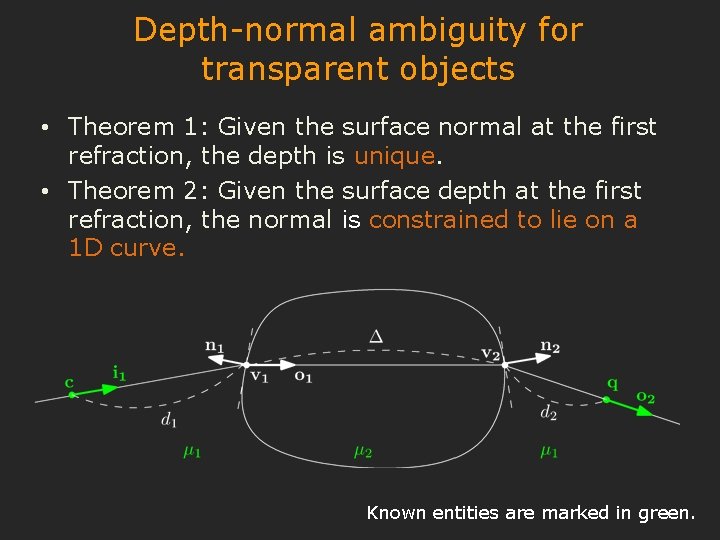
Depth-normal ambiguity for transparent objects • Theorem 1: Given the surface normal at the first refraction, the depth is unique. • Theorem 2: Given the surface depth at the first refraction, the normal is constrained to lie on a 1 D curve. Known entities are marked in green.

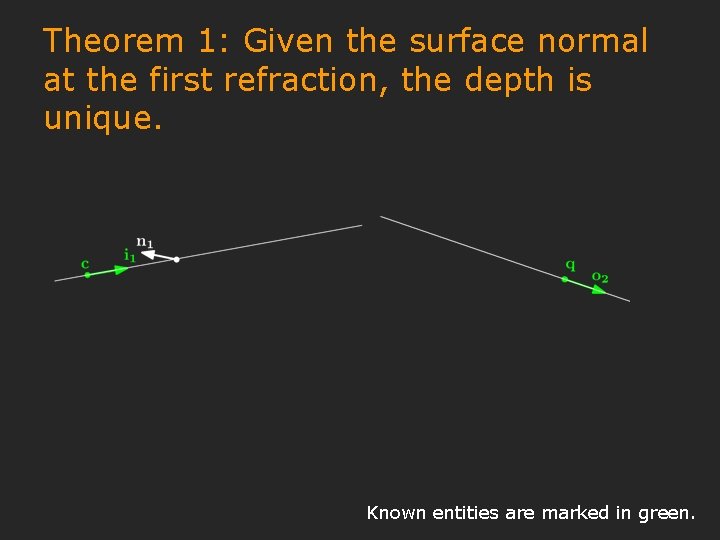
Theorem 1: Given the surface normal at the first refraction, the depth is unique. Known entities are marked in green.

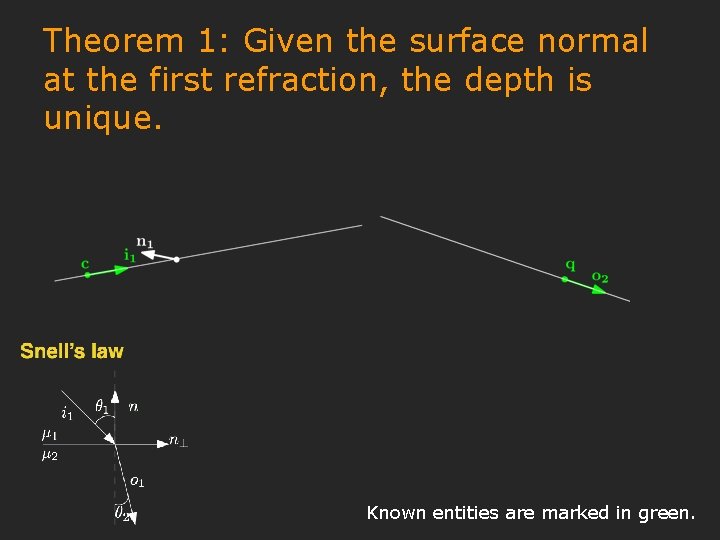
Theorem 1: Given the surface normal at the first refraction, the depth is unique. Known entities are marked in green.

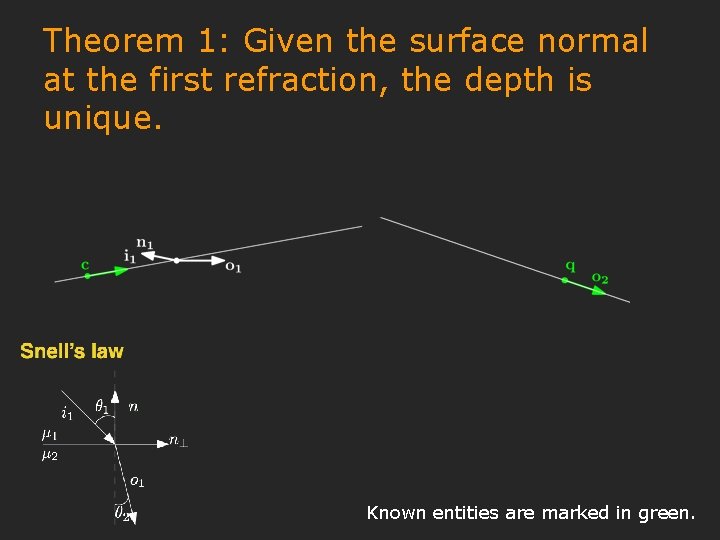
Theorem 1: Given the surface normal at the first refraction, the depth is unique. Known entities are marked in green.

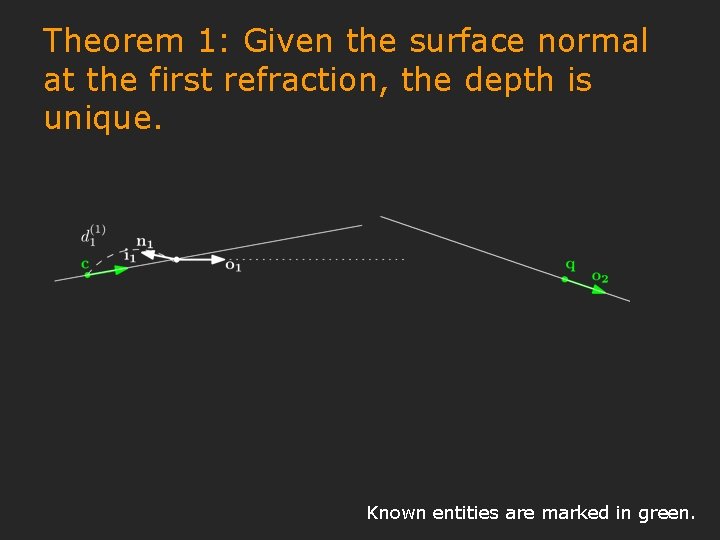
Theorem 1: Given the surface normal at the first refraction, the depth is unique. Known entities are marked in green.

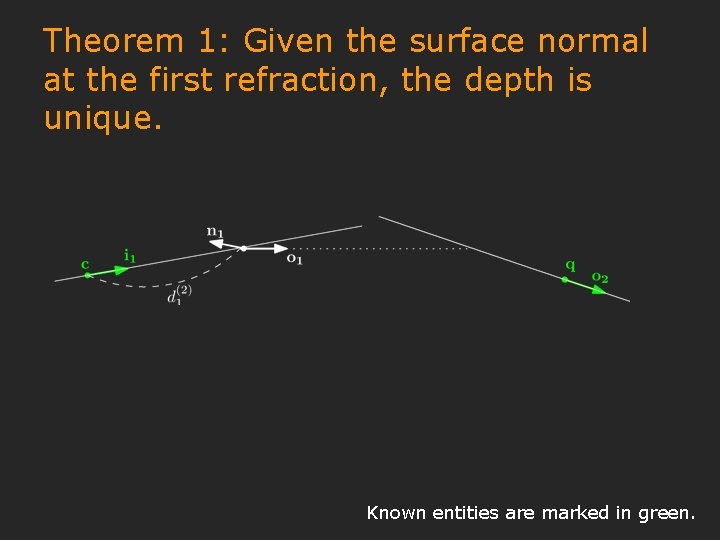
Theorem 1: Given the surface normal at the first refraction, the depth is unique. Known entities are marked in green.

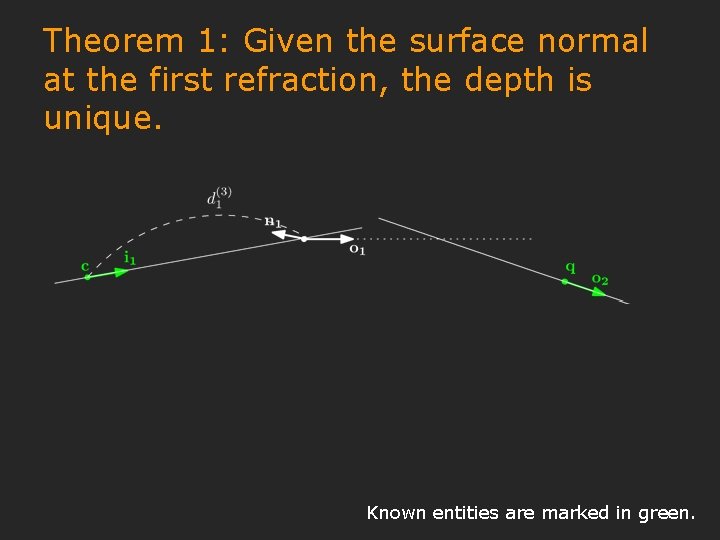
Theorem 1: Given the surface normal at the first refraction, the depth is unique. Known entities are marked in green.

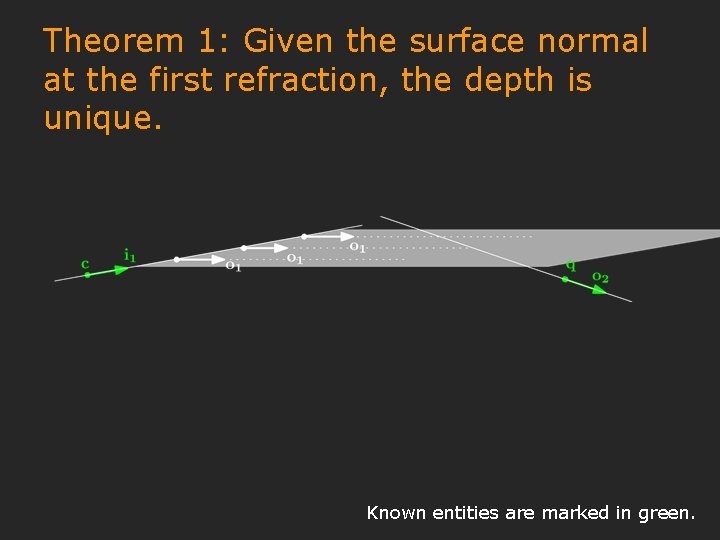
Theorem 1: Given the surface normal at the first refraction, the depth is unique. Known entities are marked in green.

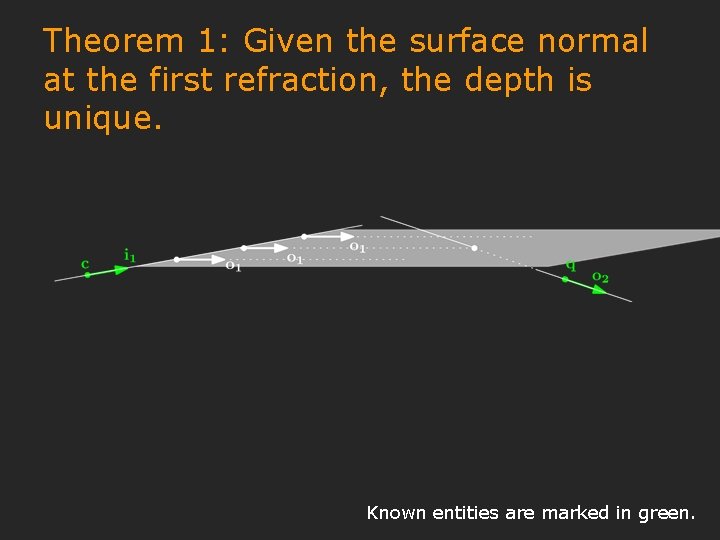
Theorem 1: Given the surface normal at the first refraction, the depth is unique. Known entities are marked in green.

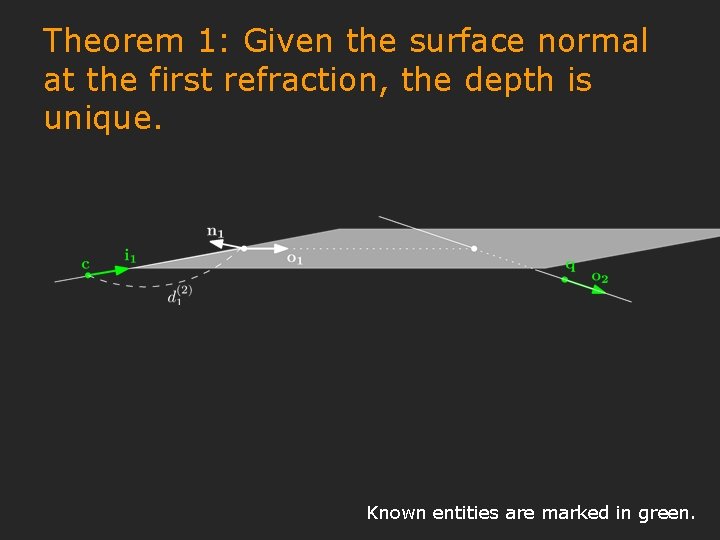
Theorem 1: Given the surface normal at the first refraction, the depth is unique. Known entities are marked in green.

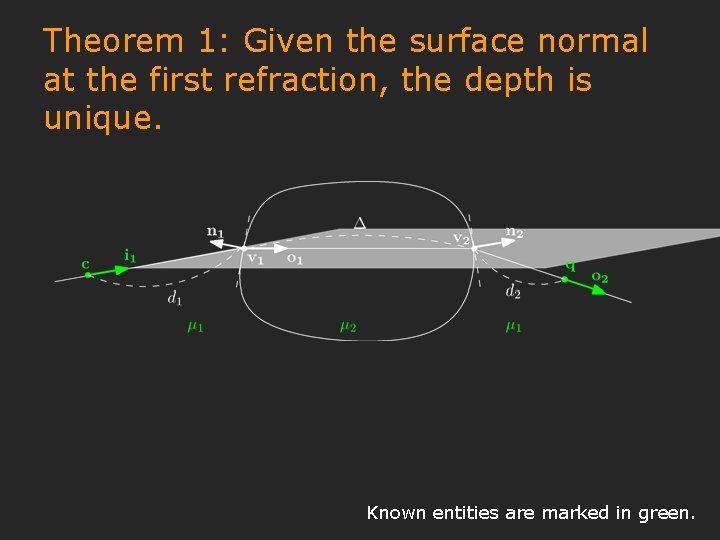
Theorem 1: Given the surface normal at the first refraction, the depth is unique. Known entities are marked in green.

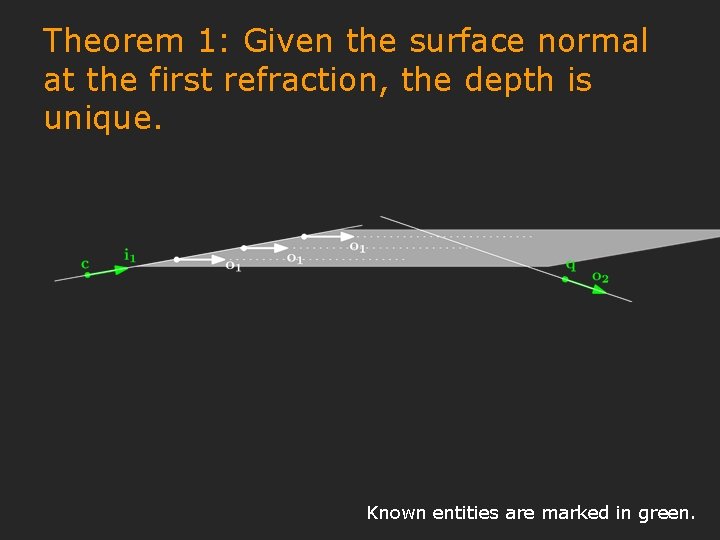
Theorem 1: Given the surface normal at the first refraction, the depth is unique. Known entities are marked in green.

Theorem 2: Given the surface depth at the first refraction, the normal is constrained to lie on a 1 D curve. Known entities are marked in green.

Theorem 2: Given the surface depth at the first refraction, the normal is constrained to lie on a 1 D curve. Known entities are marked in green.

Theorem 2: Given the surface depth at the first refraction, the normal is constrained to lie on a 1 D curve. Known entities are marked in green.

Theorem 2: Given the surface depth at the first refraction, the normal is constrained to lie on a 1 D curve. Known entities are marked in green.

Theorem 2: Given the surface depth at the first refraction, the normal is constrained to lie on a 1 D curve. Known entities are marked in green.

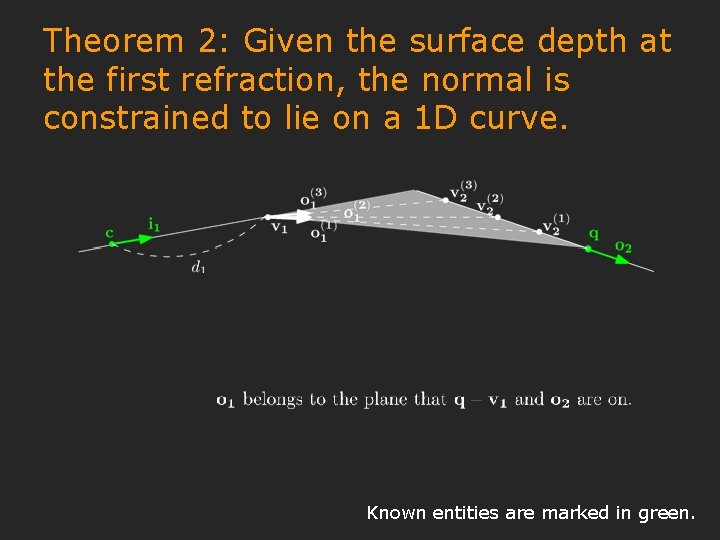
Theorem 2: Given the surface depth at the first refraction, the normal is constrained to lie on a 1 D curve. Known entities are marked in green.

Theorem 2: Given the surface depth at the first refraction, the normal is constrained to lie on a 1 D curve. Known entities are marked in green.

Theorem 2: Given the surface depth at the first refraction, the normal is constrained to lie on a 1 D curve. Known entities are marked in green.

Theorem 2: Given the surface depth at the first refraction, the normal is constrained to lie on a 1 D curve. Known entities are marked in green.

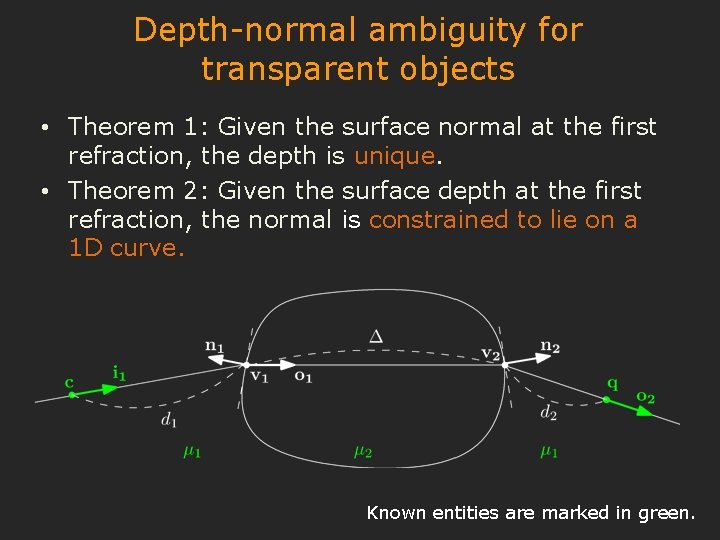
Depth-normal ambiguity for transparent objects • Theorem 1: Given the surface normal at the first refraction, the depth is unique. • Theorem 2: Given the surface depth at the first refraction, the normal is constrained to lie on a 1 D curve. Known entities are marked in green.

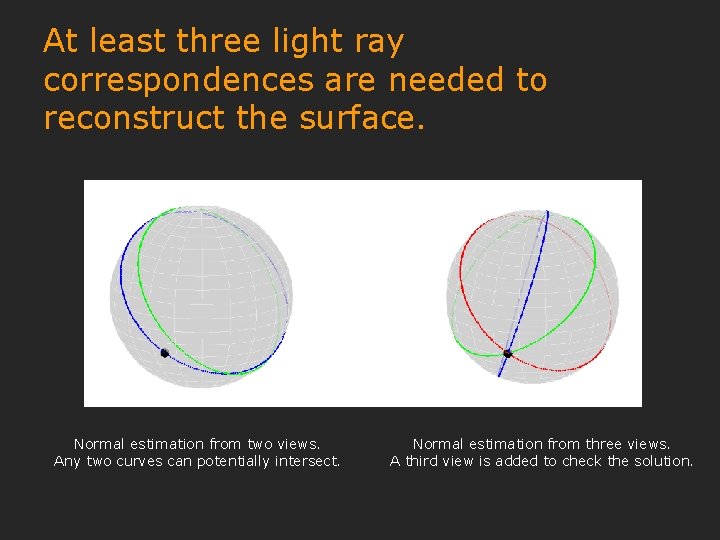
At least three light ray correspondences are needed to reconstruct the surface. Normal estimation from two views. Any two curves can potentially intersect. Normal estimation from three views. A third view is added to check the solution.

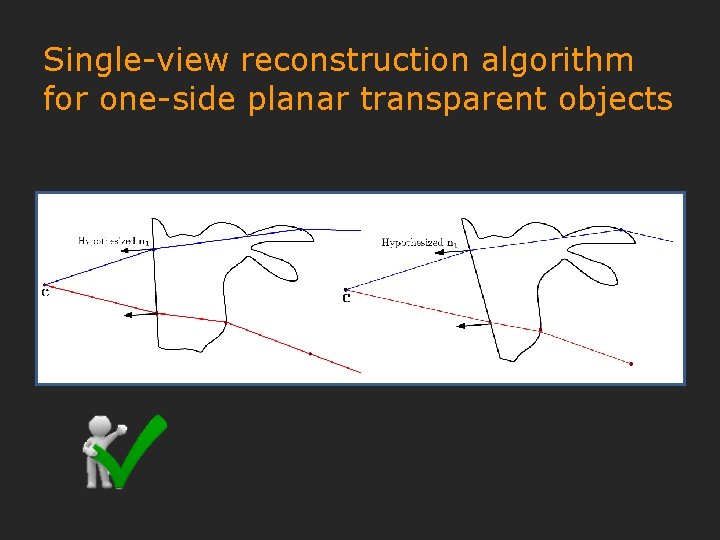
Single-view reconstruction algorithm for one-side planar transparent objects

data courtesy: Kutulakos and Steger, IJCV 2008

for more details, visit http: //imagesci. ece. cmu. edu