What do we know about the Standard Model

What do we know about the Standard Model? Sally Dawson Lecture 2 SLAC Summer Institute

The Standard Model Works • Any discussion of the Standard Model has to start with its success • This is unlikely to be an accident

Theoretical Limits on Higgs Sector • Unitarity – Really we mean perturbative unitarity – Violation of perturbative unitarity leads to consideration of strongly interacting models of EWSB such as technicolor, Higgless • Consistency of Standard Model – Triviality (What happens to couplings at high energy? ) – Does spontaneous symmetry breaking actually happen? • Naturalness – Renormalization of Higgs mass is different than renormalization of fermion mass – One motivation for supersymmetric models

Unitarity • Consider 2 2 elastic scattering s=center of mass energy-squared • Partial wave decomposition of amplitude • al are the spin l partial waves

Unitarity • Pl(cos ) are Legendre polynomials: Sum of positive definite terms

More on Unitarity • Optical theorem derived assuming only conservation of probability Im(al) • Unitarity requirement: Re(al)

More on Unitarity • Idea: Use unitarity to limit parameters of theory Cross sections which grow with energy always violate unitarity at some energy scale

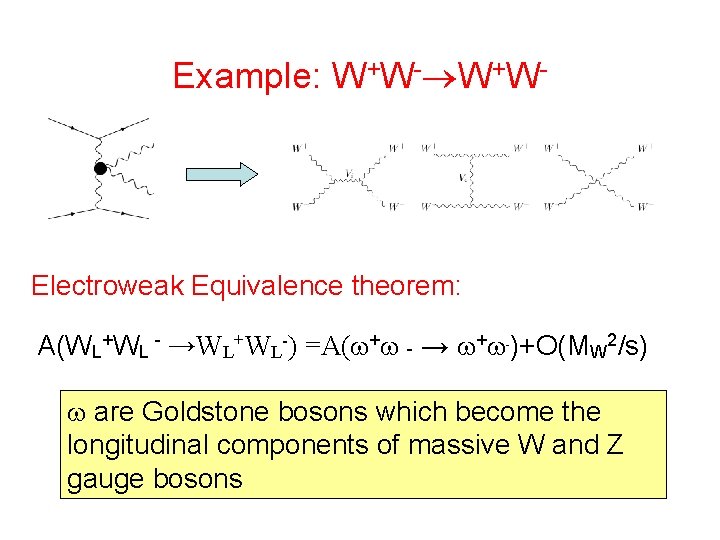
Example: W+W- Electroweak Equivalence theorem: A(WL+WL - →WL+WL-) =A( + - → + -)+O(MW 2/s) are Goldstone bosons which become the longitudinal components of massive W and Z gauge bosons

W+W- W+W • Consider Goldstone boson scattering: + - + • Recall scalar potential

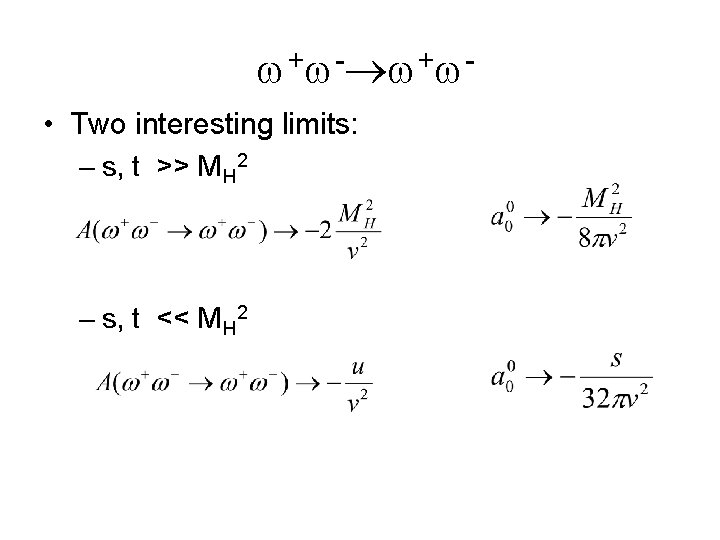
+ - + • Two interesting limits: – s, t >> MH 2 – s, t << MH 2

Use Unitarity to Bound Higgs • High energy limit: MH < 800 Ge. V • Heavy Higgs limit Ec 1. 7 Te. V New physics at the Te. V scale Can get more stringent bound from coupled channel analysis

Consider W+W- pair production Example: W+W (p) Ø t-channel amplitude: e(k) (q) Ø In center-of-mass frame: W +(p+) k=p-p+=p--q W -(p-)

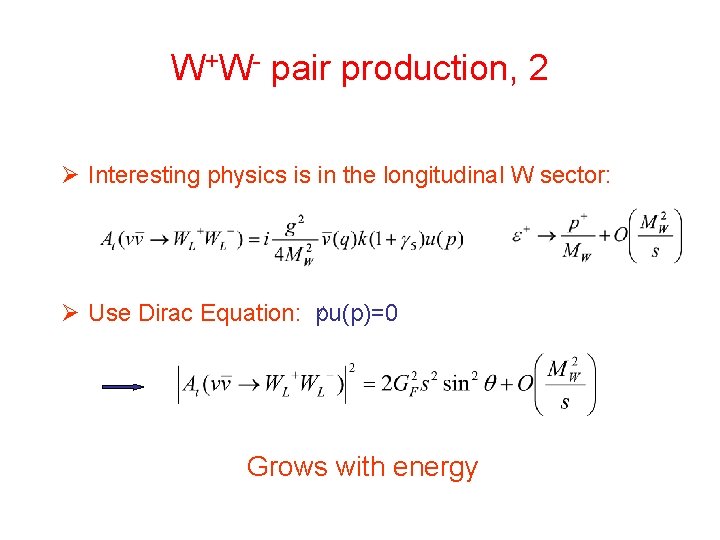
W+W- pair production, 2 Ø Interesting physics is in the longitudinal W sector: Ø Use Dirac Equation: pu(p)=0 Grows with energy

W+W- pair production, 3 Ø SM has additional contribution from s-channel Z exchange Ø For longitudinal W’s (p) (q) Contributions which grow with energy cancel between t- and schannel diagrams W +(p+) Z(k) W -(p-) Depends on special form of 3 -gauge boson couplings

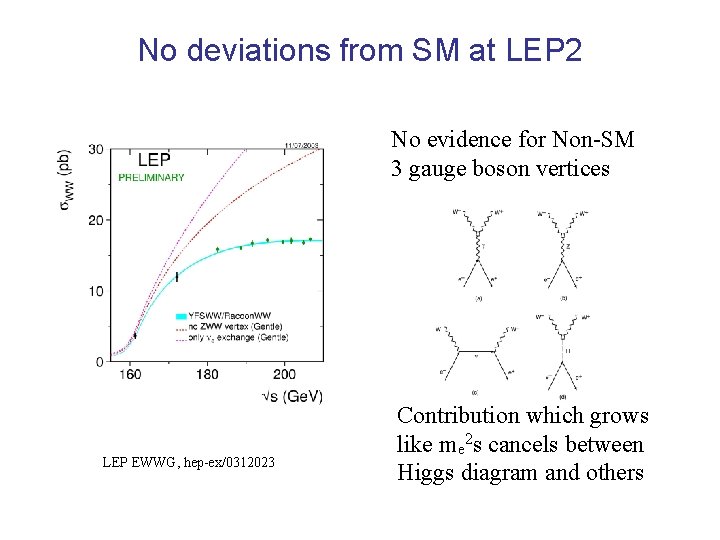
No deviations from SM at LEP 2 No evidence for Non-SM 3 gauge boson vertices LEP EWWG, hep-ex/0312023 Contribution which grows like me 2 s cancels between Higgs diagram and others

Limits on Scalar Potential • MH is a free parameter in the Standard Model • Can we derive limits on the basis of consistency? • Consider a scalar potential: • This is potential at electroweak scale • Parameters evolve with energy

High Energy Behavior of • Renormalization group scaling • Large (Heavy Higgs): self coupling causes to grow with scale • Small (Light Higgs): coupling to top quark causes to become negative

Does Spontaneous Symmetry Breaking Happen? • SM requires spontaneous symmetry • This requires • For small • Solve

Does Spontaneous Symmetry Breaking Happen? • ( ) >0 gives lower bound on MH • If Standard Model valid to 1016 Ge. V • For any given scale, , there is a theoretically consistent range for MH

What happens for large ? • Consider HH→HH • (Q) blows up as Q (called Landau pole)

Landau Pole • (Q) blows up as Q , independent of starting point • BUT…. Without H 4 interactions, theory is noninteracting • Require quartic coupling be finite • Requirement for 1/ (Q)>0 gives upper limit on Mh • Assume theory is valid to 1016 Ge. V – Gives upper limit of MH< 180 Ge. V

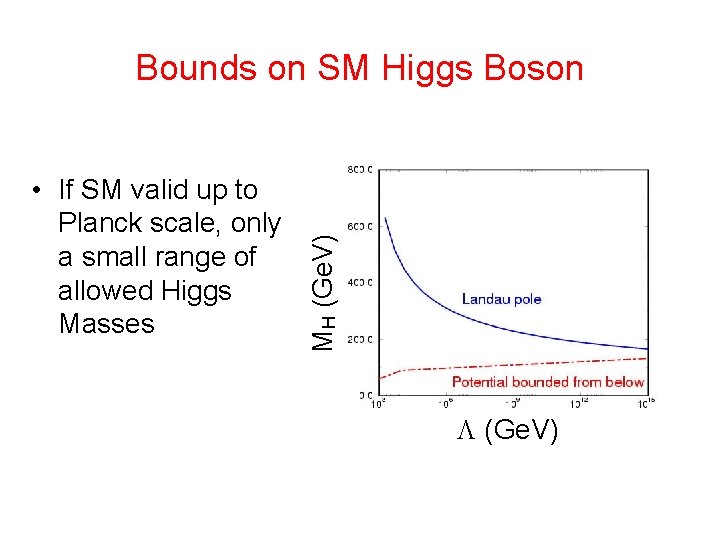
• If SM valid up to Planck scale, only a small range of allowed Higgs Masses MH (Ge. V) Bounds on SM Higgs Boson (Ge. V)

Naturalness • We often say that the SM cannot be the entire story because of the quadratic divergences of the Higgs Boson mass • Renormalization of scalar and fermion masses are fundamentally different

Masses at one-loop • First consider a fermion coupled to a massive complex Higgs scalar • Assume symmetry breaking as in SM:

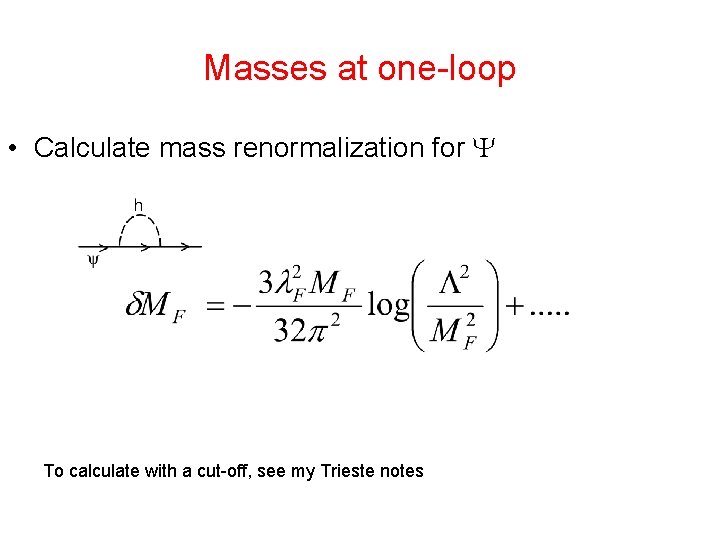
Masses at one-loop • Calculate mass renormalization for To calculate with a cut-off, see my Trieste notes

Symmetry and the fermion mass • MF – MF=0, then quantum corrections vanish – When MF=0, Lagrangian is invariant under • L ei L L • R ei R R – MF 0 increases the symmetry of theory – Yukawa coupling (proportional to mass) breaks symmetry and so corrections MF

Scalars are very different • MH diverges quadratically! • This implies quadratic sensitivity to high mass scales

Scalars • MH diverges quadratically • Requires large cancellations (hierarchy problem) • H does not obey decoupling theorem – Says that effects of heavy particles decouple as M • MH 0 doesn’t increase symmetry of theory – Nothing protects Higgs mass from large corrections

Light Scalars are Unnatural • Higgs mass grows with • No additional symmetry for MH=0, no protection from large corrections H H MH 200 Ge. V requires large cancellations

What’s the problem? • Compute Mh in dimensional regularization and absorb infinities into definition of MH • Perfectly valid approach • Except we know there is a high scale

Try to cancel quadratic divergences by adding new particles • SUSY models add scalars with same quantum numbers as fermions, but different spin • Little Higgs models cancel quadratic divergences with new particles with same spin

We expect something at the Te. V scale • If it’s a SM Higgs then we have to think hard about what the quadratic divergences are telling us • SM Higgs mass is highly restricted by requirement of theoretical consistency • Expect that Tevatron or LHC will observe SM Higgs (or definitively exclude it)