What are the real challenges in data mining

What are the real challenges in data mining? Charles Elkan University of California, San Diego August 21, 2003

Bogosity about learning with unbalanced data 1. The goal is yes/no classification. 1. No: ranking, or probability estimation 2. Often, P(c=minority|x) < 0. 5 for all examples x 2. Decision trees and C 4. 5 are well-suited – No: model each class separately, then use Bayes’ rule P(c|x) = P(x|c)P(c) / [ P (x|c)P(c) + P(x|~c)P(~c) ] – No: avoid small disjuncts With naïve Bayes: P(x|c) = P(xi | c) 3. Under/over-sampling are appropriate – No: do cost-based example-specific sampling, then bagging 4. ROC curves and AUC are important

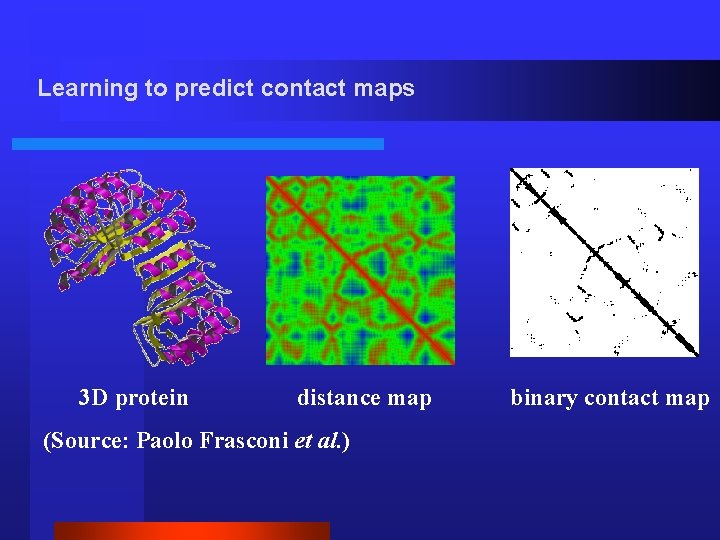
Learning to predict contact maps 3 D protein distance map (Source: Paolo Frasconi et al. ) binary contact map

Issues in contact map prediction An ML researcher sees O(n 2) non-contacts and O(n) contacts. 2. But to a biologist, the concept “an example of a noncontact” is far from natural. 3. Moreover, there is no natural probability distribution defining the population of “all” proteins. 4. A statistician sees simply O(n 2) distance measures— but s/he finds least-squares regression is useless! 1.

For the rooftop detection task … We used […] BUDDS, to extract candidate rooftops (I. e. parallelograms) from six-large area images. Such processing resulted in 17, 289 candidates, which an expert labeled as 781 positive examples and 17, 048 negative examples of the concept “rooftop. ” (Source: Learning When Data Sets are Imbalanced and When Costs are Unequal and Unknown, Marcus Maloof, this workshop. )

How to detect faces in real-time? Viola and Jones, CVPR ‘ 01: l. Slide window over image l 45396 features per window l. Learn boosted decisionstump classifier

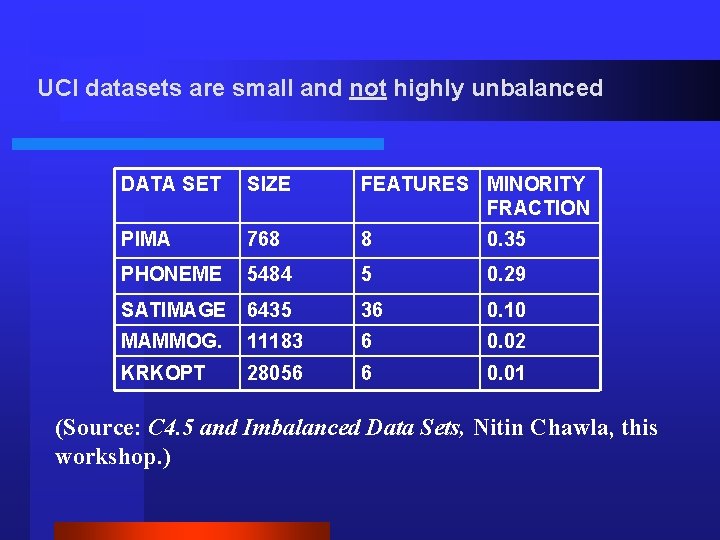
UCI datasets are small and not highly unbalanced DATA SET SIZE FEATURES MINORITY FRACTION PIMA 768 8 0. 35 PHONEME 5484 5 0. 29 SATIMAGE 6435 36 0. 10 MAMMOG. 11183 6 0. 02 KRKOPT 28056 6 0. 01 (Source: C 4. 5 and Imbalanced Data Sets, Nitin Chawla, this workshop. )

Features of the DMEF and similar datasets 1. 2. 3. 4. 5. 6. At least 105 examples and 102. 5 features. No single well-defined target class. Interesting cases have frequency < 0. 01. Much information on costs and benefits, but no overall model of profit/loss. Different cost matrices for different examples Most cost matrix entries are unknown.

Example-dependent costs and benefits actual legitimate predicted fraudulent legitimate + 0. 01 x -x fraudulent - 20 - 10 Observations: 1. Loss or profit depends on the transaction size x. 2. Figuring out the full profit/loss model is hard. 3. Opportunity costs are confusing. 4. Creative management transforms costs into benefits. 5. How do we account for long-term costs and benefits?

Correct decisions require correct probabilities actual legitimate predicted fraudulent legitimate + 0. 01 x -x fraudulent - 20 - 10 Let p = P(legitimate). The optimal decision is “approve” iff 0. 01 xp – (1 -p)x > (-20)p + (-10)(1 -p) This calculation requires well-calibrated estimates of p.

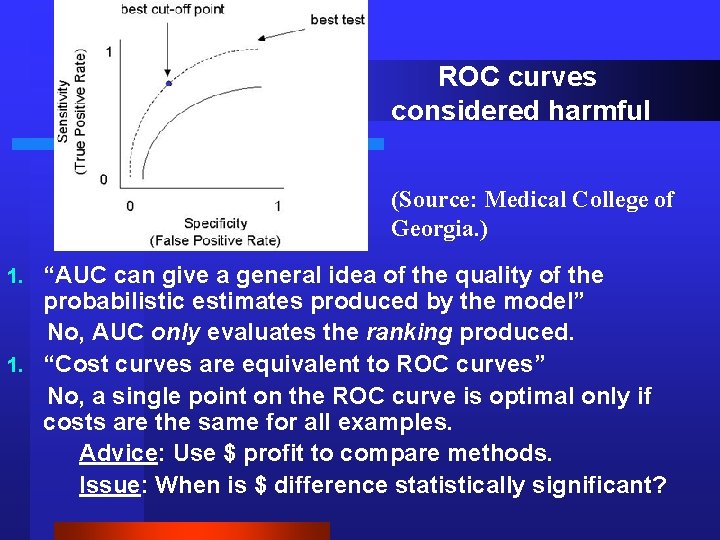
ROC curves considered harmful (Source: Medical College of Georgia. ) “AUC can give a general idea of the quality of the probabilistic estimates produced by the model” No, AUC only evaluates the ranking produced. 1. “Cost curves are equivalent to ROC curves” No, a single point on the ROC curve is optimal only if costs are the same for all examples. Advice: Use $ profit to compare methods. Issue: When is $ difference statistically significant? 1.

Usually we must learn a model to estimate costs actual donor predicted non-donor solicit x – $0. 68 - $0. 68 ignore 0 0 Cost matrix for soliciting donors to a charity. The donation amount x is always unknown for test examples, so we must use the training data to learn a regression model to predict x.

So, we learn a model to estimate costs … actual donor predicted non-donor solicit x – $0. 68 - $0. 68 ignore 0 0 Issue: The subset in the training set with x > 0 is a skewed sample for learning a model to estimate x. Reason: Donation amount x and probability of donation p are inversely correlated. Hence, the training set contains too few examples of large donations, compared to small ones.

The “reject inference” problem Let humans make credit grant/deny decisions. 2. Collect data about repay/write-off, but only for people to whom credit is granted. 3. Learn a model from this training data. 4. Apply the model to all future applicants. 1. Issue: “All future applicants” is a sample from a different population than “people to whom credit is granted. ”

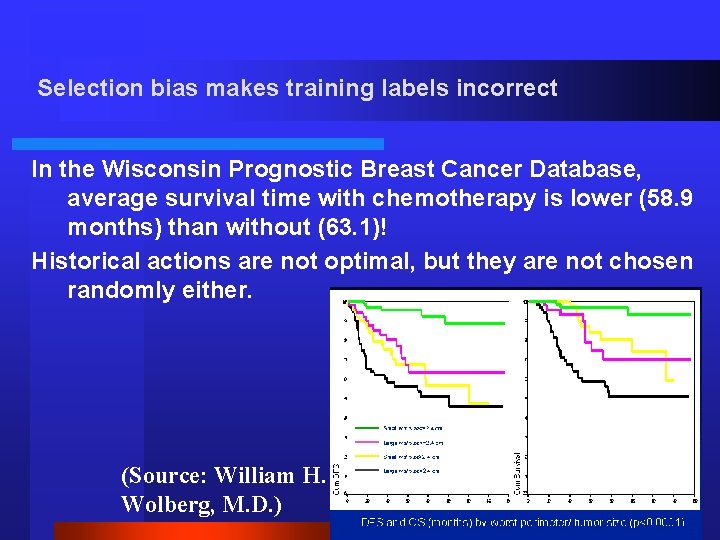
Selection bias makes training labels incorrect In the Wisconsin Prognostic Breast Cancer Database, average survival time with chemotherapy is lower (58. 9 months) than without (63. 1)! Historical actions are not optimal, but they are not chosen randomly either. (Source: William H. Wolberg, M. D. )

Sequences of training sets Use data collected in 2000 to learn a model; apply this model to select inside the 2001 population. 2. Use data about the individuals selected in 2001 to learn a new model; apply this model in 2002. 3. And so on… 1. Each time a new model is learned, its training set is has been created using a different selection bias.

Let’s use the word “unbalanced” in the future Google: Searched the web for imbalanced. … about 53, 800. Searched the web for unbalanced. … about 465, 000.

C. Elkan. The Foundations of Cost-Sensitive Learning IJCAI'01, pp. 973978. B. Zadrozny and C. Elkan. Learning and Making Decisions When Costs and Probabilities are Both Unknown KDD'01, pp. 204 -213. B. Zadrozny and C. Elkan. Obtaining Calibrated Probability Estimates from Decision Trees and Naive Bayesian Classifiers ICML'01, pp. 609 -616. N. Abe et al. Empirical Comparison of Various Reinforcement Learning Strategies for Sequential Targeted Marketing ICDM'02. B. Zadrozny, J. Langford, and N. Abe. Cost-Sensitive Learning by Cost. Proportionate Example Weighting ICDM’ 03.