What are the characteristics of DSP algorithms M

What are the characteristics of DSP algorithms? M. Smith and S. Daeninck DSP Introduction, M. Smith, ECE, University of Calgary, Canada

Tackled today What are the basic characteristics of a DSP algorithm? p Information on the Tiger. SHARC arithmetic, multiplier and shifter units p Practice examples of C++ to assembly code conversion p DSP Introduction, 2 M. Smith, ECE, University of Calgary, Canada

IEEE Micro Magazine Article p How RISCy is DSP? Smith, M. R. ; IEEE Micro, Volume: 12, Issue: 6, Dec. 1992, Pages: 10 - 23 Available on line via the library “Electronic web links” p Copy placed on ENCM 515 Web site. p n Make sure you read it before midterm 1 DSP Introduction, 3 M. Smith, ECE, University of Calgary, Canada

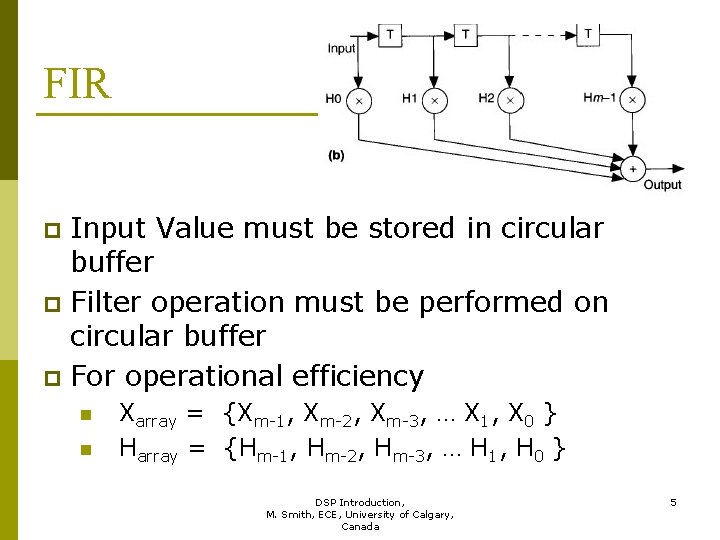
Characteristics of an FIR algorithm p Involves one of the three basic types of DSP algorithms n p FIR (Type 1), IIR (Type 2) and FFT (Type 3) Representative of DSP equations found in filtering, convolution and modeling n n n Multiplication / addition intensive Simple format within a (long) loop Many memory fetches of fixed and changing data Handle “infinite amount of input data” – need FIFO buffer when handling ON-LINE data All calculations “MUST” be completed in the time interval between samples DSP Introduction, 4 M. Smith, ECE, University of Calgary, Canada

FIR Input Value must be stored in circular buffer p Filter operation must be performed on circular buffer p For operational efficiency p n n Xarray = {Xm-1, Xm-2, Xm-3, … X 1, X 0 } Harray = {Hm-1, Hm-2, Hm-3, … H 1, H 0 } DSP Introduction, 5 M. Smith, ECE, University of Calgary, Canada

FIR p X[n – 1] = New. Input. Value n p p Sum = 0; For (count = 0 to N – 1) -- N of size 100+ n n n p p Into last place of Input Buffer Xvalue = X[count]; Hvalue = H[count]; Product = Xvalue * Hvalue; Sum = Sum + Product; Multiply and Accumulate -- MAC New. Output. Value = Sum; Update Buffer – The T-operation in the picture n For (count = 1 to N – 1) -- Discard oldest X[0]; p X[count – 1] = X[count]; DSP Introduction, 6 M. Smith, ECE, University of Calgary, Canada

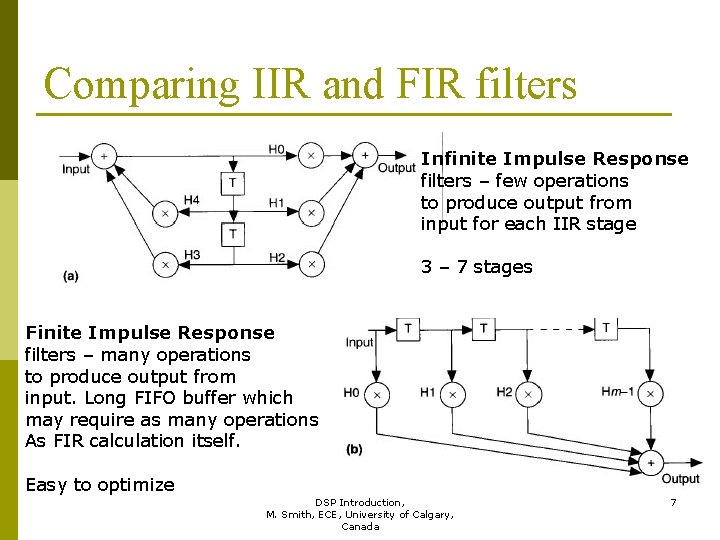
Comparing IIR and FIR filters Infinite Impulse Response filters – few operations to produce output from input for each IIR stage 3 – 7 stages Finite Impulse Response filters – many operations to produce output from input. Long FIFO buffer which may require as many operations As FIR calculation itself. Easy to optimize DSP Introduction, 7 M. Smith, ECE, University of Calgary, Canada

S 0 IIR -- Biquad S 1 S 2 p For (Stages = 0 to 3) Do n n p S 0 = Xin * H 5 + S 2 * H 3 + S 1 * H 4 Yout = S 0 * H 0 + S 1 * H 1 + S 2 * H 2 S 2 = S 1 = S 0 This second solution gives different result. The difference depends on how frequently samples are taken relative to how rapidly the signal changes n n n CALCULATION SPEED IS DIFFEREBR Yout = S 0 * H 0 + S 1 * H 1 + S 2 * H 2 S 2 = S 1 = S 0 = Xin * H 5 + S 2 * H 3 + S 1 * H 4 DSP Introduction, 8 M. Smith, ECE, University of Calgary, Canada

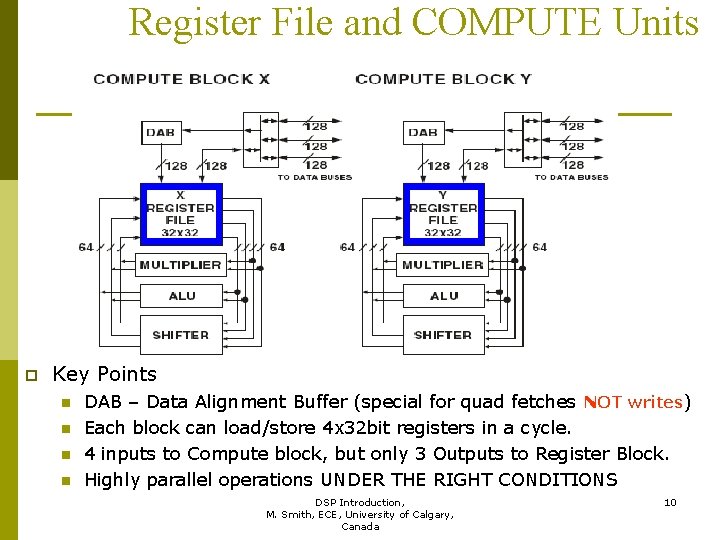
We need to know how the processor architecture affects speed of calculation Register File and Compute Block p Volatile registers p n n n Data Summation Multiply and Accumulate (MAC) DSP Introduction, 9 M. Smith, ECE, University of Calgary, Canada

Register File and COMPUTE Units p Key Points n n DAB – Data Alignment Buffer (special for quad fetches NOT writes) Each block can load/store 4 x 32 bit registers in a cycle. 4 inputs to Compute block, but only 3 Outputs to Register Block. Highly parallel operations UNDER THE RIGHT CONDITIONS DSP Introduction, 10 M. Smith, ECE, University of Calgary, Canada

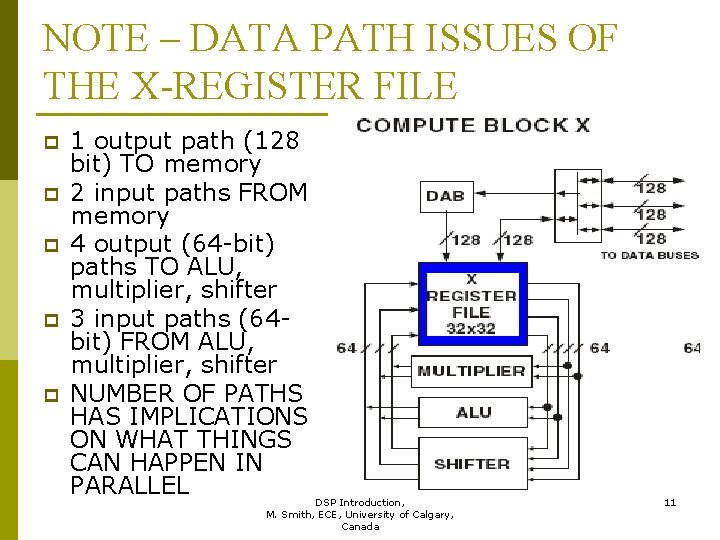
NOTE – DATA PATH ISSUES OF THE X-REGISTER FILE p p p 1 output path (128 bit) TO memory 2 input paths FROM memory 4 output (64 -bit) paths TO ALU, multiplier, shifter 3 input paths (64 bit) FROM ALU, multiplier, shifter NUMBER OF PATHS HAS IMPLICATIONS ON WHAT THINGS CAN HAPPEN IN PARALLEL DSP Introduction, 11 M. Smith, ECE, University of Calgary, Canada

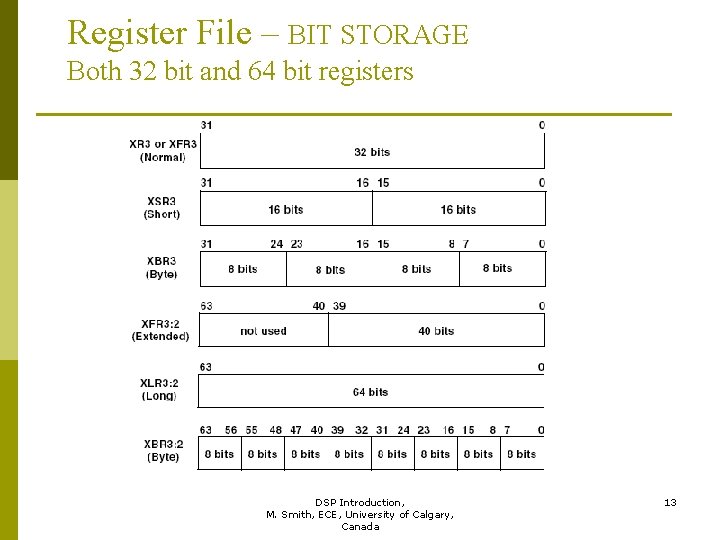
Register File - Syntax p Key Points n n n Each Block has 32 x 32 bit Data registers Each register can store 4 x 8 bit, 2 x 16 bit or 1 x 32 bit words. Registers can be combined into dual or quad groups. These groups can store 8, 16, 32, 40 or 64 bit words. XR 7 -> 1 x 32 bit word XLR 7: 6 -> 1 x 64 bit word XFR 1: 0 -> 1 x 40 bit float XSR 3: 2 -> 4 x 16 bit words Multiple of 2 XBR 3: 0 -> 16 x 8 bit words Register Syntax Multiple of 4 DSP Introduction, 12 M. Smith, ECE, University of Calgary, Canada

Register File – BIT STORAGE Both 32 bit and 64 bit registers DSP Introduction, 13 M. Smith, ECE, University of Calgary, Canada

Volatile Data Registers Non-preserved during a function call Volatile registers – no need to save p 24 Volatile DATA registers in each block p n n p 2 ALU SUMMATION registers in each block n p XR 0 – XR 23 YR 0 – YR 23 XPR 0, XPR 1, YPR 0, YPR 1 5 MAC ACCUMULATE registers in each block n n XMR 0 – XMR 3, YMR 0 – YMR 3 XMR 4, YMR 4 – Overflow registers DSP Introduction, 14 M. Smith, ECE, University of Calgary, Canada

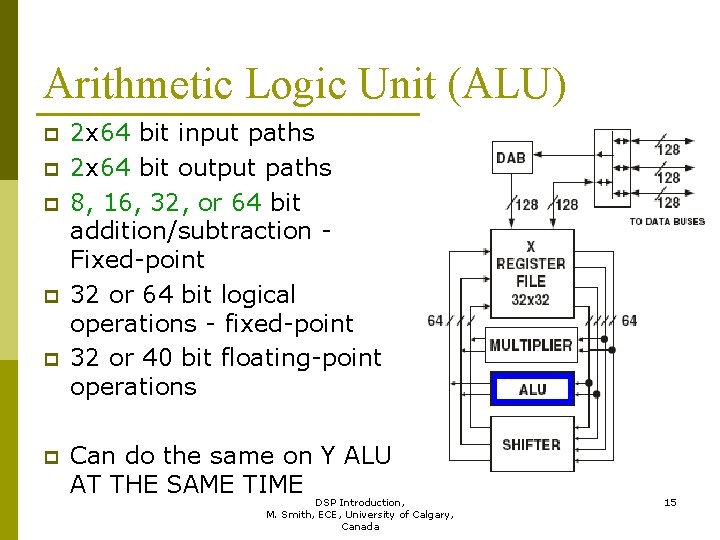
Arithmetic Logic Unit (ALU) p p p 2 x 64 bit input paths 2 x 64 bit output paths 8, 16, 32, or 64 bit addition/subtraction - Fixed-point 32 or 64 bit logical operations - fixed-point 32 or 40 bit floating-point operations Can do the same on Y ALU AT THE SAME TIME DSP Introduction, 15 M. Smith, ECE, University of Calgary, Canada

Sample ALU Instruction Example of 16 bit addition XYSR 1: 0 = R 31: 30 + R 25: 24 Performs “short” addition in X and Y Compute Blocks XR 1. HH = XR 31. HH + XR 25. HH XR 1. HL = XR 31. HL + XR 25. HL XR 0. LH = XR 30. LH + XR 24. LH XR 0. LL = XR 30. LL + XR 24. LL YR 1. HH = YR 31. HH + YR 25. HH YR 1. HL = YR 31. HL + YR 25. HL YR 0. LH = YR 30. LH + YR 24. LH YR 0. LL = YR 30. LL + YR 24. LL 8 additions at the same time. LH, . HH is my notation DSP Introduction, 16 M. Smith, ECE, University of Calgary, Canada

Sample ALU Instructions Fixed-Point Floating-Point long word, short Single, double precision DSP Introduction, 17 word, byte (char) M. Smith, ECE, University of Calgary, Canada

Pass is an interesting instruction p XR 4 = R 5 n p Assignment statement -- makes XR 4 XR 5 XR 4 = PASS R 5 n n n Still makes XR 4 XR 5 BUT USES A DIFFERENT PATH THROUGH THE PROCESSOR Sets the ALU flags (so that they can be used for conditional tests) PASS instructions can be put in parallel with different instructions than assignments DSP Introduction, 18 M. Smith, ECE, University of Calgary, Canada

Example int x_two = 64, y_two = 16; int x_three = 128, y_three = 8; int x_four = 128, y_four = 8; int x_five = 64, y_five = 16; int x_odd = 0, y_odd = 0; int x_even = 0, y_even = 0; XR 2 = 64; ; XR 3 = 128; ; XR 4 = 128; ; XR 5 = 64; ; YR 2 = 16; ; YR 3 = 8; ; YR 4 = 8; ; YR 5 = 16; ; x_odd = x_five + x_three; x_even = x_four + x_two; y_odd = y_five + y_three; y_even = y_four + y_two; XYR 1: 0 = R 5: 4 + R 3: 2; ; //XR 1 = x_odd, XR 0 = x_even //YR 1 = y_odd, YR 1 = y_even DSP Introduction, 19 M. Smith, ECE, University of Calgary, Canada

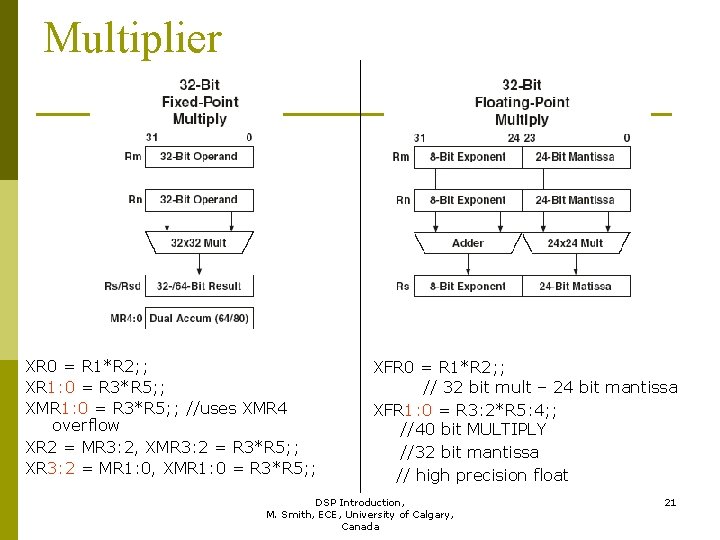
Multiplier p p Operates on fixed, floating and complex numbers. Fixed-Point numbers n n n p Floating-Point numbers n n p 32 x 32 bit with 32 or 64 bit results 4 (16 x 16 bit) with 4 x 16 or 4 x 32 bit results Data compaction inputs – 16, 32, 64 bits, outputs 16, 32 bit results 32 x 32 bit with 32 bit result 40 x 40 bit with 40 bit result COMPLEX Numbers n n 32 x 32 bit with results stored in MR register FIXED-POINT ONLY DSP Introduction, 20 M. Smith, ECE, University of Calgary, Canada

Multiplier XR 0 = R 1*R 2; ; XR 1: 0 = R 3*R 5; ; XMR 1: 0 = R 3*R 5; ; //uses XMR 4 overflow XR 2 = MR 3: 2, XMR 3: 2 = R 3*R 5; ; XR 3: 2 = MR 1: 0, XMR 1: 0 = R 3*R 5; ; XFR 0 = R 1*R 2; ; // 32 bit mult – 24 bit mantissa XFR 1: 0 = R 3: 2*R 5: 4; ; //40 bit MULTIPLY //32 bit mantissa // high precision float DSP Introduction, 21 M. Smith, ECE, University of Calgary, Canada

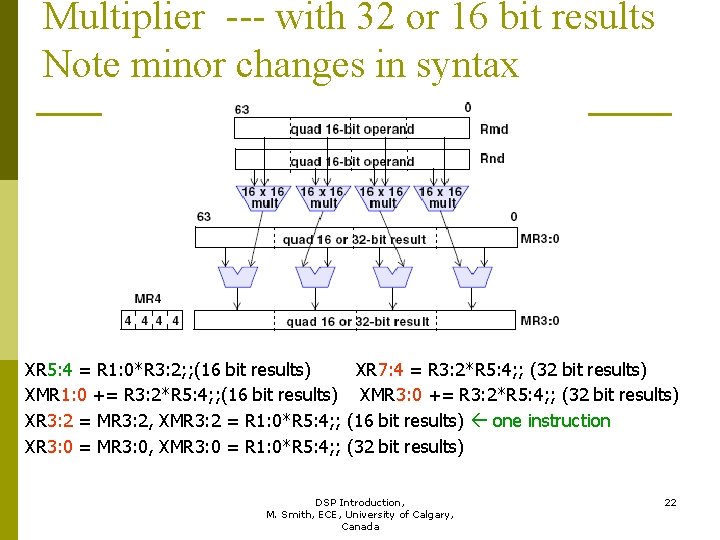
Multiplier --- with 32 or 16 bit results Note minor changes in syntax XR 5: 4 = R 1: 0*R 3: 2; ; (16 bit results) XR 7: 4 = R 3: 2*R 5: 4; ; (32 bit results) XMR 1: 0 += R 3: 2*R 5: 4; ; (16 bit results) XMR 3: 0 += R 3: 2*R 5: 4; ; (32 bit results) XR 3: 2 = MR 3: 2, XMR 3: 2 = R 1: 0*R 5: 4; ; (16 bit results) one instruction XR 3: 0 = MR 3: 0, XMR 3: 0 = R 1: 0*R 5: 4; ; (32 bit results) DSP Introduction, 22 M. Smith, ECE, University of Calgary, Canada

Practice Examples Convert from “C” into assembly code – use volatile registers BAD DESIGN OF FLOATING PT CODE WILL INTRODUCE MANY ERRORS RE-WRITE CODE TO FIX long int value = 6; long int number = 7; long int temp = 8; value = number * temp; float value = 6; float number = 7; long int temp = 8; value = number * temp; DSP Introduction, 23 M. Smith, ECE, University of Calgary, Canada

Avoiding common design errors Convert from “C” into assembly code – use volatile registers float value = 6. 0; (XFR 12) float number = 7. 0; (XFR 13) long int temp = 8; (XR 18) value = number * temp; // Treat as value = number * (float) temp; XR 12 = 6. 0; ; //value. F 12 // Sets XFR 12 6. 0 XR 13 = 7. 0; ; //number. F 13 XR 18 = 8; ; //temp. R 18 //(float) temp. R 18 XFR 18 = FLOAT R 18; ; //value. F 12 = number. F 13 * temp. F 18 XFR 12 = R 13 * R 18; ; DSP Introduction, 24 M. Smith, ECE, University of Calgary, Canada

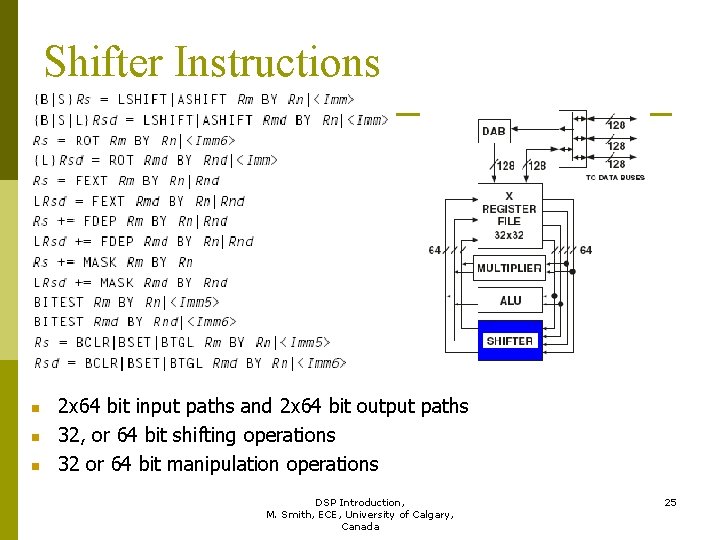
Shifter Instructions n n n 2 x 64 bit input paths and 2 x 64 bit output paths 32, or 64 bit shifting operations 32 or 64 bit manipulation operations DSP Introduction, 25 M. Smith, ECE, University of Calgary, Canada

Examples --- shift only integers There is a FSCALE for floats (not shifter) long int value = 128; long int high, low; XR 0 = 2; ; XR 1 = -XR 2; ; XR 2 = 128; ; low = value >> 2; high = value << 2; //low = value >> 2; XR 23 = ASHIFT XR 2 BY – 2; ; Or XR 23 = ASHIFT XR 2 BY XR 1; ; POSITIVE VALUE – LEFT SHIFT NEGATIVE VALUE – RIGHT SHIFT //high = value << 2; XR 22 = ASHIFT XR 2 BY 2; ; Or XR 22 = ASHIFT XR 2 BY XR 0; ; DSP Introduction, 26 M. Smith, ECE, University of Calgary, Canada

ALU instructions p Under the RIGHT conditions can do multiple operations in a single instruction. n n Instruction line has 4 x 32 bit instruction slots. Can do 2 Compute and 2 memory operations. This is actually 4 Compute operations counting both compute blocks. One instruction per unit of a compute block, ie. ALU. Since there are only 3 result buses, only one unit (ALU or Multiplier) can use 2 result buses. Not all instructions can be used in parallel. n p DSP Introduction, 27 M. Smith, ECE, University of Calgary, Canada

Dual Operation Examples p FRm = Rx + Ry, FRn = Rx – Ry; ; n n n p Note that uses 4(8) different registers and not 6(12) p FR 4 = R 2 + R 1, FR 5 = R 2 - R 1; ; The source registers used around the + and – must be the same. Very useful in FFT code Can be floating(single or extended precision) or fixed(32 or 64 bit) add/subtract. Rm = MRa, MRa += Rx * Ry; ; n n n MRa must be the same register(s) (MR 1: 0 or MR 3: 2) Can be used on fixed(32 or 64 bit results) COMPLEX numbers (on 16 bit values) p Rm = MRa, MRa += Rx ** Ry; ; DSP Introduction, 28 M. Smith, ECE, University of Calgary, Canada

Practice Examples Convert to assembly code Convert from “C” into assembly code – use volatile registers #define value_XR 12 Assignment operation value_XR 12 = 6; ; Multiply operations value_XR 12 = R 5 * R 6; long int value = 6; long int number = 7; long int temp = 8; value = number * temp; DSP Introduction, 29 M. Smith, ECE, University of Calgary, Canada

Avoiding common design errors Convert to assembly code float value = 6. 0; float number = 7. 0; long int temp = 8; value = value + 1; number = number + 2; temp = value + number; DSP Introduction, 30 M. Smith, ECE, University of Calgary, Canada

Tackled today What are the basic characteristics of a DSP algorithm? p Information on the Tiger. SHARC arithmetic, multiplier and shifter units p Practice examples of C++ to assembly code conversion p DSP Introduction, 31 M. Smith, ECE, University of Calgary, Canada