What are roots of the Wilkinson polynomial Zhonggang

What are roots of the Wilkinson polynomial? Zhonggang Zeng Northeastern Illinois University May 12, 2001

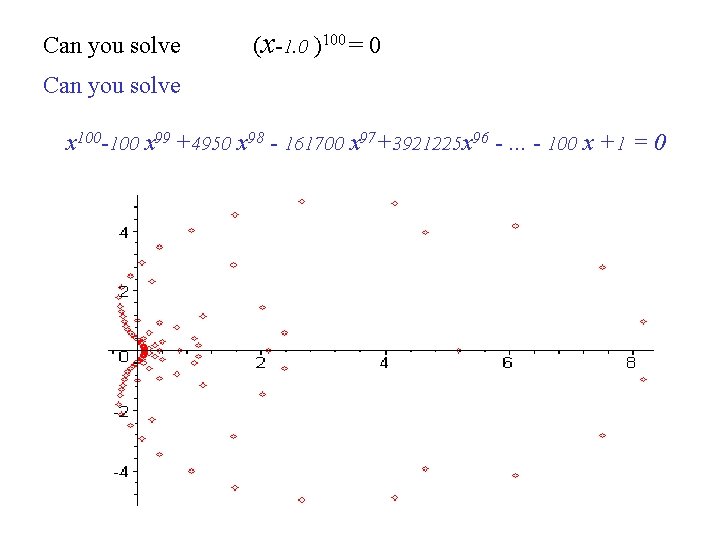
Can you solve (x-1. 0 )100 = 0 Can you solve x 100 -100 x 99 +4950 x 98 - 161700 x 97+3921225 x 96 -. . . - 100 x +1 = 0

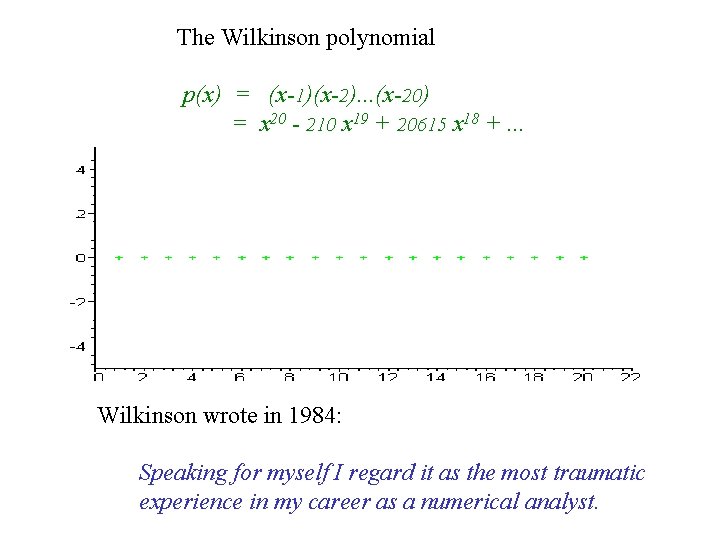
The Wilkinson polynomial p(x) = (x-1)(x-2). . . (x-20) = x 20 - 210 x 19 + 20615 x 18 +. . . Wilkinson wrote in 1984: Speaking for myself I regard it as the most traumatic experience in my career as a numerical analyst.

Classical textook methods for multiple roots Newton’s iteration xj+1 = xj - f(xj)/f’(xj), j=0, 1, 2, . . . converges locally to a multiple root of f(x) with a linear rate. The modified Newton’s iteration xj+1 = xj - mf(xj)/f’(xj), j=0, 1, 2, . . . converges locally to a m-fold root of f(x) with a quadratic rate. Newton’s iteration applied to g(x) = f(x)/f’(x) converges locally and quadratically to a root of f(x) regardliss of its multiplicity. None of them work!

Example: f(x) = (x-2)7(x-3)(x-4) in expanded form. Modified Newton’s iteration with m = 7 intended for root x = 2: x 1 = 1. 9981 x 2 = 1. 7481 x 3 = 1. 9892 x 4 = 0. 4726 x 5 = 1. 8029 x 6 = 1. 9931 x 7 = 4. 2681 x 8 = 3. 3476. . .

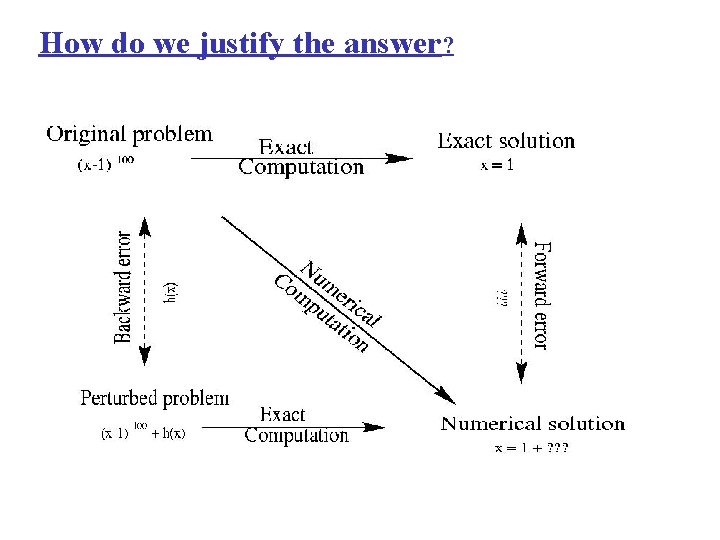
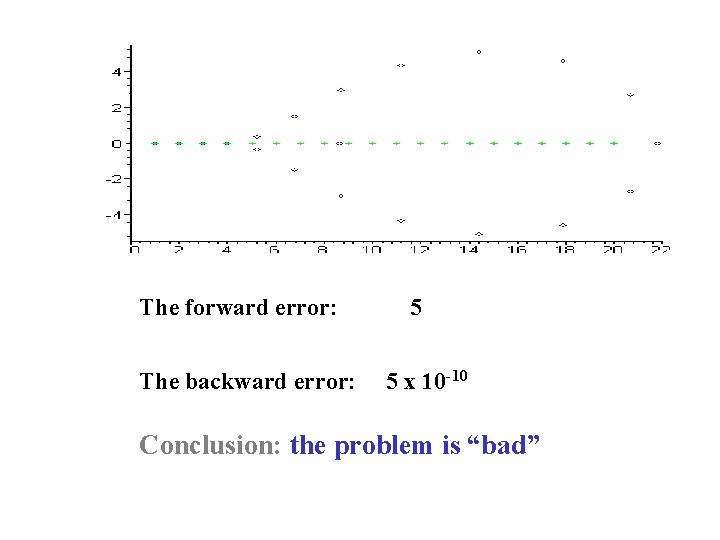
How do we justify the answer?

The forward error: The backward error: 5 5 x 10 -10 Conclusion: the problem is “bad”

If the answer is highly sensitive to perturbations, you have probably asked the wrong question. Maxims about numerical mathematics, computers, science and life, L. N. Trefethen. SIAM News Who is asking a wrong question? A: “Customer” B: Numerical analyst A: The polynomial What is the wrong question? B: The computing subject

The question we used to ask: Given a polynomial p(x) = xn + a 1 xn-1+. . . +an-1 x + an find ( z 1, . . . , zn ) such that p(x) = ( x - z 1 )( x - z 2 ). . . ( x - zn ) Right - or - Wrong ?

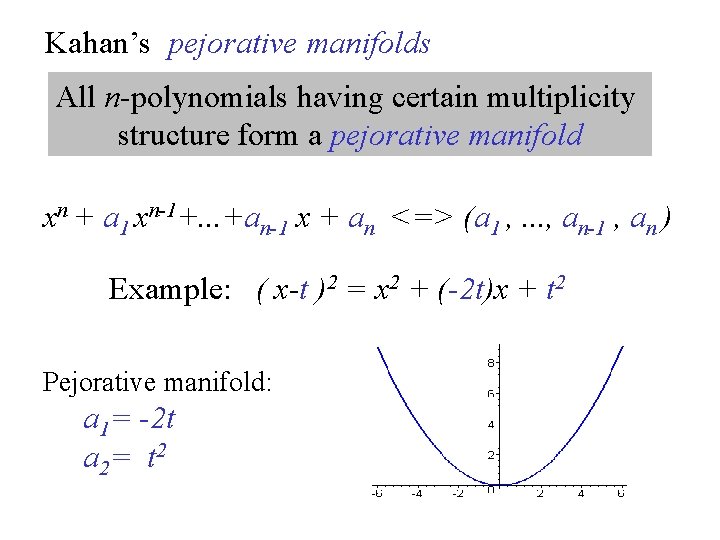
Kahan’s pejorative manifolds All n-polynomials having certain multiplicity structure form a pejorative manifold xn + a 1 xn-1+. . . +an-1 x + an <=> (a 1 , . . . , an-1 , an ) Example: ( x-t )2 = x 2 + (-2 t)x + t 2 Pejorative manifold: a 1= -2 t a 2= t 2

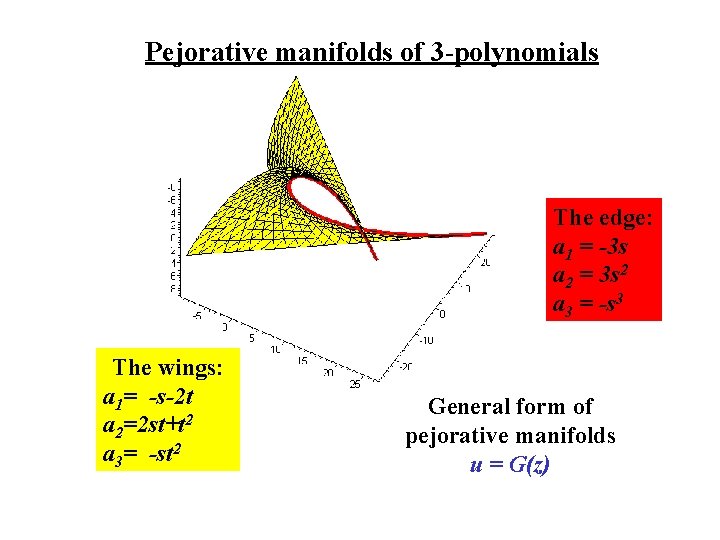
Pejorative manifolds of 3 -polynomials The edge: a 1 = -3 s a 2 = 3 s 2 a 3 = -s 3 The wings: a 1= -s-2 t a 2=2 st+t 2 a 3= -st 2 General form of pejorative manifolds u = G(z)

W. Kahan, Conserving confluence curbs ill-condition, 1972 1. Ill-condition occurs when a polynomial is near a pejorative manifold. 2. A small “drift” by a polynomial on that pejorative manifold does not cause large forward error to the multiple roots, except 3. If a multiple root is sensitive to small perturbation on the pejorative manifold, then the polynomial is near a pejorative submanifold of higher multiplicity. Ill-condition is caused by solving polynomial equations on a wrong manifold

Given a polynomial p(x) = xn + a 1 xn-1+. . . +an-1 x + an The wrong question: /Find / / / (/ z/1, /. . . , / z/n )/ such / / / that / / /p(x) / / =/ (/ x/ - /z 1/)(/ x/ - /z 2/) /. . . /( /x -/ z/n )/ because you are asking for simple roots! The right question: Find ( z 1, . . . , zm ) such that p(x) = ( x - z 1 ) s 1( x - z 2 )s 2. . . ( x - zm )sm s 1+. . . + sm = n, m < n do it on the pejorative manifold!

For ill-conditioned polynomial p(x)= xn + a 1 xn-1+. . . +an-1 x + an ~ a = (a 1 , . . . , an-1 , an ) The objective: find u*=G(z*) that is nearest to p(x)~a

Let ( x - z 1 ) s 1( x - z 2 )s 2. . . ( x - zm )sm = xn + g 1 ( z 1, . . . , zm ) xn-1+. . . +gn-1 ( z 1, . . . , zm ) x + gn ( z 1, . . . , zm ) Then, p(x) = ( x - z 1 ) s 1( x - z 2 )s 2. . . ( x - zm )sm g 1 ( z 1, . . . , zm ) =a 1 g 2( z 1, . . . , zm ) =a 2. . gn ( z 1, . . . , zm ) =an I. e. An over determined polynomial system G(z) = a <==>

The Gauss-Newton iteration zi+1=zi - J(zi )+[ G(zi )-a ], i=0, 1, 2. . .

zi+1=zi - J(zi )+[ G(zi )-a ], i=0, 1, 2. . . Theorem: If z=(z 1, . . . , zm) with z 1, . . . , zm distinct, then the Jacobian J(z) of G(z) is of full rank. Theorem: Let u*=G(z*) be nearest to p(x)~a, if 1. z*=(z*1, . . . , z*m) with z*1, . . . , z*m distinct; 2. z 0 is sufficiently close to z*; 3. a is sufficiently close to u* then the Gauss-Newton iteration converges with a linear rate. Further assume that a = u* , then the convergence is quadratic.

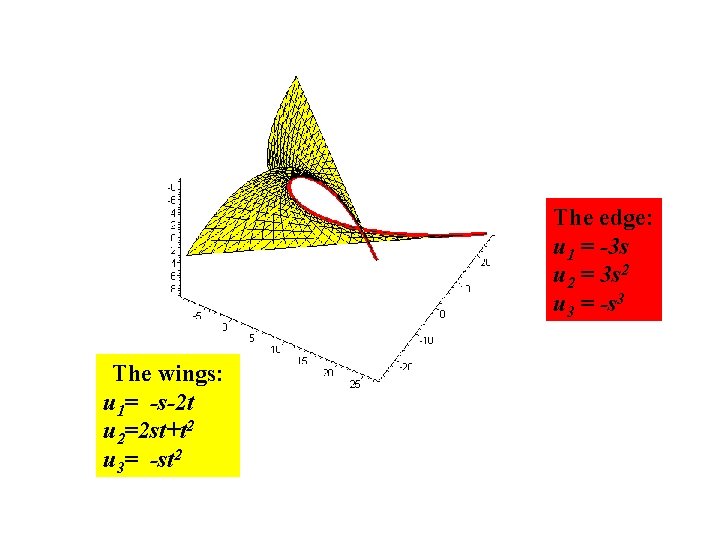
The edge: u 1 = -3 s u 2 = 3 s 2 u 3 = -s 3 The wings: u 1= -s-2 t u 2=2 st+t 2 u 3= -st 2

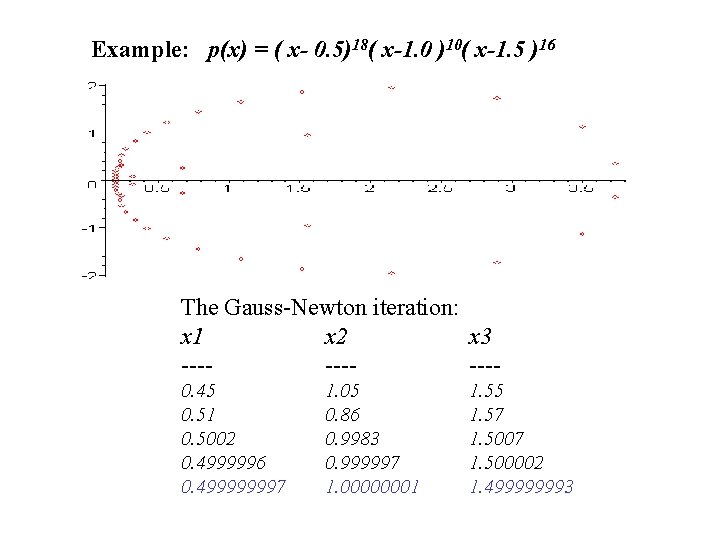
Example: p(x) = ( x- 0. 5)18( x-1. 0 )10( x-1. 5 )16 The Gauss-Newton iteration: x 1 x 2 x 3 -----0. 45 0. 51 0. 5002 0. 4999996 0. 499999997 1. 05 0. 86 0. 9983 0. 999997 1. 00000001 1. 55 1. 57 1. 500002 1. 499999993

What are the roots of the Wilkinson polynomial? (x-1)(x-2). . . (x-19)(x-20) ~ (x-z 1 )(x-z 2 )(x-z 3 )2(x-z 4 )3(x-z 5 )4(x-z 6 )4(x-z 7 )3(x-z 8 )2 Where roots 1. 00031227 1. 98468140 3. 36763082 5. 99316993 9. 29701289 13. 85522338 16. 66437572 19. 84916622 multiplicity + + ++ ++++ +++ ++ These roots are not sensitive to perturbation

Conclusion Ill-condition is caused by a wrong “identity”. Multiple roots are stable and can be computed with high accuracy, if they are calculated on a proper pejorative manifold. As a related work, isolated multiple roots/eigenvalues can be computed as simple, stable zeros of an extended polynomial system with high accuracy.