Well Testing Module 6 Well Test Analysis of

Well Testing Module #6: Well Test Analysis of Naturally Fractured Reservoirs Shahab Gerami, Ph. D 1 S. Gerami 1

Outline • Introduction • Porosity and permeability of fractured reservoirs • Fluid exchange • Radial well in naturally fractured reservoir • Characteristic of a fractured reservoir • Buildup and Drawdown behavior • Mathematical model (Warren and Root) • Important features of other models S. Gerami 2

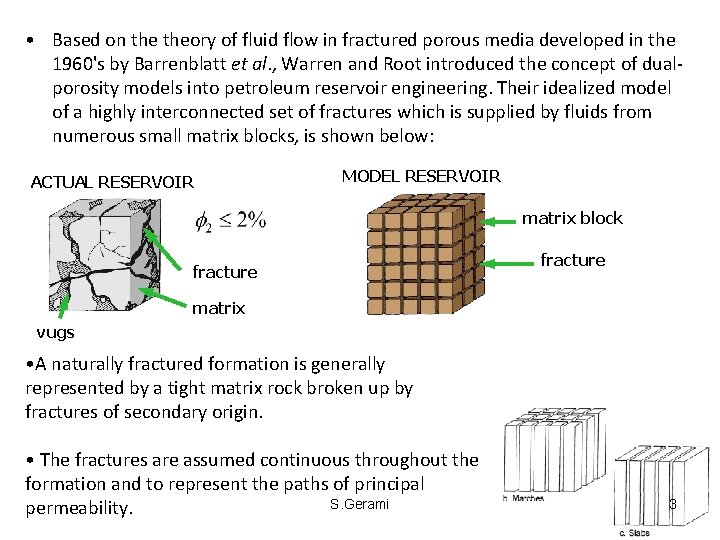
• Based on theory of fluid flow in fractured porous media developed in the 1960's by Barrenblatt et al. , Warren and Root introduced the concept of dualporosity models into petroleum reservoir engineering. Their idealized model of a highly interconnected set of fractures which is supplied by fluids from numerous small matrix blocks, is shown below: ACTUAL RESERVOIR MODEL RESERVOIR matrix block fracture matrix vugs • A naturally fractured formation is generally represented by a tight matrix rock broken up by fractures of secondary origin. • The fractures are assumed continuous throughout the formation and to represent the paths of principal S. Gerami permeability. 3

Porosity and Permeability • Whereas the matrix permeability is much smaller than the fracture permeability, the fracture porosity of a particular class of naturally fractured reservoirs seldom exceeds 1. 5% or 2%, and usually falls below 1%. • The high permeability of a fracture results in a high diffusivity of the pressure propagation pulse along the fracture. A fracture of 0. 1 mm will have a permeability of 833 darcys, whereas the permeability of the limestone proper will usually be of the order of 0. 01 darcy. (Muskat (1937), pp. 425) S. Gerami 4

S. Gerami 5

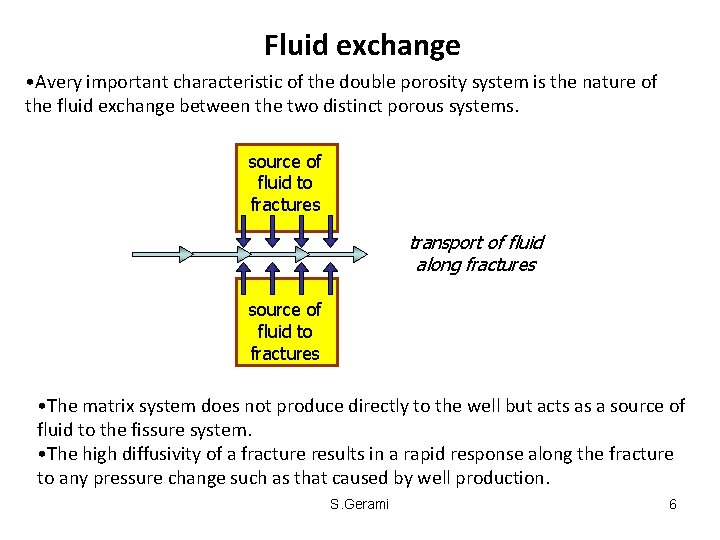
Fluid exchange • Avery important characteristic of the double porosity system is the nature of the fluid exchange between the two distinct porous systems. source of fluid to fractures transport of fluid along fractures source of fluid to fractures • The matrix system does not produce directly to the well but acts as a source of fluid to the fissure system. • The high diffusivity of a fracture results in a rapid response along the fracture to any pressure change such as that caused by well production. S. Gerami 6

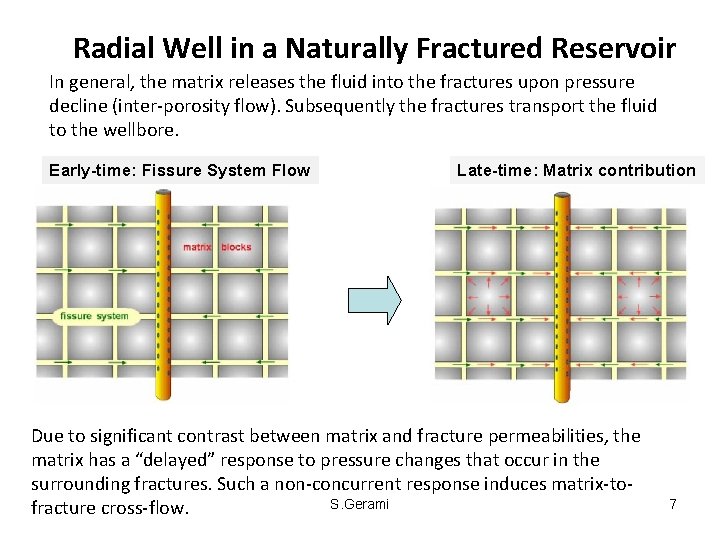
Radial Well in a Naturally Fractured Reservoir In general, the matrix releases the fluid into the fractures upon pressure decline (inter-porosity flow). Subsequently the fractures transport the fluid to the wellbore. Early-time: Fissure System Flow Late-time: Matrix contribution Due to significant contrast between matrix and fracture permeabilities, the matrix has a “delayed” response to pressure changes that occur in the surrounding fractures. Such a non-concurrent response induces matrix-to. S. Gerami fracture cross-flow. 7

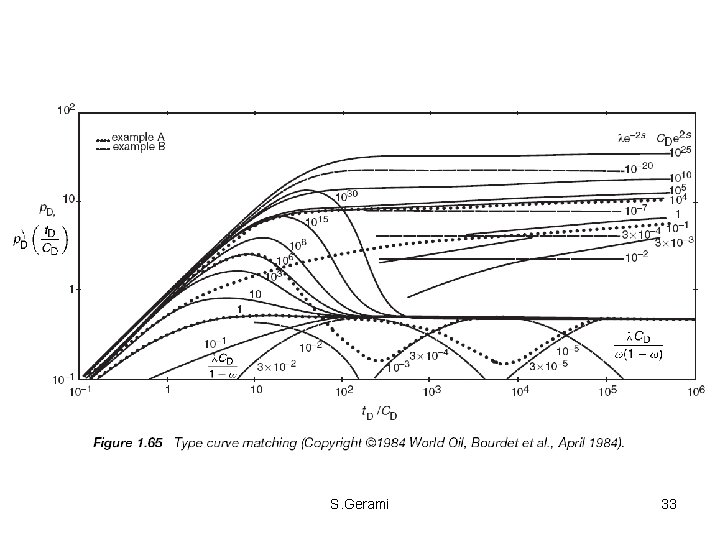
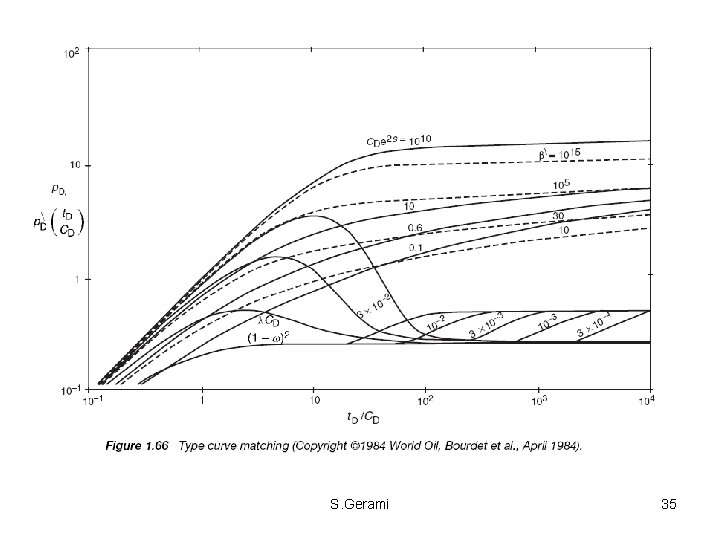
Characteristic of a Fractured Reservoir A typical double porosity response is characterized by two additional parameters, the inter-porosity flow parameter, λ, (representing a measure for the ease at which fluid is transferred from the matrix into the fractures), and storativity ratio, ω, (i. e. the ratio of fluid stored in the fracture system over the total stored fluid). The following two parameters are sufficient to characterize the deviation of a Fissured reservoir from that of homogeneous medium. Storativity ratio: A dimensionless parameter relating the fluid capacitance of the fracture porosity to that of combined flow. Interprosity flow parameter Typical values of λ range from 10 -3 to 10 -9, where low values of λ indicate low fluid transfer between matrix and fracture. For homogeneous reservoir S. Gerami 8

The factor α is the block-shape parameter that depends on the geometry and the characteristic shape of the matrix–fissures system and has the dimension of a reciprocal of the area. S. Gerami 9

S. Gerami 10

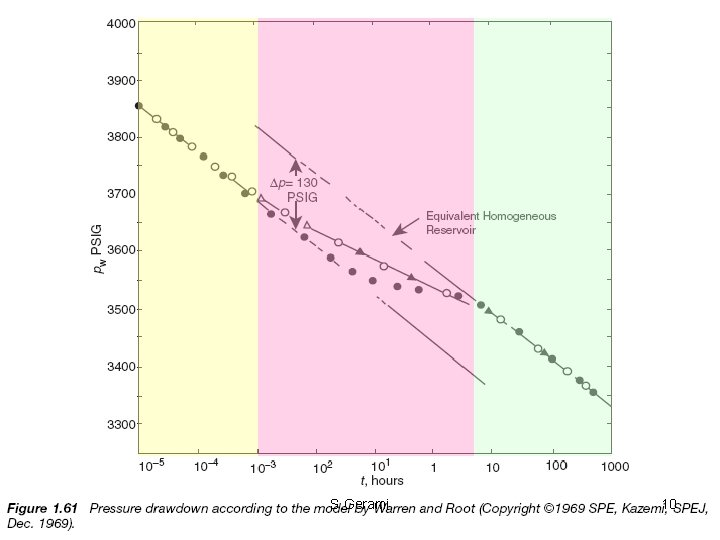
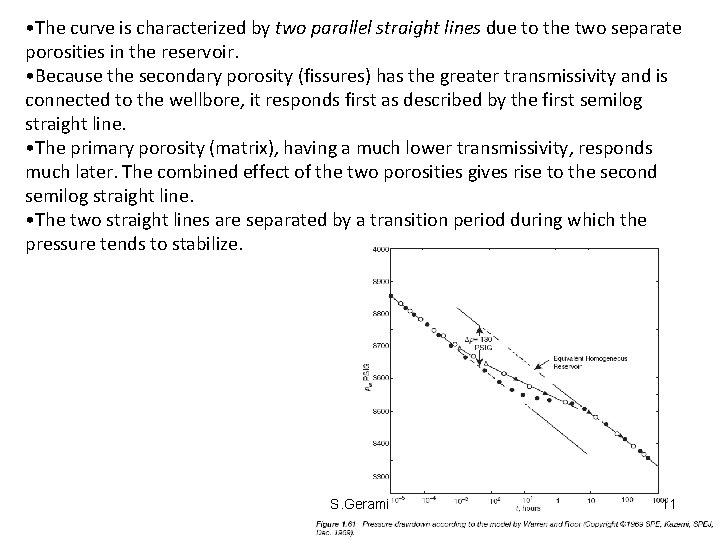
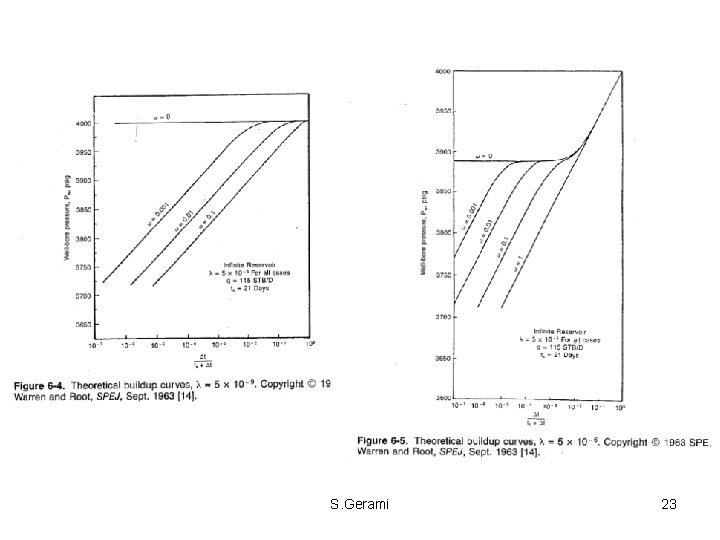
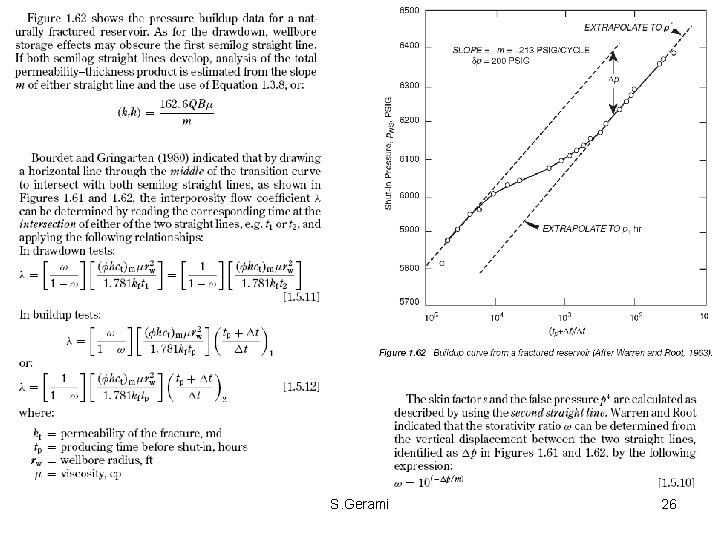
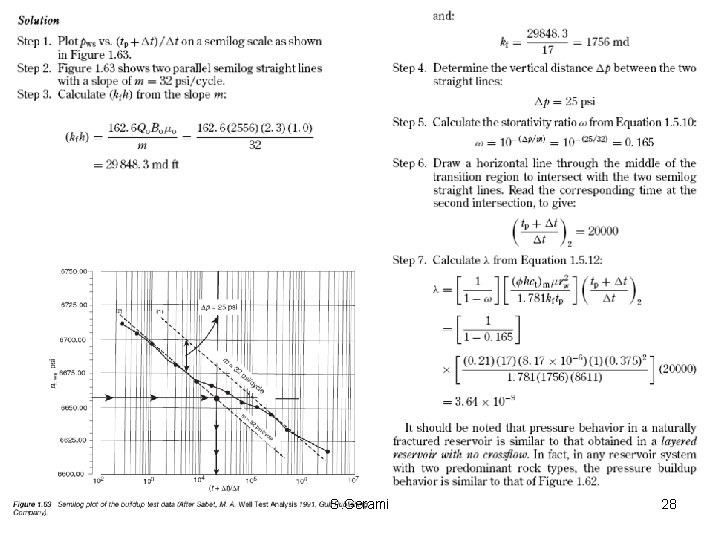
• The curve is characterized by two parallel straight lines due to the two separate porosities in the reservoir. • Because the secondary porosity (fissures) has the greater transmissivity and is connected to the wellbore, it responds first as described by the first semilog straight line. • The primary porosity (matrix), having a much lower transmissivity, responds much later. The combined effect of the two porosities gives rise to the second semilog straight line. • The two straight lines are separated by a transition period during which the pressure tends to stabilize. S. Gerami 11

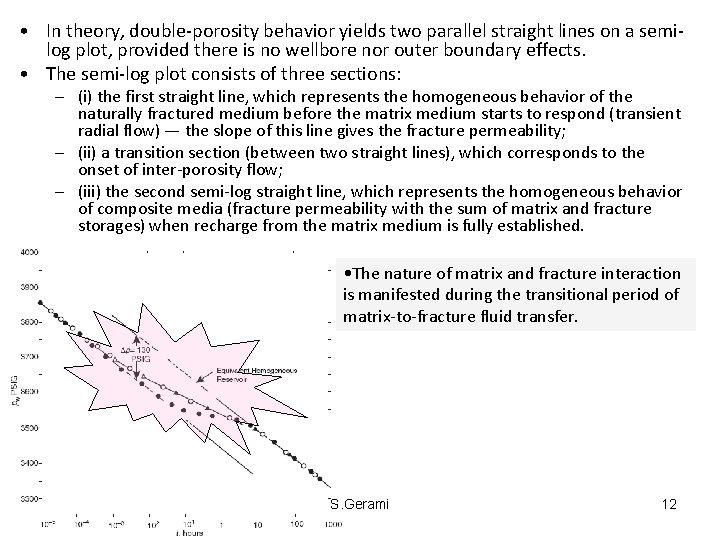
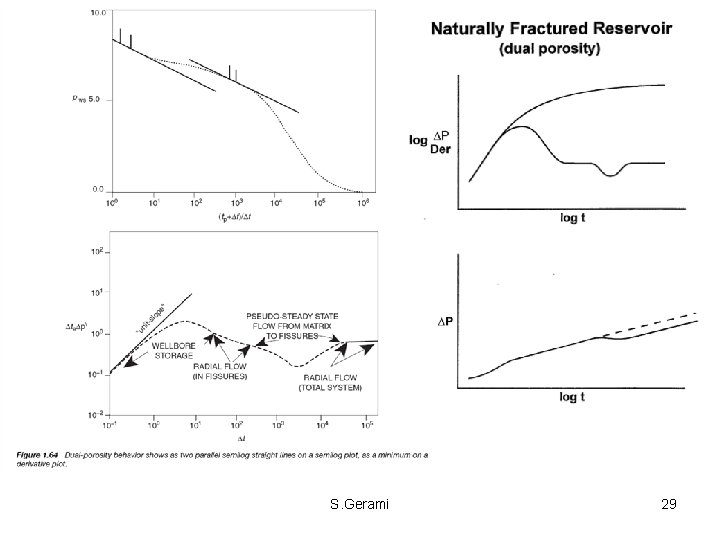
• In theory, double-porosity behavior yields two parallel straight lines on a semilog plot, provided there is no wellbore nor outer boundary effects. • The semi-log plot consists of three sections: – (i) the first straight line, which represents the homogeneous behavior of the naturally fractured medium before the matrix medium starts to respond (transient radial flow) — the slope of this line gives the fracture permeability; – (ii) a transition section (between two straight lines), which corresponds to the onset of inter-porosity flow; – (iii) the second semi-log straight line, which represents the homogeneous behavior of composite media (fracture permeability with the sum of matrix and fracture storages) when recharge from the matrix medium is fully established. • The nature of matrix and fracture interaction is manifested during the transitional period of matrix-to-fracture fluid transfer. S. Gerami 12

• • The characteristics of the transitional segment are determined by the way the matrix and fracture interact. Flow from matrix to fractures takes place according to the assumptions used in the available double porosity models: 1. 2. 3. The flow rate is proportional to the pressure difference between matrix and fracture (Warren and Root, 1963) The flow rate is proportional to the averaged pressure gradient through the matrix (Streltsova, 1983) The flow rate is an unsteady state function of pressure drop across the matrix(Kazemi, 1969; de. Swaan, 1976, and Najurrieta, 1980) S. Gerami 13

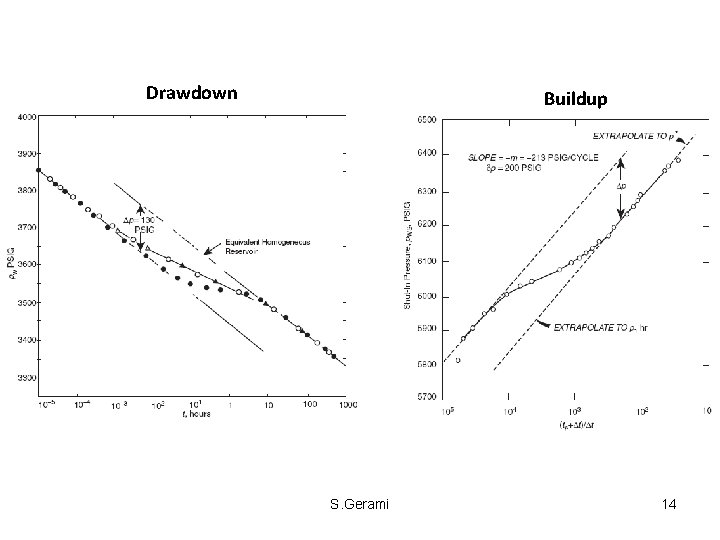
Drawdown Buildup S. Gerami 14

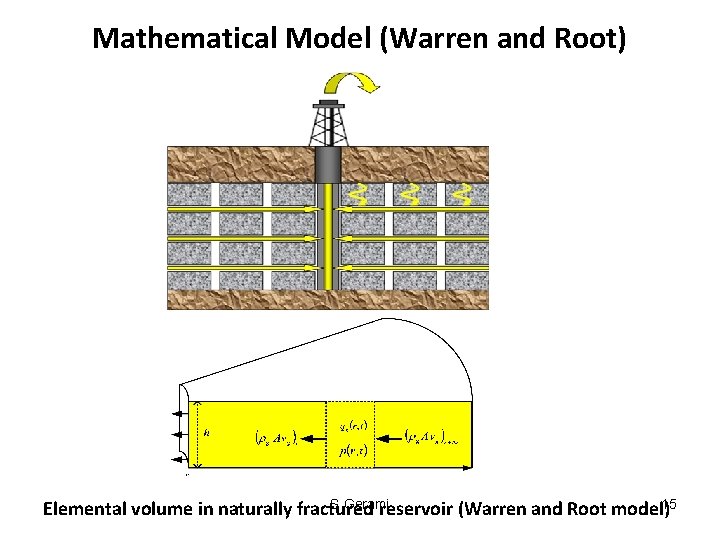
Mathematical Model (Warren and Root) S. Gerami Elemental volume in naturally fractured reservoir (Warren and Root model)15

S. Gerami 16

S. Gerami 17

S. Gerami 18

S. Gerami 19

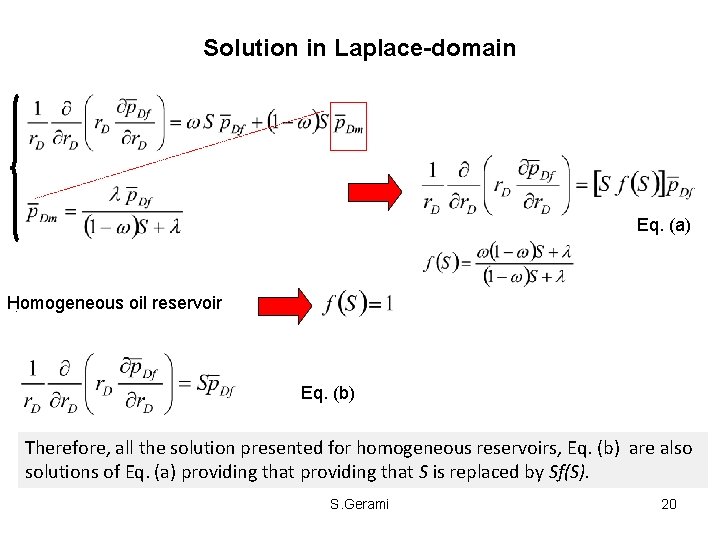
Solution in Laplace-domain Eq. (a) Homogeneous oil reservoir. Eq. (b) Therefore, all the solution presented for homogeneous reservoirs, Eq. (b) are also solutions of Eq. (a) providing that S is replaced by Sf(S). S. Gerami 20

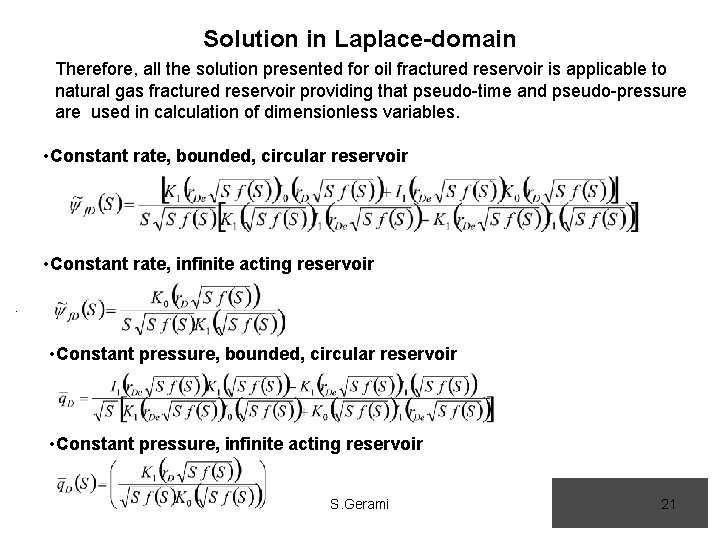
Solution in Laplace-domain Therefore, all the solution presented for oil fractured reservoir is applicable to natural gas fractured reservoir providing that pseudo-time and pseudo-pressure are used in calculation of dimensionless variables. • Constant rate, bounded, circular reservoir • Constant rate, infinite acting reservoir. • Constant pressure, bounded, circular reservoir • Constant pressure, infinite acting reservoir S. Gerami 21

S. Gerami 22

S. Gerami 23

Important Features of Some Mathematical Models Describing Flow from Matrix to Fracture Warren and Root (1965) Analytical model. Pseudo-steady state model. Matrix flux is independent of a spatial position and is proportional to the pressure difference between matrix and fracture. Simplifying the mathematical analysis of the flow problem. S-shaped transitional curve with an inflection point. The separation of the two parallel lines allows calculation of the storativity ratio. Kazemi (1969) Numerical model. Unsteady state model. Linear transitional curve with no inflection point. S. Gerami 24

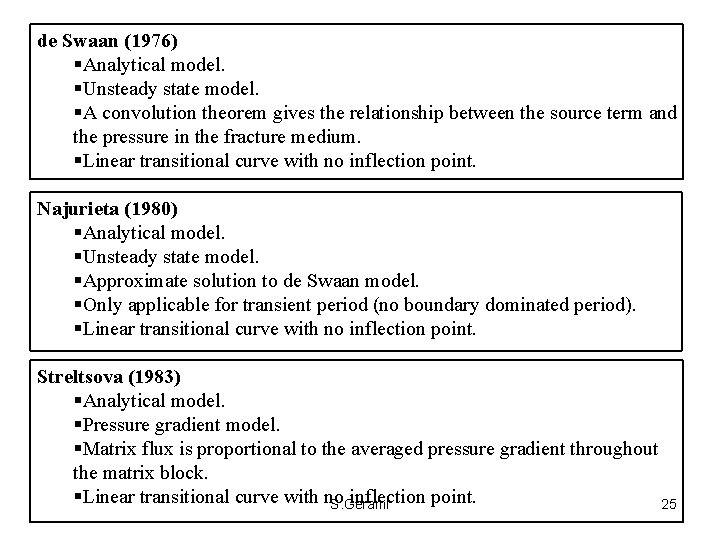
de Swaan (1976) Analytical model. Unsteady state model. A convolution theorem gives the relationship between the source term and the pressure in the fracture medium. Linear transitional curve with no inflection point. Najurieta (1980) Analytical model. Unsteady state model. Approximate solution to de Swaan model. Only applicable for transient period (no boundary dominated period). Linear transitional curve with no inflection point. Streltsova (1983) Analytical model. Pressure gradient model. Matrix flux is proportional to the averaged pressure gradient throughout the matrix block. Linear transitional curve with no inflection point. S. Gerami 25

S. Gerami 26

S. Gerami 27

S. Gerami 28

S. Gerami 29

S. Gerami 30

Drawdown Buildup S. Gerami 31

S. Gerami 32

S. Gerami 33

S. Gerami 34

S. Gerami 35

S. Gerami 36

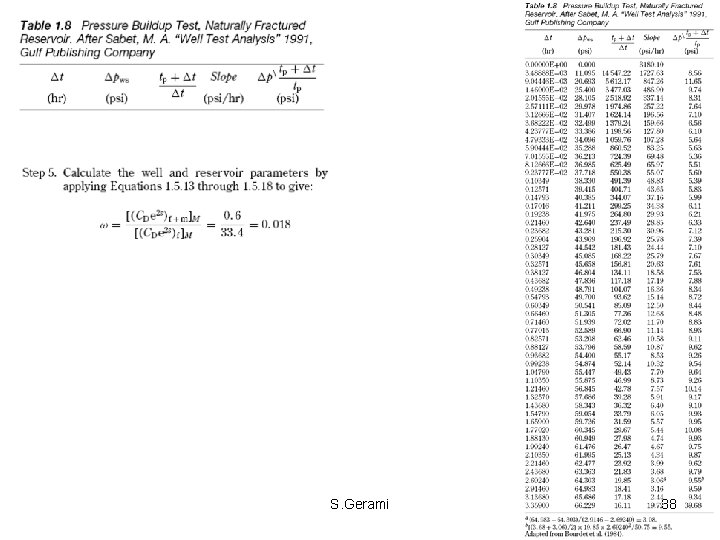
S. Gerami 37

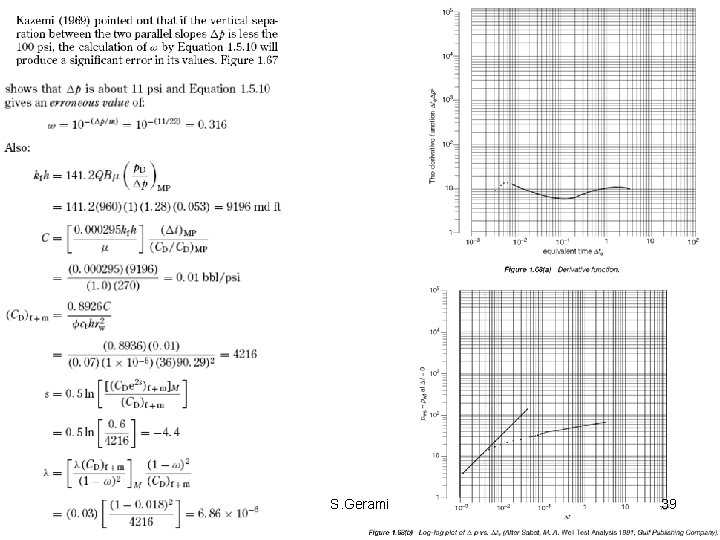
S. Gerami 38

S. Gerami 39

S. Gerami 40

Identification Of Double Porosity System from Well Tests In practice the two parallel straight line may or may not be present ( It depends on the condition of the well, composition of the reservoir fluid, duration of the test, …) thus a semilog plot is not an efficient tool for identifying double porosity behavior. ¯ Double porosity behavior yields an S-shaped log-log pressure curve on a loglog plot. ¯ Double porosity behavior is characterized by the existence of a minimum on the pressure derivative. ¯ The P. S. S. model shows a V-shaped minimum ¯ The Transient models show an open U-shaped minimum. ¯ S. Gerami 41