Well Testing Module 2 Fundamentals of fluid flow

Well Testing Module #2: Fundamentals of fluid flow in porous media Shahab Gerami, Ph. D 1 S. Gerami

Outline • 1 -D unsteady state flow of a slightly compressible through a homogeneous porous media • Development of Hydraulic Diffusivity Equation for Flow of a Slightly Compressible Oil • Solution • Applications 2 S. Gerami

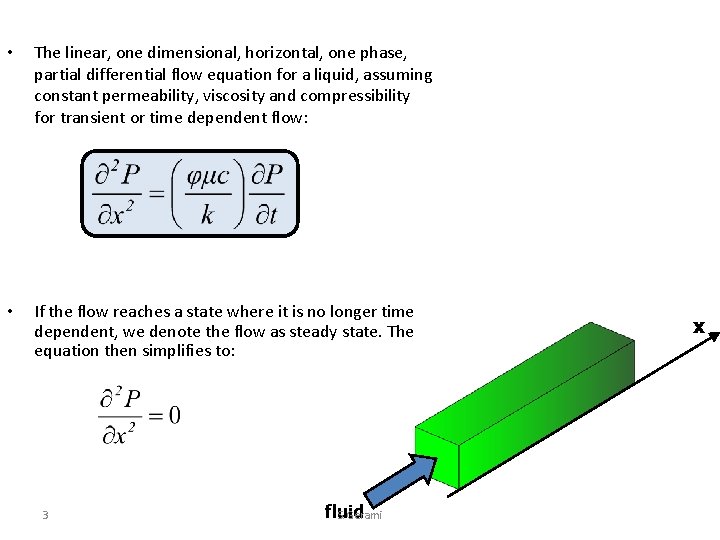
• The linear, one dimensional, horizontal, one phase, partial differential flow equation for a liquid, assuming constant permeability, viscosity and compressibility for transient or time dependent flow: • If the flow reaches a state where it is no longer time dependent, we denote the flow as steady state. The equation then simplifies to: 3 fluid S. Gerami x

• Transient and steady state pressure distributions are illustrated graphically in the figure below for a system where initial and right hand pressures are equal: Left side pressure Steady state solution Transient solution Initial and right side pressure 4 S. Gerami

Development of Hydraulic Diffusivity Equation for Flow of a Slightly Compressible Oil and Its Solution Subjected to Different Boundary Conditions • • • – – Physical model Simplifying assumptions Mathematical model Choosing an appropriate element Governing equation • Mass balance • Momentum balance (Darcy’s law) • Equation of state Initial and Boundary conditions • Infinite acting – Constant rate production – Constant pressure production • Finite acting – Constant rate production – Constant pressure production Solutions • • 5 Laplace space solutions Time domain solutions Simplified solutions Applications (Drawdown (single rate & multi rate), Reservoir limit test, Build up, Superposition (time & space), …), S. Gerami

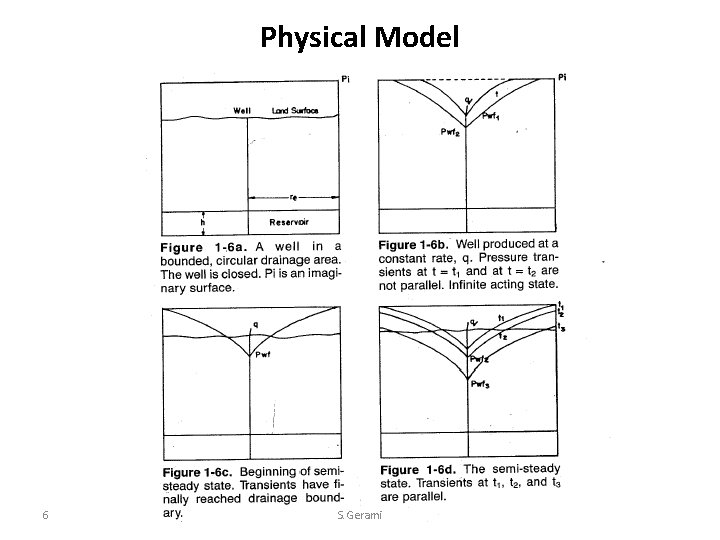
Physical Model 6 S. Gerami

Simplifying Assumptions 7 S. Gerami

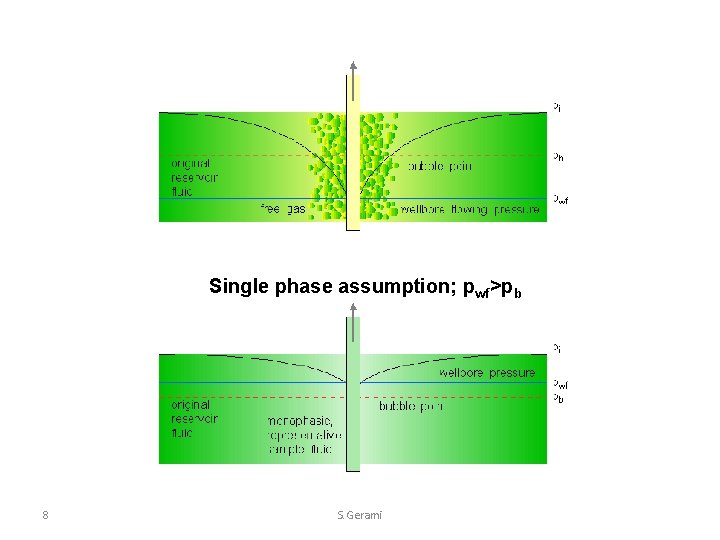
Single phase assumption; pwf>pb 8 S. Gerami

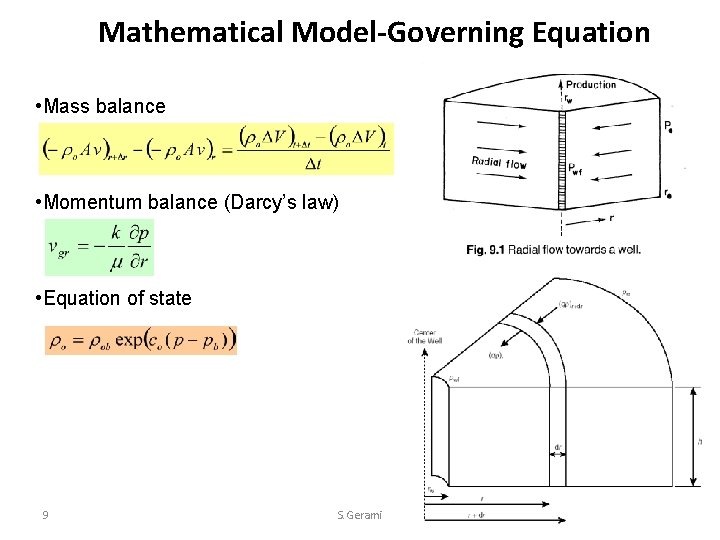
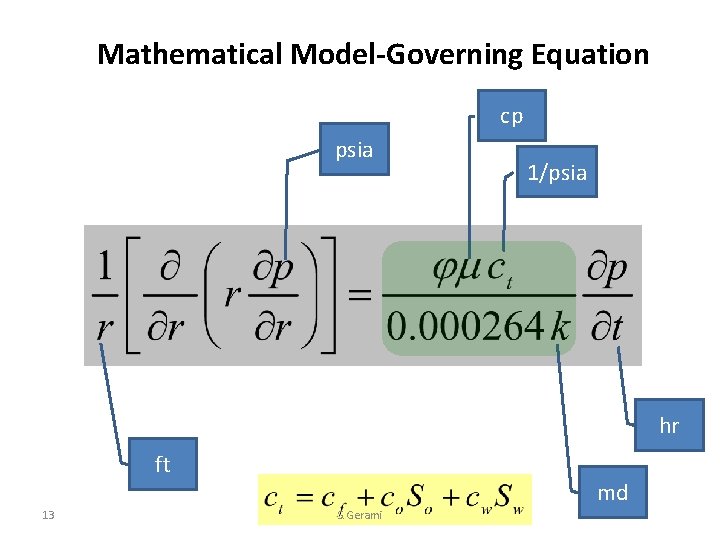
Mathematical Model-Governing Equation • Mass balance • Momentum balance (Darcy’s law) • Equation of state 9 S. Gerami

10 S. Gerami

11 S. Gerami

12 S. Gerami

Mathematical Model-Governing Equation cp psia 1/psia hr ft 13 md S. Gerami

Hydraulic Diffusivity Equation Hydraulic diffusivity equation determines the velocity at which pressure waves propagate in the reservoir. The more the permeability the faster the pressure wave will propagate. 14 S. Gerami

Dimensionless Variables 15 S. Gerami

16 S. Gerami

Dimensionless Hydraulic Diffusivity Equation 17 S. Gerami

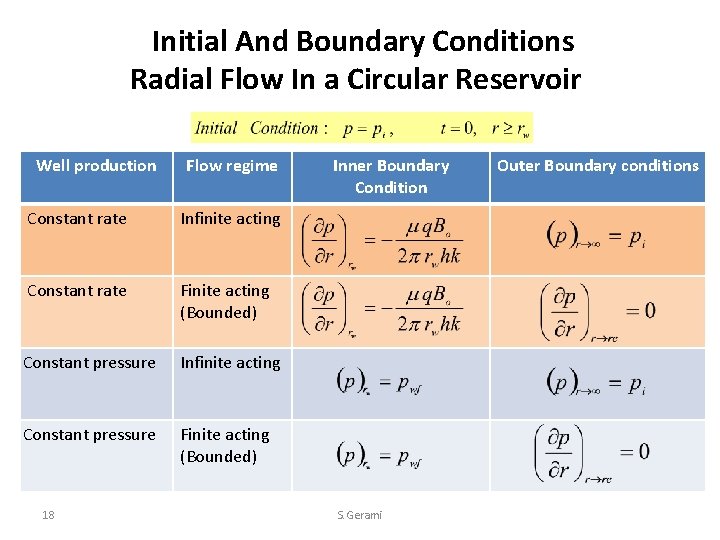
Initial And Boundary Conditions Radial Flow In a Circular Reservoir Well production Flow regime Constant rate Infinite acting Constant rate Finite acting (Bounded) Constant pressure Infinite acting Constant pressure Finite acting (Bounded) 18 Inner Boundary Condition S. Gerami Outer Boundary conditions

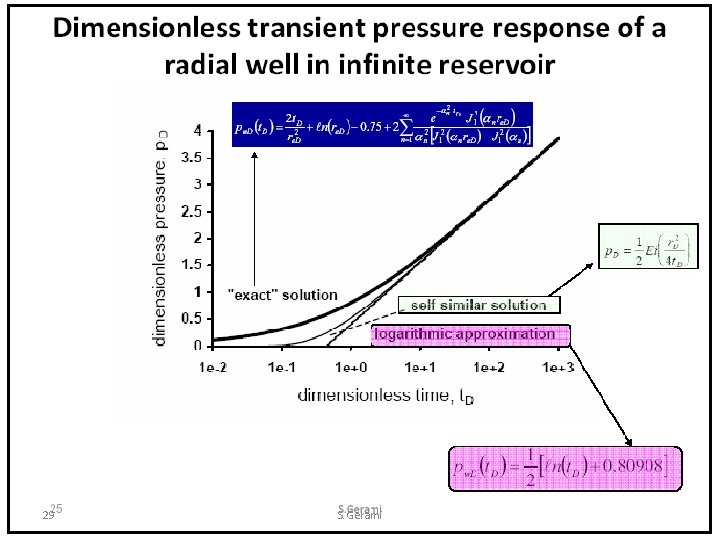
van Everdingen- Hurst Constant Terminal Rate Solution Bounded Cylindrical Reservoir (exact solution) Approximate Solutions 1. Infinite cylindrical reservoir with line-source well 2. Bounded cylindrical reservoir, pseudo steady-state flow 19 S. Gerami

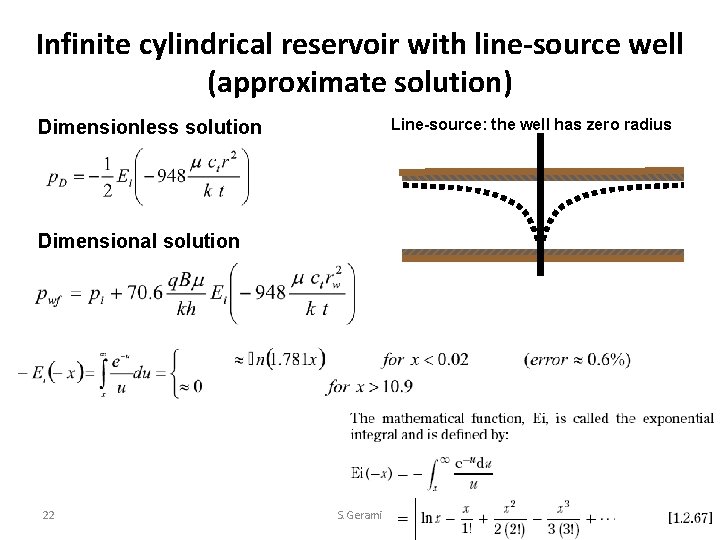
wellbore Solutions-source & Finite-Line • The solution to differential equations treating the well as a vertical line through a porous medium. The solution is nearly identical to the finitewellbore solution. At very early times, there is a notable difference in the solutions, but the differences disappear soon after a typical well is opened to flow or shut in for a buildup test, and in practice the differences are masked by wellbore storage. • The solution to the diffusivity equation that results when the well (inner) boundary condition is treated as a cylinder of finite radius instead of treating the well as a line source. Line-source: the well has zero radius 20 wellbore-Finite S. Gerami

21 S. Gerami

Infinite cylindrical reservoir with line-source well (approximate solution) Line-source: the well has zero radius Dimensionless solution Dimensional solution 22 S. Gerami

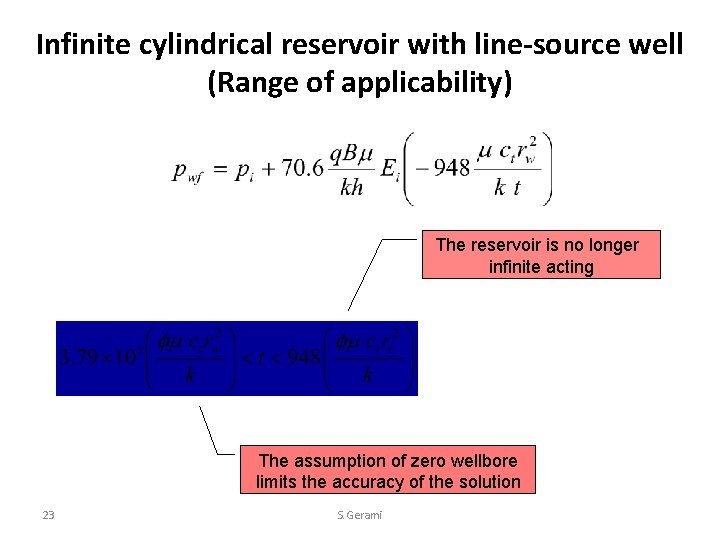
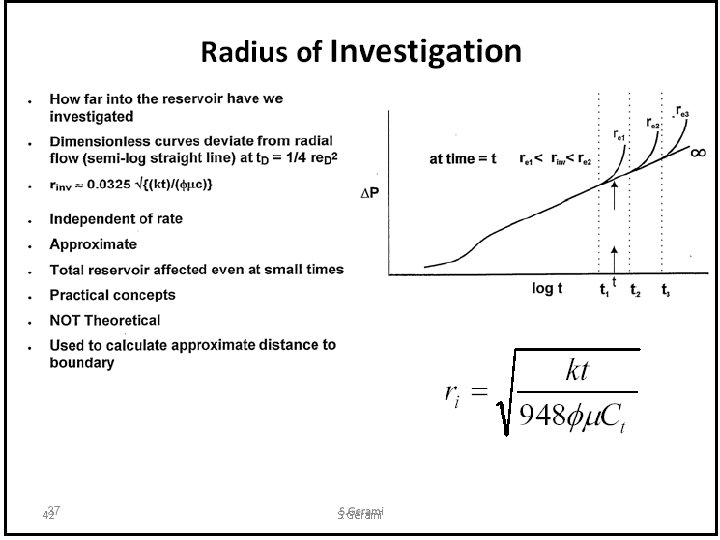
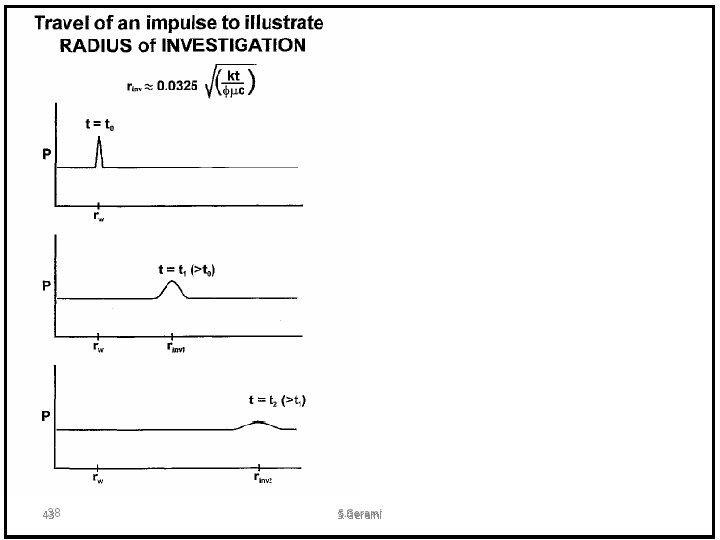
Infinite cylindrical reservoir with line-source well (Range of applicability) The reservoir is no longer infinite acting The assumption of zero wellbore limits the accuracy of the solution 23 S. Gerami

Example • 24 A well is producing only oil at constant rate of 20 STB/D. Data describing the well and formation are summarized below. Calculate the reservoir pressure at radii of 1, 10, and 100 ft after 3 hrs of production. S. Gerami

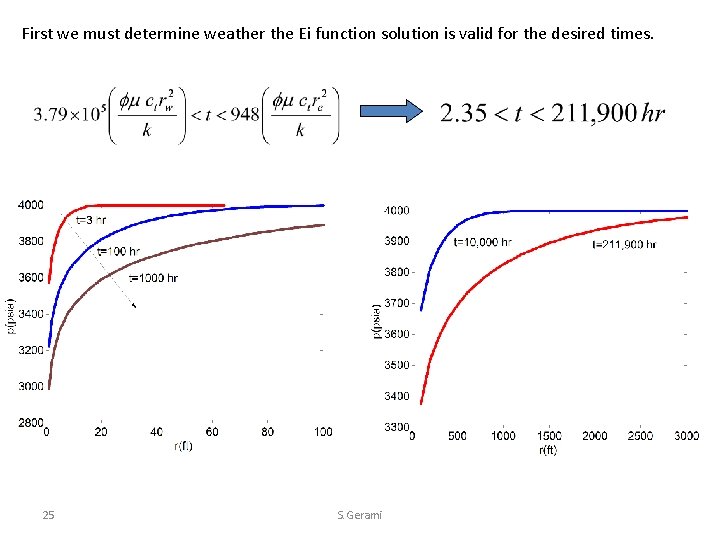
First we must determine weather the Ei function solution is valid for the desired times. 25 S. Gerami

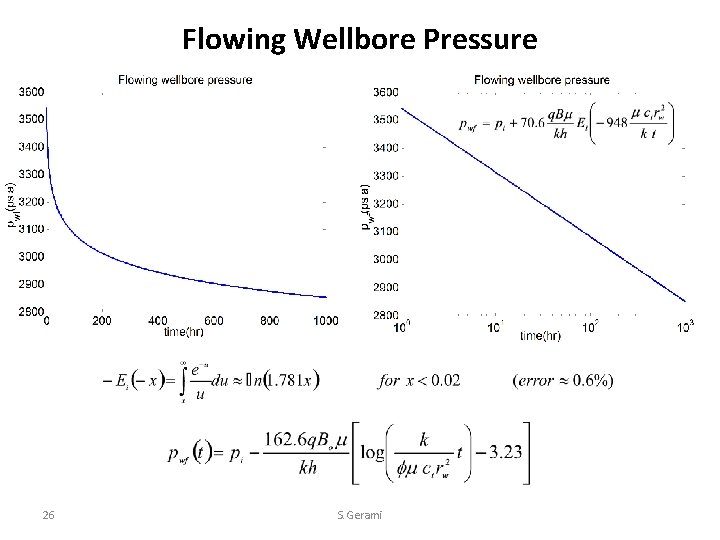
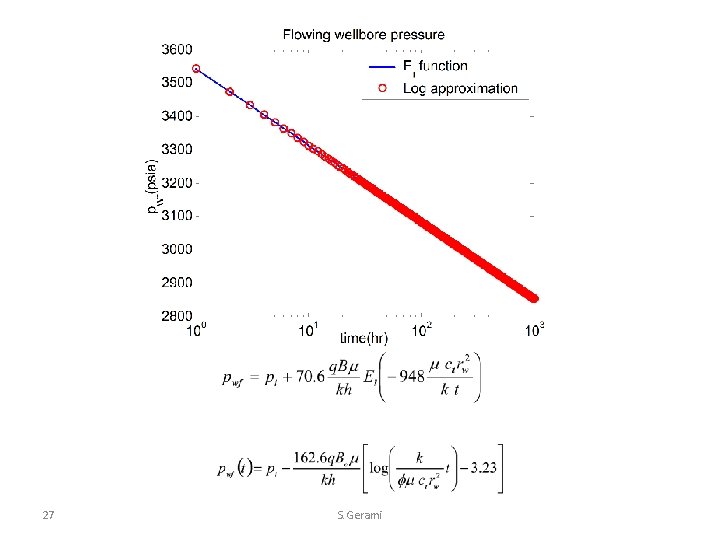
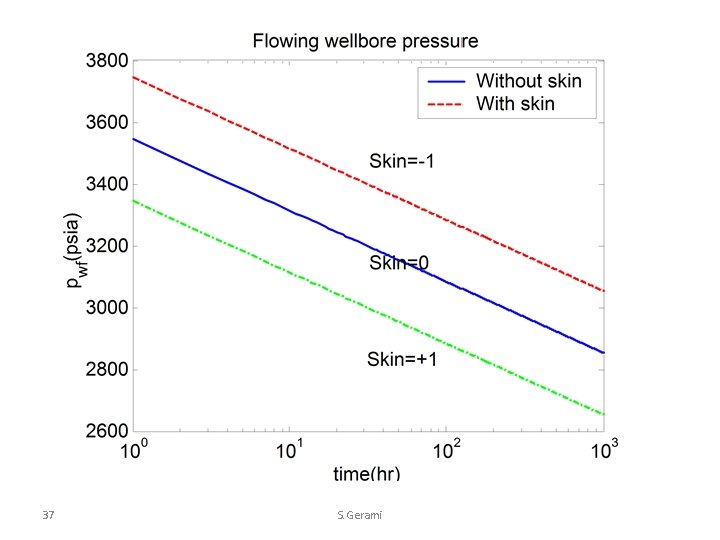
Flowing Wellbore Pressure 26 S. Gerami

27 S. Gerami

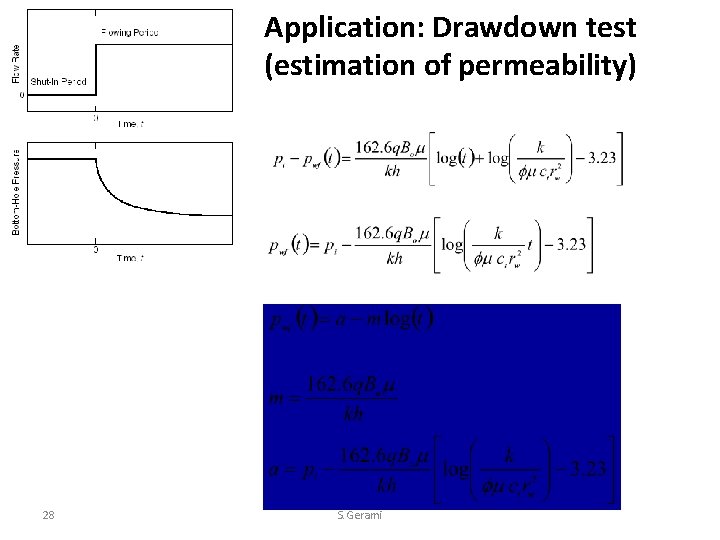
Application: Drawdown test (estimation of permeability) 28 S. Gerami

29 S. Gerami

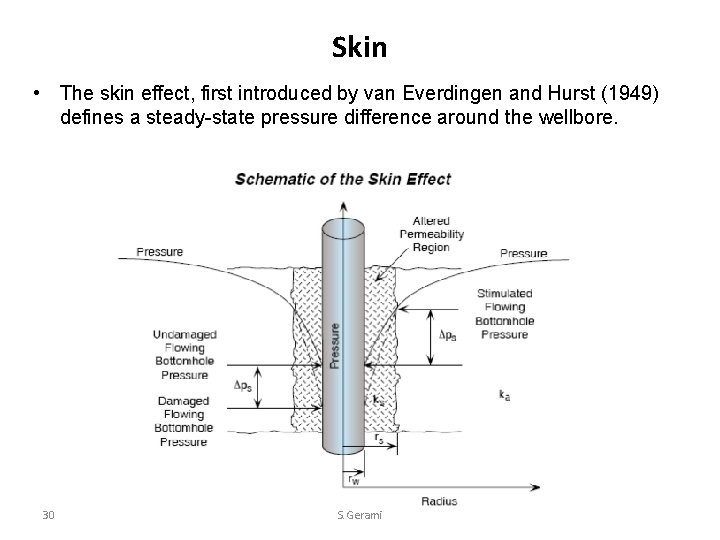
Skin • The skin effect, first introduced by van Everdingen and Hurst (1949) defines a steady-state pressure difference around the wellbore. 30 S. Gerami

Skin • Skin zone: The region of altered permeability (A few inches to several feet from the wellbore). The effect of the skin zone is to alter the pressure distribution around the wellbore. • Wellbore damage : reduction of the permeability around the wellbore due to entrance of materials such as mud filtrate, cement slurry, or clay particles during drilling, completion, or workover operations. • Wellbore stimulation : increasing of the permeability near the wellbore using: • Acidizing • Fracturing 31 S. Gerami • In case of wellbore damage, the skin zone causes an additional pressure loss in the formation. • In case of wellbore improvement, the opposite to that of wellbore damage occurs.

Skin Development Skin, S, refers to a region near the wellbore of improved or reduced permeability compared to the bulk formation permeability. Impairment (+S): • Overbalanced drilling (filtrate loss) • Perforating damage • Unfiltered completion fluid • Fines migration after long term production • Non-darcy flow (predominantly gas well) • Condensate banking- acts like turbulence Stimulation (-S) • Frac pack (0 to -0. 5) • Acidizing • Hydraulic fracturing Generally S>5 is considered bad; S= -3. 5 to -4 is excellent. 32 S. Gerami

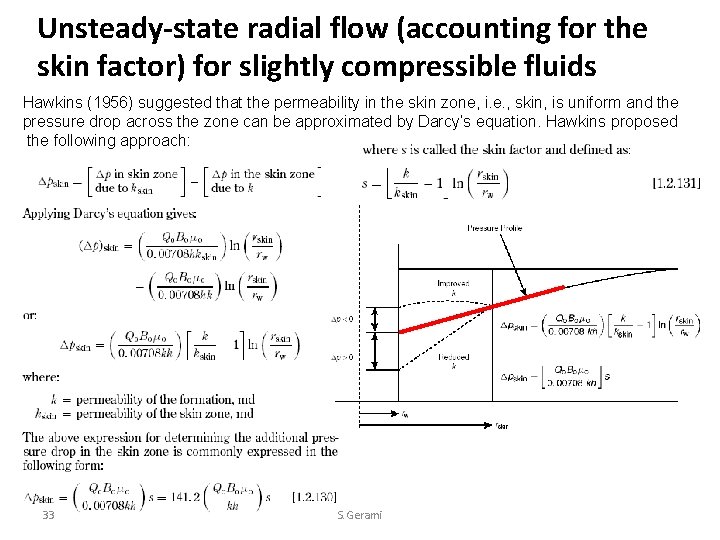
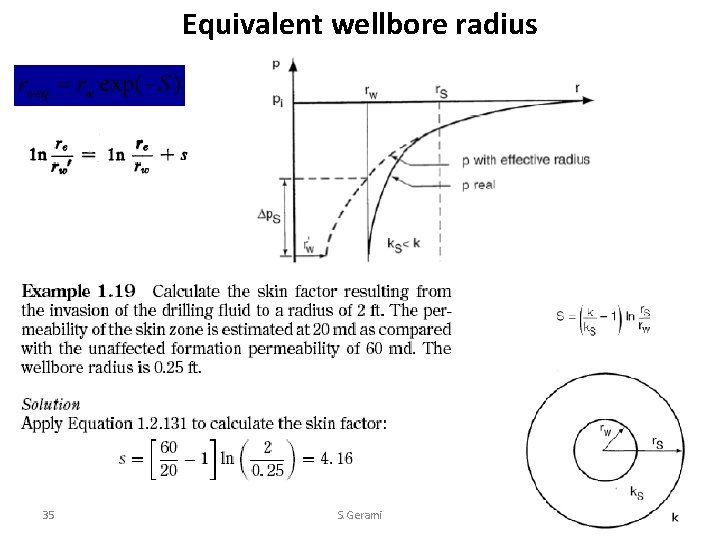
Unsteady-state radial flow (accounting for the skin factor) for slightly compressible fluids Hawkins (1956) suggested that the permeability in the skin zone, i. e. , skin, is uniform and the pressure drop across the zone can be approximated by Darcy’s equation. Hawkins proposed the following approach: 33 S. Gerami

34 S. Gerami

Equivalent wellbore radius 35 S. Gerami

Application: Accounting for Skin 36 S. Gerami

37 S. Gerami

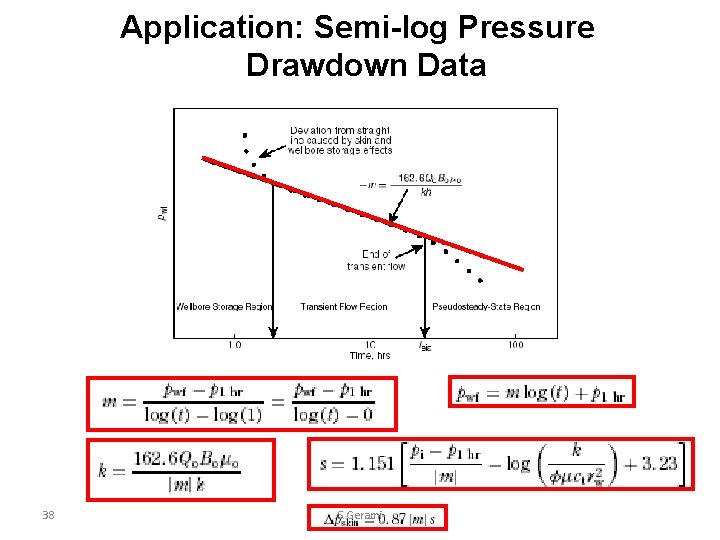
Application: Semi-log Pressure Drawdown Data 38 S. Gerami

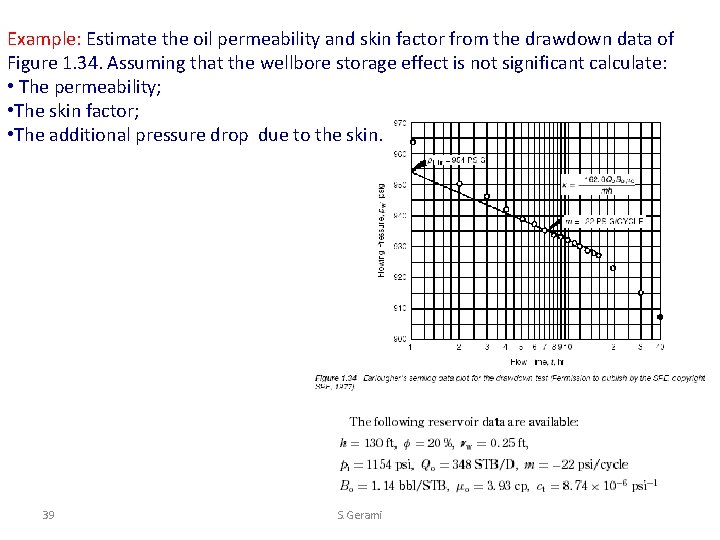
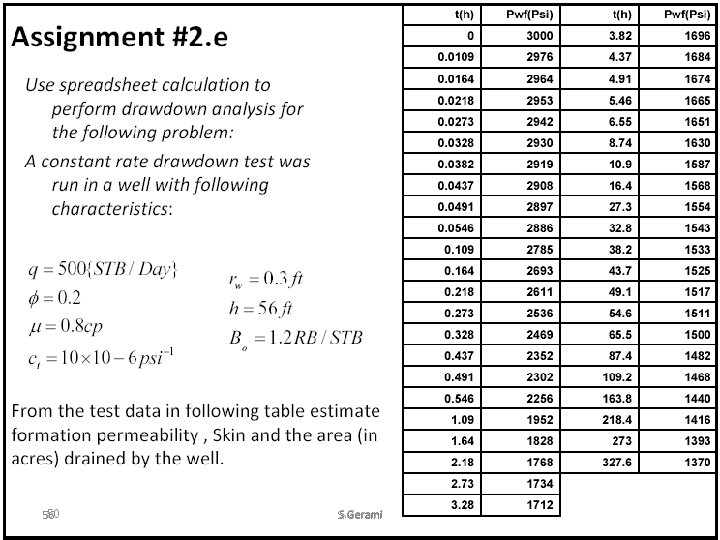
Example: Estimate the oil permeability and skin factor from the drawdown data of Figure 1. 34. Assuming that the wellbore storage effect is not significant calculate: • The permeability; • The skin factor; • The additional pressure drop due to the skin. 39 S. Gerami

Solution Step 1. From Figure 1. 34, calculate p 1 hr: p 1 hr = 954 psi Step 2. Determine the slope of the transient flow line: m = -22 psi/cycle Step 3. Calculate the permeability: Step 4. Solve for the skin factor s Step 5. Calculate the additional pressure drop: 40 40 S. Gerami

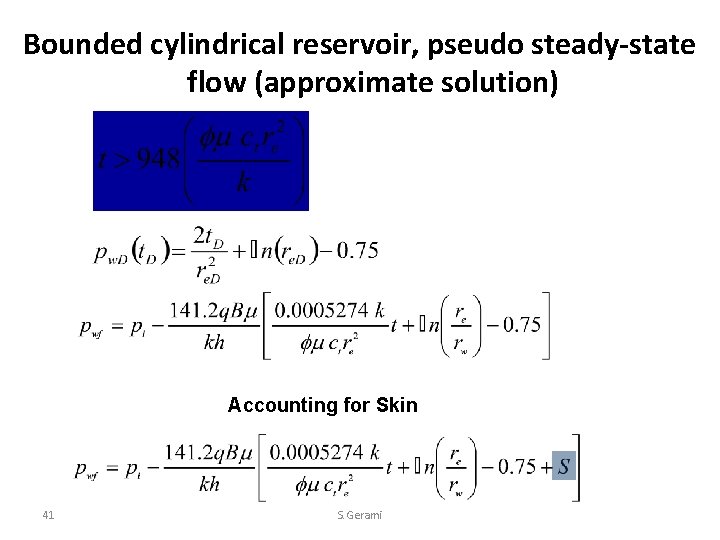
Bounded cylindrical reservoir, pseudo steady-state flow (approximate solution) Accounting for Skin 41 S. Gerami

42 S. Gerami

43 S. Gerami

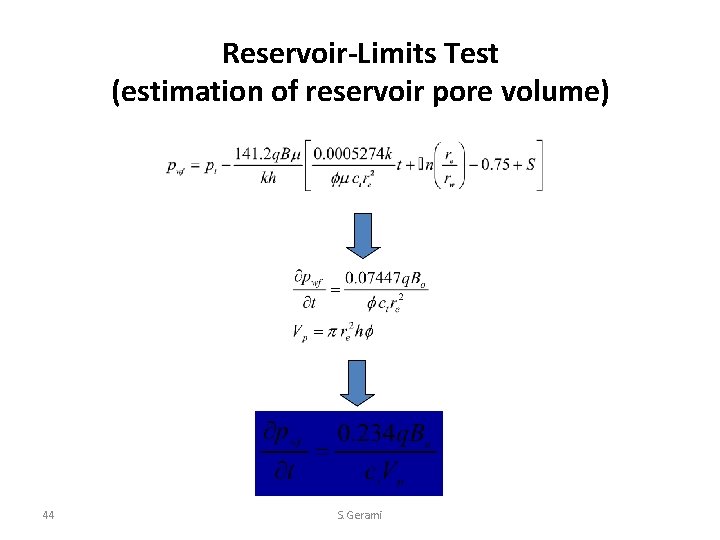
Reservoir-Limits Test (estimation of reservoir pore volume) 44 S. Gerami

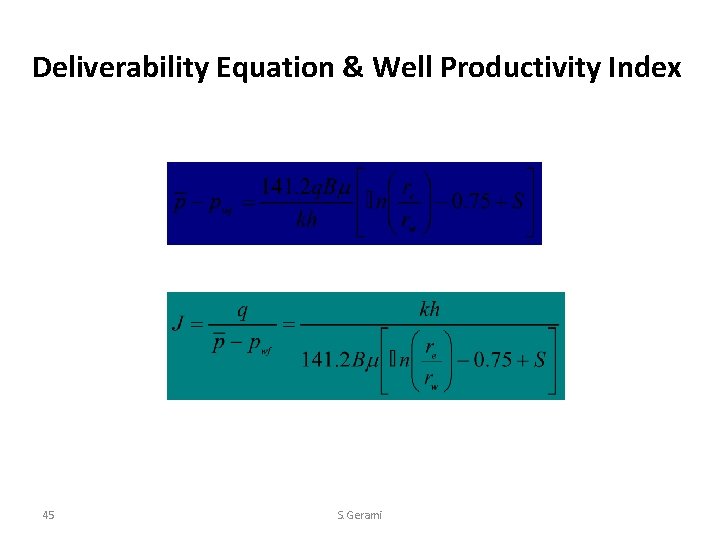
Deliverability Equation & Well Productivity Index 45 S. Gerami

46 S. Gerami

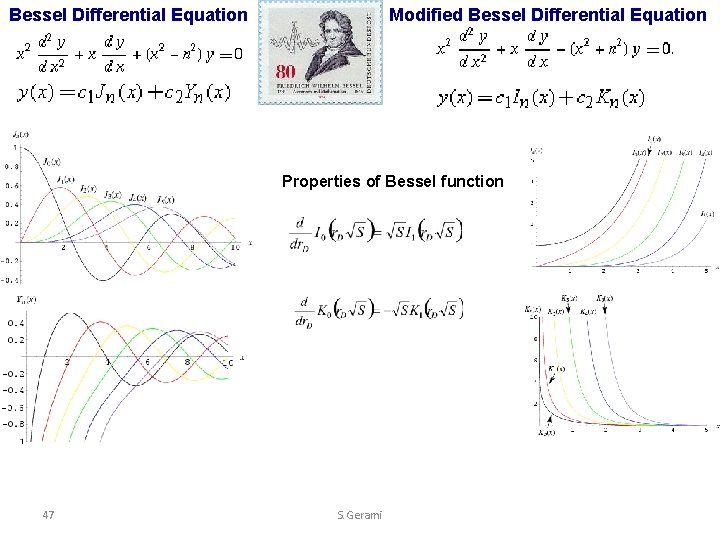
Bessel Differential Equation Modified Bessel Differential Equation Properties of Bessel function 47 S. Gerami

Solutions- Laplace Domain (Sabet, 1991). Infinite-acting reservoir Constant rate solution Bounded reservoir Infinite-acting reservoir Constant pressure solution 48 Bounded reservoir S. Gerami

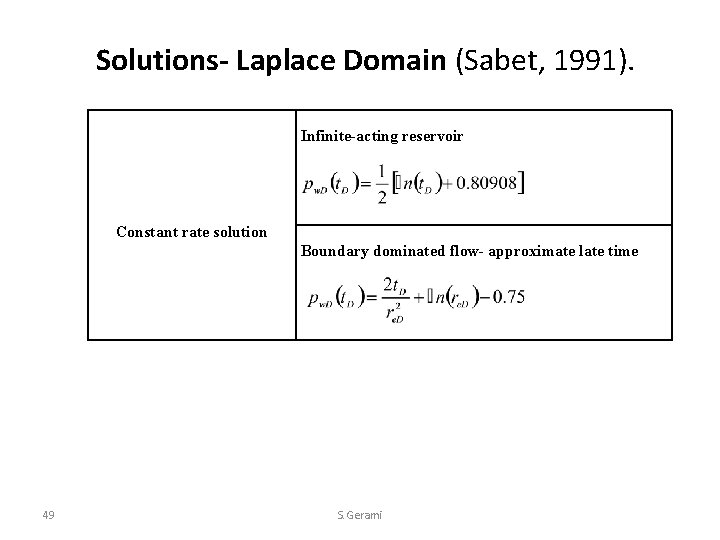
Solutions- Laplace Domain (Sabet, 1991). Infinite-acting reservoir Constant rate solution Boundary dominated flow- approximate late time 49 S. Gerami

Numerical Inverse Laplace Transformation 50 S. Gerami

Numerical Inverse Laplace Transformation (Stehfest Algorithm) 51 S. Gerami

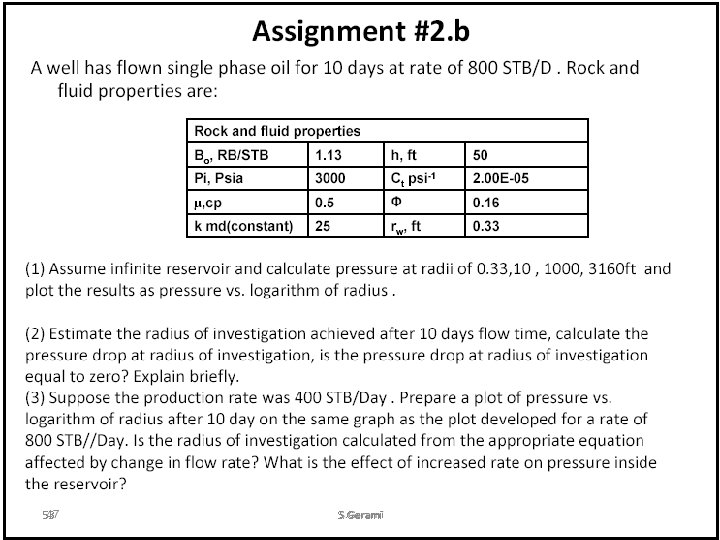
Assignment #2. a An oil well is producing at a constant flow rate of 500 STB/day under unsteady-state flow conditions. The reservoir has the following rock and fluid properties: (1) Calculate the pressure at radii of 0. 3, 5, 10, 50, 100, 500, 1000, 1500, 2000, and 2500 ft, for 1 hour. Plot the results as: (a) pressure versus the logarithm of radius; (b) pressure versus radius (2) Repeat part 1 for t = 12 hours and 24 hours. Plot the results as pressure versus logarithm of radius. (3) Estimate the bottom-hole flowing pressure after 10 hours of production. 52 S. Gerami

53 S. Gerami

54 S. Gerami

55 S. Gerami

56 S. Gerami