Welcome to the Wonderful World of Expectations represent














































- Slides: 53

Welcome to the Wonderful World of ….

Expectations - represent, compare, and order whole numbers to 1 000. – demonstrate an understanding of place value in whole numbers from 0. 001 to 1 000. – read and print in words whole numbers to one hundred thousand.

Vocabulary To Know Numeral Digit Place Value Face Value Zero Place Holder Value Periods Scientific Notation Expanded Form Written Form Standard Form

Digits and Numerals: A symbol or name that stands for a number. Numerals = Numbers (synonymns) Examples: 3, 49 and twelve are all numerals Digits: A symbol used to make numerals. 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 are the ten digits we use in everyday numbers. Example: the numeral 153 is made up of 3 digits ("1", "5" and "3").

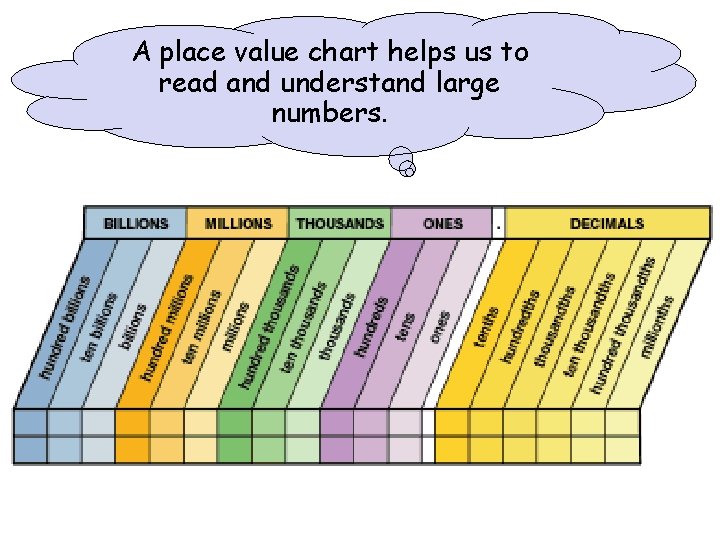
Place Value is the value of a digit determined by its position in a number. A place value chart helps us to read and understand large numbers.

Try this • In each one of your bags, you have the following place value names. Can you put them in order from smallest to largest? tens thousands hundred millions ten thousands hundred thousands ten millions ones billions

Answers Smallest to Largest » Ones » Tens » Hundreds » Thousands » ten thousand » Hundred thousand » Millions » Ten millions » Hundred millions » Billions Did you get them all right? Great Work!

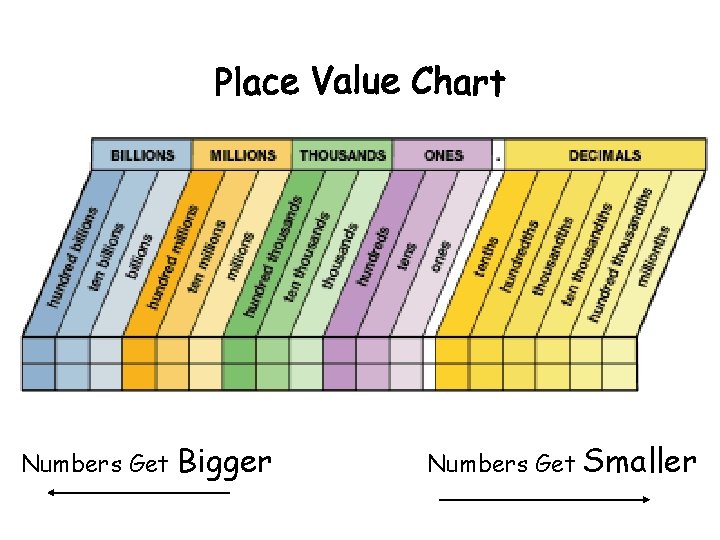
A place value chart helps us to read and understand large numbers.

Numbers Get Bigger Numbers Get Smaller

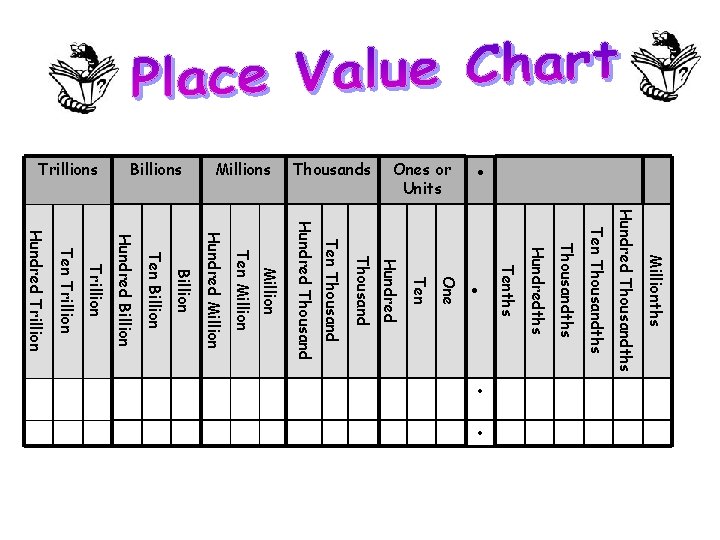
• Ones or Units Thousands Millions Billions Trillions Millionths Hundred Thousandths Ten Thousandths Hundredths • Tenths • One Ten Hundred Thousand Ten Thousand Hundred Thousand Million Ten Million Hundred Million Billion Ten Billion Hundred Billion Trillion Ten Trillion Hundred Trillion •

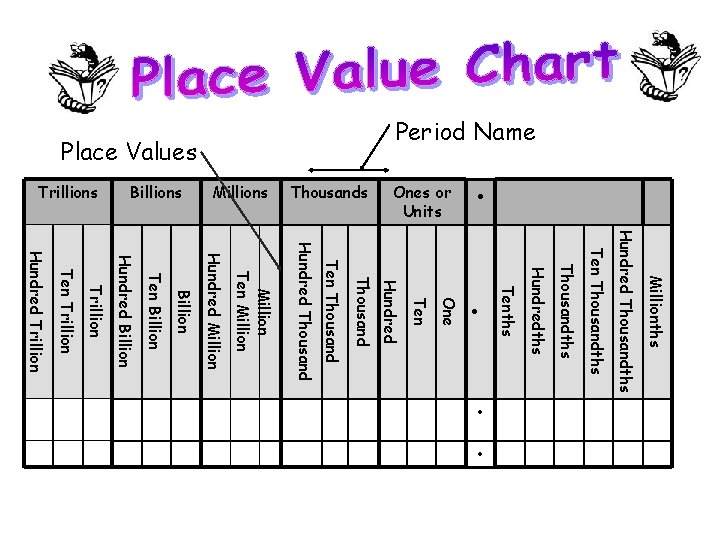
Place Values • Ones or Units Thousands Millions Billions Trillions Period Name Millionths Hundred Thousandths Ten Thousandths Hundredths • Tenths • One Ten Hundred Thousand Ten Thousand Hundred Thousand Million Ten Million Hundred Million Billion Ten Billion Hundred Billion Trillion Ten Trillion Hundred Trillion •

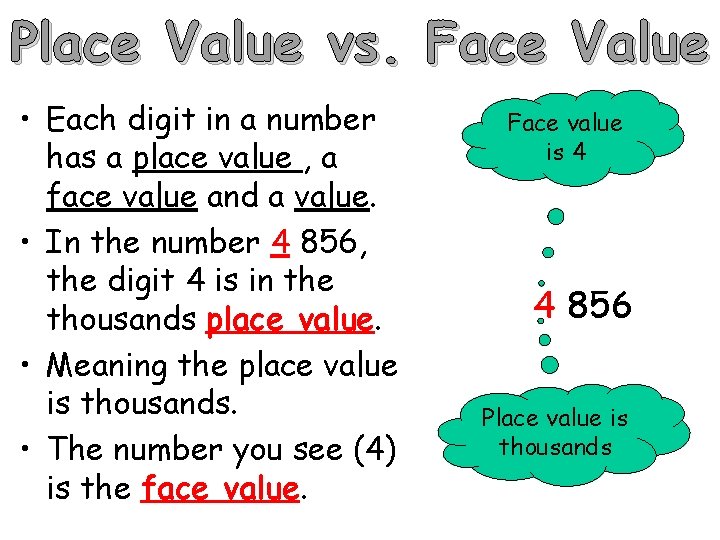
Place Value vs. Face Value • Each digit in a number has a place value , a face value and a value. • In the number 4 856, the digit 4 is in the thousands place value. • Meaning the place value is thousands. • The number you see (4) is the face value. Face value is 4 4 856 Place value is thousands

Practice What is the place value of the six (6) in each of the following numbers? Place Value (? ) a) 16 978 thousands b) 45 678 090 hundred thousands c) 69 218 d) 1 769 e) 92 628 f) 978 856 g) 6 876 432 ten thousands tens hundreds ones millions

Practice a. What is the face value of the digit in the hundreds place in each of the following numbers? Face Value (? ) a) 16 978 b) 45 678 090 c) 69 218 d) 1 769 e) 92 628 f) 978 856 g) 6 876 432 9 0 2 7 6 8 4

Value The value of a place is how much the digit in that place is worth. Example: What is the value of the digit four (4) in each number? a) 456 a) 400 b) 45 678 b) 40 000 c) 567 894 c) 4 d) 99 040 d) 40

Practice a. What is the place value of the nine (9) in each of the following numbers? b. What is the value of the nine (9) in each of the following numbers Value (? ) Place Value (? ) 900 a) 12 978 hundreds 90 b) 45 678 090 tens 9 000 thousands c) 79 018 d) 1 009 e) 92 128 f) 978 085 g) 9 876 432 ones ten thousands hundred thousands millions 9 90 000 900 000 9 000

Zero: The Hero • Zero is used as a place holder to show there is a place value, but there is no value to that place. • Zeros are put in to the right of numbers Example: 40 556 Zero is the place holder for the thousands place because there is no value for it, but we still need to show that there is a place for the thousands



• Numbers are grouped in sets of three called a period. • Each period has three places: the ones, tens and hundreds.

Periods THOUSANDS BILLIONS 128 063 245 791 MILLIONS UNITS ones, tens, hundreds

Example 4, 658, 089 Millions period Thousands period Ones period Four million, six hundred fifty-eight thousand, eighty-nine.

Millions Thousands 9 Thousandths 8 Hundredths 6 Tenths 7 One 3 Ten 5 Hundred 1 Thousand 2 Ten Thousand Hundred Thousand Millions Ten Million Hundred Million 1 Ones or Units 1. Read the entire number in each period, then add the period name to the end e. g. “One hundred twenty one” million “Five hundred thirty seven” thousand “Six hundred eighty nine” One hundred twenty one million, five hundred thirty seven thousand, six hundred eighty nine. ***Notice no AND was used to read whole numbers***

34 907 521 When saying large numbers you should: A) start with the largest place value grouping (period) on the left hand side. 34 907 521 B) Say the number, then say the grouped place value period “Thirty four” + million = “Thirty four million”

C) Move to right and say the number in the next period. 34 907 521 “Nine hundred seven” + thousand = “Nine hundred seven thousand” D) Keep moving right and say the number in the next period. 34 907 521 “Five hundred twenty one” + hundreds = “Five hundred twenty one” *** the period name for the hundreds can be dropped when saying or writing the number. ***

34 907 521 Now you can add all the names together. “Thirty-four million nine hundred seven five hundred twenty-one” ALERT “AND” is only said or written when there is a decimal. DO NOT say “and” if there isn’t a decimal. ( It’s hard, but you can do it!)

Example #1 12 001 1. 2. 3. 4. Say the number in the left period first. Next, add the period name to the end of it. Then say the number in the period to its right. We can leave the family name hundreds off. 12 001 = Twelve thousand one Remember No “and” is used, since we are not using decimals yet.

Example #2 1 000 562 When there is no value in one family, you do not have to include saying that family when writing the number. 1 000 562 = one million five hundred sixty two Notice we did not include thousands period. We did not have to include zero thousands

546 8 601 12 897 000 77 1 000 004 600 13 050 155 954 523 3 010 Five hundred forty six Eight thousand six hundred one Twelve million eight hundred ninety seven thousand Seventy seven One billion four thousand six hundred Thirteen thousand fifty One hundred fifty five million nine hundred fifty four thousand five hundred twenty three Three thousand ten

Six hundred sixty six nineteen million five hundred twenty seven thousand Thirty nine Two billion thirty thousand sixteen Three hundred forty one million nine hundred fifty four thousand eight hundred eighty eight nine thousand one Eight thousand three hundred ten twenty thousand fifty one 666 19 527 000 39 2 000 030 016 341 954 8888 9 001 8 310 20 051

Write these numbers in words, then try and say them outloud. a) b) c) d) e) f) g) h) i) j) 345 20 45 907 5 678 7 000 12 002 75 802 282 56 2 450 781 a) Three hundred forty five b) Twenty c) Forty Five thousand nine hundred seven d) Five thousand six hundred seventy eight e) Seven thousand f) Twelve thousand two g) Seventy five thousand eight hundred two h) Two hundred eighty two i) Fifty six j) Two million four hundred fifty thousand seven hundred eighty one

When writing a large number put a space between each period 345 905 - Canadian Way 345, 905 - American Way Sometimes you will see a larger numbe written with a comma in between the periods. This is the American way of writing larger numbers

Practice Can you say these large numbers out loud? a). 531 b). 1 256 c). 72 078 d). 450 943 e). 67 f). 72 078 g). 601 345 h). 3 567 980 i). 13 500 001

a). 531 b). 1 256 c). 72 078 d). 450 943 e). 67 f). 72 078 g). 601 345 Practice a). Five hundred thirty one b). One thousand two hundred fifty six c). Seventy two thousand seventy eight d). Four hundred fifty thousand nine hundred forty three e). Sixty seven f). Seventy two thousand seventy eight g). Six hundred one thousand three hundred forty five h). 3 567 980 h). Three million five hundred sixty seven thousand nine hundred eighty i). 13 500 001 h). Thirteen million five hundred one


Standard Form • When numbers are presented in numerical digits, it is called the standard form of a number. • a number is written using digits and place value (the regular way to write numbers). Standard Forms e. g. 4 856 67 1 78 900 679

Expanded Form • A number is written as a sum using the place and value of each digit. • This means writing, separately, the value of each digit in the each place value the number. • The values must be written from largest to smallest, and have an addition sign to shown they are combined • Zero values are not included.

Expanded Form The number 4856 in expanded form is: Method a) 4000 + 800 + 50 + 6 You may see expanded form written like this: Method b) 4 x 1000 + 8 x 100 + 5 x 10 + 6 x 1 Both methods are correct.

Expanded Form The number 5 062 in expanded form is: 5000 + 60 + 2 ** Because there is no value for the hundreds place, we can leave the value of the hundreds place out when writing the expanded form. 5 062 = 5000 + 60 + 2

A trick to writing number in standard form from expanded form is to show the number of lines as there is place values e. g. Write in standard form 50 000 + 6 000 + 700 + 2 50 000 is the largest of the expanded form shown. So we need Five place value lines ____ _____ The face value of the ten thousands place is 5. Put in 5. _5__ _____

(Continued) Write in standard form 50 000 + 6 000 + 700 + 2 The face value of the thousands place is 6. Put in 6. _5__ __6__ _____ The face value of the hundreds place is 7. Put in 7. _5__ __6__ __7__ _____ The face value of the tens place is 0, because there is no value for the tens place shown. Put in 0. _5__ __6__ __ 7 _ __0_ _____ The face value of the hundreds place is 2. Put in 2. _5__ __6__ __7__ __ 0 __ __2__

Practice Write the following number in standard form. 504 a) 500 + 4 672 b) 600 + 70 + 2 62 945 c) 60 000 + 2000 + 900 + 40 + 5 850 364 d) 800 000 + 50 000 + 300 + 60 + 4 e) 3 x 100 000 + 7 x 10 000 + 2 x 1000 372 845 + 8 x 100 + 4 x 10 + 5 x 1 602 800 f) 6 x 100 000 + 2 x 1000 + 8 x 100 g) 5 x 10 + 6 x 1 56

Practice Write the following number in expanded form. a) 500 + 60 + 8 a) 568 b) 10 + 2 b) 12 c) 50 000 + 8 000 + 900 c) 58 900 d) 123 091 d) 100 000 + 20 000 +3 000 + 90 + 1 e) 104 044 e) 100 000 + 40 + 4 f) 1 678 932 f) 1 000 + 600 000 + 70 000 g) 12 456 + 8 000 + 900 + 30 + 2 g) 10 000 + 2 000 + 400 + 50 + 6

Standard Form: is the number itself. e. g. 1; 15, 000; 367 Written Form: is the words for the numbers e. g. one; sixty; twelve million; two hundred eighty thousand ten. Expanded Form: is writing a number by separating it into each of its place values. Two Versions: a). 789 123 = (7 x 100 000) + (8 x 10 000) + (9 x 1 000) + (1 x 100) + (2 x 10) + (3 x 1) b) 789 123 = 700 000 + 80 000 + 9 000 + 100 + 20 + 3 Standard Form Expanded Form Written Form 10 589 (1 x 10 000) + (5 x 100) + (8 x 10) + (9 x 1) Ten thousand five hundred eighty nine 7 589 588 (7 x 1 000) + (5 x 100 000) + (8 x 10 000) + (9 x 1 000) + (5 x 100) + (8 x 1) Seven million five hundred eighty nine thousand five hundred eighty eight 12. 078 (1 x 10) + (2 x 1) + (7 x 0. 01) + (8 x 0. 001) Twelve AND seventy eight thousandths 0. 54669 (5 x 0. 1) + (4 x 0. 01) + (6 x 0. 0001) + (9 x 0. 00001) Fifty four thousand six hundred sixty nine hundred thousandths

Practice Write the following number in standard, expanded and written form. a) 234 b) 3 405 c) 561 783 d) 1 876 980

Practice Write the following number in standard, expanded and written form. a) 234 – 234 - 200 + 30 + 4 - two hundred thirty four b) 3 405 – 3 405 - 3000 + 400 + 5 - threee thousand four hundred five c) 561 783 – 561 783 - 500 000 + 60 000 + 1 000 + 700 + 80 + 3 - five hundred sixty one thousand seven hundred eighty three.

Practice d) 1 876 980 – 1 876 980 - 1 000 + 800 000 + 70 000 + 6 000 + 900 + 80 - one million eight hundred seventy six thousand nine hundred eighty

Representing Numbers How many ways can you think of to represent the value of a number? - Standard form (numbers) - Written form (words) - Expanded form (values) - Scientific Notation (values) - Money (values) Can you think of any other ways to show the value of a number?

What about …. .

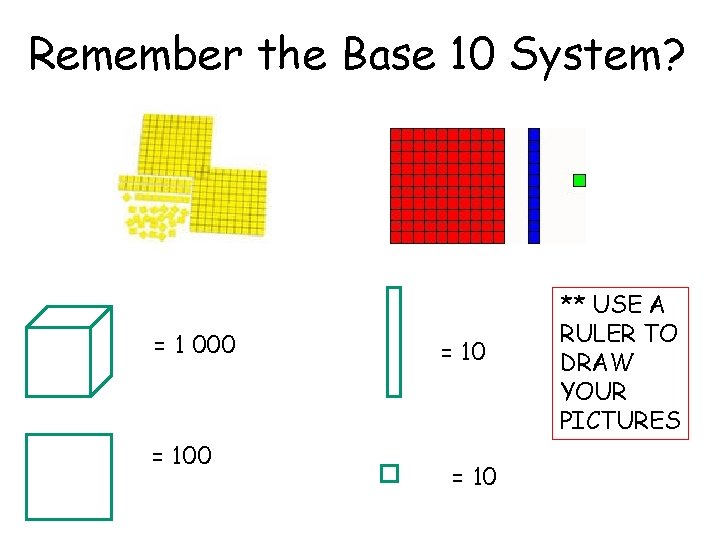
Remember the Base 10 System? = 1 000 = 10 ** USE A RULER TO DRAW YOUR PICTURES

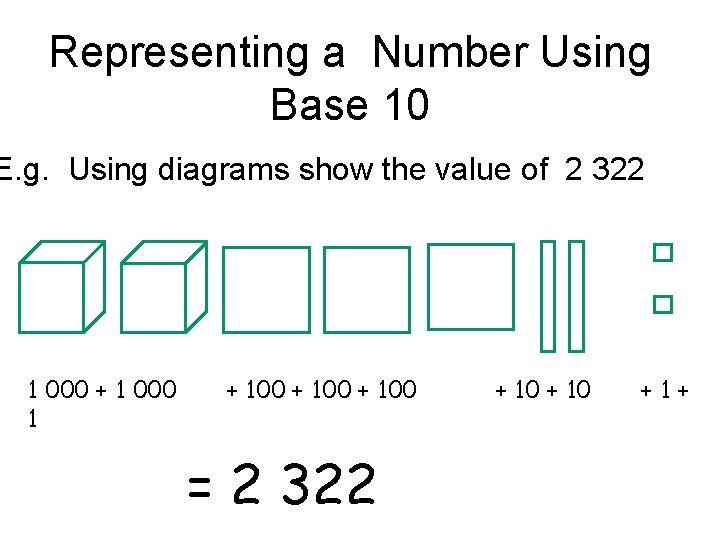
Representing a Number Using Base 10 E. g. Using diagrams show the value of 2 322 1 000 + 1 000 1 + 100 = 2 322 + 10 +1+

Practice Using the following pictures, write the following numbers in standard form. a) b) c) d) 1 111 425 332 3 150

Problem Using four different methods represent the value of the number 3 451. 1. Pictures 2. Expanded Form 3000 + 400 + 50 + 1 3. Written Form Three thousand four hundred fifty one 4. Scientific Notation 3 x 103 + 4 x 102 + 5 x 101 + 1 x 100